Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T13:06:47.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Tilting subcategories with respect to cotorsion triples in abelian categories

Part of: Commutative algebra: Homological methods Homological algebra

Published online by Cambridge University Press:  28 June 2017

Zhenxing Di ,
Jiaqun Wei ,
Xiaoxiang Zhang  and
Jianlong Chen
Zhenxing Di
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou 730070, People's Republic of China (dizhenxing19841111@126.com)
Jiaqun Wei
Affiliation:
Institute of Mathematics, School of Mathematical Sciences, Nanjing Normal University, Nanjing 210023, People's Republic of China (weijiaqun@njnu.enu.cn)
Xiaoxiang Zhang
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, People's Republic of China (z990303@seu.edu.cn; jlchen@seu.edu.cn)
Jianlong Chen
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, People's Republic of China (z990303@seu.edu.cn; jlchen@seu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Extract

Given a non-negative integer n and a complete hereditary cotorsion triple 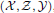, the notion of 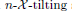subcategories in an abelian category 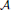is introduced. It is proved that a virtually Gorenstein ring R is n-Gorenstein if and only if the subcategory 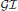of Gorenstein injective R-modules is 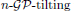with respect to the cotorsion triple 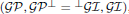, where 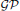stands for the subcategory of Gorenstein projectives. In the case when a subcategory 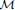of 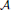is closed under direct summands such that each object in 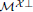admits a right 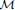-approximation, a Bazzoni characterization is given for 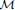to be 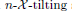. Finally, an Auslander–Reiten correspondence is established between the class of 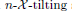subcategories and that of certain subcategories of 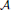which are 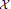-coresolving covariantly finite and closed under direct summands.

Keywords

cotorsion tripletilting subcategoryBazzoni's characterizationpartial orderAuslander–Reiten correspondence

MSC classification

Secondary: 13D05: Homological dimension 13D07: Homological functors on modules (Tor, Ext, etc.) 18G15: Ext and Tor, generalizations, Künneth formula 18G25: Relative homological algebra, projective classes
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 147 , Issue 4 , August 2017 , pp. 703 - 726
Copyright
Copyright © Royal Society of Edinburgh 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)