Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T10:54:06.012Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness and multiplicity of positive solutions for a diffusive predator–prey model in the heterogeneous environment

Part of: Partial differential equations

Published online by Cambridge University Press:  20 January 2020

Shanbing Li  and
Yaying Dong
Shanbing Li
Affiliation:
School of Mathematics and Statistics, Xidian University, Xi'an 710071, PR China
Yaying Dong
Affiliation:
School of Science, Xi'an Polytechnic University, Xi'an 710048, PR China (lishanbing@xidian.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

This is the second part of our study on the spatially heterogeneous predator–prey model where the interaction is governed by a Crowley–Martin type functional response. In part I, we have proved that when the predator competition is strong (i.e. k is large), the model has at most one positive steady-state solution for any 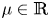$\mu \in \mathbb {R}$, moreover it is globally asymptotically stable for any 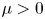$\mu >0$. This part is denoted to study the effect of saturation. Our result shows that the large saturation coefficient (i.e. large m) can not only lead to the uniqueness of positive solutions, but also lead to the multiplicity of positive solutions, moreover the stability of the corresponding positive solutions is also completely obtained. This work can be regarded as a supplement of Ref. [10].

Keywords

Predator–prey modelspatial heterogeneitysaturationuniquenessmultiplicity

MSC classification

Primary: 92D40: Ecology
Secondary: 35B30: Dependence of solutions on initial and boundary data, parameters 35B32: Bifurcation 92D25: Population dynamics (general)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 6 , December 2020 , pp. 3321 - 3348
Check for updates
Copyright
Copyright © The Author(s) 2020. Published by The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Crandall, M. G. and Rabinowitz, P. H.. Bifurcation from simple eigenvalues. J. Funct. Anal. 8 (1971), 321–340.CrossRefGoogle Scholar
2Cui, R. H., Shi, J. P. and Wu, B. Y.. Strong Allee effect in a diffusive predator-prey system with a protection zone. J. Differential Equations 256 (2014), 108–129.CrossRefGoogle Scholar
3Dancer, E. N.. Global solution branches for positive mappings. Arch. Rational Mech. Anal. 52 (1973), 181–192.CrossRefGoogle Scholar
4Dancer, E. N.. On the indices of fixed points of mappings in cones and applications. J. Math. Anal. Appl. 91 (1983), 131–151.CrossRefGoogle Scholar
5Dancer, E. N.. On positive solutions of some pairs of differential equations. Trans. Amer. Math. Soc. 284 (1984), 729–743.CrossRefGoogle Scholar
6Dancer, E. N.. On positive solutions of some pairs of differential equations, II. J. Differential Equations 60 (1985), 236–258.CrossRefGoogle Scholar
7Du, Y. H. and Liang, X.. A diffusive competition model with a protection zone. J. Differential Equations 244 (2008), 61–86.CrossRefGoogle Scholar
8Du, Y. H. and Lou, Y.. Some uniqueness and exact multiplicity results for a predator-prey model. Trans. Amer. Math. Soc. 349 (1997), 2443–2475.CrossRefGoogle Scholar
9Du, Y. H. and Shi, J. P.. A diffusive predator-prey model with a protection zone. J. Differential Equations 229 (2006), 63–91.CrossRefGoogle Scholar
10Du, Y. H., Peng, R. and Wang, M. X.. Effect of a protection zone in the diffusive Leslie predator-prey model. J. Differential Equations 246 (2009), 3932–3956.CrossRefGoogle Scholar
11He, X. and Zheng, S. N.. Protection zone in a diffusive predator-prey model with Beddington-DeAngelis functional response. J. Math. Biol. 75 (2017), 239–257.CrossRefGoogle Scholar
12Li, S. B. and Wu, J. H.. Effect of cross-diffusion in the diffusion prey-predator model with a protection zone. Discrete Contin. Dyn. Syst. 37 (2017), 1539–1558.CrossRefGoogle Scholar
13Li, S. B. and Yamada, Y.. Effect of cross-diffusion in the diffusion prey-predator model with a protection zone II. J. Math. Anal. Appl. 461 (2018), 971–992.CrossRefGoogle Scholar
14Li, S. B., Wu, J. H. and Liu, S. Y.. Effect of cross-diffusion on the stationary problem of a Leslie prey-predator model with a protection zone. Calc. Var. Partial Differential Equations 56 (2017), 82.CrossRefGoogle Scholar
15Li, S. B., Liu, S. Y., Wu, J. H. and Dong, Y. Y.. Positive solutions for Lotka-Volterra competition system with large cross-diffusion in a spatially heterogeneous environment. Nonlinear Anal. Real World Appl. 36 (2017), 1–19.Google Scholar
16Li, S. B., Wu, J. H. and Dong, Y. Y.. Uniqueness and stability of positive solutions for a diffusive predator-prey model in heterogeneous environment. Calc. Var. Partial Differential Equations 58 (2019), 110.CrossRefGoogle Scholar
17López-Gómez, J.. Spectral theory and nonlinear functional analysis, Research Notes in Mathematics, vol. 426 (Boca Raton, FL: CRC Press, 2001).CrossRefGoogle Scholar
18López-Gómez, J.. Linear second order elliptic operators (Singapore: World Scientific, 2013).CrossRefGoogle Scholar
19Oeda, K.. Effect of cross-diffusion on the stationary problem of a prey-predator model with a protection zone. J. Differential Equations 250 (2011), 3988–4009.CrossRefGoogle Scholar
20Rabinowitz, P. H.. Some global results for nonlinear eigenvalue problem. J. Funct. Anal. 7 (1971), 487–513.CrossRefGoogle Scholar
21Shi, J. P. and Wang, X. F.. On global bifurcation for quasilinear elliptic systems on bounded domains. J. Differential Equations 246 (2009), 2788–2812.CrossRefGoogle Scholar
22Wang, Y. X. and Li, W. T.. Effects of cross-diffusion on the stationary problem of a diffusive competition model with a protection zone. Nonlinear Anal. Real World Appl. 14 (2013), 224–245.CrossRefGoogle Scholar
23Ye, Q. X., Li, Z. Y., Wang, M. X. and Wu, Y. P.. Introduction to reaction-diffusion equations, 2nd ed. (Beijing: Science Press, 2011). (in Chinese).Google Scholar