No CrossRef data available.
Article contents
V.—On Whittaker's Solution of Laplace's Equation
Published online by Cambridge University Press: 14 February 2012
Extract
In 1902, Professor E. T. Whittaker gave a general solution of Laplace's equation in the form
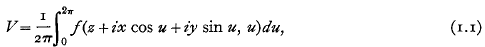
where f is an arbitrary function of the two variables. It appears that this is not the most general solution, since there are harmonic functions, such as r−1Q0(cos θ), which cannot be expressed in this form near the origin. The difficulty is naturally connected with the location of the singular points of the harmonic function. It seems therefore to be worth while considering afresh the conditions under which Whittaker's solution is valid.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 62 , Issue 1 , 1944 , pp. 31 - 36
- Copyright
- Copyright © Royal Society of Edinburgh 1944
References
* Math. Ann., LVII, 1902, 333. See also , Whittaker and , Watson, Modern Analysis (1920), 389–390.Google Scholar
† Bergman, S., Math. Zeits., xxiv, 1926, 641–669CrossRefGoogle Scholar seems to be the only writer who has considered at all the analytical character of Whittaker's solution, but his results are somewhat inaccurate and hardly deal with the point at issue here.
‡ We use in this section a number of well-known properties of harmonic functions which can all be found in , Goursat, Cours d'Analyse, III, 1923, ch. 28Google Scholar.


