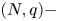 Laplacian equation in $\mathbb {R}^N$
Laplacian equation in $\mathbb {R}^N$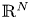 with new exponential growth conditions
with new exponential growth conditionsPublished online by Cambridge University Press: 07 September 2023
In this paper, we prove some weighted sharp inequalities of Trudinger–Moser type. The weights considered here have a logarithmic growth. These inequalities are completely new and are established in some new Sobolev spaces where the norm is a mixture of the norm of the gradient in two different Lebesgue spaces. This fact allowed us to prove a very interesting result of sharpness for the case of doubly exponential growth at infinity. Some improvements of these inequalities for the weakly convergent sequences are also proved using a version of the Concentration-Compactness principle of P.L. Lions. Taking profit of these inequalities, we treat in the last part of this work some elliptic quasilinear equation involving the weighted $(N,q)-$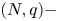 Laplacian operator where $1 < q < N$
Laplacian operator where $1 < q < N$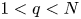 and a nonlinearities enjoying a new type of exponential growth condition at infinity.
and a nonlinearities enjoying a new type of exponential growth condition at infinity.