Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T03:08:02.504Z Has data issue: false hasContentIssue false
  • English
  • Français

Which special functions of bounded deformation have bounded variation?

Part of: Functions of several variables

Published online by Cambridge University Press:  17 October 2017

Sergio Conti ,
Matteo Focardi  and
Flaviana Iurlano
Sergio Conti
Affiliation:
Institut für Angewandte Mathematik, Universität Bonn, 53115 Bonn, Germany (sergio.conti@uni-bonn.de)
Matteo Focardi
Affiliation:
Dipartimento di Matematica e Informatica ‘Ulisse Dini’ (DiMaI), Università di Firenze, 50134 Firenze, Italy (focardi@math.unifi.it)
Flaviana Iurlano
Affiliation:
Institut für Angewandte Mathematik, Universität Bonn, 53115 Bonn, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

Functions of bounded deformation (BD) arise naturally in the study of fracture and damage in a geometrically linear context. They are related to functions of bounded variation (BV), but are less well understood. We discuss here the relation to BV under additional regularity assumptions, which may require the regular part of the strain to have higher integrability or the jump set to have finite area or the Cantor part to vanish. 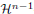On the positive side, we prove that BD functions that are piecewise affine on a Caccioppoli partition are in GSBV, and we prove that SBDp functions are approximately continuous -almost everywhere away from the jump set. On the negative side, we construct a function that is BD but not in BV and has distributional strain consisting only of a jump part, and one that has a distributional strain consisting of only a Cantor part.

Keywords

bounded deformationbounded variationCaccioppoli partitionapproximate continuity

MSC classification

Secondary: 26B30: Absolutely continuous functions, functions of bounded variation
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 1 , February 2018 , pp. 33 - 50
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)