Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-27T06:50:34.433Z Has data issue: false hasContentIssue false
  • English
  • Français

XVIII.—The Riemann Tensor in a Completely Harmonic V4

Published online by Cambridge University Press:  14 February 2012

H. S. Ruse
H. S. Ruse
Affiliation:
University College, Southampton
Get access Rights & Permissions [Opens in a new window]

Extract

If 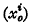is a fixed point of a Riemannian Vn of fundamental tensor gij, and if s is the geodesic distance between it and a variable point (xi), then the Vn has been called centrally harmonic with respect to the base-point 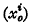if

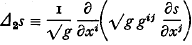
is a function of s only, and completely harmonic if this holds for every choice of base-point 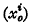. A flat Vn (gij=δij) is obviously completely harmonic, since for such a space 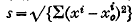and

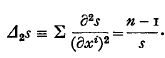
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 62 , Issue 2 , 1946 , pp. 156 - 163
Copyright
Copyright © Royal Society of Edinburgh 1946

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES TO LITERATURE

Bôcher, M., 1936. Introduction to higher algebra (Macmillan, New York).Google Scholar
Copson, E. T., and Ruse, H. S., 1940. “Harmonic Riemannian Spaces,” Proc. Roy. Soc. Edinburgh, LX, 117–133.CrossRefGoogle Scholar
Hudson, R. W. H. T., 1905. Kummer's quartic surface, Cambridge.Google Scholar
Jessop, C. M., 1903. A treatise on the line complex, Cambridge.Google Scholar
Ruse, H. S., 1930-1931. “On the ‘elementary’ solution of Laplace's equation,” Proc. Edinburgh Math. Soc. (2), 11, 135–139.CrossRefGoogle Scholar
Ruse, H. S., 1944. “On the line-geometry of the Riemann tensor,” Proc. Roy. Soc. Edinburgh, A, LXII, 64–73.Google Scholar
Ruse, H. S., 1945 a. “The five-dimensional geometry of the curvature tensor in a Riemannian V4,” Quarterly Journal of Math. (Oxford) (in press).Google Scholar
Ruse, H. S., 1945 b. “Sets of vectors in a V4 defined by the Riemann tensor,” Journal London Math. Soc. (in press).Google Scholar
Ruse, H. S., 1946 (?). “The self-polar Riemann complex for a V4,” Proc. London Math. Soc. (in press).Google Scholar
Sommerville, D. M. Y., 1934. Analytical geometry of three dimensions, Cambridge.Google Scholar
Walker, A. G., 1942. “Note on a distance invariant and the calculation of Ruse's invariant,” Proc. Edinburgh Math. Soc. (2), VII, 16–26.CrossRefGoogle Scholar
Zindler, K., 1922. “Algebraische Liniengeometrie,” Encyklopädie der Math. Wiss., III, C 8, 973–1228.Google Scholar