We consider a family of Caffarelli–Kohn–Nirenberg interpolation inequalities and weighted logarithmic Hardy inequalities that were obtained recently as a limit case of the Caffarelli–Kohn–Nirenberg inequalities. We discuss the ranges of the parameters for which the optimal constants are achieved by extremal functions. The comparison of these optimal constants with the optimal constants of Gagliardo–Nirenberg interpolation inequalities and Gross's logarithmic Sobolev inequality, both without weights, gives a general criterion for such an existence result in some particular cases.

We give characterizations of the positive Borel measures μ on so that the weighted Hardy–Sobolev spaces are imbedded in Lq(dμ), for a range of s > 0, 0 < p, q < + ∞, q ≠ p, where w is a doubling weight in the unit sphere of ℂn.

Let (M, g) be a compact smooth N-dimensional Riemannian manifold without boundary. We consider the multiple existence of positive solutions of the problem

where Δg stands for the Laplacian in M and f ε C2(M).

Let p ∈ (1, ∞) and let Ω ⊆ ℝN be a bounded domain with Lipschitz continuous boundary. We characterize on L2(Ω) all order-preserving semigroups that are generated by convex, lower semicontinuous, local functionals and are sandwiched between the semigroups generated by the p-Laplace operator with Dirichlet and Neumann boundary conditions. We show that every such semigroup is generated by the p-Laplace operator with Robin-type boundary conditions.

We investigate the properties of the global attractor of hyperbolic balance laws on the circle, given by

ut + f(u)x = g(u).

The new tool of sub-attractors is introduced. They contain all solutions on the global attractor up to a given number of zeros. The paper proves finite dimensionality of all sub-attractors, provides a full parametrization of all sub-attractors and derives a system of ordinary differential equations for the embedding parameters that describe the full partial differential equation dynamics on the sub-attractor.

We study the existence of positive solutions for the nonlinear Schrödinger equation with the fractional Laplacian

Furthermore, we analyse the regularity, decay and symmetry properties of these solutions.

We study the inhomogeneous semilinear parabolic equation

with source term f independent of time and subject to f(x) ≥ 0 and with u(0, x) = φ(x) ≥ 0, for the very general setting of a metric measure space. By establishing Harnack-type inequalities in time t and some powerful estimates, we give sufficient conditions for non-existence, local existence and global existence of weak solutions, depending on the value of p relative to a critical exponent.

We are interested in variational problems involving weights that are singular at a point of the boundary of the domain. More precisely, we study a linear variational problem related to the Poincaré inequality and to the Hardy inequality for maps in H01(Ω), where Ω is a bounded domain in ℝN, N ≥ 2, with 0 ∈ ∂Ω. In particular, we give sufficient and necessary conditions so that the best constant is achieved.

Let M be a closed 4-manifold with a free circle action. If the orbit manifold N3 satisfies an appropriate fibering condition, then we show how to represent a cone in H2(M; ℝ) by symplectic forms. This generalizes earlier constructions by Thurston, Bouyakoub and Fernández et al. In the case that M is the product 4-manifold S1 × N, our construction complements our previous results and allows us to determine completely the symplectic cone of such 4-manifolds.

We study the existence and multiplicity of positive solutions for the Dirichlet problem

where λ > 0, 1 < q < 2, p = 2* = 2N/(N − 2), 0 ε Ω ⊂ ℝN, N ≥ 3, is a bounded domain with smooth boundary ∂Ω and f is a non-negative continuous function on . Assuming that f satisfies some hypothesis, we prove that the equation admits at least three positive solutions for sufficiently small λ.

An adequate semigroup S is called ample if ea = a(ea)* and ae = (ae)†a for all a ∈ S and e ∈ E(S). Inverse semigroups are exactly those ample semigroups that are regular. After obtaining some characterizations of finite ample semigroups, it is proved that semigroup algebras of finite ample semigroups have generalized triangular matrix representations. As applications, the structure of the radicals of semigroup algebras of finite ample semigroups is obtained. In particular, it is determined when semigroup algebras of finite ample semigroup are semiprimitive.

We consider the T-periodic problem

where g: [0,T]×]0,+∞[→ℝ exhibits a singularity of a repulsive type at the origin, and an asymptotically linear behaviour at infinity. In particular, for large x, g(t, x) is controlled from both sides by two consecutive asymptotes of the T-periodic Fučik spectrum, with possible equality on one side. Using a suitable Landesman–Lazer-type condition, we prove the existence of a solution.

We combine the sub- and supersolution method and perturbation arguments to obtain positive solutions of singular quasi-monotone (p, q)-Laplacian systems.

We are concerned with the solvability of nonlinear second-order elliptic partial differential equations with nonlinear boundary conditions. We study the generalized Steklov–Robin eigenproblem (with possibly singular weights) in which the spectral parameter is both in the differential equation and on the boundary. We prove the existence of solutions for nonlinear problems when both nonlinearities in the differential equation and on the boundary interact, in some sense, with the generalized spectrum. The proofs are based on variational methods and a priori estimates.

We study the blow-up phenomenon for non-negative solutions to the following parabolic problem:

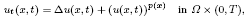
where 0 < p− = min p ≤ p(x) ≤ max p = p+ is a smooth bounded function. After discussing existence and uniqueness, we characterize the critical exponents for this problem. We prove that there are solutions with blow-up in finite time if and only if p+ > 1.

When Ω = ℝN we show that if p− > 1 + 2/N, then there are global non-trivial solutions, while if 1 < p− ≤ p+ ≤ 1 + 2/N, then all solutions to the problem blow up in finite time. Moreover, in the case when p− < 1 + 2/N < p+, there are functions p(x) such that all solutions blow up in finite time and functions p(x) such that the problem possesses global non-trivial solutions.

When Ω is a bounded domain we prove that there are functions p(x) and domains Ω such that all solutions to the problem blow up in finite time. On the other hand, if Ω is small enough, then the problem possesses global non-trivial solutions regardless of the size of p(x).

A theorem is proven for kth-order polynomial finite-difference equations that guarantees the divergence of solutions. A ‘basin of divergence’ is characterized and an order of divergence is provided. The basin of divergence is shown to depend on k independent parameters. An unconventional compactification method is used. Applications include the multi-step method in the numerical integration of ordinary differential equations, quadratic equations and the Henon map.

We provide new sufficient conditions for the existence of multiple fixed points for a map between ordered Banach spaces. An interesting feature of this approach is that we require conditions not on two boundaries, but rather on one boundary and a point with some extra information on the monotonicity of the nonlinearity on a certain set. We apply our results to prove the existence of at least two positive solutions for a nonlinear boundary-value problem that models a thermostat.

We consider the nonlinear elliptic equation driven by the p-Laplacian and with a Carathéodory reaction depending on a parameter λ > 0, looking for positive solutions. We prove two bifurcation-type results. In the first the bifurcation occurs near 0 (for small values of λ > 0) and our setting incorporates problems with the combined effects of concave and convex nonlinearities. In the second, the bifurcation occurs near +∞ (for large values of λ > 0) and our setting incorporates as a special case p-logistic equations with superdiffusive reaction. Our approach is variational, based on minimax methods and truncation techniques.

We investigate some properties of solutions of the Degasperis–Procesi equation, which is an approximation to the incompressible Euler equation in shallow water theory. Sufficient conditions for wave breaking are found both on an infinite line and in a periodic domain by the method of characteristics. Moreover, we show that the solution enjoys the same decay property as the initial data. Finally, the weak and strong limits, respectively, of the solution as the dispersive parameter goes to zero are investigated.

We study the motion of a rigid body with a cavity filled with a viscous liquid. The main objective is to investigate the well-posedness of the coupled system formed by the Navier–Stokes equations describing the motion of the fluid and the ordinary differential equations for the motion of the rigid part. To this end, appropriate function spaces and operators are introduced and analysed by considering a completely general three-dimensional bounded domain. We prove the existence of weak solutions using the Galerkin method. In particular, we show that if the initial velocity is orthogonal, in a certain sense, to all rigid velocities, then the velocity of the system decays exponentially to zero as time goes to infinity. Then, following a functional analytic approach inspired by Kato's scheme, we prove the existence and uniqueness of mild solutions. Finally, the functional analytic approach is extended to obtain the existence and uniqueness of strong solutions for regular data.