No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 15 September 2014
I. Term Representation of Diatomic Spectra.
The mathematical symbolism now employed by the practical spectroscopist for the representation of the energy term F(J) of the diatomic molecule has recently been fixed with precision as a result of the labours of Mulliken and others. The formula employed to represent the rotational term is
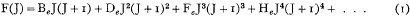
where J is the quantum number and Be, De, … are constants. BeJ(J + 1) is the kinetic energy, expressed in wave-numbers, which the molecule would have if it were a rigid rotator; and the remaining small correction terms in powers of J(J + 1) correspond to the expansion of the rotator under centrifugal force.
page 347 note * See Professor Richardson's, O. W. paper on “Nomenclature and Symbolism for the Spectra of Diatomic Molecules,” Trans. Faraday Soc., vol. xxv, 1929, p. 628.Google Scholar
page 347 note † E. Schrödinger, Collected Papers on Wave Mechanics, 1929, p. 34 et seq. Here the results are, however, not given in the form familiar to spectroscopists quoted in equation (1).
page 347 note ‡ Kratzer, A., Zeits. für Physik, vol. iii, 1920, p. 289; Phys. Zeits., vol. xxii, 1921, p. 552; and Ann. der Physik, vol. lxvii, 1922, p. 127.CrossRefGoogle Scholar
page 349 note * See “Molecular Spectra in Gases,” Bull. Nat. Res. Court., 1926, p. 237.
page 350 note * Proc. Roy. Soc., A, vol. cxxxi, 1931, p. 658.Google Scholar
page 351 note * Sandeman, I., Proc. Roy. Soc., A, vol. cxxxviii, 1932, p. 395.CrossRefGoogle Scholar
page 352 note * See Jevons's Report on Band-spectra of Diatomic Molecules, 1932, p. 29.
page 352 note † Proc. Roy. Soc., A, vol. cxxv, 1929, p. 23.Google Scholar
page 353 note * A. Kratzer, loc. cit.
page 353 note † Since the relation between the variables ρ and ξ in Kratzer's expression is ρ = ξ + I, substitution and expansion give
which is the same as the general expression above, and the same as the writer's expression, if b, c,… are neglected.
page 353 note ‡ This may be seen by substituting the writer's values of De, Fe, and He in the equations on p. 236 of Birge's article in the Report on Molecular Spectra in Gases, 1926, integrating Birge's force equation to obtain the equation of potential energy, and substituting the appropriate variable ξ=(r−re)/re.