Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T10:24:37.487Z Has data issue: false hasContentIssue false
  • English
  • Français

XXVI.—Plane Strain in a Wedge, with Applications to Masonry Dams

Published online by Cambridge University Press:  15 September 2014

S. D. Carothers
Get access

Extract

(1) It has been shown that in the case of plane strain the stresses in a body can be obtained from a single stress function χ satisfying

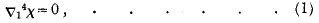
where

Solutions of equation (1) will be applied to obtain the stresses in an infinitely long wedge-shaped cylinder, having normal force varying according to some integral power of the distance from the angle applied to the plane faces, and the same at all corresponding points along the length of the cylinder.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 33 , 1914 , pp. 292 - 306
Copyright
Copyright © Royal Society of Edinburgh 1914

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 292 note * A. E. H. Love, Elasticity, 2nd edition, p. 201; or Michell, J. H., Proc. Lond. Math. Soc., vol. xxxi. p. 100.Google Scholar

page 293 note * Michell, J. H., Proc. Lond. Math. Soc., vol. xxxi. p. 111.Google Scholar

page 294 note * Force at an angle lias been treated by Professor J. H. Michell, Proc. Land. Math. Soc., vol. xxxiv. See also Love's Elasticity, p. 208.

page 296 note * For an equivalent solution by Professor Levy, see Comptes Rendus, vol. cxxvii. pp. 10–15, Paris, 1908.

page 301 note * Baldwin-Wiseman, Messrs and Griffith, , Proc. Inst. Civil Eng., vol. clxxix. p. 306.Google Scholar

page 304 note * For actual movements in the Vyrnwy dam, see Proc. Inst. Civil Eng., vol. cxv. p. 117.

page 304 note † Annales des ponts et chaussées, 1866, pp. 186, 212.

page 304 note ‡ Rankine's Miscellaneous Scientific Papers, p. 550.

page 304 note § Annales des ponts et chaussées, vol. x., 1875.

page 305 note * Some Disregarded Points in the Stability of Masonry Dams, London, 1904 (Dulau & Co.).

page 305 note † Proc. Inst. Civil Eng., vol. clxii. p. 120.

page 305 note ‡ ibid., p. 112.