Article contents
Identifiability of Hidden Markov Models for Learning Trajectories in Cognitive Diagnosis
Published online by Cambridge University Press: 01 January 2025
Abstract
Hidden Markov models (HMMs) have been applied in various domains, which makes the identifiability issue of HMMs popular among researchers. Classical identifiability conditions shown in previous studies are too strong for practical analysis. In this paper, we propose generic identifiability conditions for discrete time HMMs with finite state space. Also, recent studies about cognitive diagnosis models (CDMs) applied first-order HMMs to track changes in attributes related to learning. However, the application of CDMs requires a known Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varvec{Q}$$\end{document}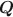 matrix to infer the underlying structure between latent attributes and items, and the identifiability constraints of the model parameters should also be specified. We propose generic identifiability constraints for our restricted HMM and then estimate the model parameters, including the Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varvec{Q}$$\end{document}
matrix to infer the underlying structure between latent attributes and items, and the identifiability constraints of the model parameters should also be specified. We propose generic identifiability constraints for our restricted HMM and then estimate the model parameters, including the Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varvec{Q}$$\end{document}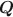 matrix, through a Bayesian framework. We present Monte Carlo simulation results to support our conclusion and apply the developed model to a real dataset.
matrix, through a Bayesian framework. We present Monte Carlo simulation results to support our conclusion and apply the developed model to a real dataset.
- Type
- Theory and Methods
- Information
- Copyright
- Copyright © 2023 The Author(s) under exclusive licence to The Psychometric Society.
References
- 3
- Cited by


