Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jin, Shaobo
Moustaki, Irini
and
Yang-Wallentin, Fan
2018.
Approximated Penalized Maximum Likelihood for Exploratory Factor Analysis: An Orthogonal Case.
Psychometrika,
Vol. 83,
Issue. 3,
p.
628.
Gu, Zhengguo
Schipper, Niek C. de
and
Van Deun, Katrijn
2019.
Variable Selection in the Regularized Simultaneous Component Analysis Method for Multi-Source Data Integration.
Scientific Reports,
Vol. 9,
Issue. 1,
Adachi, Kohei
2019.
Factor analysis: Latent variable, matrix decomposition, and constrained uniqueness formulations.
WIREs Computational Statistics,
Vol. 11,
Issue. 3,
Eldén, Lars
and
Trendafilov, Nickolay
2019.
Semi-sparse PCA.
Psychometrika,
Vol. 84,
Issue. 1,
p.
164.
Scharf, Florian
and
Nestler, Steffen
2019.
Should Regularization Replace Simple Structure Rotation in Exploratory Factor Analysis?.
Structural Equation Modeling: A Multidisciplinary Journal,
Vol. 26,
Issue. 4,
p.
576.
Carrizosa, Emilio
Guerrero, Vanesa
Romero Morales, Dolores
and
Satorra, Albert
2020.
Enhancing Interpretability in Factor Analysis by Means of Mathematical Optimization.
Multivariate Behavioral Research,
Vol. 55,
Issue. 5,
p.
748.
Xiang, Xiao
Wang, Siyue
Liu, Tianyi
Wang, Mengying
Li, Jiawen
Jiang, Jin
Wu, Tao
and
Hu, Yonghua
2020.
Exploring gene–gene interaction in family‐based data with an unsupervised machine learning method: EPISFA.
Genetic Epidemiology,
Vol. 44,
Issue. 8,
p.
811.
Huang, Po-Hsien
2020.
Postselection Inference in Structural Equation Modeling.
Multivariate Behavioral Research,
Vol. 55,
Issue. 3,
p.
344.
Chen, Jinsong
2021.
A Bayesian Regularized Approach to Exploratory Factor Analysis in One Step.
Structural Equation Modeling: A Multidisciplinary Journal,
Vol. 28,
Issue. 4,
p.
518.
de Schipper, Niek C.
and
Van Deun, Katrijn
2021.
Model selection techniques for sparse weight‐based principal component analysis.
Journal of Chemometrics,
Vol. 35,
Issue. 2,
Geminiani, Elena
Marra, Giampiero
and
Moustaki, Irini
2021.
Single- and Multiple-Group Penalized Factor Analysis: A Trust-Region Algorithm Approach with Integrated Automatic Multiple Tuning Parameter Selection.
Psychometrika,
Vol. 86,
Issue. 1,
p.
65.
Kim, Nam-Hwui
and
Browne, Ryan P.
2021.
In the pursuit of sparseness: A new rank-preserving penalty for a finite mixture of factor analyzers.
Computational Statistics & Data Analysis,
Vol. 160,
Issue. ,
p.
107244.
Perrot-Dockès, M.
Lévy-Leduc, C.
and
Rajjou, L.
2022.
Estimation of Large Block Structured Covariance Matrices: Application to ‘Multi-Omic’ Approaches to Study Seed Quality.
Journal of the Royal Statistical Society Series C: Applied Statistics,
Vol. 71,
Issue. 1,
p.
119.
Bergner, Yoav
Halpin, Peter
and
Vie, Jill-Jênn
2022.
Multidimensional Item Response Theory in the Style of Collaborative Filtering.
Psychometrika,
Vol. 87,
Issue. 1,
p.
266.
Chen, Jinsong
2022.
Fully and partially exploratory factor analysis with bi-level Bayesian regularization.
Behavior Research Methods,
Vol. 55,
Issue. 4,
p.
2125.
van Erp, Sara
2023.
Bayesian Regularized SEM: Current Capabilities and Constraints.
Psych,
Vol. 5,
Issue. 3,
p.
814.
Hirose, Kei
and
Terada, Yoshikazu
2023.
Sparse and Simple Structure Estimation via Prenet Penalization.
Psychometrika,
Vol. 88,
Issue. 4,
p.
1381.
Liu, Ruiping
Niang, Ndeye
Saporta, Gilbert
and
Wang, Huiwen
2023.
Sparse correspondence analysis for large contingency tables.
Advances in Data Analysis and Classification,
Vol. 17,
Issue. 4,
p.
1037.
Guo, Guangbao
Wei, Chunjie
and
Qian, Guoqi
2023.
Sparse online principal component analysis for parameter estimation in factor model.
Computational Statistics,
Vol. 38,
Issue. 2,
p.
1095.
Yamashita, Naoto
2024.
Exploratory Procedure for Component-Based Structural Equation Modeling for Simple Structure by Simultaneous Rotation.
Psychometrika,
Vol. 89,
Issue. 2,
p.
411.
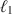 -norm penalties into the standard factor analysis problems. As a result, we propose sparse versions of the major factor analysis procedures. We illustrate the developed algorithms on well-known psychometric problems. Our sparse solutions are critically compared to ones obtained by other existing methods.
-norm penalties into the standard factor analysis problems. As a result, we propose sparse versions of the major factor analysis procedures. We illustrate the developed algorithms on well-known psychometric problems. Our sparse solutions are critically compared to ones obtained by other existing methods.
