Article contents
An Extended GFfit Statistic Defined on Orthogonal Components of Pearson’s Chi-Square
Published online by Cambridge University Press: 01 January 2025
Abstract
The Pearson and likelihood ratio statistics are commonly used to test goodness of fit for models applied to data from a multinomial distribution. The goodness-of-fit test based on Pearson’s Chi-squared statistic is sometimes considered to be a global test that gives little guidance to the source of poor fit when the null hypothesis is rejected, and it has also been recognized that the global test can often be outperformed in terms of power by focused or directional tests. For the cross-classification of a large number of manifest variables, the GFfit statistic focused on second-order marginals for variable pairs i, j has been proposed as a diagnostic to aid in finding the source of lack of fit after the model has been rejected based on a more global test. When data are from a table formed by the cross-classification of a large number of variables, the common global statistics may also have low power and inaccurate Type I error level due to sparseness in the cells of the table. The sparseness problem is rarely encountered with the GFfit statistic because it is focused on the lower-order marginals. In this paper, a new and extended version of the GFfit statistic is proposed by decomposing the Pearson statistic from the full table into orthogonal components defined on marginal distributions and then defining the new version, GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}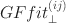 , as a partial sum of these orthogonal components. While the emphasis is on lower-order marginals, the new version of GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}
, as a partial sum of these orthogonal components. While the emphasis is on lower-order marginals, the new version of GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}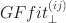 is also extended to higher-order tables so that the GFfit⊥\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }$$\end{document}
is also extended to higher-order tables so that the GFfit⊥\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }$$\end{document}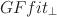 statistics sum to the Pearson statistic. As orthogonal components of the Pearson X2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$X^2$$\end{document}
statistics sum to the Pearson statistic. As orthogonal components of the Pearson X2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$X^2$$\end{document}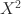 statistic, GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}
statistic, GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}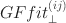 statistics have advantages over other lack-of-fit diagnostics that are currently available for cross-classified tables: the GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}
statistics have advantages over other lack-of-fit diagnostics that are currently available for cross-classified tables: the GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}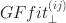 generally have higher power to detect lack of fit while maintaining good Type I error control even if the joint frequencies are very sparse, as will be shown in simulation results; theoretical results will establish that GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}
generally have higher power to detect lack of fit while maintaining good Type I error control even if the joint frequencies are very sparse, as will be shown in simulation results; theoretical results will establish that GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}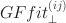 statistics have known degrees of freedom and are asymptotically independent with known joint distribution, a property which facilitates less conservative control of false discovery rate (FDR) or familywise error rate (FWER) in a high-dimensional table which would produce a large number of bivariate lack-of-fit diagnostics. Computation of GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}
statistics have known degrees of freedom and are asymptotically independent with known joint distribution, a property which facilitates less conservative control of false discovery rate (FDR) or familywise error rate (FWER) in a high-dimensional table which would produce a large number of bivariate lack-of-fit diagnostics. Computation of GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}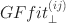 statistics is also computationally stable. The extended GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}
statistics is also computationally stable. The extended GFfit⊥(ij)\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$GFfit_{\perp }^{(ij)}$$\end{document}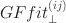 statistic can be applied to a variety of models for cross-classified tables. An application of the new GFfit statistic as a diagnostic for a latent variable model is presented.
statistic can be applied to a variety of models for cross-classified tables. An application of the new GFfit statistic as a diagnostic for a latent variable model is presented.
Keywords
- Type
- Theory and Methods
- Information
- Copyright
- Copyright © 2022 The Author(s) under exclusive licence to The Psychometric Society
Footnotes
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/s11336-022-09866-6.
References
- 2
- Cited by


