Hostname: page-component-5f745c7db-q8b2h Total loading time: 0 Render date: 2025-01-06T06:42:29.654Z Has data issue: true hasContentIssue false
  • English
  • Français

An Optimal Property of Least Squares Weights in Prediction Models

Published online by Cambridge University Press:  01 January 2025

Alan L. Gross
Alan L. Gross*
Affiliation:
The City University of New York
*
Requests for reprints should be sent to Alan L. Gross, Graduate Center, City University of New York, Ph.D. Program in Educational Psychology, New York, N.Y. 10036.
Get access Rights & Permissions [Opens in a new window]

Abstract

In predicting\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde y$$\end{document}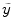 scores from p > 1 observed scores\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$(\tilde x)$$\end{document} in a sample of size ñ, the optimal strategy (minimum expected loss), under certain assumptions, is shown to be based upon the least squares regression weights\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$(\hat \beta )$$\end{document}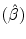 computed from a previous sample. Letting\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde r(\hat \beta )$$\end{document} represent the correlation between\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde y$$\end{document}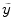 and the predicted values\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$(\hat \beta '\tilde x)$$\end{document}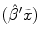, and letting\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde r(w)$$\end{document} 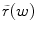represent the correlation between\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde y$$\end{document} 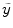and a different set of predicted values\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$(w'\tilde x)$$\end{document}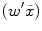, where w is any weighting system which is not a function of\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde y$$\end{document}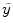, it is shown that the probability of\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde r(\hat \beta )$$\end{document} 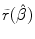being less than\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\tilde r(w)$$\end{document} 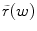cannot exceed .50. The relationship of this result to previous research and practical implications are discussed.

Keywords

least squares weightspredictioncross validitynoninformative prior distribution
Type
Original Paper
Information
Psychometrika , Volume 46 , Issue 2 , June 1981 , pp. 161 - 169
Copyright
Copyright © 1981 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Reference Note

Browne, M. W. Precision of prediction, 1969, Princeton, W.J.: Educational Testing Service.Google Scholar

References

Browne, M. W. Predictive validity of a linear regression equation. British Journal of Mathematical and Statistical Psychology, 1975, 28, 79–87.CrossRefGoogle Scholar
Darlington, R. B. Reduced variance regression. Psychological Bulletin, 1978, 85, 1238–1255.CrossRefGoogle ScholarPubMed
DeGroot, M. H. Optimal Statistical Decisions, 1970, New York: McGraw-Hill.Google Scholar
Dempster, A. P., Schatzoff, M. & Wermuth, N. A. A simulation study of alternatives to ordinary least squares. Journal of the American Statistical Association, 1977, 72, 77–91.CrossRefGoogle Scholar
Hoerl, A. E., & Kennard, R. W. Ridge regression: Biased estimation for non-orthogonal problems. Technometrics, 1970, 12, 55–63.CrossRefGoogle Scholar
James, W. & Stein, C. Estimation with quadratic loss. In Neyman, J. (Eds.), Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, 1961, Berkeley: The University of California Press.Google Scholar
Laughlin, J. E. A Bayesian alternative to least squares and equal weighting coefficients in regression. Psychometrika, 1979, 44, 271–288.CrossRefGoogle Scholar
Lindley, D. V. & Smith, A. F. M. Bayes estimates for the linear model. Journal of the Royal Statistical Society, Series B, 1972, 34, 1–41.CrossRefGoogle Scholar
Marquardt, D. W. & Snee, R. D. Ridge regression in practice. The American Statistican, 1975, 29, 3–20.CrossRefGoogle Scholar
Novick, M. R. & Jackson, P. H. Statistical Methods for Educational and Psychological Research, 1974, New York: McGraw-Hill.Google Scholar
Press, S. J. Applied Multivariate Analysis, 1972, New York: Holt, Rinehart & Winston.Google Scholar
Schmidt, F. L. The relative efficiency of regression and simple unit predictor weights in applied differential psychology. Educational and Psychological Measurement, 1971, 31, 699–714.CrossRefGoogle Scholar
Smith, G. & Campbell, F. A critique of some ridge regression methods. Journal of the American Statistical Association, 1980, 75, 74–81.CrossRefGoogle Scholar
Sclove, S. Improved estimators for coefficients in linear regression. Journal of the American Statistical Association, 1968, 63, 596–606.CrossRefGoogle Scholar
Van Nostrand, R. C. Comment. Journal of the American Statistical Association, 1980, 75, 92–93.CrossRefGoogle Scholar
Wainer, H. Estimating coefficients in linear models: It don't make no nevermind. Psychological Bulletin, 1976, 83, 213–217.CrossRefGoogle Scholar
Wainer, H. & Thissen, D. Three steps toward robust regression. Psychometrika, 1976, 41, 9–34.CrossRefGoogle Scholar
Zellner, A. & Chetty, V. K. Prediction and decision problems in regression from the Bayesian point of view. Journal of the American Statistical Association, 1965, 60, 608–616.CrossRefGoogle Scholar