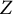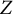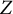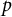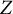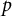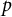1 Introduction
In this paper, we develop new statistics for confirmatory tests of unidimensionality based on the nonparametric item response theory (IRT) model of monotone homogeneity (MH) (Mokken, Reference Mokken1971) with binary items. This model assumes that there is a unidimensional (i.e., real-valued) variable
![]() $\Theta$
such that the items are conditionally independent given
$\Theta$
such that the items are conditionally independent given
![]() $\Theta$
, and such that the item regressions on
$\Theta$
, and such that the item regressions on
![]() $\Theta$
are monotone increasing. Many parametric IRT models, such as the 2PL model and the Rasch model, are a special case of MH. We develop our statistical tests for the context where researchers have the theory or hypothesis that items of a certain specified set or category all have a monotone regression on the same latent variable, while the specific shape of the regressions is unspecified; that is, it does not have to be logistic, as in the 2PL or the Rasch model, or any other function, such as the normal ogive. We assume that the objective of the test is to falsify the theory of unidimensionality. Thus, the objective is entirely aimed at fundamental theory development and not at the more pragmatic goal of building an efficient measurement tool.
$\Theta$
are monotone increasing. Many parametric IRT models, such as the 2PL model and the Rasch model, are a special case of MH. We develop our statistical tests for the context where researchers have the theory or hypothesis that items of a certain specified set or category all have a monotone regression on the same latent variable, while the specific shape of the regressions is unspecified; that is, it does not have to be logistic, as in the 2PL or the Rasch model, or any other function, such as the normal ogive. We assume that the objective of the test is to falsify the theory of unidimensionality. Thus, the objective is entirely aimed at fundamental theory development and not at the more pragmatic goal of building an efficient measurement tool.
Our objective of fundamental theory development rules out the possibility of assessing dimensionality with flexible parametric models such as latent class models (Douglas & Cohen, Reference Douglas and Cohen2001; Van Onna, Reference Van Onna2002; Vermunt, Reference Vermunt2001) or monotone polynomial models (Falk & Cai, Reference Falk and Cai2016). If such a parametric model is violated, it does not provide a convincing falsification of the theory because the violation may be caused by failure of the specific parametric assumptions. Conversely, if such a restrictive parametric model is not rejected, one may wonder whether maybe the statistical test used was not sensitive to some assumptions (e.g., van den Wollenberg, Reference Van den Wollenberg1982).
The new test statistics will be based on the recently developed Conditioning on Added Regression Predictions (CARP) statistics of Ellis and Sijtsma (Reference Ellis and Sijtsma2023). The CARP testing approach is a generalization of Rosenbaum’s (Reference Rosenbaum1984) case 5, in which one tests nonnegativity of the covariance of an item pair, conditionally on decile groups defined by the sum score on the other items. The generalization Ellis and Sijtsma proposed using a weighted sum score instead of a simple sum score, where the weights are based on regression analysis in a training sample. Ellis and Sijtsma (Reference Ellis and Sijtsma2023) argued that this is currently the only known partial test of conditional association (see next section) that can detect multidimensionality within monotone IRT models. This is the reason why we focus on this test statistic.
An important limitation of the CARP test is that it pertains to a single item pair. Generally, a test has many item pairs, and it would seem logical to apply a test to each item pair, but hitherto it has not been studied how such pairwise tests can be compounded into a single test statistic. The same is true for Rosenbaum’s case 5 test. For example, if a psychological test consists of 10 items, the CARP tests would yield 45
![]() $p$
-values, one for each item pair. The main question of this article is: How can the pairwise CARP statistics be aggregated into a single omnibus test?
$p$
-values, one for each item pair. The main question of this article is: How can the pairwise CARP statistics be aggregated into a single omnibus test?
The next section provides some background information about the CARP tests. After the specification of the hypothesis and the relevant pairwise statistics (mean conditional covariances (MCCs) and their
![]() $Z$
-values), we consider various methods to estimate the covariance matrix of the pairwise statistics. These estimated matrices are used in the theory of order restricted statistical inference (Robertson et al., Reference Robertson, Wright and Dykstra1988) and multiple testing (Davidov, Reference Davidov2011; Ellis et al., Reference Ellis, Pecanka and Goeman2018) to compound them into overall statistics in 20 different ways. We will compare the mathematical structure of some of these aggregated statistics to the most prominent competitor, which is the DETECT index (Zhang & Stout, Reference Zhang and Stout1999a, Reference Zhang and Stout1999b). Next, we use Monte Carlo simulations to study the Type 1 error rates and power of the ensuing tests and select the best tests.
$Z$
-values), we consider various methods to estimate the covariance matrix of the pairwise statistics. These estimated matrices are used in the theory of order restricted statistical inference (Robertson et al., Reference Robertson, Wright and Dykstra1988) and multiple testing (Davidov, Reference Davidov2011; Ellis et al., Reference Ellis, Pecanka and Goeman2018) to compound them into overall statistics in 20 different ways. We will compare the mathematical structure of some of these aggregated statistics to the most prominent competitor, which is the DETECT index (Zhang & Stout, Reference Zhang and Stout1999a, Reference Zhang and Stout1999b). Next, we use Monte Carlo simulations to study the Type 1 error rates and power of the ensuing tests and select the best tests.
2 Conditional association and CARP tests
Rosenbaum (Reference Rosenbaum1984) showed that MH implies that the item score variables have the property of conditional association, which means that any two increasing functions of any subtest have a nonnegative covariance conditionally upon any function of the items that were not included in the subtest. Holland and Rosenbaum (Reference Holland and Rosenbaum1986) generalized this result to non-binary items. Clarke and Yuan (Reference Clarke and Yuan2001) and De Gooijer and Yuan (Reference De Gooijer and Yuan2011) developed statistical tests for conditional association, but it is well known that a full test of conditional association is not feasible for realistic sizes of item sets because of the large number of tested conditions and the sparseness of the relevant response patterns. Several authors have therefore focussed on what Ligtvoet (Reference Ligtvoet2022) recently called “partial tests of conditional association.” These tests include MTP2 (Bartolucci & Forcina, Reference Bartolucci and Forcina2000; Ellis, Reference Ellis, Millsap, Bolt, van der Ark and Wang2015), nonnegative partial correlations (Ellis, Reference Ellis2014), nonnegative correlations (Mokken, Reference Mokken1971), and increasing item-rest regressions (“manifest monotonicity”; Junker & Sijtsma, Reference Junker and Sijtsma2000). Ellis and Sijtsma (Reference Ellis and Sijtsma2023) showed that all these conditions are insensitive to violations of unidimensionality if the data are generated by multiple latent variables that are independent or MTP2. They developed the CARP test, which includes Rosenbaum’s case 5 as a special case. This is currently the only known partial test of conditional association that can detect such violations. That is the reason why we focus on the CARP test.
3 Definitions
3.1 Definitions of variables
Assume that the item scores are binary manifest variables. Let variable
![]() ${X}_i$
represent the scores (1 = positive, 0 = negative) a random subject obtained on the
${X}_i$
represent the scores (1 = positive, 0 = negative) a random subject obtained on the
![]() $i$
-th item, and denote the full vector of item scores as
$i$
-th item, and denote the full vector of item scores as
![]() $\boldsymbol{X}=\left({X}_1,\dots, {X}_J\right)$
. For each item pair
$\boldsymbol{X}=\left({X}_1,\dots, {X}_J\right)$
. For each item pair
![]() $\left(i,j\right)$
, we assume that there is a discrete variable
$\left(i,j\right)$
, we assume that there is a discrete variable
![]() ${R}_{ij}$
that is used for creating groups in which the conditional covariances are computed. We call the
${R}_{ij}$
that is used for creating groups in which the conditional covariances are computed. We call the
![]() ${R}_{ij}$
s the conditioning variables, and we assume that they attain integer values ranging from 1 to
${R}_{ij}$
s the conditioning variables, and we assume that they attain integer values ranging from 1 to
![]() $\max {R}_{ij}$
. For example, in Case 2 of Rosenbaum (Reference Rosenbaum1984),
$\max {R}_{ij}$
. For example, in Case 2 of Rosenbaum (Reference Rosenbaum1984),
![]() ${R}_{ij}$
is defined as the sum score on the other items; that is, the items
${R}_{ij}$
is defined as the sum score on the other items; that is, the items
![]() ${X}_k$
with
${X}_k$
with
![]() $k\ne i,j$
. Then, we have
$k\ne i,j$
. Then, we have
![]() ${R}_{ij}=\left(\sum_{k=1}^J{X}_k\right)-{X}_i-{X}_j$
; we call this the pairwise rest score. In Case 5 of Rosenbaum (Reference Rosenbaum1984),
${R}_{ij}=\left(\sum_{k=1}^J{X}_k\right)-{X}_i-{X}_j$
; we call this the pairwise rest score. In Case 5 of Rosenbaum (Reference Rosenbaum1984),
![]() ${R}_{ij}$
consists of deciles of the pairwise rest score. In the CARP test of Ellis and Sijtsma (Reference Ellis and Sijtsma2023),
${R}_{ij}$
consists of deciles of the pairwise rest score. In the CARP test of Ellis and Sijtsma (Reference Ellis and Sijtsma2023),
![]() ${R}_{ij}$
consists of deciles of a weighted sum score on the other items, with weights estimated from a training sample. Let
${R}_{ij}$
consists of deciles of a weighted sum score on the other items, with weights estimated from a training sample. Let
![]() $\boldsymbol{R}$
be the vector of all
$\boldsymbol{R}$
be the vector of all
![]() ${R}_{ij}\;\left(i,j=1,\dots, J;i\ne j\right)$
.
${R}_{ij}\;\left(i,j=1,\dots, J;i\ne j\right)$
.
3.2 The hypothesis
The null hypothesis of interest is
However, the version of the Mantel–Haenszel statistic Rosenbaum (Reference Rosenbaum1984) and Ellis and Sijtsma (Reference Ellis and Sijtsma2023) used for testing
![]() ${\mathrm{H}}_0$
is rather based on a weighted mean of sample covariances, and it would be more precise to say that the null hypothesis is
${\mathrm{H}}_0$
is rather based on a weighted mean of sample covariances, and it would be more precise to say that the null hypothesis is
 $$\begin{align*}{\mathrm{H}}_0:\sum \limits_{s=1}^{\max {R}_{ij}}P\left({R}_{ij}=s\right) Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)\ge 0\;\mathrm{for}\;\mathrm{all}\;i,j=1,\dots, J.\end{align*}$$
$$\begin{align*}{\mathrm{H}}_0:\sum \limits_{s=1}^{\max {R}_{ij}}P\left({R}_{ij}=s\right) Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)\ge 0\;\mathrm{for}\;\mathrm{all}\;i,j=1,\dots, J.\end{align*}$$
3.3 Definition of the pairwise statistics
In this section, we define two sample statistics per item pair
![]() $\left(i,j\right)$
that we aggregate later. First, we define the mean of conditional covariances that estimates the quantity
$\left(i,j\right)$
that we aggregate later. First, we define the mean of conditional covariances that estimates the quantity
![]() $P\left({R}_{ij}=s\right) Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)$
in the null hypothesis. Second, we define the Z-statistic, which is the standardized version of the first statistic. The formal definition is the following.
$P\left({R}_{ij}=s\right) Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)$
in the null hypothesis. Second, we define the Z-statistic, which is the standardized version of the first statistic. The formal definition is the following.
Assume that there are
![]() $N$
i.i.d. copies of
$N$
i.i.d. copies of
![]() $\boldsymbol{X}$
, denoted by
$\boldsymbol{X}$
, denoted by
![]() ${\boldsymbol{X}}^{(n)}=\left({X}_1^{(n)},\dots, {X}_J^{(n)}\right)$
;
${\boldsymbol{X}}^{(n)}=\left({X}_1^{(n)},\dots, {X}_J^{(n)}\right)$
;
![]() $n=1,2,\dots, N$
.
$n=1,2,\dots, N$
.
![]() ${\boldsymbol{X}}^{(n)}$
contains the scores of the
${\boldsymbol{X}}^{(n)}$
contains the scores of the
![]() $n$
th subject in the sample. Let
$n$
th subject in the sample. Let
![]() ${I}_{ij s}^{(n)}:= 1\left[{R}_{ij}^{(n)}=s\right]$
denote the indicator function for the event
${I}_{ij s}^{(n)}:= 1\left[{R}_{ij}^{(n)}=s\right]$
denote the indicator function for the event
![]() ${R}_{ij}=s$
in subject
${R}_{ij}=s$
in subject
![]() $n$
. That is,
$n$
. That is,
![]() $1\left[{R}_{ij}^{(n)}=s\right]=1$
if
$1\left[{R}_{ij}^{(n)}=s\right]=1$
if
![]() ${R}_{ij}^{(n)}=s$
, and
${R}_{ij}^{(n)}=s$
, and
![]() $1\left[{R}_{ij}^{(n)}=s\right]=0$
otherwise. Let
$1\left[{R}_{ij}^{(n)}=s\right]=0$
otherwise. Let
![]() ${N}_{ijs}=\sum_{n=1}^N{I}_{ijs}^{(n)}$
denote the number of subjects with
${N}_{ijs}=\sum_{n=1}^N{I}_{ijs}^{(n)}$
denote the number of subjects with
![]() ${R}_{ij}^{(n)}=s$
. The conditional covariance in the subgroup with
${R}_{ij}^{(n)}=s$
. The conditional covariance in the subgroup with
![]() ${R}_{ij}^{(n)}=s$
is given by
${R}_{ij}^{(n)}=s$
is given by
 $$\begin{align*}{C}_{ijs}=\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}.\end{align*}$$
$$\begin{align*}{C}_{ijs}=\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}.\end{align*}$$
The version of the Mantel–Haenszel statistic Rosenbaum (Reference Rosenbaum1984) used is based on standardization of
 $$\begin{align*}{C}_{ij+}=\sum \limits_{s=1}^S{N}_{ij s}{C}_{ij s}.\end{align*}$$
$$\begin{align*}{C}_{ij+}=\sum \limits_{s=1}^S{N}_{ij s}{C}_{ij s}.\end{align*}$$
We refer to
![]() ${C}_{ij+}$
as the MCC. The standardization Rosenbaum used is based on the variance estimate
${C}_{ij+}$
as the MCC. The standardization Rosenbaum used is based on the variance estimate
 $$\begin{align*}{V}_{ij}=\sum \limits_{s=1}^S\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ij s}^{(n)}\sum \limits_{n=1}^N\left(1-{X}_i^{(n)}\right){I}_{ij s}^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ij s}^{(n)}\sum \limits_{n=1}^N\left(1-{X}_j^{(n)}\right){I}_{ij s}^{(n)}}{N_{ij s}^2\left({N}_{ij s}-1\right)}.\end{align*}$$
$$\begin{align*}{V}_{ij}=\sum \limits_{s=1}^S\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ij s}^{(n)}\sum \limits_{n=1}^N\left(1-{X}_i^{(n)}\right){I}_{ij s}^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ij s}^{(n)}\sum \limits_{n=1}^N\left(1-{X}_j^{(n)}\right){I}_{ij s}^{(n)}}{N_{ij s}^2\left({N}_{ij s}-1\right)}.\end{align*}$$
The Z-statistic is then defined as
 $$\begin{align*}{Z}_{ij}=\frac{C_{ij+}+0.5}{\sqrt{V_{ij}}}.\end{align*}$$
$$\begin{align*}{Z}_{ij}=\frac{C_{ij+}+0.5}{\sqrt{V_{ij}}}.\end{align*}$$
The term 0.5 is a continuity correction.
4 Estimation of the covariance matrix of the pairwise test statistics
In this section, we discuss the estimation of the covariance matrix of the
![]() ${C}_{ij+}$
s and the covariance matrix of the
${C}_{ij+}$
s and the covariance matrix of the
![]() ${Z}_{ij}$
s. These covariance matrices are conceptually like the asymptotic covariance matrices in structural equation modelling (SEM) because they estimate the covariance across all possible samples. However, because the asymptotic covariance matrices in SEM are typically derived from the model and typically pertain to model estimates rather than conditional covariances, we further refrain from focusing on the apparent similarity. Next, we delineate three estimation methods.
${Z}_{ij}$
s. These covariance matrices are conceptually like the asymptotic covariance matrices in structural equation modelling (SEM) because they estimate the covariance across all possible samples. However, because the asymptotic covariance matrices in SEM are typically derived from the model and typically pertain to model estimates rather than conditional covariances, we further refrain from focusing on the apparent similarity. Next, we delineate three estimation methods.
4.1 Estimation based on sample moments
The equation for MCC contains only sums of products and products of sums, divided by the
![]() ${N}_{ijs}$
. We worked out a formula for
${N}_{ijs}$
. We worked out a formula for
![]() $Cov\left({C}_{ijs},{C}_{klt}\right)$
, assuming that
$Cov\left({C}_{ijs},{C}_{klt}\right)$
, assuming that
![]() ${N}_{ijs}$
and
${N}_{ijs}$
and
![]() ${N}_{klt}$
are fixed values rather than random variables (see Appendix). This new equation uses only moments of the variables
${N}_{klt}$
are fixed values rather than random variables (see Appendix). This new equation uses only moments of the variables
![]() ${X}_i^{(n)}{I}_{ijs}^{(n)}$
,
${X}_i^{(n)}{I}_{ijs}^{(n)}$
,
![]() ${X}_j^{(n)}{I}_{ijs}^{(n)}$
,
${X}_j^{(n)}{I}_{ijs}^{(n)}$
,
![]() ${X}_k^{(n)}{I}_{klt}^{(n)}$
,
${X}_k^{(n)}{I}_{klt}^{(n)}$
,
![]() ${X}_l^{(n)}{I}_{klt}^{(n)}$
, and their products. By substituting the corresponding sample moments, one obtains an estimate
${X}_l^{(n)}{I}_{klt}^{(n)}$
, and their products. By substituting the corresponding sample moments, one obtains an estimate
![]() $\widehat{Cov}\left({C}_{ijs},{C}_{klt}\right)$
for
$\widehat{Cov}\left({C}_{ijs},{C}_{klt}\right)$
for
![]() $Cov\left({C}_{ijs},{C}_{klt}\right)$
. Next, the required covariance is estimated as
$Cov\left({C}_{ijs},{C}_{klt}\right)$
. Next, the required covariance is estimated as
![]() $\widehat{Cov}\left({C}_{ij+},{C}_{kl+}\right):= \sum_s{\sum}_t{N}_{ij s}{N}_{kl t}\widehat{Cov}\left({C}_{ij s},{C}_{kl t}\right)$
.
$\widehat{Cov}\left({C}_{ij+},{C}_{kl+}\right):= \sum_s{\sum}_t{N}_{ij s}{N}_{kl t}\widehat{Cov}\left({C}_{ij s},{C}_{kl t}\right)$
.
It should be noted that in the IRT application of testing the MH model, the
![]() ${N}_{ijs}$
are not fixed. By doing as if the
${N}_{ijs}$
are not fixed. By doing as if the
![]() ${N}_{ijs}$
are fixed anyway, we ignore the possibility of a correlation between
${N}_{ijs}$
are fixed anyway, we ignore the possibility of a correlation between
![]() ${C}_{ijs}$
and
${C}_{ijs}$
and
![]() ${N}_{ijs}$
. This might still entail a better approximation than assuming the identity matrix, and we will use the simulation studies to decide whether this approximation is useful.
${N}_{ijs}$
. This might still entail a better approximation than assuming the identity matrix, and we will use the simulation studies to decide whether this approximation is useful.
4.2 Estimation based on bootstrapping
4.2.1 Bootstrapping of the MCCs
In this approach, we resample
![]() $N$
rows of the data matrix with replacement and compute the MCC for each item pair
$N$
rows of the data matrix with replacement and compute the MCC for each item pair
![]() $\left(i,j\right)$
in the resample. Denote the MCC of item pair
$\left(i,j\right)$
in the resample. Denote the MCC of item pair
![]() $\left(i,j\right)$
in a resample as
$\left(i,j\right)$
in a resample as
![]() ${C}_{ij+}^{\ast }$
. We resample
${C}_{ij+}^{\ast }$
. We resample
![]() ${n}_{\mathrm{resample}}=1000$
times, thus constructing a matrix of
${n}_{\mathrm{resample}}=1000$
times, thus constructing a matrix of
![]() ${n}_{\mathrm{resample}}$
rows and
${n}_{\mathrm{resample}}$
rows and
![]() $J\left(J-1\right)/2$
columns, in which each row
$J\left(J-1\right)/2$
columns, in which each row
![]() $m$
contains the
$m$
contains the
![]() ${C}_{ij+}^{\ast }$
values of the
${C}_{ij+}^{\ast }$
values of the
![]() $m$
-th resample. Next, we compute the covariance matrix of the
$m$
-th resample. Next, we compute the covariance matrix of the
![]() ${C}_{ij+}^{\ast }$
s.
${C}_{ij+}^{\ast }$
s.
4.2.2 Bootstrapping of the Zs
In this approach, we resample
![]() $N$
rows of the data matrix with replacement and compute the Z-statistic for each item pair
$N$
rows of the data matrix with replacement and compute the Z-statistic for each item pair
![]() $\left(i,j\right)$
in the resample. Denote the Z-value of item pair
$\left(i,j\right)$
in the resample. Denote the Z-value of item pair
![]() $\left(i,j\right)$
in a resample as
$\left(i,j\right)$
in a resample as
![]() ${Z}_{ij}^{\ast }$
. We resample
${Z}_{ij}^{\ast }$
. We resample
![]() ${n}_{\mathrm{resample}}=1000$
times, thus constructing a matrix of
${n}_{\mathrm{resample}}=1000$
times, thus constructing a matrix of
![]() ${n}_{\mathrm{resample}}$
rows and
${n}_{\mathrm{resample}}$
rows and
![]() $J\left(J-1\right)/2$
columns, in which each row
$J\left(J-1\right)/2$
columns, in which each row
![]() $m$
contains the
$m$
contains the
![]() ${Z}_{ij}^{\ast }$
values of the
${Z}_{ij}^{\ast }$
values of the
![]() $m$
-th resample. Next, we compute the covariance matrix of the
$m$
-th resample. Next, we compute the covariance matrix of the
![]() ${Z}_{ij}^{\ast }$
s.
${Z}_{ij}^{\ast }$
s.
4.3 Estimation with the identity matrix
In this approach, the third method, we simply assume that the asymptotic covariance matrix of the
![]() ${Z}_{ij}$
s is the identity matrix. This is comparable to the diagonally weighted least squares (DWLS) method often used for polychoric correlations in ordinal factor analysis (Li, Reference Li2015). The reason why we suspect that the identity matrix may work well is that under MH, each conditioning group with a fixed pairwise rest score has only a small remaining variance of the latent variable, which implies that the response variables are close to independent, and independent Bernoulli variables have covariances that are asymptotically uncorrelated (Anderson & Goodman, Reference Anderson and Goodman1957).
${Z}_{ij}$
s is the identity matrix. This is comparable to the diagonally weighted least squares (DWLS) method often used for polychoric correlations in ordinal factor analysis (Li, Reference Li2015). The reason why we suspect that the identity matrix may work well is that under MH, each conditioning group with a fixed pairwise rest score has only a small remaining variance of the latent variable, which implies that the response variables are close to independent, and independent Bernoulli variables have covariances that are asymptotically uncorrelated (Anderson & Goodman, Reference Anderson and Goodman1957).
5 Aggregation of the pairwise statistics
In this section, we consider the lower-diagonal matrix of
![]() ${C}_{ij+}$
s or
${C}_{ij+}$
s or
![]() ${Z}_{ij}$
s as a vector
${Z}_{ij}$
s as a vector
![]() $\boldsymbol{y}$
in
$\boldsymbol{y}$
in
![]() ${\mathbb{R}}^{J\left(J-1\right)/2}$
. Let
${\mathbb{R}}^{J\left(J-1\right)/2}$
. Let
![]() $\boldsymbol{W}$
be the covariance matrix of
$\boldsymbol{W}$
be the covariance matrix of
![]() $\boldsymbol{y}$
as estimated in any method of the previous section. We consider various methods to aggregate
$\boldsymbol{y}$
as estimated in any method of the previous section. We consider various methods to aggregate
![]() $\boldsymbol{y}$
into an omnibus test.
$\boldsymbol{y}$
into an omnibus test.
5.1 Distance to the nonnegative cone
The theory in this section is based on order restricted statistical inference (Robertson et al., Reference Robertson, Wright and Dykstra1988). We project
![]() $\boldsymbol{y}$
onto the nonnegative cone in
$\boldsymbol{y}$
onto the nonnegative cone in
![]() ${\mathbb{R}}^{J\left(J-1\right)/2}$
, defined by
${\mathbb{R}}^{J\left(J-1\right)/2}$
, defined by
 $\mathcal{C}=\bigg\{\boldsymbol{x}\in {\mathbb{R}}^{\frac{J\left(J-1\right)}{2}}|{x}_1\ge 0,{x}_2\ge 0,\dots, {x}_{J\left(J-1\right)/2}\ge 0\bigg\}$
. We define the projection
$\mathcal{C}=\bigg\{\boldsymbol{x}\in {\mathbb{R}}^{\frac{J\left(J-1\right)}{2}}|{x}_1\ge 0,{x}_2\ge 0,\dots, {x}_{J\left(J-1\right)/2}\ge 0\bigg\}$
. We define the projection
![]() ${\boldsymbol{y}}^{\ast}$
as the point in
${\boldsymbol{y}}^{\ast}$
as the point in
![]() $\mathcal{C}$
that minimizes the squared Mahalanobis distance
$\mathcal{C}$
that minimizes the squared Mahalanobis distance
![]() ${\left(\boldsymbol{y}-{\boldsymbol{y}}^{\ast}\right)}^T{\boldsymbol{W}}^{-1}\left(\boldsymbol{y}-{\boldsymbol{y}}^{\ast}\right)$
. The chi-bar-square statistic is then defined as this squared distance, i.e.
${\left(\boldsymbol{y}-{\boldsymbol{y}}^{\ast}\right)}^T{\boldsymbol{W}}^{-1}\left(\boldsymbol{y}-{\boldsymbol{y}}^{\ast}\right)$
. The chi-bar-square statistic is then defined as this squared distance, i.e.
This result serves as the overall test statistic in the decision rules discussed in the next section. The following algorithm was used to obtain
![]() ${\boldsymbol{y}}^{\ast}$
and
${\boldsymbol{y}}^{\ast}$
and
![]() ${\overline{\chi}}^2:$
${\overline{\chi}}^2:$
-
1. Obtain the Cholesky decomposition
 ${\boldsymbol{W}}^{-1}={\boldsymbol{B}}^{\mathrm{T}}\boldsymbol{B}$
, and let
${\boldsymbol{W}}^{-1}={\boldsymbol{B}}^{\mathrm{T}}\boldsymbol{B}$
, and let
 $\boldsymbol{A} = {\boldsymbol{B}}^{-1}$
.
$\boldsymbol{A} = {\boldsymbol{B}}^{-1}$
. -
2. Compute
 $\boldsymbol{z}=\boldsymbol{By}$
. If
$\boldsymbol{z}=\boldsymbol{By}$
. If
 $\boldsymbol{W}$
is the covariance matrix of
$\boldsymbol{W}$
is the covariance matrix of
 $\boldsymbol{y}$
, then the covariance matrix of
$\boldsymbol{y}$
, then the covariance matrix of
 $\boldsymbol{z}$
is the identity matrix.
$\boldsymbol{z}$
is the identity matrix. -
3. Project
 $\boldsymbol{z}$
onto the cone
$\boldsymbol{z}$
onto the cone
 $\boldsymbol{Ax}\ge 0$
with the function coneA of the R-package coneproj (Liao & Meyer, Reference Liao and Meyer2014). Let
$\boldsymbol{Ax}\ge 0$
with the function coneA of the R-package coneproj (Liao & Meyer, Reference Liao and Meyer2014). Let
 ${\boldsymbol{z}}^{\ast}$
be the result of this projection; then
${\boldsymbol{z}}^{\ast}$
be the result of this projection; then
 ${\boldsymbol{y}}^{\ast} = \boldsymbol{A}{\boldsymbol{z}}^{\ast}$
.
${\boldsymbol{y}}^{\ast} = \boldsymbol{A}{\boldsymbol{z}}^{\ast}$
. -
4. Compute
 ${\overline{\chi}}^2 = {\left\Vert \boldsymbol{z}-{\boldsymbol{z}}^{\ast}\right\Vert}^2$
, where
${\overline{\chi}}^2 = {\left\Vert \boldsymbol{z}-{\boldsymbol{z}}^{\ast}\right\Vert}^2$
, where
 $\left\Vert \cdot \right\Vert$
is the Euclidian distance.
$\left\Vert \cdot \right\Vert$
is the Euclidian distance.
5.2 Preselected standardized partial sum of pairwise statistics
In their CARP statistics, Ellis and Sijtsma (Reference Ellis and Sijtsma2023) split the total sample of subjects into a training sample and a test sample. In our treatment hitherto, all statistics were computed with the test sample. However, one can compute
![]() ${C}_{ij+}$
in the training sample as well; denote this as
${C}_{ij+}$
in the training sample as well; denote this as
![]() ${C}_{ij+}^{\mathrm{training}}$
. Let
${C}_{ij+}^{\mathrm{training}}$
. Let
![]() ${T}_{-}$
be the set of pairs
${T}_{-}$
be the set of pairs
![]() $\left(i,j\right)$
with
$\left(i,j\right)$
with
![]() ${C}_{ij+}^{\mathrm{training}}<0$
and
${C}_{ij+}^{\mathrm{training}}<0$
and
![]() $i>j$
, and denote its size as
$i>j$
, and denote its size as
![]() $\mid {T}_{-}\mid$
. We add the corresponding values of
$\mid {T}_{-}\mid$
. We add the corresponding values of
![]() $\boldsymbol{y}$
and divide the sum by its standard error. More specifically, let
$\boldsymbol{y}$
and divide the sum by its standard error. More specifically, let
![]() ${y}_{\frac{\left(i-1\right)\left(i-2\right)}{2}+j}={C}_{ij+}$
for all
${y}_{\frac{\left(i-1\right)\left(i-2\right)}{2}+j}={C}_{ij+}$
for all
![]() $J\ge i>j\ge 1$
, and define
$J\ge i>j\ge 1$
, and define
![]() ${\boldsymbol{y}}_{-}$
as the subvector of
${\boldsymbol{y}}_{-}$
as the subvector of
![]() $\boldsymbol{y}$
containing the elements
$\boldsymbol{y}$
containing the elements
![]() ${y}_{\frac{\left(i-1\right)\left(i-2\right)}{2}+j}$
for which
${y}_{\frac{\left(i-1\right)\left(i-2\right)}{2}+j}$
for which
![]() $\left(i,j\right)\in {T}_{-}$
. Let
$\left(i,j\right)\in {T}_{-}$
. Let
![]() ${\boldsymbol{W}}_{-}$
be the submatrix of
${\boldsymbol{W}}_{-}$
be the submatrix of
![]() $\boldsymbol{W}$
, corresponding to the elements of
$\boldsymbol{W}$
, corresponding to the elements of
![]() ${\boldsymbol{y}}_{-}$
; Ellis and Sijtsma (Reference Ellis and Sijtsma2023) defined the omnibus statistic as
${\boldsymbol{y}}_{-}$
; Ellis and Sijtsma (Reference Ellis and Sijtsma2023) defined the omnibus statistic as
where
![]() $\sum$
indicates the sum over all elements in the following vector or matrix. Here, we call this omnibus test statistic the preselected standardized partial sum of pairwise statistics. For clarity, if
$\sum$
indicates the sum over all elements in the following vector or matrix. Here, we call this omnibus test statistic the preselected standardized partial sum of pairwise statistics. For clarity, if
![]() $\boldsymbol{y}$
contains the
$\boldsymbol{y}$
contains the
![]() ${Z}_{ij}$
s and
${Z}_{ij}$
s and
![]() $\boldsymbol{W}$
is assumed to be the identity matrix, then
$\boldsymbol{W}$
is assumed to be the identity matrix, then
 $$\begin{align*}{Z}_{\mathrm{PS}}=\frac{\sum \left\{{Z}_{ij}|\left(i,j\right)\in {T}_{-}\right\}}{\sqrt{\mid {T}_{-}\mid }}.\end{align*}$$
$$\begin{align*}{Z}_{\mathrm{PS}}=\frac{\sum \left\{{Z}_{ij}|\left(i,j\right)\in {T}_{-}\right\}}{\sqrt{\mid {T}_{-}\mid }}.\end{align*}$$
5.3 Conditionalized multiple testing procedures
Ellis et al. (Reference Ellis, Pecanka and Goeman2018) argued that multiple testing procedures for interval hypotheses can be enhanced with the following general adaptation: Pick some real number
![]() $\lambda \in \left(0,1\right]$
, and select only the p-values with
$\lambda \in \left(0,1\right]$
, and select only the p-values with
![]() ${p}_i<\lambda$
, and divide each
${p}_i<\lambda$
, and divide each
![]() ${p}_i$
by
${p}_i$
by
![]() $\lambda$
; then, apply an ordinary multiple testing procedure, such as the Bonferroni correction or the Benjamini-Hochberg correction, to the resulting set. That is, apply an ordinary multiple testing procedure to the set of corrected
$\lambda$
; then, apply an ordinary multiple testing procedure, such as the Bonferroni correction or the Benjamini-Hochberg correction, to the resulting set. That is, apply an ordinary multiple testing procedure to the set of corrected
![]() $p$
-values
$p$
-values
![]() $\left\{{p}_i/\lambda :{p}_i<\lambda \right\}$
. Ellis et al. argue that this procedure often controls the Type 1 error, certainly with independent
$\left\{{p}_i/\lambda :{p}_i<\lambda \right\}$
. Ellis et al. argue that this procedure often controls the Type 1 error, certainly with independent
![]() $p$
-values, and also with non-independent
$p$
-values, and also with non-independent
![]() $p$
-values if the number of
$p$
-values if the number of
![]() $p$
-values is large and the Bonferroni-correction is used. They show that this procedure increases the power if the
$p$
-values is large and the Bonferroni-correction is used. They show that this procedure increases the power if the
![]() $p$
-values are supra-uniform; that is, if most
$p$
-values are supra-uniform; that is, if most
![]() $p$
-values are higher than would be expected in a uniform distribution. We expect that the latter condition is often fulfilled in the situation under investigation here, where the
$p$
-values are higher than would be expected in a uniform distribution. We expect that the latter condition is often fulfilled in the situation under investigation here, where the
![]() $p$
-values test whether conditional covariances are nonnegative in the context of MH. If MH holds and the item response functions are not flat, then the conditional covariances will be positive, yielding supra-uniform
$p$
-values test whether conditional covariances are nonnegative in the context of MH. If MH holds and the item response functions are not flat, then the conditional covariances will be positive, yielding supra-uniform
![]() $p$
-values.
$p$
-values.
Ellis et al. (Reference Ellis, Pecanka and Goeman2018) investigated their conditionalization procedure with the multiple testing methods Davidov (Reference Davidov2011) discussed in the context of independent
![]() $p$
-values, and we will apply some of these multiple testing methods here. Davidov recommended using the
$p$
-values, and we will apply some of these multiple testing methods here. Davidov recommended using the
![]() ${I}_{+}$
statistics, but the method that he labelled “normal” achieved similar power (Davidov, p. 2439–2440). The latter method means that the
${I}_{+}$
statistics, but the method that he labelled “normal” achieved similar power (Davidov, p. 2439–2440). The latter method means that the
![]() $p$
-values are converted to standard normal
$p$
-values are converted to standard normal
![]() $Z$
-statistics and added, and this method is the natural candidate if the test statistics underlying the
$Z$
-statistics and added, and this method is the natural candidate if the test statistics underlying the
![]() $p$
-values are normal. Applied to the present situation with the conditionalization rule of Ellis et al. (Reference Ellis, Pecanka and Goeman2018) and
$p$
-values are normal. Applied to the present situation with the conditionalization rule of Ellis et al. (Reference Ellis, Pecanka and Goeman2018) and
![]() $\lambda =0.5$
, this amounts to the following. Let
$\lambda =0.5$
, this amounts to the following. Let
![]() $S$
be the set of pairs
$S$
be the set of pairs
![]() $i>j$
with
$i>j$
with
![]() ${Z}_{ij}<0$
in the test sample, and denote its size as
${Z}_{ij}<0$
in the test sample, and denote its size as
![]() $\mid S\mid$
. A test statistic based on the conditionalized sum is
$\mid S\mid$
. A test statistic based on the conditionalized sum is
 $$\begin{align*}{Z}_{\mathrm{CS}}:= \frac{\sum \left\{{\Phi}^{-1}\left(2\Phi \left({Z}_{ij}\right)\right)|\left(i,j\right)\in S\right\}}{\sqrt{\left|S\right|}},\end{align*}$$
$$\begin{align*}{Z}_{\mathrm{CS}}:= \frac{\sum \left\{{\Phi}^{-1}\left(2\Phi \left({Z}_{ij}\right)\right)|\left(i,j\right)\in S\right\}}{\sqrt{\left|S\right|}},\end{align*}$$
where
![]() $S$
is the number of pairs
$S$
is the number of pairs
![]() $i<j$
with
$i<j$
with
![]() ${Z}_{ij}<0$
. However, the statistic that was most powerful in the simulations, Ellis et al. reported was the product of
${Z}_{ij}<0$
. However, the statistic that was most powerful in the simulations, Ellis et al. reported was the product of
![]() $p$
-values, which Davidov attributed to Fisher. In the present situation, after a log-transformation of the conditionalized product, we obtain,
$p$
-values, which Davidov attributed to Fisher. In the present situation, after a log-transformation of the conditionalized product, we obtain,
which is compared to a chi-square distribution with
![]() $df=2\mid S\mid$
.
$df=2\mid S\mid$
.
Finally, we consider the Bonferroni correction because it is so easy and well-known despite the general consensus that more powerful alternatives exist. In conditionalized form, this amounts to
Note that all three statistics,
![]() ${Z}_{\mathrm{CS}}$
,
${Z}_{\mathrm{CS}}$
,
![]() ${Q}_{\mathrm{CP}}$
, and
${Q}_{\mathrm{CP}}$
, and
![]() ${p}_{\mathrm{CB}}$
, ignore the correlations of the
${p}_{\mathrm{CB}}$
, ignore the correlations of the
![]() ${Z}_{ij}$
s. In
${Z}_{ij}$
s. In
![]() ${Z}_{\mathrm{CS}}$
and
${Z}_{\mathrm{CS}}$
and
![]() ${Q}_{\mathrm{CP}}$
, it is implicitly assumed that the
${Q}_{\mathrm{CP}}$
, it is implicitly assumed that the
![]() ${Z}_{ij}$
s are uncorrelated, and we are not certain that they control the Type 1 error in correlated cases. However, the correlations between pairwise CARP statistics might be so small that it hardly affect the distribution, as we argued in the section where we proposed the identity matrix. Therefore, we study these statistics despite the uncertainty about possibly correlated
${Z}_{ij}$
s are uncorrelated, and we are not certain that they control the Type 1 error in correlated cases. However, the correlations between pairwise CARP statistics might be so small that it hardly affect the distribution, as we argued in the section where we proposed the identity matrix. Therefore, we study these statistics despite the uncertainty about possibly correlated
![]() ${Z}_{ij}$
s.
${Z}_{ij}$
s.
5.4 Preselection with multiple testing procedures
The idea of a preselection of item pairs based on the training sample can also be applied to multiple testing procedures, like the conditionalization principle Ellis et al. (Reference Ellis, Pecanka and Goeman2018) discussed. Suppose the data sample is randomly split into a training sample and a test sample. Let the training data matrix be denoted as
![]() ${\boldsymbol{D}}_1$
and the test data matrix as
${\boldsymbol{D}}_1$
and the test data matrix as
![]() ${\boldsymbol{D}}_2$
, where
${\boldsymbol{D}}_2$
, where
![]() ${\boldsymbol{D}}_1$
and
${\boldsymbol{D}}_1$
and
![]() ${\boldsymbol{D}}_2$
are independent. Suppose that for each subset
${\boldsymbol{D}}_2$
are independent. Suppose that for each subset
![]() $L$
of pairs of variables in
$L$
of pairs of variables in
![]() ${\boldsymbol{D}}_2$
there is a multiple testing procedure
${\boldsymbol{D}}_2$
there is a multiple testing procedure
![]() ${M}_L$
that controls the Type I error when it is applied to
${M}_L$
that controls the Type I error when it is applied to
![]() $L$
. More precisely,
$L$
. More precisely,
![]() ${M}_L$
is a function that is applied to
${M}_L$
is a function that is applied to
![]() ${\boldsymbol{D}}_2$
and only uses the pairs of variables in
${\boldsymbol{D}}_2$
and only uses the pairs of variables in
![]() $L$
, resulting in a 1 (reject) or 0 (no reject) decision, with
$L$
, resulting in a 1 (reject) or 0 (no reject) decision, with
![]() $P\left({M}_L\left({\boldsymbol{D}}_2\right)=1\right)\le \alpha$
if the null hypothesis is true, where
$P\left({M}_L\left({\boldsymbol{D}}_2\right)=1\right)\le \alpha$
if the null hypothesis is true, where
![]() $\alpha$
is the nominal level of significance. Suppose that we chose
$\alpha$
is the nominal level of significance. Suppose that we chose
![]() $L$
as a function of
$L$
as a function of
![]() ${\boldsymbol{D}}_1$
; let this function be denoted as
${\boldsymbol{D}}_1$
; let this function be denoted as
![]() $\Lambda$
with range
$\Lambda$
with range
![]() $R\left(\Lambda \right)$
. An example of this would be that
$R\left(\Lambda \right)$
. An example of this would be that
![]() $\Lambda$
selects the pairs with negative conditional covariances and
$\Lambda$
selects the pairs with negative conditional covariances and
![]() ${M}_L$
uses the p-values
${M}_L$
uses the p-values
![]() ${p}_{ij}=\Phi \left({Z}_{ij}\right)$
of
${p}_{ij}=\Phi \left({Z}_{ij}\right)$
of
![]() $\left(i,j\right)\in L$
with the Bonferroni correction. That is,
$\left(i,j\right)\in L$
with the Bonferroni correction. That is,
![]() $\Lambda \left({\boldsymbol{D}}_1\right) = \left\{\left(i,j\right):{C}_{ij+}^{\mathrm{training}}<0\;\mathrm{and}\;i>j\right\}$
and
$\Lambda \left({\boldsymbol{D}}_1\right) = \left\{\left(i,j\right):{C}_{ij+}^{\mathrm{training}}<0\;\mathrm{and}\;i>j\right\}$
and
![]() ${M}_L=1\Longleftrightarrow \min \left\{{p}_{ij}\left|L\right|\right\}\le \alpha$
. Then
${M}_L=1\Longleftrightarrow \min \left\{{p}_{ij}\left|L\right|\right\}\le \alpha$
. Then
![]() ${M}_{\Lambda \left({\boldsymbol{D}}_1\right)}\left({\boldsymbol{D}}_2\right)$
is the procedure that applies the Bonferroni correction to p-values in the test sample using only pairs that have a negative conditional covariance in the training sample. Such procedures control the Type I error rate: Since
${M}_{\Lambda \left({\boldsymbol{D}}_1\right)}\left({\boldsymbol{D}}_2\right)$
is the procedure that applies the Bonferroni correction to p-values in the test sample using only pairs that have a negative conditional covariance in the training sample. Such procedures control the Type I error rate: Since
![]() ${\boldsymbol{D}}_1$
and
${\boldsymbol{D}}_1$
and
![]() ${\boldsymbol{D}}_2$
are independent, the conditional distribution of
${\boldsymbol{D}}_2$
are independent, the conditional distribution of
![]() ${\boldsymbol{D}}_2$
given
${\boldsymbol{D}}_2$
given
![]() $\Lambda \left({\boldsymbol{D}}_1\right)$
is the same as the unconditional distribution of
$\Lambda \left({\boldsymbol{D}}_1\right)$
is the same as the unconditional distribution of
![]() ${\boldsymbol{D}}_2$
, so the rejection rate is
${\boldsymbol{D}}_2$
, so the rejection rate is
Thus, we may calculate p-values for conditional covariances in the test data using only the pairs that have a negative conditional covariance in the training sample and then apply a multiple testing procedure to this selection as if it were the entire test data set from the outset. Applying this procedure to the statistics of the previous section, we obtain the following results. Let
![]() ${T}_{-}$
be the set of pairs
${T}_{-}$
be the set of pairs
![]() $\left(i,j\right)$
with
$\left(i,j\right)$
with
![]() ${C}_{ij+}^{\mathrm{training}}<0$
and
${C}_{ij+}^{\mathrm{training}}<0$
and
![]() $i>j$
. Then
$i>j$
. Then
with
![]() $df=2\mid {T}_{-}\mid, \mid$
where
$df=2\mid {T}_{-}\mid, \mid$
where
![]() $\mid {T}_{-}\mid$
is the size of
$\mid {T}_{-}\mid$
is the size of
![]() ${T}_{-}$
. Similarly,
${T}_{-}$
. Similarly,
6 Decision rules
6.1 Decision rules: the LR test and the conditional LR test
In this section, we consider two decision rules based on
![]() ${\overline{\chi}}^2$
. The first decision rule uses the unconditional distribution of
${\overline{\chi}}^2$
. The first decision rule uses the unconditional distribution of
![]() ${\overline{\chi}}^2$
. The second decision rule uses the conditional distribution of
${\overline{\chi}}^2$
. The second decision rule uses the conditional distribution of
![]() ${\overline{\chi}}^2$
, given the dimensionality of the boundary hyperplane that contains
${\overline{\chi}}^2$
, given the dimensionality of the boundary hyperplane that contains
![]() ${\boldsymbol{y}}^{\ast}$
. If
${\boldsymbol{y}}^{\ast}$
. If
![]() $\boldsymbol{W}$
is the identity matrix, then this dimensionality is equal to the number of negative MCCs. Both the
$\boldsymbol{W}$
is the identity matrix, then this dimensionality is equal to the number of negative MCCs. Both the
![]() ${C}_{ij+}$
s and the
${C}_{ij+}$
s and the
![]() ${Z}_{ij}$
s have an asymptotic multivariate normal distribution as
${Z}_{ij}$
s have an asymptotic multivariate normal distribution as
![]() $N\to \infty$
(Browne, Reference Browne1984, proposition 2). Therefore, we assume a multivariate normal distribution for
$N\to \infty$
(Browne, Reference Browne1984, proposition 2). Therefore, we assume a multivariate normal distribution for
![]() $\boldsymbol{y}$
, which is either the vector of
$\boldsymbol{y}$
, which is either the vector of
![]() ${C}_{ij+}$
s or the vector of
${C}_{ij+}$
s or the vector of
![]() ${Z}_{ij}$
s.
${Z}_{ij}$
s.
First, we consider the likelihood ratio (LR) test. Using this test, we reject the null hypothesis if
![]() ${\overline{\chi}}^2$
exceeds a critical level (Robertson et al., Reference Robertson, Wright and Dykstra1988). Under the least favorable case of the null hypothesis, where
${\overline{\chi}}^2$
exceeds a critical level (Robertson et al., Reference Robertson, Wright and Dykstra1988). Under the least favorable case of the null hypothesis, where
![]() $Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)=0\;\mathrm{for}\;\mathrm{all}\;i,j=1,\dots, J;s=1,\dots, \max {R}_{ij}$
, the distribution of
$Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)=0\;\mathrm{for}\;\mathrm{all}\;i,j=1,\dots, J;s=1,\dots, \max {R}_{ij}$
, the distribution of
![]() ${\overline{\chi}}^2$
is a weighted average of chi-square distributions (Robertson et al., Reference Robertson, Wright and Dykstra1988):
${\overline{\chi}}^2$
is a weighted average of chi-square distributions (Robertson et al., Reference Robertson, Wright and Dykstra1988):
 $$\begin{align*}P\left({\overline{\chi}}^2>c\right)=\sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}P\left({\chi}_r^2>c\right)P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right).\end{align*}$$
$$\begin{align*}P\left({\overline{\chi}}^2>c\right)=\sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}P\left({\chi}_r^2>c\right)P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right).\end{align*}$$
We estimated the weights
![]() $P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right)$
by drawing from a multivariate normal distribution with a covariance matrix
$P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right)$
by drawing from a multivariate normal distribution with a covariance matrix
![]() $\boldsymbol{W}$
, and counting for each draw how many coordinates are negative. We used
$\boldsymbol{W}$
, and counting for each draw how many coordinates are negative. We used
![]() ${10}^5$
draws. Denote the estimated probability of getting
${10}^5$
draws. Denote the estimated probability of getting
![]() $r$
negative coordinates as
$r$
negative coordinates as
![]() ${\overset{\sim }{p}}_r$
. The
${\overset{\sim }{p}}_r$
. The
![]() $p$
-value for the observed chi-bar-squared is obtained as
$p$
-value for the observed chi-bar-squared is obtained as
 $$\begin{align*}{p}_{\mathrm{LR}}:= \sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}P\left({\chi}_r^2>{\overline{\chi}}_{obs}^2\right){\overset{\sim }{p}}_r.\end{align*}$$
$$\begin{align*}{p}_{\mathrm{LR}}:= \sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}P\left({\chi}_r^2>{\overline{\chi}}_{obs}^2\right){\overset{\sim }{p}}_r.\end{align*}$$
The null hypothesis is rejected if
![]() ${p}_{\mathrm{LR}}<\alpha$
.
${p}_{\mathrm{LR}}<\alpha$
.
Second, we consider the conditional test based on Wollan and Dykstra (Reference Wollan and Dykstra1986). Ellis et al. (Reference Ellis, Pecanka and Goeman2018) generalized the conditionalization principle to other multiple testing procedures with one-sided hypotheses and demonstrated that conditionalization achieves a strong gain in power if most null hypotheses are true, a situation that can be expected here. We also discuss other conditional tests; therefore, we call this test the conditional likelihood (CL) ratio test.
Let
![]() $dh\left({\boldsymbol{y}}^{\ast}\right)$
be the dimensionality of the boundary hyperplane on which
$dh\left({\boldsymbol{y}}^{\ast}\right)$
be the dimensionality of the boundary hyperplane on which
![]() $\boldsymbol{y}$
is projected, and let
$\boldsymbol{y}$
is projected, and let
![]() $df\left({\boldsymbol{y}}^{\ast}\right) = \frac{J\left(J-1\right)}{2}- dh\left({\boldsymbol{y}}^{\ast}\right)$
. Wollan and Dykstra explain that the conditional distribution of
$df\left({\boldsymbol{y}}^{\ast}\right) = \frac{J\left(J-1\right)}{2}- dh\left({\boldsymbol{y}}^{\ast}\right)$
. Wollan and Dykstra explain that the conditional distribution of
![]() ${\overline{\chi}}^2$
given
${\overline{\chi}}^2$
given
![]() $df\left({\boldsymbol{y}}^{\ast}\right) = r$
is a chi-square distribution with
$df\left({\boldsymbol{y}}^{\ast}\right) = r$
is a chi-square distribution with
![]() $r$
degrees of freedom if
$r$
degrees of freedom if
![]() $r>0$
. Let
$r>0$
. Let
![]() ${\chi}_r^2\left(\alpha \right)$
be the right-sided critical value for nominal significance level
${\chi}_r^2\left(\alpha \right)$
be the right-sided critical value for nominal significance level
![]() $\alpha$
in a chi-square distribution with
$\alpha$
in a chi-square distribution with
![]() $r$
degrees of freedom; that is,
$r$
degrees of freedom; that is,
![]() $P\left({\chi}_r^2>{\chi}_r^2\left(\alpha \right)\right)=\alpha$
. In the conditional test, we reject the null hypothesis if both
$P\left({\chi}_r^2>{\chi}_r^2\left(\alpha \right)\right)=\alpha$
. In the conditional test, we reject the null hypothesis if both
![]() $df\left({\boldsymbol{y}}^{\ast}\right)>0$
and
$df\left({\boldsymbol{y}}^{\ast}\right)>0$
and
![]() ${\overline{\chi}}^2>{\chi}_{df\left({\boldsymbol{y}}^{\ast}\right)}^2\left(\alpha \right)$
. Assuming a multivariate normal distribution, the Type 1 error rate of the conditional test is less than
${\overline{\chi}}^2>{\chi}_{df\left({\boldsymbol{y}}^{\ast}\right)}^2\left(\alpha \right)$
. Assuming a multivariate normal distribution, the Type 1 error rate of the conditional test is less than
![]() $\alpha$
, because, as pointed out by Wollan and Dykstra,
$\alpha$
, because, as pointed out by Wollan and Dykstra,
 $$\begin{align*}P\left(\mathrm{reject}\;{\mathrm{H}}_0\right)&=\sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}P\left({\overline{\chi}}^2>{\chi}_r^2\left(\alpha \right)| df\left({\boldsymbol{y}}^{\ast}\right) = r\right)P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right)\\&=\sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}\alpha P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right)=\alpha \left(1-P\left( df\left({\boldsymbol{y}}^{\ast}\right) = 0\right)\right).\end{align*}$$
$$\begin{align*}P\left(\mathrm{reject}\;{\mathrm{H}}_0\right)&=\sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}P\left({\overline{\chi}}^2>{\chi}_r^2\left(\alpha \right)| df\left({\boldsymbol{y}}^{\ast}\right) = r\right)P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right)\\&=\sum \limits_{r=1}^{\frac{J\left(J-2\right)}{2}}\alpha P\left( df\left({\boldsymbol{y}}^{\ast}\right) = r\right)=\alpha \left(1-P\left( df\left({\boldsymbol{y}}^{\ast}\right) = 0\right)\right).\end{align*}$$
The event
![]() $df\left({\boldsymbol{y}}^{\ast}\right) = 0$
corresponds to
$df\left({\boldsymbol{y}}^{\ast}\right) = 0$
corresponds to
![]() ${\boldsymbol{y}}^{\ast} = \boldsymbol{y}$
, which would happen if all
${\boldsymbol{y}}^{\ast} = \boldsymbol{y}$
, which would happen if all
![]() ${C}_{ij+}$
or
${C}_{ij+}$
or
![]() ${Z}_{ij}$
are nonnegative. Wollan and Dykstra continue to estimate this factor, but this probability is small for five items or more, and therefore it is ignored here, consistent with Ellis et al. (Reference Ellis, Pecanka and Goeman2018). In sum, we define
${Z}_{ij}$
are nonnegative. Wollan and Dykstra continue to estimate this factor, but this probability is small for five items or more, and therefore it is ignored here, consistent with Ellis et al. (Reference Ellis, Pecanka and Goeman2018). In sum, we define
6.2 Decision rules: other tests
The p-values of the other tests are computed using
where
![]() $\Phi$
is the standard normal cumulative distribution function and
$\Phi$
is the standard normal cumulative distribution function and
![]() ${G}_k^2$
is the chi-square survival function with
${G}_k^2$
is the chi-square survival function with
![]() $k$
degrees of freedom. The corrected p-values
$k$
degrees of freedom. The corrected p-values
![]() ${p}_{\mathrm{CB}}$
and
${p}_{\mathrm{CB}}$
and
![]() ${p}_{\mathrm{PB}}$
are used without further correction.
${p}_{\mathrm{PB}}$
are used without further correction.
7 Comparison with competing methods
We compare our statistics with the two prominent alternative methods for the proposed test, which are the DIMTEST or DETECT procedures for analysis of essential dimensionality. DIMTEST and DETECT are two procedures based on Stout’s (Reference Stout1987) theory of essential dimensionality (also Stout et al. Reference Stout, Habing, Douglas, Kim, Roussos and Zhang1996). DIMTEST has a confirmative approach that tests unidimensionality, whereas DETECT was created as an explorative approach that divides the set of test items into clusters that are associated with different dimensions. Li et al. (Reference Li, Habing and Roussos2017, p. 210) summarize DIMTEST as follows:
The DIMTEST procedure (Nandakumar, Yu, Li, & Stout, 1998; Stout, Reference Stout1987; Stout, Froelich, & Gao, 2001) is often used to test the null hypothesis that an exam is locally independent and unidimensional. It does this by dividing the test into two subtests (an assessment subtest called AT and a partitioning subtest called PT) and testing whether there are any local dependencies among the AT items, conditioned on the score on the partitioning test. DIMTEST has been widely studied for dichotomous item exams and has good power when AT and PT are chosen well (e.g., Froelich & Habing, Reference Froelich and Habing2008). If AT and PT are chosen poorly (e.g., both are random samples of items), the procedure will have power near 0.
Like a non-aggregated CARP test, DIMTEST uses conditional covariances, but whereas a CARP test rejects unidimensionality if the conditional covariances are negative, DIMTEST rejects unidimensionality if the conditional covariances are too high. Both CARP tests and DIMTEST divide the set of items into a partitioning test and an assessment test first, but CARP tests restrict the assessment test to a pair of items. Our new aggregated CARP (ACARP) test avoids this problem of selecting an assessment test by aggregating the individual CARP tests across item pairs. DIMTEST handles this problem by splitting the test based on factor analysis in a training sample, and the procedure can be improved further with bootstrapping (Froelich & Habing, Reference Froelich and Habing2008). DIMTEST is based on the statistic
 $$\begin{align*}T=\sum \limits_{\begin{array}{c}i,j\in AT\\ {}i\ne j\end{array}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|\Theta \right)\right).\end{align*}$$
$$\begin{align*}T=\sum \limits_{\begin{array}{c}i,j\in AT\\ {}i\ne j\end{array}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|\Theta \right)\right).\end{align*}$$
A sample estimate
![]() $\widehat{T}$
of
$\widehat{T}$
of
![]() $T$
is obtained by replacing
$T$
is obtained by replacing
![]() $\Theta$
with an estimate
$\Theta$
with an estimate
![]() $\widehat{\Theta}$
based on the partitioning test, usually the sum score. Stout (Reference Stout1987) argued that
$\widehat{\Theta}$
based on the partitioning test, usually the sum score. Stout (Reference Stout1987) argued that
![]() $Cov\left({X}_i,{X}_j|\Theta \right)=0$
if the test is unidimensional, and, therefore,
$Cov\left({X}_i,{X}_j|\Theta \right)=0$
if the test is unidimensional, and, therefore,
![]() $Cov\left({X}_i,{X}_j|\widehat{\Theta}\right)\approx 0$
if
$Cov\left({X}_i,{X}_j|\widehat{\Theta}\right)\approx 0$
if
![]() $\widehat{\Theta}$
is a good estimate of
$\widehat{\Theta}$
is a good estimate of
![]() $\Theta$
. A high value of
$\Theta$
. A high value of
![]() $\widehat{T}$
means that the test is not unidimensional. This may be due to multi-dimensionality or lack of local independence. Several adjustments and improvements of DIMTEST have been suggested to estimate or reduce the bias in
$\widehat{T}$
means that the test is not unidimensional. This may be due to multi-dimensionality or lack of local independence. Several adjustments and improvements of DIMTEST have been suggested to estimate or reduce the bias in
![]() $\widehat{T}$
caused by
$\widehat{T}$
caused by
![]() $\widehat{\Theta}$
being a fallible estimate of
$\widehat{\Theta}$
being a fallible estimate of
![]() $\Theta$
(e.g., Kieftenbeld & Nandakumar, Reference Kieftenbeld and Nandakumar2015), especially if the number of items is small.
$\Theta$
(e.g., Kieftenbeld & Nandakumar, Reference Kieftenbeld and Nandakumar2015), especially if the number of items is small.
DETECT is a method to cluster items based on their conditional covariances. The clustering is based on Zhang and Stout’s (1999) theory of conditional covariances for tests with a simple structure. The procedure produces a clustering of the items, and a unidimensional test should result in one cluster that contains all items. This is an explorative method, and not a statistical significance test. For a given partition
![]() $\mathcal{P}$
of the set of test items (that is,
$\mathcal{P}$
of the set of test items (that is,
![]() $\left\{1,\dots, J\right\}$
in our notation), the theoretical DETECT index is
$\left\{1,\dots, J\right\}$
in our notation), the theoretical DETECT index is
 $$\begin{align*}D:= \frac{1}{J\left(J-1\right)}\sum \limits_{\begin{array}{c}i,j\in TT\\ {}i\ne j\end{array}}{\delta}_{ij}^{\mathcal{P}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|\Theta \right)\right),\end{align*}$$
$$\begin{align*}D:= \frac{1}{J\left(J-1\right)}\sum \limits_{\begin{array}{c}i,j\in TT\\ {}i\ne j\end{array}}{\delta}_{ij}^{\mathcal{P}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|\Theta \right)\right),\end{align*}$$
where
![]() $TT$
is the set of all items in the test, and
$TT$
is the set of all items in the test, and
![]() ${\delta}_{ij}^{\mathcal{P}}=1$
if
${\delta}_{ij}^{\mathcal{P}}=1$
if
![]() $i$
and
$i$
and
![]() $j$
are elements of the same cluster in
$j$
are elements of the same cluster in
![]() $\mathcal{P}$
, and
$\mathcal{P}$
, and
![]() ${\delta}_{ij}^{\mathcal{P}}=-1$
otherwise. DETECT searches for the partition that maximizes
${\delta}_{ij}^{\mathcal{P}}=-1$
otherwise. DETECT searches for the partition that maximizes
![]() $D$
using an estimate
$D$
using an estimate
![]() $\widehat{\Theta}$
that replaces
$\widehat{\Theta}$
that replaces
![]() $\Theta$
, leading to a sample estimate
$\Theta$
, leading to a sample estimate
![]() $\widehat{D}$
of
$\widehat{D}$
of
![]() $D$
. Many adjustments and improvements of DETECT have been suggested to estimate or reduce the bias in
$D$
. Many adjustments and improvements of DETECT have been suggested to estimate or reduce the bias in
![]() $\widehat{D}$
caused by
$\widehat{D}$
caused by
![]() $\widehat{\Theta}$
being a fallible estimate of
$\widehat{\Theta}$
being a fallible estimate of
![]() $\Theta$
(Roussos & Ozbek, Reference Roussos and Ozbek2006; Zhang, Reference Zhang2007), especially if the number of items is small.
$\Theta$
(Roussos & Ozbek, Reference Roussos and Ozbek2006; Zhang, Reference Zhang2007), especially if the number of items is small.
Considering the relationship between DIMTEST and DETECT, we study how DETECT could be used as a confirmatory test of unidimensionality. It would then be logical to define
![]() $\mathcal{P}$
as one cluster that contains all items, and the theoretical DETECT index for this would be
$\mathcal{P}$
as one cluster that contains all items, and the theoretical DETECT index for this would be
 $$\begin{align*}{D}_1:= \frac{1}{J\left(J-1\right)}\sum \limits_{\begin{array}{c}i,j\in TT\\ {}i\ne j\end{array}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|\Theta \right)\right).\end{align*}$$
$$\begin{align*}{D}_1:= \frac{1}{J\left(J-1\right)}\sum \limits_{\begin{array}{c}i,j\in TT\\ {}i\ne j\end{array}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|\Theta \right)\right).\end{align*}$$
Aside from the factor
![]() $1/J\left(J-1\right)$
, one could describe
$1/J\left(J-1\right)$
, one could describe
![]() ${D}_1$
as an instance of
${D}_1$
as an instance of
![]() $T$
where both the assessment test and the partitioning test contain all items. A high value of
$T$
where both the assessment test and the partitioning test contain all items. A high value of
![]() ${D}_1$
would lead to the conclusion that the test is not unidimensional.
${D}_1$
would lead to the conclusion that the test is not unidimensional.
For the sake of comparison, a single CARP test would test whether
![]() $\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)\ge 0$
, where
$\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)\ge 0$
, where
![]() ${\widehat{\Theta}}_i$
and
${\widehat{\Theta}}_i$
and
![]() ${\widehat{\Theta}}_j$
are predictors of
${\widehat{\Theta}}_j$
are predictors of
![]() ${X}_i$
and
${X}_i$
and
![]() ${X}_j$
, respectively, based on the items excluding
${X}_j$
, respectively, based on the items excluding
![]() $i$
and
$i$
and
![]() $j$
. The
$j$
. The
![]() ${Z}_{\mathrm{PS}}$
statistic based on the pairwise MCCs
${Z}_{\mathrm{PS}}$
statistic based on the pairwise MCCs
![]() ${C}_{ij+}$
, as defined earlier, can be considered a sample estimate of the theoretical index
${C}_{ij+}$
, as defined earlier, can be considered a sample estimate of the theoretical index
 $$\begin{align*}{\zeta}_{PS}:= \frac{\sum \limits_{\left(i,j\right)\in {T}_{-}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)}{\sqrt{\sum {\boldsymbol{\Omega}}_{-}}},\end{align*}$$
$$\begin{align*}{\zeta}_{PS}:= \frac{\sum \limits_{\left(i,j\right)\in {T}_{-}}\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)}{\sqrt{\sum {\boldsymbol{\Omega}}_{-}}},\end{align*}$$
where
![]() ${T}_{-}$
consists of the pairs for which
${T}_{-}$
consists of the pairs for which
![]() $\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)<0$
and
$\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)<0$
and
![]() $i<j$
in the training sample, and
$i<j$
in the training sample, and
![]() ${\boldsymbol{\Omega}}_{-}$
is the covariance matrix used for normalization. A negative value of
${\boldsymbol{\Omega}}_{-}$
is the covariance matrix used for normalization. A negative value of
![]() ${\zeta}_{PS}$
would lead to the conclusion that the test is not unidimensional. The DIMTEST index
${\zeta}_{PS}$
would lead to the conclusion that the test is not unidimensional. The DIMTEST index
![]() $\widehat{T}$
and the DETECT index
$\widehat{T}$
and the DETECT index
![]() ${\widehat{D}}_1$
thus have a structure that is very similar to the
${\widehat{D}}_1$
thus have a structure that is very similar to the
![]() ${Z}_{\mathrm{PS}}$
statistic before the latter is normalized with
${Z}_{\mathrm{PS}}$
statistic before the latter is normalized with
![]() $\sqrt{\sum {\boldsymbol{\Omega}}_{-}}$
. The main difference is that they are computed using different pairs
$\sqrt{\sum {\boldsymbol{\Omega}}_{-}}$
. The main difference is that they are computed using different pairs
![]() $\left(i,j\right)$
. While DIMTEST would use pairs with high conditional covariances in the training sample,
$\left(i,j\right)$
. While DIMTEST would use pairs with high conditional covariances in the training sample,
![]() ${Z}_{\mathrm{PS}}$
would use pairs with low conditional covariances in the training sample. Note that if
${Z}_{\mathrm{PS}}$
would use pairs with low conditional covariances in the training sample. Note that if
![]() ${\widehat{\Theta}}_i$
and
${\widehat{\Theta}}_i$
and
![]() ${\widehat{\Theta}}_j$
are poor estimates,
${\widehat{\Theta}}_j$
are poor estimates,
![]() $\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)$
must still be nonnegative, and therefore ACARP does not require bias corrections in order to control the Type I error rate.
$\mathbb{E}\left( Cov\left({X}_i,{X}_j|{\widehat{\Theta}}_i+{\widehat{\Theta}}_j\right)\right)$
must still be nonnegative, and therefore ACARP does not require bias corrections in order to control the Type I error rate.
DIMTEST, DETECT, and the ACARP tests developed here are closely related. The main difference is the choice of the targeted item pairs and the conditioning variable and the implications that this has for the sign of the covariances. In DIMTEST and DETECT, the conditioning variable is supposed to capture the partitioning test, and unidimensionality is rejected if the conditional covariances in the assessment test are high. In the ACARP tests, one would rather combine covariances of pairs from different dimensions; the conditioning variables are supposed to predict the assessment items, and unidimensionality is rejected if the conditional covariances are negative. For example, if the test has two dimensions
![]() $A$
and
$A$
and
![]() $B$
, DIMTEST would use
$B$
, DIMTEST would use
![]() $A$
as the assessment test and
$A$
as the assessment test and
![]() $B$
as the partitioning test, or conversely; but
$B$
as the partitioning test, or conversely; but
![]() ${Z}_{\mathrm{PS}}$
would use pairs
${Z}_{\mathrm{PS}}$
would use pairs
![]() $\left(i,j\right)$
with
$\left(i,j\right)$
with
![]() $i\in A$
and
$i\in A$
and
![]() $j\in B$
.
$j\in B$
.
8 Simulation study I: preliminary selection of test methods
We investigated whether the Type 1 error rate is under control in typical IRT cases, and we compared our test methods on statistical power. In the first simulation study, we aimed to make a preliminary selection of the most promising test methods, which we investigated further in the second and third simulation studies. We used
![]() $J$
items and a logistic model,
$J$
items and a logistic model,
where
![]() $\left({\Theta}_1,{\Theta}_2\right)$
has a bivariate standard normal distribution with correlation 0. Denote the number of items that load on dimensions 1 and 2 as
$\left({\Theta}_1,{\Theta}_2\right)$
has a bivariate standard normal distribution with correlation 0. Denote the number of items that load on dimensions 1 and 2 as
![]() ${J}_1$
and
${J}_1$
and
![]() ${J}_2$
, respectively, so that
${J}_2$
, respectively, so that
![]() ${J}_1+{J}_2=J$
.
${J}_1+{J}_2=J$
.
For the first simulations, we used
![]() $J=10$
. We studied three possible dimensionality cases:
$J=10$
. We studied three possible dimensionality cases:
-
• Dimensionality 0: In this case,
 ${\alpha}_{i1}={\alpha}_{i2}=0$
for
${\alpha}_{i1}={\alpha}_{i2}=0$
for
 $1\le i\le J$
$1\le i\le J$
-
• Dimensionality 1: In this case,
 ${\alpha}_{i1}>0$
and
${\alpha}_{i1}>0$
and
 ${\alpha}_{i2}=0$
for
${\alpha}_{i2}=0$
for
 $1\le i\le J$
$1\le i\le J$
-
• Dimensionality 2: In this case,
 ${\alpha}_{i1}>0$
and
${\alpha}_{i1}>0$
and
 ${\alpha}_{i2}=0$
for
${\alpha}_{i2}=0$
for
 $1\le i\le {J}_1$
, and
$1\le i\le {J}_1$
, and
 ${\alpha}_{i2}>0$
and
${\alpha}_{i2}>0$
and
 ${\alpha}_{i1}=0$
for
${\alpha}_{i1}=0$
for
 ${J}_1<i\le {J}_2$
. We used
${J}_1<i\le {J}_2$
. We used
 ${J}_1=\mathrm{ceiling}\left(J/2\right)$
.
${J}_1=\mathrm{ceiling}\left(J/2\right)$
.
The methods discussed allow several ways to obtain a
![]() $p$
-value: based on
$p$
-value: based on
![]() ${C}_{ij+}$
or
${C}_{ij+}$
or
![]() ${Z}_{ij}$
; aggregated with LR, CL, PS, PP, PB, CS, CP, or CB; and their covariance matrix estimated with the sample moments or bootstrapping or set to the identity matrix. We adopt the following convention to name the tests with four-letter acronyms: The first letter indicates the pairwise statistic (Z for the
${Z}_{ij}$
; aggregated with LR, CL, PS, PP, PB, CS, CP, or CB; and their covariance matrix estimated with the sample moments or bootstrapping or set to the identity matrix. We adopt the following convention to name the tests with four-letter acronyms: The first letter indicates the pairwise statistic (Z for the
![]() ${Z}_{ij}$
and M for the MCCs,
${Z}_{ij}$
and M for the MCCs,
![]() ${C}_{ij+}$
); the second letter indicates the covariance matrix (B for bootstrapping, M for moments, I for identity matrix, and N for none); the last two letters indicate the aggregation method (LR, CL, PS, PP, PB, CS, CP, or CB). For example, ZICS is based on
${C}_{ij+}$
); the second letter indicates the covariance matrix (B for bootstrapping, M for moments, I for identity matrix, and N for none); the last two letters indicate the aggregation method (LR, CL, PS, PP, PB, CS, CP, or CB). For example, ZICS is based on
![]() ${Z}_{ij}$
s with the identity matrix and aggregation with the conditionalized sum. An asterisk will be used to indicate a group of tests; for example, ZI** is the group of tests based on the
${Z}_{ij}$
s with the identity matrix and aggregation with the conditionalized sum. An asterisk will be used to indicate a group of tests; for example, ZI** is the group of tests based on the
![]() ${Z}_{ij}$
s with the identity matrix. Not all combinations are reasonable: The identity matrix is only reasonable for the
${Z}_{ij}$
s with the identity matrix. Not all combinations are reasonable: The identity matrix is only reasonable for the
![]() ${Z}_{ij}$
s but not for the
${Z}_{ij}$
s but not for the
![]() ${C}_{ij+}$
s, and the sample moments and bootstrap method make sense only for LR, CL, and PS. The remaining 20 relevant combinations are displayed in the first column of Table 1. In addition to these tests, we studied the DETECT index
${C}_{ij+}$
s, and the sample moments and bootstrap method make sense only for LR, CL, and PS. The remaining 20 relevant combinations are displayed in the first column of Table 1. In addition to these tests, we studied the DETECT index
![]() ${\widehat{D}}_1$
.
${\widehat{D}}_1$
.
Table 1 Rejection rates for various tests, based on 1000 samples with fixed item parameters

Note: M = MCC (
![]() ${C}_{ij+}$
); Z = pairwise Z-statistic (
${C}_{ij+}$
); Z = pairwise Z-statistic (
![]() ${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditional sum; CP = conditional product; CB = conditional Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters were fixed to
${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditional sum; CP = conditional product; CB = conditional Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters were fixed to
![]() ${\alpha}_{id}\in \left\{0,1\right\},{\beta}_i=0$
. Each of the 1000 samples contained 1000 subjects.
${\alpha}_{id}\in \left\{0,1\right\},{\beta}_i=0$
. Each of the 1000 samples contained 1000 subjects.
The simulations were conducted in R, and the code is provided on the Open Science Framework (https://osf.io/hyuzm/). Statistical testing was done at a nominal level of significance
![]() $\alpha =0.05$
. We programmed the CARP tests with the training sample size equal to 30% of the total sample. For DETECT, we used the confirmatory DETECT function conf.detect of the sirt R-package (Robitzsch, Reference Robitzsch2022), with all items in one cluster; this gives
$\alpha =0.05$
. We programmed the CARP tests with the training sample size equal to 30% of the total sample. For DETECT, we used the confirmatory DETECT function conf.detect of the sirt R-package (Robitzsch, Reference Robitzsch2022), with all items in one cluster; this gives
![]() ${\widehat{D}}_1$
. We rejected unidimensionality if
${\widehat{D}}_1$
. We rejected unidimensionality if
![]() ${\widehat{D}}_1>0.20$
, as recommended in the sirt documentation and Roussos and Ozbek (2006, p. 220).
${\widehat{D}}_1>0.20$
, as recommended in the sirt documentation and Roussos and Ozbek (2006, p. 220).
DETECT had a rejection rate of 0 in all circumstances. In the Discussion, we reflect on this result. Tables 1 and 2 show the rejection rates for all other methods. Table 1 shows the rejection rates with all
![]() ${\alpha}_{id}\in \left\{0,1\right\},{\beta}_i=0$
for 1000 samples of 1000 subjects. All 1000 samples in a column are generated with the same parameters. Table 2 shows the rejection rates if the
${\alpha}_{id}\in \left\{0,1\right\},{\beta}_i=0$
for 1000 samples of 1000 subjects. All 1000 samples in a column are generated with the same parameters. Table 2 shows the rejection rates if the
![]() ${\alpha}_{id}$
that are not constrained to be zero have distribution
${\alpha}_{id}$
that are not constrained to be zero have distribution
![]() ${\alpha}_{id}\sim Uniform\left(0,2\right)$
and the
${\alpha}_{id}\sim Uniform\left(0,2\right)$
and the
![]() ${\beta}_i\sim Uniform\left(-2,2\right)$
. The 1000 samples in a column of Table 2 all have different parameters, and all contain 1000 subjects.
${\beta}_i\sim Uniform\left(-2,2\right)$
. The 1000 samples in a column of Table 2 all have different parameters, and all contain 1000 subjects.
Table 2 Rejection rates for various tests, based on 1000 samples with random item parameters

Note: M = MCC (
![]() ${C}_{ij+}$
); Z = pairwise Z-statistic (
${C}_{ij+}$
); Z = pairwise Z-statistic (
![]() ${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditionalized sum; CP = conditionalized product; CB = conditionalized Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters had distribution
${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditionalized sum; CP = conditionalized product; CB = conditionalized Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters had distribution
![]() ${\alpha}_{i1}={\alpha}_{i2}=0$
(dimensionality 0),
${\alpha}_{i1}={\alpha}_{i2}=0$
(dimensionality 0),
![]() ${\alpha}_{i1}\sim Uniform\left(0,2\right)$
,
${\alpha}_{i1}\sim Uniform\left(0,2\right)$
,
![]() ${\alpha}_{i2}=0$
(dimensionality 1), or
${\alpha}_{i2}=0$
(dimensionality 1), or
![]() ${\alpha}_{i1},{\alpha}_{i2}\sim Uniform\left(0,2\right)$
(dimensionality 2), and
${\alpha}_{i1},{\alpha}_{i2}\sim Uniform\left(0,2\right)$
(dimensionality 2), and
![]() ${\beta}_i\sim Uniform\left(-2,2\right)$
. Each of the 1000 samples contained 1000 subjects.
${\beta}_i\sim Uniform\left(-2,2\right)$
. Each of the 1000 samples contained 1000 subjects.
We conclude that only the following combinations keep the Type 1 error rate under control in both dimensionality 0 and dimensionality 1, at least in the above cases:
-
• If the covariance matrix is replaced by the identity matrix: all aggregation methods based on the pairwise
 ${Z}_{ij}$
-statistics.
${Z}_{ij}$
-statistics. -
• If the covariance matrix is estimated from sample moments: all aggregation methods based on pairwise
 ${C}_{ij+}$
or
${C}_{ij+}$
or
 ${Z}_{ij}$
-statistics.
${Z}_{ij}$
-statistics. -
• If the covariance matrix is estimated by bootstrapping: only PS, based on pairwise
 ${C}_{ij+}$
or
${C}_{ij+}$
or
 ${Z}_{ij}$
-statistics.
${Z}_{ij}$
-statistics.
The tests *BCL have a Type I error rate that significantly exceeds 0.05 in Table 1 (p = 0.0006). If we omit these tests, and compare the other tests that use a covariance matrix (CL, LR, and PS) across the different versions (M or Z; bootstrap, moments, or identity), then the tests based on the pairwise
![]() ${Z}_{ij}$
-statistics with the identity matrix have the highest power. The tests where the covariance matrix was based on the sample moments had the lowest power, and we conclude that this method has no advantages.
${Z}_{ij}$
-statistics with the identity matrix have the highest power. The tests where the covariance matrix was based on the sample moments had the lowest power, and we conclude that this method has no advantages.
The maximum discrimination parameter
![]() ${\alpha}_{id}=1.0$
in the simulations of Tables 1 and 2 is rather low. For a broader view, we also conducted simulations with discrimination parameters
${\alpha}_{id}=1.0$
in the simulations of Tables 1 and 2 is rather low. For a broader view, we also conducted simulations with discrimination parameters
![]() ${\alpha}_{id}=1.7$
(medium) and
${\alpha}_{id}=1.7$
(medium) and
![]() ${\alpha}_{id}=7.0$
(extremely high) if the item loads on dimension
${\alpha}_{id}=7.0$
(extremely high) if the item loads on dimension
![]() $d$
, using 100 simulations of 1000 subjects per case. Figure 1 shows the plots of the p-values (Schweder & Spjøtvoll, Reference Schweder and Spjøtvoll1982) for the cases with dimensionality 0 and 1, and Figure 2 shows these plots for dimensionality 2. If the p-values have a uniform distribution, they lay on the diagonal line
$d$
, using 100 simulations of 1000 subjects per case. Figure 1 shows the plots of the p-values (Schweder & Spjøtvoll, Reference Schweder and Spjøtvoll1982) for the cases with dimensionality 0 and 1, and Figure 2 shows these plots for dimensionality 2. If the p-values have a uniform distribution, they lay on the diagonal line
![]() $y=x$
in the plot. These plots confirm the conclusions of Tables 1 and 2: in cases with dimensionality 0 (
$y=x$
in the plot. These plots confirm the conclusions of Tables 1 and 2: in cases with dimensionality 0 (
![]() ${\alpha}_{i1}={\alpha}_{i2}=0$
), all tests produce p-values that are approximately uniformly distributed or slightly higher. In cases with dimensionality 1, (
${\alpha}_{i1}={\alpha}_{i2}=0$
), all tests produce p-values that are approximately uniformly distributed or slightly higher. In cases with dimensionality 1, (
![]() ${\alpha}_{i1}>0,{\alpha}_{i2}=0$
), all tests produce p-values that higher than uniform, and this effect increases with the discrimination parameter. This is to be expected because the population values of the conditional covariances are positive in unidimensional cases with
${\alpha}_{i1}>0,{\alpha}_{i2}=0$
), all tests produce p-values that higher than uniform, and this effect increases with the discrimination parameter. This is to be expected because the population values of the conditional covariances are positive in unidimensional cases with
![]() ${\alpha}_{i1}>0$
. The power is generally lowest if the covariance matrix is estimated with the moments method. With bootstrapping, each Z***-test produces p-values that are very close to the p-values of the corresponding M***-test. However, the power of the tests based on the identity matrix matches or outperforms the power of the corresponding tests based on bootstrapping. The next simulation study will therefore focus on the tests based on the identity matrix.
${\alpha}_{i1}>0$
. The power is generally lowest if the covariance matrix is estimated with the moments method. With bootstrapping, each Z***-test produces p-values that are very close to the p-values of the corresponding M***-test. However, the power of the tests based on the identity matrix matches or outperforms the power of the corresponding tests based on bootstrapping. The next simulation study will therefore focus on the tests based on the identity matrix.

Figure 1 Plots of p-values showing the Type I error rates. Note: The vertical axis is the p-value and the horizontal axis is the rank of the p-value. Dashed curve = M***, solid curve = Z***, black = CT, red = LR, green = PS, blue = CS, light blue = PP, and magenta = CP.

Figure 2 Plots of p-values showing the power. Note: The vertical axis is the p-value and the horizontal axis is the rank of the p-value. Dashed curve = M***, solid curve = Z***, black = CT, red = LR, green = PS, blue = CS, light blue = PP, and magenta = CP.
9 Simulation study II: comparison of aggregation methods
In this second simulation study, we focussed on the tests that use the identity matrix as the covariance matrix of the
![]() $Z$
-statistics. The goal was to determine which aggregation methods (CL, LR, PS, CS, PP, CP, PB, and CB) have the highest power and whether this depends on the number of items, number of subjects, and discrimination parameters. The goal was furthermore to determine whether there are cases with unexpected low power. We investigate the effects of the number of items (
$Z$
-statistics. The goal was to determine which aggregation methods (CL, LR, PS, CS, PP, CP, PB, and CB) have the highest power and whether this depends on the number of items, number of subjects, and discrimination parameters. The goal was furthermore to determine whether there are cases with unexpected low power. We investigate the effects of the number of items (
![]() $J$
), sample size (
$J$
), sample size (
![]() $N$
), and discrimination parameter (
$N$
), and discrimination parameter (
![]() ${\alpha}_{id}$
) on the rejection rates, with fixed item difficulty
${\alpha}_{id}$
) on the rejection rates, with fixed item difficulty
![]() ${\beta}_i=0$
, using 100 simulations per combination. The rejection rates of the two-dimensional cases with low discrimination parameters,
${\beta}_i=0$
, using 100 simulations per combination. The rejection rates of the two-dimensional cases with low discrimination parameters,
![]() ${\alpha}_{id}\in \left\{0,1\right\}$
, are shown in Figure 3.
${\alpha}_{id}\in \left\{0,1\right\}$
, are shown in Figure 3.

Figure 3 Rejection rates as a function of the number of items and sample sizes.
For medium-valued discrimination parameters,
![]() ${\alpha}_{id}\in \left\{0,1.7\right\}$
, the estimated power was generally 0.99 or 1.00 even with
${\alpha}_{id}\in \left\{0,1.7\right\}$
, the estimated power was generally 0.99 or 1.00 even with
![]() $N=500$
and
$N=500$
and
![]() $J=10$
, except for PB and CB. We did not display these excellent power rates in a figure because they do not help discern any pattern. For low discrimination parameters,
$J=10$
, except for PB and CB. We did not display these excellent power rates in a figure because they do not help discern any pattern. For low discrimination parameters,
![]() ${\alpha}_{id}\in \left\{0,1\right\}$
, and
${\alpha}_{id}\in \left\{0,1\right\}$
, and
![]() $N=\mathrm{2,000}$
, the power was usually about .90 or higher, with the exception of ZIPB and ZICB. The power differences between the tests are more pronounced for
$N=\mathrm{2,000}$
, the power was usually about .90 or higher, with the exception of ZIPB and ZICB. The power differences between the tests are more pronounced for
![]() ${\alpha}_{id}\in \left\{0,1\right\}$
and
${\alpha}_{id}\in \left\{0,1\right\}$
and
![]() $N=500$
or
$N=500$
or
![]() $N=1000$
. There we see that the power of ZICL, ZICS, and ZICP increases with the number of items, and that the power of these three tests is generally the highest, except that the power of ZIPP is higher if the number of items is small. The power of ZIPB and ZICB is generally among the lowest and tends to remain low if the number of items increases with
$N=1000$
. There we see that the power of ZICL, ZICS, and ZICP increases with the number of items, and that the power of these three tests is generally the highest, except that the power of ZIPP is higher if the number of items is small. The power of ZIPB and ZICB is generally among the lowest and tends to remain low if the number of items increases with
![]() $N=500$
or
$N=500$
or
![]() $N=1000$
. The power of ZIPS tends to decrease with the number of items if
$N=1000$
. The power of ZIPS tends to decrease with the number of items if
![]() $N=500$
or
$N=500$
or
![]() $N=1000$
. The power of ZILR tends to remain low if the number of items increases with
$N=1000$
. The power of ZILR tends to remain low if the number of items increases with
![]() $N=500$
, but slowly increases if
$N=500$
, but slowly increases if
![]() $N=1000$
. In sum, the highest power is observed for ZICL, ZICS, ZICP, and sometimes ZIPP. Therefore, we will focus on these tests in the next section.
$N=1000$
. In sum, the highest power is observed for ZICL, ZICS, ZICP, and sometimes ZIPP. Therefore, we will focus on these tests in the next section.
10 Simulation study III: type I error rates
In Simulation Study I, we investigated the Type I error rate only for
![]() $J=10$
items and a sample size of
$J=10$
items and a sample size of
![]() $N=1000$
subjects. The present section discusses the Type I error rate more thoroughly, with simulations with varying
$N=1000$
subjects. The present section discusses the Type I error rate more thoroughly, with simulations with varying
![]() $J$
and
$J$
and
![]() $N$
, but only for the ZI** tests, which were selected in Simulation Study I, and we focus especially on the tests ZICL, ZICS, ZICP, and ZIPP, based on their power in Simulation Study II. We label tests with
$N$
, but only for the ZI** tests, which were selected in Simulation Study I, and we focus especially on the tests ZICL, ZICS, ZICP, and ZIPP, based on their power in Simulation Study II. We label tests with
![]() $J\le 10$
small and tests with
$J\le 10$
small and tests with
![]() $J>10$
large. Further, we consider
$J>10$
large. Further, we consider
![]() $N\le 1000$
small and
$N\le 1000$
small and
![]() $N>1000$
large.
$N>1000$
large.
10.1 Zero-dimensional cases
We investigated the effects of the number of items (
![]() $J$
), sample sizes (
$J$
), sample sizes (
![]() $N$
) on the rejection rates for a nominal significance level of 5%, with fixed discrimination parameters
$N$
) on the rejection rates for a nominal significance level of 5%, with fixed discrimination parameters
![]() ${\alpha}_{id}=0$
and fixed item difficulties
${\alpha}_{id}=0$
and fixed item difficulties
![]() ${\beta}_i=0$
, using 100 simulations per combination. For the number of items, we used all small values
${\beta}_i=0$
, using 100 simulations per combination. For the number of items, we used all small values
![]() $\left(J=3,4,5,6,7,8,9,10\right)$
and two large values (
$\left(J=3,4,5,6,7,8,9,10\right)$
and two large values (
![]() $J=20,30$
). For the number of subjects, we used several small values
$J=20,30$
). For the number of subjects, we used several small values
![]() $(N=250,500,750,1000)$
and two large values (
$(N=250,500,750,1000)$
and two large values (
![]() $N=2000,N={10}^4$
). For each of the test statistics ZICL, ZICS, ZICP, and ZIPP, the cumulative distribution of rejection counts was larger than the cumulative binomial distribution with
$N=2000,N={10}^4$
). For each of the test statistics ZICL, ZICS, ZICP, and ZIPP, the cumulative distribution of rejection counts was larger than the cumulative binomial distribution with
![]() $n=100,\pi =0.05$
; that is, the rejection rates were smaller than expected under the binomial distribution. The highest rejection rates (0.07, 0.08, 0.09, and 0.10) were mostly observed with
$n=100,\pi =0.05$
; that is, the rejection rates were smaller than expected under the binomial distribution. The highest rejection rates (0.07, 0.08, 0.09, and 0.10) were mostly observed with
![]() $J=3,4,5,6$
and
$J=3,4,5,6$
and
![]() $N={10}^4$
. Therefore a second simulation was conducted with these values of
$N={10}^4$
. Therefore a second simulation was conducted with these values of
![]() $J$
and
$J$
and
![]() $N$
, but with 1000 simulations per combination. The rejection rates for ZICL, ZICS, ZICP, and ZIPP varied between 0.041 and 0.061, and none were significantly greater than 0.05. We also studied this for cases where the
$N$
, but with 1000 simulations per combination. The rejection rates for ZICL, ZICS, ZICP, and ZIPP varied between 0.041 and 0.061, and none were significantly greater than 0.05. We also studied this for cases where the
![]() $J,N,{\alpha}_{id},{\beta}_i$
were chosen randomly and independently from uniform distributions with
$J,N,{\alpha}_{id},{\beta}_i$
were chosen randomly and independently from uniform distributions with
![]() $J$
between 3 and 30,
$J$
between 3 and 30,
![]() $N$
between 250 and
$N$
between 250 and
![]() ${10}^4$
, and
${10}^4$
, and
![]() ${\beta}_i\in \left(-2,2\right)$
. We sampled 100 cases of
${\beta}_i\in \left(-2,2\right)$
. We sampled 100 cases of
![]() $\left(J,N,\boldsymbol{\beta} \right)$
, and generated 100 data sets with a zero-dimensional model for each case. The cumulative distribution of rejection counts was larger than the cumulative binomial distribution with
$\left(J,N,\boldsymbol{\beta} \right)$
, and generated 100 data sets with a zero-dimensional model for each case. The cumulative distribution of rejection counts was larger than the cumulative binomial distribution with
![]() $n=100,\pi =0.05$
for all ZI** tests except ZIPB. ZIPB had two cases with rejection rates of 0.11. We conclude that the Type I error rate is under control for the tests ZICL, ZICS, ZICP, and ZIPP in these cases.
$n=100,\pi =0.05$
for all ZI** tests except ZIPB. ZIPB had two cases with rejection rates of 0.11. We conclude that the Type I error rate is under control for the tests ZICL, ZICS, ZICP, and ZIPP in these cases.
10.2 Unidimensional cases
We investigated the effects of the number of items (
![]() $J$
), sample sizes (
$J$
), sample sizes (
![]() $N$
) on the rejection rates for a nominal significance level of 5%, with fixed discrimination parameters
$N$
) on the rejection rates for a nominal significance level of 5%, with fixed discrimination parameters
![]() ${\alpha}_{i1}=1,{\alpha}_{i2}=0$
and fixed item difficulties
${\alpha}_{i1}=1,{\alpha}_{i2}=0$
and fixed item difficulties
![]() ${\beta}_i=0$
, using 100 simulations per combination. For the number of items, we used all small values
${\beta}_i=0$
, using 100 simulations per combination. For the number of items, we used all small values
![]() $\left(J=3,4,5,6,7,8,9,10\right)$
and two large values (
$\left(J=3,4,5,6,7,8,9,10\right)$
and two large values (
![]() $J=20,30$
). For the number of subjects, we used several small values (
$J=20,30$
). For the number of subjects, we used several small values (
![]() $N=250,500,750,1000)$
and two large values (
$N=250,500,750,1000)$
and two large values (
![]() $N=2000,N={10}^4$
). The highest rejection rate was 0.01. We also studied this for cases where the
$N=2000,N={10}^4$
). The highest rejection rate was 0.01. We also studied this for cases where the
![]() $J,N,{\alpha}_{i1},{\beta}_i$
were chosen randomly and independently from uniform distributions with
$J,N,{\alpha}_{i1},{\beta}_i$
were chosen randomly and independently from uniform distributions with
![]() $J$
between 3 and 30,
$J$
between 3 and 30,
![]() $N$
between 250 and
$N$
between 250 and
![]() ${10}^4$
,
${10}^4$
,
![]() ${\alpha}_{i1}\in \left(0,2\right)$
, and
${\alpha}_{i1}\in \left(0,2\right)$
, and
![]() ${\beta}_i\in \left(-2,2\right)$
. We sampled 100 cases of
${\beta}_i\in \left(-2,2\right)$
. We sampled 100 cases of
![]() $\left(J,N,\boldsymbol{\beta} \right)$
, and generated 100 data sets with a unidimensional model for each case. The rejection rates are given in the first nine rows of Table 3. The rejection rates of ZICP, ZICL, ZICS, and ZIPP were at most 0.04. The cumulative distribution of rejection counts of each of the tests was larger than the cumulative binomial distribution with
$\left(J,N,\boldsymbol{\beta} \right)$
, and generated 100 data sets with a unidimensional model for each case. The rejection rates are given in the first nine rows of Table 3. The rejection rates of ZICP, ZICL, ZICS, and ZIPP were at most 0.04. The cumulative distribution of rejection counts of each of the tests was larger than the cumulative binomial distribution with
![]() $n=100,\pi =0.05$
, that is, the rejection rates were smaller than expected under the binomial distribution. Table 3 also shows the rejection rates in various other settings of
$n=100,\pi =0.05$
, that is, the rejection rates were smaller than expected under the binomial distribution. Table 3 also shows the rejection rates in various other settings of
![]() $J$
and
$J$
and
![]() $N$
, with similar conclusions.
$N$
, with similar conclusions.
Table 3
Distribution of rejection rates in various settings of
![]() $J$
and
$J$
and
![]() $N$
with unidimensional models
$N$
with unidimensional models

Note: In each setting of
![]() $J$
and
$J$
and
![]() $N$
, 100 parameter cases were generated with
$N$
, 100 parameter cases were generated with
![]() $J\sim Uniform\left(\mathit{min}\ J,\mathit{max}\ J\right)$
,
$J\sim Uniform\left(\mathit{min}\ J,\mathit{max}\ J\right)$
,
![]() $N\sim Uniform\left(\mathit{min}\ N,\mathit{max}\ N\right)$
,
$N\sim Uniform\left(\mathit{min}\ N,\mathit{max}\ N\right)$
,
![]() ${\alpha}_{i1}\sim Uniform\left(0,2\right)$
,
${\alpha}_{i1}\sim Uniform\left(0,2\right)$
,
![]() ${\alpha}_{i2}=0$
, and
${\alpha}_{i2}=0$
, and
![]() ${\beta}_i\sim Uniform\left(-2,2\right)$
. In each of these 100 parameter cases, 100 samples were simulated. Each cell shows the number of parameter cases with the rejection rate specified in that row. For example, for ZICP, there were 18 cases out of 100 that had a rejection rate of 0.01 over 100 samples in the first setting.
${\beta}_i\sim Uniform\left(-2,2\right)$
. In each of these 100 parameter cases, 100 samples were simulated. Each cell shows the number of parameter cases with the rejection rate specified in that row. For example, for ZICP, there were 18 cases out of 100 that had a rejection rate of 0.01 over 100 samples in the first setting.
11 Simulation study IV: without continuity correction
The previous simulations were conducted with the
![]() ${Z}_{ij}$
-statistics corrected for continuity with the addition of a term 0.5 in the numerator, as proposed by Rosenbaum (Reference Rosenbaum1984) and adopted by Ellis and Sijtsma (Reference Ellis and Sijtsma2023). Many other continuity corrections exist (Andrés et al., Reference Andrés, Hernández and Moreno2024), and we are not sure that a continuity correction is necessary for the sample sizes ordinarily found in IRT. Therefore, we repeated the simulation studies of the ZI-statistics without continuity correction. The simulations of Table 1 and Table 2 are repeated in Table 4 and Table 5 without continuity correction.
${Z}_{ij}$
-statistics corrected for continuity with the addition of a term 0.5 in the numerator, as proposed by Rosenbaum (Reference Rosenbaum1984) and adopted by Ellis and Sijtsma (Reference Ellis and Sijtsma2023). Many other continuity corrections exist (Andrés et al., Reference Andrés, Hernández and Moreno2024), and we are not sure that a continuity correction is necessary for the sample sizes ordinarily found in IRT. Therefore, we repeated the simulation studies of the ZI-statistics without continuity correction. The simulations of Table 1 and Table 2 are repeated in Table 4 and Table 5 without continuity correction.
Table 4 Rejection rates for various tests without continuity correction with fixed item parameters

Note: Z = pairwise Z-statistic (
![]() ${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditional sum; CP = conditional product; CB = conditional Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters were fixed to
${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditional sum; CP = conditional product; CB = conditional Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters were fixed to
![]() ${\alpha}_{id}\in \left\{0,1\right\},{\beta}_i=0$
. Each rate is based on 1000 samples of 1000 subjects.
${\alpha}_{id}\in \left\{0,1\right\},{\beta}_i=0$
. Each rate is based on 1000 samples of 1000 subjects.
Table 5 Rejection rates for various tests without continuity correction with random item parameters

Note: Z = pairwise Z-statistic (
![]() ${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditionalized sum; CP = conditionalized product; CB = conditionalized Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters had distribution
${Z}_{ij}$
); LR = likelihood ratio; CL = conditional likelihood ratio; CS = conditionalized sum; CP = conditionalized product; CB = conditionalized Bonferroni; PS = preselected sum; PP = preselected product; and PB = preselected Bonferroni. The item parameters had distribution
![]() ${\alpha}_{i1}={\alpha}_{i2}=0$
(dimensionality 0),
${\alpha}_{i1}={\alpha}_{i2}=0$
(dimensionality 0),
![]() ${\alpha}_{i1}\sim Uniform\left(0,2\right)$
,
${\alpha}_{i1}\sim Uniform\left(0,2\right)$
,
![]() ${\alpha}_{i2}=0$
(dimensionality 1), or
${\alpha}_{i2}=0$
(dimensionality 1), or
![]() ${\alpha}_{i1},{\alpha}_{i2}\sim Uniform\left(0,2\right)$
(dimensionality 2), and
${\alpha}_{i1},{\alpha}_{i2}\sim Uniform\left(0,2\right)$
(dimensionality 2), and
![]() ${\beta}_i\sim Uniform\left(-2,2\right)$
. Each rate is based on 1000 samples of 1000 subjects.
${\beta}_i\sim Uniform\left(-2,2\right)$
. Each rate is based on 1000 samples of 1000 subjects.
As was to be expected, the rejection rates were now generally larger than in Tables 1 and 2. In Table 4, most Type I error rates (Dimensionality 0) were now 0.05 or slightly higher, and the power (Dimensionality 2) was substantially higher than in Table 1. In Table 5, all Type I error rates are below 0.05, and the power is still larger than in Table 2. The power rates in Tables 4 and 5 are low, but note that these results were obtained for low discrimination parameters (
![]() ${\alpha}_{id}\le 1$
). We also repeated Simulation Study III without continuity correction, and our conclusion is that the rejection rates were dominated by a binomial distribution with probability 0.05 in all cases, meaning that the Type I error rate is under control. The rejection rates of these versions of ZICL, ZICP, and ZICS are close to 0.05 in the zero-dimensional cases.
${\alpha}_{id}\le 1$
). We also repeated Simulation Study III without continuity correction, and our conclusion is that the rejection rates were dominated by a binomial distribution with probability 0.05 in all cases, meaning that the Type I error rate is under control. The rejection rates of these versions of ZICL, ZICP, and ZICS are close to 0.05 in the zero-dimensional cases.
Table 6 shows the power rates for the simulations underlying Figure 3, but now repeated without continuity correction, with the positive discrimination parameters set to 1 (low). If the objective is to have power > 0.90, then all four tests achieved this goal with
![]() $N=2000$
and
$N=2000$
and
![]() $J\ge 10$
, and also with
$J\ge 10$
, and also with
![]() $N=1000$
and
$N=1000$
and
![]() $J\ge 14$
, but not with
$J\ge 14$
, but not with
![]() $N=500$
. However, if the positive discrimination parameters are equal to 1.7 (medium), then the power rates were 1.00 even with
$N=500$
. However, if the positive discrimination parameters are equal to 1.7 (medium), then the power rates were 1.00 even with
![]() $N=500$
and
$N=500$
and
![]() $J\ge 10$
. We did not display these excellent power rates in a table because they were all 1.00.
$J\ge 10$
. We did not display these excellent power rates in a table because they were all 1.00.
Table 6 Rejection rates for various tests without continuity correction with low discrimination parameters

Note: Z = pairwise Z-statistic (
![]() ${Z}_{ij}$
); CL = conditional likelihood ratio; CS = conditional sum; CP = conditional product; and PP = preselected product. The item parameters were fixed to
${Z}_{ij}$
); CL = conditional likelihood ratio; CS = conditional sum; CP = conditional product; and PP = preselected product. The item parameters were fixed to
![]() ${\alpha}_{id}\in \{0,1\},\ {\beta}_i=0$
. Each rate is based on 100 samples.
${\alpha}_{id}\in \{0,1\},\ {\beta}_i=0$
. Each rate is based on 100 samples.
12 Conclusions and discussion
We conclude that the pairwise CARP tests Ellis and Sijtsma (Reference Ellis and Sijtsma2023) proposed can best be aggregated with four of the tests developed here: ZICL, ZICP, ZICS, and ZIPP. These tests control the Type I error rate in a wide variety of test lengths and sample sizes, and their power against two-dimensional alternatives is larger than the power of other aggregate statistics that we studied. ZIPP had the greatest relative power if there were less than 18 items with
![]() $N=1000$
, but not in most other cases. Further investigations are needed to determine whether this is also true for alternatives with more than two dimensions.
$N=1000$
, but not in most other cases. Further investigations are needed to determine whether this is also true for alternatives with more than two dimensions.
The Type I error rates of the ZI-tests are well below the nominal rate of 0.05, and this suggests that improvement is possible. The pairwise Z-statistic, as defined by Ellis and Sijtsma (Reference Ellis and Sijtsma2023), includes a continuity correction that might be too conservative. Based on our simulations, we conclude that the continuity correction may be abandoned for the sample sizes we studied (
![]() $N\ge 500$
). Without continuity correction, the Type I error rate is still under control, and the power increases. The Type I error rates of ZICL, ZICP, and ZICS are then close to 0.05 in the zero-dimensional cases of Tables 4 and 5.
$N\ge 500$
). Without continuity correction, the Type I error rate is still under control, and the power increases. The Type I error rates of ZICL, ZICP, and ZICS are then close to 0.05 in the zero-dimensional cases of Tables 4 and 5.
The Type I error rate in unidimensional cases is far below 0.05, even without continuity correction, but this does not imply that the tests are too conservative. As an analogy, consider the elementary normal-theory one-sided Z-test for a mean
![]() $\mu$
with known variance
$\mu$
with known variance
![]() ${\sigma}^2$
. For the null hypothesis
${\sigma}^2$
. For the null hypothesis
![]() $\mu \ge 0$
and sample mean
$\mu \ge 0$
and sample mean
![]() $\overline{X}$
one would use
$\overline{X}$
one would use
![]() $Z=\left(\overline{X}/\sigma \right)\sqrt{N}$
and reject the null hypothesis if
$Z=\left(\overline{X}/\sigma \right)\sqrt{N}$
and reject the null hypothesis if
![]() $\Phi (Z)<\alpha$
. If real data were generated with
$\Phi (Z)<\alpha$
. If real data were generated with
![]() $\mu >0$
, then
$\mu >0$
, then
![]() $P\left(\Phi (Z)<\alpha \right)<\alpha$
, meaning that the Type I error rate is less than
$P\left(\Phi (Z)<\alpha \right)<\alpha$
, meaning that the Type I error rate is less than
![]() $\alpha$
. This is usually not viewed as a sign that something is wrong with the one-sided Z-test. The situation in our case is similar because we have a one-sided test for a mean, but in our case it is a mean of conditional covariances. In the unidimensional case, this mean is positive, which reduces the Type I error rate.
$\alpha$
. This is usually not viewed as a sign that something is wrong with the one-sided Z-test. The situation in our case is similar because we have a one-sided test for a mean, but in our case it is a mean of conditional covariances. In the unidimensional case, this mean is positive, which reduces the Type I error rate.
If the discrimination parameters equal 1 and the intercepts equal 0, the power rates of ZICL, ZICP, ZICS, and ZIPP are well above 0.90 for
![]() $N=2000$
, regardless of whether the continuity correction is used. For these item parameters, if there are at least 14 items and the continuity correction is abandoned, the power is also above 0.90 for
$N=2000$
, regardless of whether the continuity correction is used. For these item parameters, if there are at least 14 items and the continuity correction is abandoned, the power is also above 0.90 for
![]() $N=1000$
, but the power is substantially below 0.90 for
$N=1000$
, but the power is substantially below 0.90 for
![]() $N=500$
for all studied test lengths between
$N=500$
for all studied test lengths between
![]() $J=10$
and
$J=10$
and
![]() $J=30$
. We emphasize that these power rates were obtained for low discrimination parameters. We consider discrimination parameters of 1 as low because we did not use the general factor 1.7 in our parametrization (unlike e.g., Roussos & Ozbek, Reference Roussos and Ozbek2006). If the positive discrimination parameters equal 1.7 (medium), then the power rates of ZICL, ZICP, ZICS, and ZIPP are 1.00, even with
$J=30$
. We emphasize that these power rates were obtained for low discrimination parameters. We consider discrimination parameters of 1 as low because we did not use the general factor 1.7 in our parametrization (unlike e.g., Roussos & Ozbek, Reference Roussos and Ozbek2006). If the positive discrimination parameters equal 1.7 (medium), then the power rates of ZICL, ZICP, ZICS, and ZIPP are 1.00, even with
![]() $N=500$
and all investigated test lengths from 10 to 30, based on simulations using 100 samples.
$N=500$
and all investigated test lengths from 10 to 30, based on simulations using 100 samples.
We also compared our statistics with the DETECT index, applied in a confirmatory manner, using the criterion
![]() ${D}_1<0.20$
. To our surprise, despite the theoretical similarity of this index to the ZIPS statistic, this index appeared to lack discriminatory power, as it never rejected the hypothesis of unidimensionality. This is a puzzling result, seemingly at odds with the positive evaluations reported by the index’s creators. While we have concerns about the validity of our results for DETECT, we were unable to identify any errors in our code. We believe this issue warrants further investigation.
${D}_1<0.20$
. To our surprise, despite the theoretical similarity of this index to the ZIPS statistic, this index appeared to lack discriminatory power, as it never rejected the hypothesis of unidimensionality. This is a puzzling result, seemingly at odds with the positive evaluations reported by the index’s creators. While we have concerns about the validity of our results for DETECT, we were unable to identify any errors in our code. We believe this issue warrants further investigation.
Our study provides three new statistics for a confirmatory test of unidimensionality in monotone IRT models, and they seem to outperform older methods—at least in the cases we simulated. Still, the power of these methods is somewhat disappointing for sample size
![]() $N=1000$
and discrimination parameter 1, and better methods may be possible. A simple improvement might be found in the size of the training sample, which was set at 30% in all our analyses. Furthermore, aggregation of different splits into training samples and test samples might be useful. Finally, it would be worthwhile to investigate which of the four tests can be recommended as most powerful under various circumstances.
$N=1000$
and discrimination parameter 1, and better methods may be possible. A simple improvement might be found in the size of the training sample, which was set at 30% in all our analyses. Furthermore, aggregation of different splits into training samples and test samples might be useful. Finally, it would be worthwhile to investigate which of the four tests can be recommended as most powerful under various circumstances.
Data availability statement
The simulated data and the code that generated it, are available in the Open Science Framework repository at https://osf.io/hyuzm/
A Appendix
Proposition A1. If
![]() $Z$
is independent of
$Z$
is independent of
![]() $\left(X,Y\right)$
then
$\left(X,Y\right)$
then
![]() $Cov\left(X, YZ\right)= Cov\left(X,Y\right)\mathbb{E}(Z)$
.
$Cov\left(X, YZ\right)= Cov\left(X,Y\right)\mathbb{E}(Z)$
.
Proof.
![]() $Cov\left(X, YZ\right)=\mathbb{E}\left( XY Z\right)-\mathbb{E}(X)\mathbb{E}(YZ)=\mathbb{E}(XY)\mathbb{E}(Z)-\mathbb{E}(X)\mathbb{E}(Y)\mathbb{E}(Z)= Cov\left(X,Y\right)\mathbb{E}(Z).$
$Cov\left(X, YZ\right)=\mathbb{E}\left( XY Z\right)-\mathbb{E}(X)\mathbb{E}(YZ)=\mathbb{E}(XY)\mathbb{E}(Z)-\mathbb{E}(X)\mathbb{E}(Y)\mathbb{E}(Z)= Cov\left(X,Y\right)\mathbb{E}(Z).$
A1 The covariance of two sample covariances
In asymptotic distribution free (ADF) SEM, it is common to obtain the covariance matrix of sample covariances as the sample grows to infinity, which is called the asymptotic covariance matrix (e.g., Browne, Reference Browne1984). However, it is also possible to obtain an exact formula for the covariance of two sample covariances for finite
![]() $N$
, provided that the variables have finite fourth moments.
$N$
, provided that the variables have finite fourth moments.
We develop the covariance of two sample covariances, assuming finite fourth moments of the involved variables. Denote the variables to be studied as
![]() $\boldsymbol{X}=\left({X}_1,{X}_2,\dots, {X}_J\right)$
. Suppose that a random sample of
$\boldsymbol{X}=\left({X}_1,{X}_2,\dots, {X}_J\right)$
. Suppose that a random sample of
![]() $N$
subjects is drawn, and denote the score of subject
$N$
subjects is drawn, and denote the score of subject
![]() $n$
on variable
$n$
on variable
![]() $i$
as
$i$
as
![]() ${X}_i^{(n)}$
, and let
${X}_i^{(n)}$
, and let
![]() ${\boldsymbol{X}}^{(n)}=\left({X}_1^{(n)},\dots, {X}_J^{(n)}\right)$
, the score pattern of subject
${\boldsymbol{X}}^{(n)}=\left({X}_1^{(n)},\dots, {X}_J^{(n)}\right)$
, the score pattern of subject
![]() $n$
. We assume that the
$n$
. We assume that the
![]() $N$
subjects are drawn independently, and that therefore their score patterns
$N$
subjects are drawn independently, and that therefore their score patterns
![]() ${\boldsymbol{X}}^{(1)},{\boldsymbol{X}}^{(2)},\dots, {\boldsymbol{X}}^{(N)}$
are independent, and that each
${\boldsymbol{X}}^{(1)},{\boldsymbol{X}}^{(2)},\dots, {\boldsymbol{X}}^{(N)}$
are independent, and that each
![]() ${\boldsymbol{X}}^{(n)}$
has the same multivariate distribution as
${\boldsymbol{X}}^{(n)}$
has the same multivariate distribution as
![]() $\boldsymbol{X}$
. Thus, the
$\boldsymbol{X}$
. Thus, the
![]() ${\boldsymbol{X}}^{(n)}$
are independent copies of
${\boldsymbol{X}}^{(n)}$
are independent copies of
![]() $\boldsymbol{X}$
. We study two sample covariances, given by
$\boldsymbol{X}$
. We study two sample covariances, given by
 $$\begin{align*}{C}_{ij}^N=\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}}{N}\end{align*}$$
$$\begin{align*}{C}_{ij}^N=\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}}{N}\end{align*}$$
 $$\begin{align*}{C}_{kl}^N=\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_k^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_l^{(n)}}{N}\end{align*}$$
$$\begin{align*}{C}_{kl}^N=\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_k^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_l^{(n)}}{N}\end{align*}$$
Using the summation rules for covariances, the covariance of these sample covariances is
 $$\begin{align*}Cov\left({C}_{ij}^N,{C}_{kl}^N\right)= Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}}{N},\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_k^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_l^{(n)}}{N}\right)=\end{align*}$$
$$\begin{align*}Cov\left({C}_{ij}^N,{C}_{kl}^N\right)= Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}}{N},\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}}{N}-\frac{\sum \limits_{n=1}^N{X}_k^{(n)}}{N}\frac{\sum \limits_{n=1}^N{X}_l^{(n)}}{N}\right)=\end{align*}$$
 $$\begin{align*}&{N}^{-2} Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}\right)-{N}^{-3} Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)\\&\quad-{N}^{-3} Cov\left(\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)},\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)}\right)+{N}^{-4} Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right).\end{align*}$$
$$\begin{align*}&{N}^{-2} Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}\right)-{N}^{-3} Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)\\&\quad-{N}^{-3} Cov\left(\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)},\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)}\right)+{N}^{-4} Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right).\end{align*}$$
We will now develop the four terms in this sum, which will be called the four main terms. For the first main term, we need
 $$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}\right)=\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right).\end{align*}$$
$$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}\right)=\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right).\end{align*}$$
This sum has
![]() ${N}^2$
terms, but if
${N}^2$
terms, but if
![]() $n\ne m$
then
$n\ne m$
then
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)=0$
, and in the remaining
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)=0$
, and in the remaining
![]() $N$
terms with
$N$
terms with
![]() $n=m$
,
$n=m$
,
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)= Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(n)}{X}_l^{(n)}\right)= Cov\left({X}_i{X}_j,{X}_k{X}_l\right)$
. Therefore, we obtain
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)= Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(n)}{X}_l^{(n)}\right)= Cov\left({X}_i{X}_j,{X}_k{X}_l\right)$
. Therefore, we obtain
 $$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}\right)=\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)= NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\end{align*}$$
$$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}\right)=\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)= NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\end{align*}$$
For the second main term, we need
 $$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)=\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right).\end{align*}$$
$$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)=\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right).\end{align*}$$
Similar to the previous term, the outcome of the generic covariance term in this sum,
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
, depends on which of the indices
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
, depends on which of the indices
![]() $n,m, and\;r$
are equal. To keep track of this, we constructed Table A1, in which all possible truth values of the equalities
$n,m, and\;r$
are equal. To keep track of this, we constructed Table A1, in which all possible truth values of the equalities
![]() $n=m$
,
$n=m$
,
![]() $n=r$
, and
$n=r$
, and
![]() $m=r$
are listed. Each row contains one combination of truth values and the number of terms with that combination. Each row also contains the intermediate expression of the covariance, where the true equalities of that row are substituted in the generic expression
$m=r$
are listed. Each row contains one combination of truth values and the number of terms with that combination. Each row also contains the intermediate expression of the covariance, where the true equalities of that row are substituted in the generic expression
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
, and the final expression, where this is intermediate expression is rewritten in terms of the central moments of
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
, and the final expression, where this is intermediate expression is rewritten in terms of the central moments of
![]() $\boldsymbol{X}$
. A few examples may clarify this:
$\boldsymbol{X}$
. A few examples may clarify this:
In the second row, we consider the generic terms
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
with
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
with
![]() $n\ne m,n\ne r,m=r$
. There are
$n\ne m,n\ne r,m=r$
. There are
![]() $N\left(N-1\right)$
such terms, and substitution of the equality
$N\left(N-1\right)$
such terms, and substitution of the equality
![]() $m=r$
leads to the intermediate expression
$m=r$
leads to the intermediate expression
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)$
. Since
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(m)}\right)$
. Since
![]() $n\ne m$
,
$n\ne m$
,
![]() ${X}_i^{(n)}{X}_j^{(n)}$
is independent of
${X}_i^{(n)}{X}_j^{(n)}$
is independent of
![]() ${X}_k^{(m)}{X}_l^{(m)}$
, and therefore this covariance is 0, which is the final expression.
${X}_k^{(m)}{X}_l^{(m)}$
, and therefore this covariance is 0, which is the final expression.
In the third row, we consider the generic terms
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
with
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
with
![]() $n\ne m,n=r,m\ne r$
. There are
$n\ne m,n=r,m\ne r$
. There are
![]() $N\left(N-1\right)$
such terms, and substitution of the equality
$N\left(N-1\right)$
such terms, and substitution of the equality
![]() $n=r$
leads to
$n=r$
leads to
![]() $Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(n)}\right)$
. Since
$Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(n)}\right)$
. Since
![]() $n\ne m$
,
$n\ne m$
,
![]() ${X}_i^{(n)}{X}_j^{(n)}$
is independent of
${X}_i^{(n)}{X}_j^{(n)}$
is independent of
![]() ${X}_k^{(m)}$
but not of
${X}_k^{(m)}$
but not of
![]() ${X}_l^{(n)}$
. Here, we can use proposition A1, and obtain
${X}_l^{(n)}$
. Here, we can use proposition A1, and obtain
![]() $Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)$
.
$Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)$
.
In the fourth row, we consider the terms with
![]() $n\ne m,n=r,m=r$
. This is a logical contradiction, and therefore there are 0 of such terms.
$n\ne m,n=r,m=r$
. This is a logical contradiction, and therefore there are 0 of such terms.
Table A1
Development of the term
![]() $\sum_{n=1}^N\sum _{m=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$
$\sum_{n=1}^N\sum _{m=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)},{X}_k^{(m)}{X}_l^{(r)}\right)$

Summarizing from Table A1, we obtain
 $$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)&=N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)\\&\quad+N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_k\right)\mathbb{E}\left({X}_l\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right).\end{align*}$$
$$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)&=N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)\\&\quad+N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_k\right)\mathbb{E}\left({X}_l\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right).\end{align*}$$
For the third main term, we obtain analogously,
 $$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)},\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)}\right)&=N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_j\right)\mathbb{E}\left({X}_i\right)\\&\quad+N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_i\right)\mathbb{E}\left({X}_j\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right).\end{align*}$$
$$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)},\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)}\right)&=N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_j\right)\mathbb{E}\left({X}_i\right)\\&\quad+N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_i\right)\mathbb{E}\left({X}_j\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right).\end{align*}$$
For the fourth term, we need to develop
 $$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)&= Cov\left(\sum \limits_{n=1}^N\sum \limits_{m=1}^N{X}_i^{(n)}{X}_j^{(m)},\sum \limits_{q=1}^N\sum \limits_{r=1}^N{X}_k^{(q)}{X}_l^{(r)}\right)\\&=\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{q=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right).\end{align*}$$
$$\begin{align*}Cov\left(\sum \limits_{n=1}^N{X}_i^{(n)}\sum \limits_{n=1}^N{X}_j^{(n)},\sum \limits_{n=1}^N{X}_k^{(n)}\sum \limits_{n=1}^N{X}_l^{(n)}\right)&= Cov\left(\sum \limits_{n=1}^N\sum \limits_{m=1}^N{X}_i^{(n)}{X}_j^{(m)},\sum \limits_{q=1}^N\sum \limits_{r=1}^N{X}_k^{(q)}{X}_l^{(r)}\right)\\&=\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{q=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right).\end{align*}$$
The generic expression for the covariances in this sum is
![]() $Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right)$
. There are now four indices,
$Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right)$
. There are now four indices,
![]() $n,m,q,\; and\;r$
and therefore there are six equalities that may or may not be true:
$n,m,q,\; and\;r$
and therefore there are six equalities that may or may not be true:
![]() $m=n,q=n,q=m,r=n,r=m,\; and\;r=q.$
All possible truth values of these equalities are listed in Table A2, together with their count, the intermediate expression, and the final expression. For example, in the third row, we consider the case where
$m=n,q=n,q=m,r=n,r=m,\; and\;r=q.$
All possible truth values of these equalities are listed in Table A2, together with their count, the intermediate expression, and the final expression. For example, in the third row, we consider the case where
![]() $r=m$
, while all other indices are unequal. There are
$r=m$
, while all other indices are unequal. There are
![]() $N\left(N-1\right)\left(N-2\right)$
such terms. Substitution of
$N\left(N-1\right)\left(N-2\right)$
such terms. Substitution of
![]() $r=m$
leads to
$r=m$
leads to
![]() $Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right)= Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(m)}{X}_l^{(r)}\right)$
, and then proposition A1 leads to
$Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right)= Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(m)}{X}_l^{(r)}\right)$
, and then proposition A1 leads to
![]() $Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(m)}{X}_l^{(r)}\right)=\mathbb{E}\left({X}_i^{(n)}\right) Cov\left({X}_j^{(m)},{X}_k^{(m)}\right)\mathbb{E}\left({X}_l^{(r)}\right)= Cov\left({X}_j,{X}_l\right)\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_k\right)$
. In row 13 of Table A2, we used the following reasoning:
$Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(m)}{X}_l^{(r)}\right)=\mathbb{E}\left({X}_i^{(n)}\right) Cov\left({X}_j^{(m)},{X}_k^{(m)}\right)\mathbb{E}\left({X}_l^{(r)}\right)= Cov\left({X}_j,{X}_l\right)\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_k\right)$
. In row 13 of Table A2, we used the following reasoning:
A similar argument leads to the final expression in row 19 of Table A2.
Table A2
Development of the term
![]() $\sum_{n=1}^N\sum _{m=1}^N\sum _{q=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right)$
$\sum_{n=1}^N\sum _{m=1}^N\sum _{q=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(m)},{X}_k^{(q)}{X}_l^{(r)}\right)$

Taking all four main terms together, we obtain:
 $$\begin{align*}Cov\left({C}_{ij}^N,{C}_{kl}^N\right)&={N}^{-2}\; NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\\&\quad-{N}^{-3}\left(N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)+N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_k\right)\mathbb{E}\left({X}_l\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\right)\\&\quad-{N}^{-3}\left(N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_j\right)\mathbb{E}\left({X}_i\right)+N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_i\right)\mathbb{E}\left({X}_j\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\right)+\end{align*}$$
$$\begin{align*}Cov\left({C}_{ij}^N,{C}_{kl}^N\right)&={N}^{-2}\; NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\\&\quad-{N}^{-3}\left(N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)+N\left(N-1\right) Cov\left({X}_i{X}_j,{X}_k\right)\mathbb{E}\left({X}_l\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\right)\\&\quad-{N}^{-3}\left(N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_j\right)\mathbb{E}\left({X}_i\right)+N\left(N-1\right) Cov\left({X}_k{X}_l,{X}_i\right)\mathbb{E}\left({X}_j\right)+ NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\right)+\end{align*}$$
 $$\begin{align*}{N}^{-4}\left(\begin{array}{c}N\left(N-1\right)\left(N-2\right)\left(\begin{array}{c} Cov\left({X}_j,{X}_l\right)\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_k\right)+ Cov\left({X}_i,{X}_l\right)\mathbb{E}\left({X}_j\right)\mathbb{E}\left({X}_k\right)+\\ {} Cov\left({X}_j,{X}_k\right)\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_l\right)+ Cov\left({X}_i,{X}_k\right)\mathbb{E}\left({X}_j\right)\mathbb{E}\left({X}_l\right)\end{array}\right)\\ {}+N\left(N-1\right)\left(\begin{array}{c} Cov\left({X}_k{X}_l,{X}_j\right)\mathbb{E}\left({X}_i\right)+ Cov\left({X}_k{X}_l,{X}_i\right)\mathbb{E}\left({X}_j\right)+\\ {} Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)+ Cov\left({X}_i{X}_j,{X}_k\right)\mathbb{E}\left({X}_l\right)\end{array}\right)+\\ {}N\left(N-1\right)\left(\mathbb{E}\left({X}_i{X}_l\right)\mathbb{E}\left({X}_j{X}_k\right)+\mathbb{E}\left({X}_j{X}_l\right)\mathbb{E}\left({X}_i{X}_k\right)-2\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_j\right)\mathbb{E}\left({X}_k\right)\mathbb{E}\left({X}_l\right)\right)+\\ {} NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\end{array}\right)\end{align*}$$
$$\begin{align*}{N}^{-4}\left(\begin{array}{c}N\left(N-1\right)\left(N-2\right)\left(\begin{array}{c} Cov\left({X}_j,{X}_l\right)\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_k\right)+ Cov\left({X}_i,{X}_l\right)\mathbb{E}\left({X}_j\right)\mathbb{E}\left({X}_k\right)+\\ {} Cov\left({X}_j,{X}_k\right)\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_l\right)+ Cov\left({X}_i,{X}_k\right)\mathbb{E}\left({X}_j\right)\mathbb{E}\left({X}_l\right)\end{array}\right)\\ {}+N\left(N-1\right)\left(\begin{array}{c} Cov\left({X}_k{X}_l,{X}_j\right)\mathbb{E}\left({X}_i\right)+ Cov\left({X}_k{X}_l,{X}_i\right)\mathbb{E}\left({X}_j\right)+\\ {} Cov\left({X}_i{X}_j,{X}_l\right)\mathbb{E}\left({X}_k\right)+ Cov\left({X}_i{X}_j,{X}_k\right)\mathbb{E}\left({X}_l\right)\end{array}\right)+\\ {}N\left(N-1\right)\left(\mathbb{E}\left({X}_i{X}_l\right)\mathbb{E}\left({X}_j{X}_k\right)+\mathbb{E}\left({X}_j{X}_l\right)\mathbb{E}\left({X}_i{X}_k\right)-2\mathbb{E}\left({X}_i\right)\mathbb{E}\left({X}_j\right)\mathbb{E}\left({X}_k\right)\mathbb{E}\left({X}_l\right)\right)+\\ {} NCov\left({X}_i{X}_j,{X}_k{X}_l\right)\end{array}\right)\end{align*}$$
A2 The covariance of two sums of conditional covariances with fixed weights
In the test proposed by Rosenbaum’s (Reference Rosenbaum1984) case 2, the covariance of two items is considered conditionally on the sum of the other items. The statistics used by Rosenbaum is a standardization of a weighted sum of covariances, where the subgroup sizes act as weights. We will now develop a formula for the covariance of a weighted sum of conditional covariances. Let
![]() ${R}_{ij}$
be the variable that is used for the conditioning of pair
${R}_{ij}$
be the variable that is used for the conditioning of pair
![]() $\left({X}_i,{X}_j\right)$
. In the case of Rosenbaum’s case 2,
$\left({X}_i,{X}_j\right)$
. In the case of Rosenbaum’s case 2,
![]() ${R}_{ij}$
would be the sum of the other items, but for our purposes it is sufficient to assume that the range of
${R}_{ij}$
would be the sum of the other items, but for our purposes it is sufficient to assume that the range of
![]() ${R}_{ij}$
is some finite set. The null hypothesis would now be that
${R}_{ij}$
is some finite set. The null hypothesis would now be that
![]() $Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)\ge 0$
for each
$Cov\left({X}_i,{X}_j|{R}_{ij}=s\right)\ge 0$
for each
![]() $s$
in the range of
$s$
in the range of
![]() ${R}_{ij}$
. Denote the corresponding sample covariance as
${R}_{ij}$
. Denote the corresponding sample covariance as
Let
![]() ${N}_{ijs}$
be the number of subjects in the subsample with
${N}_{ijs}$
be the number of subjects in the subsample with
![]() ${R}_{ij}=s$
. Rosenbaum’s statistics is based on standardization of
${R}_{ij}=s$
. Rosenbaum’s statistics is based on standardization of
The goal of this section is to obtain a formula for
![]() $Cov\left({C}_{ij+},{C}_{kl+}\right)$
. As a first step,
$Cov\left({C}_{ij+},{C}_{kl+}\right)$
. As a first step,
We will now first develop
![]() $Cov({C}_{ijs},{C}_{klt})$
. In this section, we will assume that
$Cov({C}_{ijs},{C}_{klt})$
. In this section, we will assume that
![]() ${N}_{ijs}$
and
${N}_{ijs}$
and
![]() ${N}_{klt}$
are fixed numbers instead of random variables. Then
${N}_{klt}$
are fixed numbers instead of random variables. Then
![]() $\sum _s\sum _t Cov({N}_{ijs}{C}_{ijs},{N}_{klt}{C}_{klt})=\sum _s\sum _t{N}_{ijs}{N}_{klt} Cov({C}_{ijs},{C}_{klt})$
, so a formula for
$\sum _s\sum _t Cov({N}_{ijs}{C}_{ijs},{N}_{klt}{C}_{klt})=\sum _s\sum _t{N}_{ijs}{N}_{klt} Cov({C}_{ijs},{C}_{klt})$
, so a formula for
![]() $Cov\left({C}_{ijs},{C}_{klt}\right)$
would solve the problem. In Rosenbaum’s (Reference Rosenbaum1984) application, the
$Cov\left({C}_{ijs},{C}_{klt}\right)$
would solve the problem. In Rosenbaum’s (Reference Rosenbaum1984) application, the
![]() ${N}_{ijs}$
and
${N}_{ijs}$
and
![]() ${N}_{klt}$
are actually random variables, as discussed in the main text.
${N}_{klt}$
are actually random variables, as discussed in the main text.
Let
![]() ${I}_{ij s}^{(n)}=1\left[{R}_{ij}^{(n)}=s\right]$
, the indicator function for the event
${I}_{ij s}^{(n)}=1\left[{R}_{ij}^{(n)}=s\right]$
, the indicator function for the event
![]() ${R}_{ij}=s$
in subject
${R}_{ij}=s$
in subject
![]() $n$
. That is,
$n$
. That is,
![]() $1\left[{R}_{ij}^{(n)}=s\right]=1$
if
$1\left[{R}_{ij}^{(n)}=s\right]=1$
if
![]() ${R}_{ij}^{(n)}=s$
, and
${R}_{ij}^{(n)}=s$
, and
![]() $1\left[{R}_{ij}^{(n)}=s\right]=0$
otherwise, so that
$1\left[{R}_{ij}^{(n)}=s\right]=0$
otherwise, so that
![]() ${N}_{ijs}=\sum _{n=1}^N{I}_{ijs}^{(n)}$
. Then
${N}_{ijs}=\sum _{n=1}^N{I}_{ijs}^{(n)}$
. Then
 $$\begin{align*}{C}_{ijs}=\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\end{align*}$$
$$\begin{align*}{C}_{ijs}=\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}-\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\end{align*}$$
 $$\begin{align*}{C}_{klt}=\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)}}{N_{klt}}-\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{I}_{klt}^{(n)}}{N_{klt}}\frac{\sum \limits_{n=1}^N{X}_l^{(n)}{I}_{klt}^{(n)}}{N_{klt}}\end{align*}$$
$$\begin{align*}{C}_{klt}=\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)}}{N_{klt}}-\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{I}_{klt}^{(n)}}{N_{klt}}\frac{\sum \limits_{n=1}^N{X}_l^{(n)}{I}_{klt}^{(n)}}{N_{klt}}\end{align*}$$
Therefore
![]() $Cov\left({C}_{ijs},{C}_{klt}\right)$
can be developed analogously to the one-sample case of the previous section. We start with rewriting it into four main terms.
$Cov\left({C}_{ijs},{C}_{klt}\right)$
can be developed analogously to the one-sample case of the previous section. We start with rewriting it into four main terms.
 $$\begin{align*}Cov\left({C}_{ijs},{C}_{klt}\right)&= Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\right)\\&\quad- Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\frac{\sum \limits_{r=1}^N{X}_l^{(r)}{I}_{klt}^{(r)}}{N_{klt}}\right)\\&\quad- Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)}}{N_{klt}}\right)\\&\quad+ Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\frac{\sum \limits_{r=1}^N{X}_l^{(r)}{I}_{klt}^{(r)}}{N_{klt}}\right)\end{align*}$$
$$\begin{align*}Cov\left({C}_{ijs},{C}_{klt}\right)&= Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\right)\\&\quad- Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\frac{\sum \limits_{r=1}^N{X}_l^{(r)}{I}_{klt}^{(r)}}{N_{klt}}\right)\\&\quad- Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{n=1}^N{X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)}}{N_{klt}}\right)\\&\quad+ Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}}\frac{\sum \limits_{n=1}^N{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\frac{\sum \limits_{r=1}^N{X}_l^{(r)}{I}_{klt}^{(r)}}{N_{klt}}\right)\end{align*}$$
 $$\begin{align*}&=\frac{1}{N_{ijs}{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}\right)\\&\quad-\frac{1}{N_{ijs}{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{I}_{klt}^{(m)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)\\&\quad-\frac{1}{N_{ijs}^2{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)},{X}_i^{(m)}{I}_{ijs}^{(m)}{X}_j^{(r)}{I}_{ijs}^{(r)}\right)\\&\quad+\frac{1}{N_{ijs}^2{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{q=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{I}_{ijs}^{(n)}{X}_j^{(m)}{I}_{ijs}^{(m)},{X}_k^{(q)}{I}_{klt}^{(q)}{X}_l^{(r)}{I}_{klt}^{(r)}\right).\end{align*}$$
$$\begin{align*}&=\frac{1}{N_{ijs}{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}\right)\\&\quad-\frac{1}{N_{ijs}{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{I}_{klt}^{(m)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)\\&\quad-\frac{1}{N_{ijs}^2{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)},{X}_i^{(m)}{I}_{ijs}^{(m)}{X}_j^{(r)}{I}_{ijs}^{(r)}\right)\\&\quad+\frac{1}{N_{ijs}^2{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{q=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{I}_{ijs}^{(n)}{X}_j^{(m)}{I}_{ijs}^{(m)},{X}_k^{(q)}{I}_{klt}^{(q)}{X}_l^{(r)}{I}_{klt}^{(r)}\right).\end{align*}$$
Using the results of the previous section, we can express these terms as covariance of the variables
![]() ${X}_i{I}_{ijs}$
,
${X}_i{I}_{ijs}$
,
![]() ${X}_j{I}_{ijs}$
,
${X}_j{I}_{ijs}$
,
![]() ${X}_k{I}_{klt}$
, and
${X}_k{I}_{klt}$
, and
![]() ${X}_l{I}_{klt}$
and their products. The first main term is
${X}_l{I}_{klt}$
and their products. The first main term is
 $$\begin{align*}Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\right)&=\frac{1}{N_{ijs}{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}\right)\\&=\frac{N}{N_{ijs}{N}_{klt}} Cov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right).\end{align*}$$
$$\begin{align*}Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\right)&=\frac{1}{N_{ijs}{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{X}_l^{(m)}{I}_{klt}^{(m)}\right)\\&=\frac{N}{N_{ijs}{N}_{klt}} Cov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right).\end{align*}$$
The second main term is
 $$\begin{align*}- Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\frac{\sum \limits_{r=1}^N{X}_l^{(r)}{I}_{klt}^{(r)}}{N_{klt}}\right)&=-\frac{1}{N_{ijs}{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{I}_{klt}^{(m)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)\\&=-\frac{1}{N_{ijs}{N}_{klt}^2}(N\left(N-1\right) Cov\left({X}_i{X}_j{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\&\quad+N\left(N-1\right) Cov\left({X}_i{X}_j{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\\&\quad+ NCov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right)).\end{align*}$$
$$\begin{align*}- Cov\left(\frac{\sum \limits_{n=1}^N{X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)}}{N_{ijs}},\frac{\sum \limits_{m=1}^N{X}_k^{(m)}{I}_{klt}^{(m)}}{N_{klt}}\frac{\sum \limits_{r=1}^N{X}_l^{(r)}{I}_{klt}^{(r)}}{N_{klt}}\right)&=-\frac{1}{N_{ijs}{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{I}_{klt}^{(m)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)\\&=-\frac{1}{N_{ijs}{N}_{klt}^2}(N\left(N-1\right) Cov\left({X}_i{X}_j{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\&\quad+N\left(N-1\right) Cov\left({X}_i{X}_j{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\\&\quad+ NCov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right)).\end{align*}$$
This is developed in Table A3.
Table A3
Development of the term
![]() $\sum _{n=1}^N\sum _{m=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{I}_{klt}^{(m)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)$
$\sum _{n=1}^N\sum _{m=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{X}_j^{(n)}{I}_{ijs}^{(n)},{X}_k^{(m)}{I}_{klt}^{(m)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)$

The third main term is analogously,
 $$\begin{align*}&\quad-\frac{1}{N_{ijs}^2{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)},{X}_i^{(m)}{I}_{ijs}^{(m)}{X}_j^{(r)}{I}_{ijs}^{(r)}\right)\\&=-\frac{1}{N_{ijs}^2{N}_{klt}}(N\left(N-1\right) Cov\left({X}_k{X}_l{I}_{klt},{X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\\&\quad+N\left(N-1\right) Cov\left({X}_k{X}_l{I}_{klt},{X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)+ NCov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right)).\end{align*}$$
$$\begin{align*}&\quad-\frac{1}{N_{ijs}^2{N}_{klt}}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{r=1}^N Cov\left({X}_k^{(n)}{X}_l^{(n)}{I}_{klt}^{(n)},{X}_i^{(m)}{I}_{ijs}^{(m)}{X}_j^{(r)}{I}_{ijs}^{(r)}\right)\\&=-\frac{1}{N_{ijs}^2{N}_{klt}}(N\left(N-1\right) Cov\left({X}_k{X}_l{I}_{klt},{X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\\&\quad+N\left(N-1\right) Cov\left({X}_k{X}_l{I}_{klt},{X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)+ NCov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right)).\end{align*}$$
The fourth main term is
 $$\begin{align*}&\frac{1}{N_{ijs}^2{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{q=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{I}_{ijs}^{(n)}{X}_j^{(m)}{I}_{ijs}^{(m)},{X}_k^{(q)}{I}_{klt}^{(q)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)\\&=\frac{1}{N_{ijs}^2{N}_{klt}^2}\left(\begin{array}{c}N\left(N-1\right)\left(N-2\right)\left(\begin{array}{c} Cov\left({X}_j{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\ {}+ Cov\left({X}_i{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\ {}+ Cov\left({X}_j{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\\ {}+ Cov\left({X}_i{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\end{array}\right)\\ {}+\\ {}N\left(N-1\right)\left(\begin{array}{c} Cov\left({X}_k{X}_l{I}_{klt},{X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\\ {}+ Cov\left({X}_k{X}_l{I}_{klt},{X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\\ {}+ Cov\left({X}_i{X}_j{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\ {}+ Cov\left({X}_i{X}_j{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\end{array}\right)\\ {}+\\ {}N\left(N-1\right)\left(\begin{array}{c}\mathbb{E}\left({X}_i{I}_{ijs}{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_j{I}_{ijs}{X}_k{I}_{klt}\right)+\mathbb{E}\left({X}_j{I}_{ijs}{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_i{I}_{ijs}{X}_k{I}_{klt}\right)\\ {}-2\mathbb{E}\left({X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\end{array}\right)\\ {}+\\ {} NCov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right)\end{array}\right)\end{align*}$$
$$\begin{align*}&\frac{1}{N_{ijs}^2{N}_{klt}^2}\sum \limits_{n=1}^N\sum \limits_{m=1}^N\sum \limits_{q=1}^N\sum \limits_{r=1}^N Cov\left({X}_i^{(n)}{I}_{ijs}^{(n)}{X}_j^{(m)}{I}_{ijs}^{(m)},{X}_k^{(q)}{I}_{klt}^{(q)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)\\&=\frac{1}{N_{ijs}^2{N}_{klt}^2}\left(\begin{array}{c}N\left(N-1\right)\left(N-2\right)\left(\begin{array}{c} Cov\left({X}_j{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\ {}+ Cov\left({X}_i{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\ {}+ Cov\left({X}_j{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\\ {}+ Cov\left({X}_i{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\end{array}\right)\\ {}+\\ {}N\left(N-1\right)\left(\begin{array}{c} Cov\left({X}_k{X}_l{I}_{klt},{X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_i{I}_{ijs}\right)\\ {}+ Cov\left({X}_k{X}_l{I}_{klt},{X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\\ {}+ Cov\left({X}_i{X}_j{I}_{ijs},{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\\ {}+ Cov\left({X}_i{X}_j{I}_{ijs},{X}_k{I}_{klt}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\end{array}\right)\\ {}+\\ {}N\left(N-1\right)\left(\begin{array}{c}\mathbb{E}\left({X}_i{I}_{ijs}{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_j{I}_{ijs}{X}_k{I}_{klt}\right)+\mathbb{E}\left({X}_j{I}_{ijs}{X}_l{I}_{klt}\right)\mathbb{E}\left({X}_i{I}_{ijs}{X}_k{I}_{klt}\right)\\ {}-2\mathbb{E}\left({X}_i{I}_{ijs}\right)\mathbb{E}\left({X}_j{I}_{ijs}\right)\mathbb{E}\left({X}_k{I}_{klt}\right)\mathbb{E}\left({X}_l{I}_{klt}\right)\end{array}\right)\\ {}+\\ {} NCov\left({X}_i{X}_j{I}_{ijs},{X}_k{X}_l{I}_{klt}\right)\end{array}\right)\end{align*}$$
This is developed in Table A4.
Table A4
Development of
![]() $\sum _{n=1}^N\sum _{m=1}^N\sum _{q=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{I}_{ijs}^{(n)}{X}_j^{(m)}{I}_{ijs}^{(m)},{X}_k^{(q)}{I}_{klt}^{(q)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)$
$\sum _{n=1}^N\sum _{m=1}^N\sum _{q=1}^N\sum _{r=1}^N Cov\left({X}_i^{(n)}{I}_{ijs}^{(n)}{X}_j^{(m)}{I}_{ijs}^{(m)},{X}_k^{(q)}{I}_{klt}^{(q)}{X}_l^{(r)}{I}_{klt}^{(r)}\right)$

Let us now summarize the results. For arbitrary variables
![]() $V,W,X,Y$
write
$V,W,X,Y$
write
 $$\begin{align*}{\gamma}_5\left(V,W,X,Y\right)&= Cov\left( VW,X\right)\mathbb{E}(Y)+ Cov\left( VW,Y\right)\mathbb{E}(X)+ Cov\left(V, XY\right)\mathbb{E}(W)+ Cov\left(W, XY\right)\mathbb{E}(V)\\&={\gamma}_2\left(V,W,X,Y\right)+{\gamma}_3\left(V,W,X,Y\right)\end{align*}$$
$$\begin{align*}{\gamma}_5\left(V,W,X,Y\right)&= Cov\left( VW,X\right)\mathbb{E}(Y)+ Cov\left( VW,Y\right)\mathbb{E}(X)+ Cov\left(V, XY\right)\mathbb{E}(W)+ Cov\left(W, XY\right)\mathbb{E}(V)\\&={\gamma}_2\left(V,W,X,Y\right)+{\gamma}_3\left(V,W,X,Y\right)\end{align*}$$
and
 $$\begin{align*}{T}_4\left(V,W,X,Y,N\right)&=N\left(N-1\right)\left(N-2\right){\gamma}_4\left(V,W,X,Y\right)\\&\quad+N\left(N-1\right){\gamma}_5\left(V,W,X,Y\right)+N\left(N-1\right){\gamma}_6\left(V,W,X,Y\right)+N{\gamma}_1\left(V,W,X,Y\right).\end{align*}$$
$$\begin{align*}{T}_4\left(V,W,X,Y,N\right)&=N\left(N-1\right)\left(N-2\right){\gamma}_4\left(V,W,X,Y\right)\\&\quad+N\left(N-1\right){\gamma}_5\left(V,W,X,Y\right)+N\left(N-1\right){\gamma}_6\left(V,W,X,Y\right)+N{\gamma}_1\left(V,W,X,Y\right).\end{align*}$$
Then the result of the previous section can be written as
The result of the present section can be obtained with
![]() $V={X}_i{I}_{ijs}$
,
$V={X}_i{I}_{ijs}$
,
![]() $W={X}_j{I}_{ijs}$
,
$W={X}_j{I}_{ijs}$
,
![]() $X={X}_k{I}_{klt}$
,
$X={X}_k{I}_{klt}$
,
![]() $Y={X}_l{I}_{klt}$
:
$Y={X}_l{I}_{klt}$
:
 $$\begin{align*}Cov\left({C}_{ijs},{C}_{klt}\right)&=\frac{1}{N_{ijs}{N}_{klt}}{T}_1\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{ijs}{N}_{klt}^2}{T}_2\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{ijs}^2{N}_{klt}}{T}_3\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad+\frac{1}{N_{ijs}^2{N}_{klt}^2}{T}_4\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right).\end{align*}$$
$$\begin{align*}Cov\left({C}_{ijs},{C}_{klt}\right)&=\frac{1}{N_{ijs}{N}_{klt}}{T}_1\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{ijs}{N}_{klt}^2}{T}_2\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{ijs}^2{N}_{klt}}{T}_3\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad+\frac{1}{N_{ijs}^2{N}_{klt}^2}{T}_4\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right).\end{align*}$$
Thus
 $$\begin{align*}Cov\left({N}_{ijs}{C}_{ijs},{N}_{klt}{C}_{klt}\right)&={T}_1\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{klt}}{T}_2\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{ijs}}{T}_3\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad+\frac{1}{N_{ijs}{N}_{klt}}{T}_4\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right).\end{align*}$$
$$\begin{align*}Cov\left({N}_{ijs}{C}_{ijs},{N}_{klt}{C}_{klt}\right)&={T}_1\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{klt}}{T}_2\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad-\frac{1}{N_{ijs}}{T}_3\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right)\\&\quad+\frac{1}{N_{ijs}{N}_{klt}}{T}_4\left({X}_i{I}_{ijs},{X}_j{I}_{ijs},{X}_k{I}_{klt},{X}_l{I}_{klt},N\right).\end{align*}$$