Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-07T19:00:39.071Z Has data issue: false hasContentIssue false
  • English
  • Français

The Impact of Fallible Item Parameter Estimates on Latent Trait Recovery

Published online by Cambridge University Press:  01 January 2025

Ying Cheng  and
Ke-Hai Yuan
Ying Cheng*
Affiliation:
University of Notre Dame
Ke-Hai Yuan
Affiliation:
University of Notre Dame
*
Requests for reprints should be sent to Ying Cheng, University of Notre Dame, 118 Haggar Hall, Notre Dame, IN 46556, USA. E-mail: ycheng4@nd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we propose an upward correction to the standard error (SE) estimation of \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\hat{\theta}_{\mathrm{ML}}$\end{document}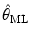, the maximum likelihood (ML) estimate of the latent trait in item response theory (IRT). More specifically, the upward correction is provided for the SE of \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\hat{\theta}_{\mathrm{ML}}$\end{document} 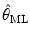when item parameter estimates obtained from an independent pretest sample are used in IRT scoring. When item parameter estimates are employed, the resulting latent trait estimate is called pseudo maximum likelihood (PML) estimate. Traditionally, the SE of \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$\hat{\theta}_{\mathrm{ML}}$\end{document} 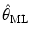is obtained on the basis of test information only, as if the item parameters are known. The upward correction takes into account the error that is carried over from the estimation of item parameters, in addition to the error in latent trait recovery itself. Our simulation study shows that both types of SE estimates are very good when θ is in the middle range of the latent trait distribution, but the upward-corrected SEs are more accurate than the traditional ones when θ takes more extreme values.

Keywords

IRT scoringpseudo maximum likelihood (PML)standard errorupward correctionlatent trait estimation
Type
Theory and Methods
Information
Psychometrika , Volume 75 , Issue 2 , June 2010 , pp. 280 - 291
Copyright
Copyright © 2010 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Both authors made equal contributions to the paper, and the order of authorship is alphabetical. The authors would like to thank the Associate Editor and two anonymous reviewers for their insightful suggestions and comments. Ke-Hai Yuan’s research on this project was supported by grant 4R44CA137841 from the National Cancer Institute.

References

Baker, F.B., & Kim, S.H. (2004). Item response theory: Parameter estimation techniques, (2nd ed.). New York: Dekker.CrossRefGoogle Scholar
Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In Lord, F.M., & Novick, M.R. (Eds.), Statistical theories of mental test scores (pp. 397–472). Reading: Addison-Wesley.Google Scholar
Bock, R.D., & Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 46, 443–459.CrossRefGoogle Scholar
Cai, L. (2008). SEM of another flavour: Two new applications of the supplemented EM algorithm. British Journal of Mathematical and Statistical Psychology, 61, 309–329.CrossRefGoogle ScholarPubMed
Cover, T.M., & Thomas, J.A. (1991). Elements of information theory, New York: Wiley.Google Scholar
Embretson, S.E., & Reise, S.P. (2000). Item response theory for psychologists, Mahwah: Erlbaum.Google Scholar
Godambe, V.P., & Thompson, M.E. (1974). Estimating equations in the presence of a nuisance parameter. The Annals of Statistics, 2, 568–571.CrossRefGoogle Scholar
Gong, G., & Samaniego, F. (1981). Pseudo-maximum likelihood estimation: Theory and applications. The Annals of Statistics, 9, 861–869.CrossRefGoogle Scholar
Hambleton, R., & Swaminathan, H. (1985). Item response theory: Principles and applications, Boston: Kluwer-Nijhoff Publishing.CrossRefGoogle Scholar
Harwell, M.R., & Baker, F.B. (1991). The use of prior distributions in marginalized Bayesian item parameter estimation: A didactic. Applied Psychological Measurement, 15, 375–389.CrossRefGoogle Scholar
Harwell, M.R., Baker, F.B., & Zwarts, M. (1988). Item parameter estimation via marginal maximum likelihood and an EM algorithm: A didactic. Journal of Educational Statistics, 13, 243–271.CrossRefGoogle Scholar
Parke, W.R. (1986). Pseudo maximum likelihood estimation: The asymptotic distribution. The Annals of Statistics, 14, 355–357.CrossRefGoogle Scholar
Patz, R.J., & Junker, B.W. (1999). A straightforward approach to Markov chain Monte Carlo methods for item response models. Journal of Educational and Behavioral Statistics, 24, 146–178.CrossRefGoogle Scholar
Tsutakawa, R.K., & Johnson, J.C. (1990). The effect of uncertainty of item parameter estimation on ability estimates. Psychometrika, 55, 371–390.CrossRefGoogle Scholar
Yuan, K.-H., & Jennrich, R.I. (2000). Estimating equations with nuisance parameters: Theory and applications. Annals of the Institute of Statistical Mathematics, 52, 343–350.CrossRefGoogle Scholar
Wingersky, M.S., Barton, M.A., & Lord, F.M. (1982). LOGIST user’s guide, Princeton: Educational Testing Service.Google Scholar
Zimowski, M., Muraki, E., Mislevy, R.J., & Bock, R.D. (2003). BILOG-MG 3: Item analysis and test scoring with binary logistic models. Chicago: Scientific Software [Computer software].Google Scholar