People make hundreds of decisions each day. For instance, car drivers search for traffic signs and decide to slow down or yield right-of-way (Ho, Scialfa, Caird, & Graw, Reference Ho, Scialfa, Caird and Graw2001), airport security personnel search for weapons in X-ray images of luggage and decide whether to do a physical examination (McCarley, Kramer, Wickens, Vidoni, & Boot, Reference McCarley, Kramer, Wickens, Vidoni and Boot2004), radiologists search for nodules on mammograms and chest radiographs and decide which ones are potentially cancerous (Krupinski, Berger, Dallas, & Roehrig, Reference Krupinski, Berger, Dallas and Roehrig2003; Wedel, Yan, Siegel, & Li, Reference Wedel, Yan, Siegel and Li2016), people look at facial characteristics to decide which person they like (Chuk, Chan, Shimojo, & Hsiao, Reference Chuk, Chan, Shimojo and Hsiao2020), consumers search for products on websites and shelves (Shi, Wedel, & Pieters, Reference Shi, Wedel and Pieters2013; van der Lans, Pieters, & Wedel, Reference van der Lans, Pieters and Wedel2008b), search for information about prices, ingredients, and sustainability on packages (van Herpen & van Trijp, Reference van Herpen and van Trijp2011), and choose the products they expect to satisfy their needs (Stüttgen, Boatwright, & Monroe, Reference Stüttgen, Boatwright and Monroe2012). All these decisions involve search as well as choice. The underlying cognitive mechanisms rely heavily on acquisition and processing of visual information.
There is a long history of research into search and choice behaviors in psychology and related disciplines (examples are Berlyne, Reference Berlyne1971; Russo & Rosen, Reference Russo and Rosen1975; Wolfe, Reference Wolfe1998; Yarbus, Reference Yarbus1967). This research has yielded a deep understanding of the underlying fundamental processes. Yet, three challenges face this literature. First, although many forms of decision making involve visual search, search and choice have been addressed in disparate streams of research, which has resulted in suboptimal cross-fertilization of knowledge. Second, much of the research in question has relied on endpoint measures, such as response times and the final choices made, to infer the underlying cognitive mechanisms of interest (Luce, Reference Luce1977; McFadden, Reference McFadden1974; Treisman & Gelade, Reference Treisman and Gelade1980; Wolfe, Reference Wolfe1998). Such endpoint measures have proven to be valuable, but do not always provide unambiguous evidence for the underlying processes (Sanders & Donk, Reference Sanders and Donk1996; Zelinsky, Reference Zelinsky2008). Third, extant research has often relied on simple stimuli and controlled tasks in high-repetition, within-participant designs to uniquely identify the processes of interest. These controlled experiments ensure a high internal validity of hypothesis tests, yet may suffer from limited ecological validity of inferences on the cognitive processes as they play out in real-life contexts.
There is growing interest in understanding search and choice in the common, more complex, messy, and less controlled tasks that people encounter in their daily lives. Such research faces critical challenges because search and choice behaviors are often involved in the same task, and multiple unobserved cognitive processes may simultaneously cause variations in the associated endpoint measures. Eye movements are unique process measures to study search and choice behavior in such natural contexts (Findlay & Gilchrist, Reference Findlay and Gilchrist2003; Najemnik & Geisler, Reference Najemnik and Geisler2005; Zelinsky, Reference Zelinsky2008). Eye movements reflect, with a high temporal and spatial resolution, several unobserved perceptual, cognitive and evaluative processes (Findlay & Gilchrist, Reference Findlay and Gilchrist1998). They enable a fine-grained process analysis with the potential of yielding insights that are difficult to obtain otherwise, especially in real-life contexts. For example, eye movements have provided insights into information search during advertising exposure (Wedel & Pieters, Reference Wedel and Pieters2000) and brand choice (Shi et al., Reference Shi, Wedel and Pieters2013), the determinant processes of which are largely inaccessible to self-reports (Aribarg, Pieters, & Wedel, Reference Aribarg, Pieters and Wedel2010; Nisbett & Wilson, Reference Nisbett and Wilson1977) or to alternative process-tracing techniques such as information display boards (Lohse & Johnson, Reference Lohse and Johnson1996). Statistical models have proven to be indispensable for making inferences on these unobservable processes, in psychology, economics and marketing, because they enable disentangling the effects of multiple unobserved processes from the eye-movement recordings (Stüttgen et al., Reference Stüttgen, Boatwright and Monroe2012; van der Lans et al., Reference van der Lans, Pieters and Wedel2008b; Yang, Toubia, & de Jong, Reference Yang, Toubia and de Jong2015). Understanding the mechanisms that drive search and choice may lead to better predictions and has ramifications for policy makers, companies, and consumers, for example by enabling better design and testing of policy and medical interventions, websites, store shelves, advertisements, and labels on food packaging (e.g., Van Loo, Grebitus, Nayga Jr., Verbeke, & Roosen, Reference Van Loo, Grebitus, Nayga, Verbeke and Roosen2018).
Several streams of research have examined search and choice behaviors in natural environments by using eye-movement measures and statistical, psychometric, or econometric models. Earlier reviews have summarized advances in eye-tracking research, in general (Rayner, Reference Rayner1998; Wedel & Pieters, Reference Wedel and Pieters2008a) and for search and choice separately (Glaholt & Reingold, Reference Glaholt and Reingold2011; Kowler, Reference Kowler2011; Orquin & Loose, Reference Orquin and Loose2013), or have conducted meta-analyses of eye movements during choice (Orquin, Lahm, & Stojić, Reference Orquin, Lahm and Stojić2021). The present article reviews the advances made in the modeling of eye movements during decision making. We aim to make a step toward an integrated account of the cognitive processes fundamental to decision making by highlighting the role of task and strategy switching during such decision making. We provide a theoretical framework that summarizes the key tasks involved and the processes underlying eye movements during decision making. We place the extant literature within that framework, highlight recent advances in modeling eye-movement behaviors, discuss limitations, challenges, and open problems, and provide an agenda for future research. We believe that such a review of the literature is timely, because the cost of eye-tracking equipment has come down enormously and relatively unobtrusive eye-movement recording is now possible in a wide variety of real-life contexts, while the psychometric toolbox to extract information from eye-tracking data is rapidly growing. Even so, eye-movement recording and modeling during search and choice is still underutilized both in academic and in applied research, a situation which we hope this review will help to improve.
Section 1 briefly introduces eye movements and eye-movement recording. Section 2 presents our framework of tasks, task switching, and attentional processes underlying eye movements during decision making. Section 3 summarizes models for each of those processes during search. Section 4 reviews, against this backdrop, the literature on eye-movement analysis during choice. Section 5 provides an outlook for novel applications and future developments.
1. Eye Movements and Their Recording
1.1. Eye Movements and Visual Attention
We use the term (visual) attention as a container for various cognitive processes that are involved in the selection of relevant and the suppression of irrelevant information during search and choice, for which according to James (Reference James1890, pp. 403–404): “Focalization, concentration, and consciousness are of […] essence.” The next section describes these processes and their links to eye movements. It is important to point out that in most natural decision-making tasks, eye-movement patterns are valid and accurate indicators of the hidden attention processes of interest (Findlay, Reference Findlay2005). There are also successful examples of inferences on higher order cognitive states from eye movements, such as on tasks and goals (Borji & Itti, Reference Borji and Itti2014; Haji-Abolhassani & Clark, Reference Haji-Abolhassani and Clark2014; Kardan, Berman, Yourganov, Schmidt, & Henderson, Reference Kardan, Berman, Yourganov, Schmidt and Henderson2015) and on the emotional valence of images (Nummenmaa, Hyönä, & Calvo, Reference Nummenmaa, Hyönä and Calvo2006; R.-Tavakoli et al., Reference R.-Tavakoli, Atyabi, Rantanen, Laukka, Nefti-Meziani and Heikkilä2015), although these tend to require additional experimental control, measures, and theoretical assumptions.
At any point in time, the human eye-vision system processes only about one percent of the field of vision with high acuity (Rayner, Reference Rayner1998; Wedel & Pieters, Reference Wedel and Pieters2008a). This is due to the density of photosensitive cells in the human retina decreasing rapidly from a high concentration in a small region in its center (fovea) toward the parafovea and periphery. Therefore, people need to move their eyes to explore their environment in sufficient detail. In practice, people make on average three to six larger eye movements per second during tasks such as reading, scene perception, or decision making (Rayner, Reference Rayner1998). These saccades are fast jumps of the eye’s point of regard (POR) between spatial locations in the environment. Saccades typically last for about 20–40 ms. Fixations are periods of about 100–400 ms when the eyes hardly move. While during a saccade visual perception is suppressed to prevent blurring, during an eye fixation detailed visual information is obtained from a small region of about two degrees of visual angle around the POR.
A scan-path is the spatiotemporal sequence of eye fixations and saccades for a particular task, stimulus, and person. Figure 1 summarizes the scan-paths of four participants who were engaged in a target search task: they searched on a shopping website for a brand of perfume to choose as a gift. The figure (based on data from study 2 in van der Lans, Pieters, & Wedel, Reference van der Lans, Pieters and Wedel2021) reveals several key features of the scan-paths which inform theories and psychometric models. First, the first fixation commonly lands close to the center of the screen. This location may be optimal because it has the smallest distance to all other locations. Second, some fixations land on visually salient objects, i.e., objects that stand out from their surroundings in terms of luminance, color, or shape. Other parts of individuals’ scan-paths reflect systematic left-right movements. That pattern may be induced by the organization of the image (scene layout). Third, the scan-paths consist of clusters of fixations on objects, interspersed with saccades toward more distant objects. Those clusters reflect refixations which are used to accumulate information to determine the identity or value of objects of interest. Longer saccades reflect search for where new objects are located. Fourth, a cluster of fixations is specifically directed at the final, chosen object. Such a pattern may reflect preference formation or a final verification of the object before implementing a decision, or it might be that looking at an object longer increases one’s preference for it. Fifth, scan-paths show large individual variation and differ markedly among distinct tasks and stimuli. In addition, the scan-paths of participants who had a different search goal (in the top versus the bottom row of the figure) are noticeably different. We return to all those features of scan-paths in the sequel. The scan-paths observed when people make choices among alternative options are similar to those in Fig. 1 but are often considerably more elaborate.
Next to fixations and saccades, other types of eye movements include micro-saccades which are involuntary movements with small amplitude that occur during fixations, smooth pursuits which are fixations on moving objects, vergence movements which occur to maintain the POR on an object that moves toward or away from the viewer, and pupil movements to regulate the amount of incoming light, amongst others. While the analysis of these movements has been useful for specific problems, the present review focuses on fixations and saccades.
1.2. Eye-Movement Recording
The dominant method of recording eye movements in research on search and choice uses an infrared light source directed at one or both eyes, which creates (invisible) reflections on the cornea, the hard outer layer of each eye, called Purkinje reflections (Duchowski, Reference Duchowski2003). After a short calibration task, video cameras record one or more of these reflections, even while participants move their heads. Based on the calibration results, algorithms infer the POR in x-y stimulus coordinates from these reflections. Commonly used eye trackers are built into desktop monitors or into small stand-alone devices that can be attached to laptops and other objects. In addition, mobile eye trackers embedded in glasses allow free body movements while recording the entire field of view as well as the POR within it. Commercial infrared eye trackers typically sample the POR with a sampling frequency of 50 or 60 Hertz and a spatial accuracy of 0.5 degrees of visual angle, or better. Eye trackers with a higher spatiotemporal precision make use of multiple Purkinje reflections and sampling frequencies of 120 Hertz or more, for which the participant’s head sometimes needs to be fixed during recording with a chin or forehead rest. Further, eye movements can be recorded with regular front-facing (web) cameras integrated into digital devices, by using eye landmarks, such as the center and shape of the pupil and the location of eye corners, as input to computer vision algorithms that estimate gaze direction from images of the eyes. Those eye-tracking solutions still have lower accuracy than infrared eye tracking.
1.3. Eye-Movement Data
Eye tracking during decision making results in large amounts of raw data. For example, an eye-tracking study in which participants make 20 decisions, with 10 s available for each decision and a 50 Hertz sampling frequency, results in some ten thousand samples comprised of the x-y coordinates of the POR of each eye per participant. This amounts to one million data points for a study with one hundred participants. A proportion of the data may involve outliers or may be missing due to eye blinks and tracking problems, however. From the raw samples of the POR, algorithms are used to identify fixations and saccades based on their spatial proximity or the velocity of their movement (Salvucci & Goldberg, Reference Salvucci and Goldberg2000). This reduces the dimensionality of the data by a factor 20 or more. For example, the BIT (Binocular Individual Threshold) algorithm (van der Lans, Wedel, & Pieters, Reference van der Lans, Wedel and Pieters2011) automatically determines fixations using individual-specific eye-velocity thresholds for both eyes, automatically removing eye blinks and other recording abnormalities. Due to blinks, saccades and recording errors, missing data points are common in raw samples of the POR. As a rule of thumb, van der Lans and Wedel (Reference van der Lans and Wedel2017) propose that one may consider removing a participant’s data if less than 80 percent of their raw samples are classified as fixations. Once the fixation data have been prepared, various characteristics of the eye-movement patterns can be examined, such as x-y coordinates of fixations over time, scan-paths, or aggregate measures such as fixation counts, gaze or dwell times, and fixation selection indicators, on so-called Regions of Interest (ROIs) (Holmqvist et al., Reference Holmqvist, Nyström, Andersson, Dewhurst, Jarodzka and van de Weijer2011). The spatial aggregation of fixations on those ROIs, for example by calculating gaze times on the individual perfume bottles in Fig. 1, reduces the size of the data further (the gaze time on a ROI is defined as the sum of the durations of all fixations that land on that ROI). Fixation patterns are often graphically explored via heatmaps, which represent the density of fixations using colors, and fixation plots which depict scan-paths as shown in Fig. 1.

Figure 1. Scan-paths of four participants searching for a brand of perfume to choose on a shopping website. The dots indicate fixations, the lines saccades. Red rectangular boxes indicate the first and last fixation. The top, respectively, bottom, panels show scan-paths for two participants searching for the Jimmy Choo, respectively, the Dolce & Gabana, perfumes (based on data from van der Lans et al., Reference van der Lans, Pieters and Wedel2021).
2.2. Theoretical Framework
Via eye movements, people acquire information to reduce various uncertainties during task completion (Hayhoe & Ballard, Reference Hayhoe and Ballard2005; Land, Reference Land2019; Pieters & Wedel, Reference Pieters and Wedel2007). Decision-making tasks vary in the types of uncertainty that they induce, which influences the eye-movement patterns observed during these tasks. We propose a classification of decision-making tasks in Sect. 2.1 and, building on this, a theoretical framework of eye movements during decision making in Sect. 2.2.
2.1. Decision-Making Tasks
In Table 1, we propose a classification that involves six fundamental decision-making tasks that people commonly engage in. These tasks have in common that they require eye movements. They therefore involve exposure durations longer than the duration of a single fixation (100–300 ms). The tasks elicit different types of uncertainties which people try to resolve through visual information acquisition.
Table 1. Six fundamental decision-making tasks, the types of uncertainty they induce, and the dominant cognitive process involved when engaging in the task.

Table 1 makes a main distinction between perceptual decision making and preferential decision making (e.g., Dutilh & Rieskamp, Reference Dutilh and Rieskamp2016; Summerfield & Blangero, Reference Summerfield and Blangero2017). Perceptual decision-making tasks have an objective (external) performance criterion, mostly speed and/or accuracy. Search tasks are perceptual decision-making tasks. Preferential (or value-based) decision-making tasks have one or more subjective (internal) performance criteria, such as perceived costs and benefits, decision justification, or post-choice satisfaction. The completion of these tasks is based on personal preference or utility functions. Choice tasks are preferential decision-making tasks. The dominant processes involved in the tasks in Table 1 are perception, cognition, and evaluation, respectively (Table 1, column IV). Although cognition is sometimes used in a broader sense to encompass perception and evaluation, here perception refers to the process of acquiring new information via the senses, cognition refers to the processes of storing, retrieving, interpreting, and combining new and existing information, and evaluation refers to assessing the personal value of the information (and acting upon it).
We distinguish six basic tasks, each having its own specific type of uncertainty that people need to reduce (Table 1, columns I and II), and each being at least partly observable from eye movements. 1. Localization aims to reduce uncertainty about the spatial location of a known object; 2. Identification aims to reduce uncertainty about the identity of an object vis-à-vis other objects and/or some object template in memory; 3. Specification aims to reduce uncertainty about the presence of specific attributes or features of an object by associating the object with information on these attributes in memory; 4. Inference aims to reduce uncertainty about the consequences of these attributes and their decision outcomes; 5. Valuation aims to reduce uncertainty about the value or meaningfulness of an object’s attributes and features to the person’s goals; 6. Integration aims to reduce uncertainty about the overall utility of an object (choice alternative) to the person relative to other objects. We use the term “integration,” because people need to integrate expected outcomes and their valuation of these outcomes into their overall assessment of the utility of a stimulus (Anderson & Shanteau, Reference Anderson and Shanteau1970). Integration can take place via some (optimal) subjective expected utility mechanism, as traditionally assumed in economics, or via satisficing mechanisms (Simon, Reference Simon1955). The order of uncertainties in the table from top to bottom corresponds to the hierarchical organization of knowledge structures from bottom-up features of objects to top-down values and preferences of people. It reflects the structure of the human motivation system from concrete means (objects and their attributes), which have expected consequences (outcomes), which satisfy certain abstract ends (values) (Kruglanski, Chernikova, Babush, Dugas, & Schumpe, Reference Kruglanski, Chernikova, Babush, Dugas and Schumpe2015), which contribute to utility.
The tasks that people engage in in real-life contexts are commonly combinations of these six basic tasks. For example, localization (task 1) and identification (task 2) are subtasks of a target search task (van der Lans et al., Reference van der Lans, Pieters and Wedel2008b). Localization (task 1) and specification (task 3) are subtasks of an information search task (Moorthy, Ratchford, & Talukdar, Reference Moorthy, Ratchford and Talukdar1997). Identification (task 2) and specification (task 3) are subtasks of a categorization task (Rosch, Reference Rosch1978), in which people differentiate prototypes from exemplars in a category or exemplars in one category from exemplars in another. It is crucial to note that whereas controlled experiments can be used to isolate a single task or uncertainty, the tasks that people perform in natural settings are mostly comprised of several subtasks, each with their specific uncertainty (Droll & Hayhoe, Reference Droll and Hayhoe2007; Hayhoe & Ballard, Reference Hayhoe and Ballard2005; Locke & Latham, Reference Locke and Latham2002).
2. Theoretical Framework
The classification in Table 1 informs our framework, summarized in Fig. 2, of how people use eye movements to reduce uncertainties inherent in perceptual and preferential decision-making tasks. The framework relates eye movements to the underlying processes of interest. It shows from left to right 1) inputs, 2) processes, and 3) decision outputs. These concepts are organized from bottom to top by level of processing, from features, to scene, objects, and the person. Symbols indicate the links between these concepts.
First, the framework distinguishes five observable exogenous inputs: a) person characteristics (i.e., age, prior knowledge), b) task instructions (i.e., search goal, incentives, time constraints), c) object attributes (i.e., description of objects/products on dimensions such as price, brand name and other qualities), d) scene layout (i.e., how the objects are arranged on a row-column shopping website), and e) perceptual features (i.e., detailed visual characteristics, such as colors and edges of objects). Second, the outputs of decision tasks consist of observable micro- (fixation locations, fixation durations) and macro-decision outcomes (search accuracy, choice, and response time), which are represented at the right-hand side of Fig. 2. Third, in between these observable inputs and outputs are unobserved, or latent, processes, depicted in the center of the figure (connected via P1-P5). These latent processes are affected by exogenous inputs (via links I1-I5), and in turn impact both eye movement (via O1-O2) and choice decisions (via O3-O4).
Task and strategy switching take a central role in the framework. Formally, task switching concerns switching between two or more tasks which each have their own unique goals and uncertainties (Kiesel et al., Reference Kiesel, Steinhauser, Wendt, Falkenstein, Jost, Philipp and Koch2010), whereas strategy switching concerns switching between different ways of pursuing the same task or goal (Shi et al., Reference Shi, Wedel and Pieters2013). In this review, we use the terms interchangeably, because in real-life contexts, empirically the distinction between task and strategy switching is often ambiguous. Decision making in real-life contexts typically involves the deployment of attention to resolve multiple uncertainties over time (Table 1). Therefore, people break up complex decision tasks into multiple simpler subtasks, each of which requires a unique strategy that involves the deployment of attention to resolve the associated uncertainty (Stewart, Hermens, & Matthews, Reference Stewart, Hermens and Matthews2016; Stojić, Orquin, Dayan, Dolan, & Speekenbrink, Reference Stojić, Orquin, Dayan, Dolan and Speekenbrink2020). People switch between these subtasks over time to assess the utility of decision alternatives and meet the overall decision goal, under cognitive cost and effort constraints. They monitor goal progress within tasks, and switch when a task nears completion and/or incremental expected utility drops below or cost rises above a threshold (Gutzwiller, Wickens, & Clegg, Reference Gutzwiller, Wickens and Clegg2019). Such task/strategy switching characterizes goal pursuit and decision making in complex, realistic contexts (Locke & Latham, Reference Locke and Latham2002). The next sections describe the attention processes during decision making. Appendix 1 summarizes the neuroscientific basis of attention and eye movements.

Figure 2. Eye movements and decision task performance. Framework for how people use eye movements to reduce uncertainties inherent in perceptual and preferential decision-making tasks. Observable exogenous inputs to the decision processes are on the left side; unobservable perceptual, cognitive, and evaluative processes are in the center; observable decision outcomes are on the right-side. Inputs and processes are organized from top to bottom by level of visual processing: person, object, scene, and feature. Arrows depict the links between inputs and processes (I1 to I5), between unobserved processes (P1 to P5), and between processes and decision outputs (O1 to O4).
2.2.1. Eye Movements and Attention
Overt (observable) eye movements are tightly coupled with covert (unobservable) shifts of visual attention (Fig. 2, O1). Attention and eye movements are guided by the same regions in the brain (Corbetta & Shulman, Reference Corbetta and Shulman2002; Findlay, Reference Findlay2005; Findlay & Gilchrist, Reference Findlay and Gilchrist2003; Appendix 1), and their coupling has been likened to a rubber band (Henderson & Hollingworth, Reference Henderson and Hollingworth1998): “the eyes go where attention goes and attention goes where the eyes go”. Therefore, and because they are subject to (mechanical) measurement errors (Duchowski, Reference Duchowski2003), eye-movement recordings are probabilistic indicators of the location and duration of covert attention (Baddeley & Tatler, Reference Baddeley and Tatler2006).
2.2.2. Task and Strategy Switching
Most real-life decision tasks require the reduction in more than one type of uncertainty (Table 1). Rather than reducing these uncertainties simultaneously, during real-life decision making people switch between attention/decision strategies that each aim at reducing a specific type of uncertainty (Haji-Abolhassani & Clark, Reference Haji-Abolhassani and Clark2013, Reference Haji-Abolhassani and Clark2014; Liechty, Pieters, & Wedel, Reference Liechty, Pieters and Wedel2003; van der Lans, Pieters, & Wedel, Reference van der Lans, Pieters and Wedel2008a; van der Lans et al., Reference van der Lans, Pieters and Wedel2008b; Wedel, Pieters, & Liechty, Reference Wedel, Pieters and Liechty2008). Because the human visual system uses eye movements to acquire information “just in time” when the demands of the current task call for it (Hayhoe & Ballard, Reference Hayhoe and Ballard2005), shifts in these strategies are reflected in the observed scan-path of eye movements (Mayr, Kuhns, & Rieter, Reference Mayr, Kuhns and Rieter2013).
Strategy shifts may occur because of competition between subtasks. Task schemas that drive attentional processes may exert mutually inhibitory effects (Gilbert & Shallice, Reference Gilbert and Shallice2002). Top-down (executive) control may also be involved to selectively activate or deactivate these schemas, depending on which subtask has gained priority (Logan & Gordon, Reference Logan and Gordon2001). Such subconscious task interference and volitional top-down control may both operate at the same time (Kiesel et al., Reference Kiesel, Steinhauser, Wendt, Falkenstein, Jost, Philipp and Koch2010). Strategy switching is thus central to decision making in complex real-life settings (Venkatraman, Payne, & Huettel, Reference Venkatraman, Payne and Huettel2014). We submit that it is necessary for implementing both micro- (eye movement; Fig. 2, O1) and macro-(search and choice; Fig. 2, O3) decisions that facilitate the attainment of the overall task goal. Instances of attentional strategy switching are (1) processing the location versus the identity of objects during target search (van der Lans et al., Reference van der Lans, Pieters and Wedel2008a; Reference van der Lans, Pieters and Wedelb), (2) processing by object across attributes versus by attribute across objects during information search and choice (Shi et al., Reference Shi, Wedel and Pieters2013), (3) systematic versus salience-based attention allocation during target search (van der Lans et al., Reference van der Lans, Pieters and Wedel2008a; Reference van der Lans, Pieters and Wedelb), and (4) habitual versus goal-directed processing during choice (Ursu, Zhang, & Erdem, Reference Ursu, Zhang and Erdem2021). To illustrate, we expand on the first two of these processes, which occur during perceptual (location/identity) and preferential (by attribute/object) decision making, respectively. Sections 3.1 and 3.2 describe these processes in more detail.
First, during perceptual decision making, visual information processing in the human brain takes place in two broad pathways (Glaholt & Reingold, Reference Glaholt and Reingold2011; Ungerleider & Mishkin, Reference Ungerleider and Mishkin1982; Appendix 1), each tailored to reduce a specific type of uncertainty (Table 1). The “what” pathway is involved in identification of objects (faces, hands, people, houses). The “where” pathway is involved in the localization of objects. The “what” (identification) and “where” (localization) pathways give rise to different oculomotor patterns (Bullier, Schall, & Morel, Reference Bullier, Schall and Morel1996; Pannasch & Velichkovsky, Reference Pannasch and Velichkovsky2009; Appendix 1). Activity in the “what” stream tends to produce short saccades (Liechty et al., Reference Liechty, Pieters and Wedel2003; Pannasch & Velichkovsky, Reference Pannasch and Velichkovsky2009), with fixations that cluster in a small number of regions that are deemed informative to the task (Smith & Henderson, Reference Smith and Henderson2009; Wedel et al., Reference Wedel, Pieters and Liechty2008; Yarbus, Reference Yarbus1967). Those short saccades result in repeated fixations on an object, which minimizes working memory load and may be required for target identification and specification of the object in terms of its attributes (Droll & Hayhoe, Reference Droll and Hayhoe2007; Rayner, Smith, Malcolm, & Henderson, Reference Rayner, Smith, Malcolm and Henderson2009; Smith & Henderson, Reference Smith and Henderson2009). Tasks with more complex stimuli (naturalistic versus abstract stimuli) and a higher working memory load (choice versus search tasks) therefore typically result in more and longer fixations (Gould, Reference Gould1973; Orquin & Loose, Reference Orquin and Loose2013). Activity of the “where” stream tends to produce longer saccades that serve to rapidly bring peripheral, salient locations and objects into focus. Eye-tracking research has revealed that people frequently switch back and forth between such “what” and “where” strategies, which, respectively, involve repeated fixations on a small region, and longer saccades between distant regions (Liechty et al., Reference Liechty, Pieters and Wedel2003; Pannasch & Velichkovsky, Reference Pannasch and Velichkovsky2009; Wedel et al., Reference Wedel, Pieters and Liechty2008).
As a second example, during preferential decision making on attribute-by-product matrices, people acquire information using processing-by-attribute or processing-by-product strategies (Bettman, Luce, & Payne, Reference Bettman, Luce and Payne1998; Payne, Bettman, & Johnson, Reference Payne, Bettman and Johnson1993). Attribute-based processing involves extraction of information on a single attribute across multiple products. Such processing involves a low-effort attribute-specification strategy that serves to compare products. Product-based processing involves acquisition of information on a single product across multiple attributes. It is a high-effort strategy which supports the integration of information into an overall expected value or utility (Martinovici, Pieters, & Erdem, Reference Martinovici, Pieters and Erdem2021). Early process-tracing methods such as Mouselab, where participants open and close information cells on an electronic display, suggested that people first use by-attribute processing and then switch to by-product processing before making a choice (Bettman et al., Reference Bettman, Luce and Payne1998). Eye-tracking research initially confirmed that during preferential decisions people first tend to make more inter-product saccades which reflect processing-by-attribute, and then more intra-product saccades which reflect a processing-by-product strategy (Pieters & Warlop, Reference Pieters and Warlop1999). However, rather than reflecting a simple and orderly two-stage process, eye-movement data have demonstrated that people repeatedly switch between these two strategies (Table 1) even during decision-making tasks that last a few minutes at most. People tend to extract information on two or three products in a by-attribute strategy, and on two or three attributes in a by-product strategy, and switch back and forth between these two strategies multiple times before making a choice (Shi et al., Reference Shi, Wedel and Pieters2013).
2.2.3. Bottom–Up Factors
Bottom-up factors residing in the stimulus affect attention processes and thus eye movements (Fig. 2, P3), and exert a large influence especially during object localization. These visual factors have strong effects on attention, comparable in size to those of top-down factors such as task instructions (Orquin et al., Reference Orquin, Lahm and Stojić2021). Basic perceptual features, such as luminance, edges, contours, and colors (Treisman & Gelade, Reference Treisman and Gelade1980; Wolfe, Reference Wolfe1994), are extracted and combined into a salience map, or attention priority map (Fig. 2, I1; Appendix 1) (Itti & Koch, Reference Itti and Koch2001; Itti, Koch, & Niebur, Reference Itti, Koch and Niebur1998; Koch & Ullman, Reference Koch and Ullman1985). The attention priority map represents the conspicuousness of locations in the visual field and guides attention and eye movements (Fig. 2, P3) (Donk & Soesman, Reference Donk and Soesman2010; Treisman & Gelade, Reference Treisman and Gelade1980), because the focus of attention successively shifts to locations on the map with decreasing priority (Foulsham & Underwood, Reference Foulsham and Underwood2008; Parkhurst, Law, & Niebur, Reference Parkhurst, Law and Niebur2002). Perceptual pop-out occurs when a particular location in the visual field stands out due to a basic feature that draws attention almost immediately (Parkhurst et al., Reference Parkhurst, Law and Niebur2002; Treisman & Gelade, Reference Treisman and Gelade1980). Inhibition of return (IOR; Klein, Reference Klein2000; Posner & Cohen, Reference Posner and Cohen1984) encourages exploration of novel locations by temporarily inhibiting the return of the eyes to previously attended locations or objects (Appendix 1).
The global layout of the scene also influences eye movements via what is called contextual guidance (Fig. 2, I2) (Torralba, Oliva, Castelhano, & Henderson, Reference Torralba, Oliva, Castelhano and Henderson2006). The essential meaning of a scene, or its gist, is extracted bottom up based on the spatial distribution of low-level features (Oliva & Schyns, Reference Oliva and Schyns2000; Oliva & Torralba, Reference Oliva and Torralba2006). This process is fast. The gist of a typical scene can be perceived even within a single fixation, in less than 100 msec. (Pieters & Wedel, Reference Pieters and Wedel2012; Rousselet, Joubert, & Fabre-Thorpe, Reference Rousselet, Joubert and Fabre-Thorpe2005), presumably immediately upon exposure to it. Gist perception helps the localization and identification of objects and guides the initial scan-path (Mack, Gauthier, Sadr, & Palmeri, Reference Mack, Gauthier, Sadr and Palmeri2008; Appendix 1).
During search tasks on visual scenes, fixating on the center of the scene first may be optimal for assessing the gist and basic features across the entire visual field (Itti & Koch, Reference Itti and Koch2001; Koch & Ullman, Reference Koch and Ullman1985). This optimal viewing position facilitates subsequent eye movements to salient or informative locations (Tatler, Reference Tatler2007). Therefore, there is a tendency to begin the scan-path close to the center of the image or computer screen on which the scene, for example an advertisement or shopping website (Fig. 1), is presented (Mannan, Ruddock, & Wooding, Reference Mannan, Ruddock and Wooding1995; Parkhurst & Niebur, Reference Parkhurst and Niebur2003; Reinagel & Zador, Reference Reinagel and Zador1999; Tatler, Reference Tatler2007). More generally, the layout of visual displays has been shown to affect information acquisition processes and the direction of the scan-path (Glaholt, Wu, & Reingold, Reference Glaholt, Wu and Reingold2010; Pieters & Warlop, Reference Pieters and Warlop1999; Shi et al., Reference Shi, Wedel and Pieters2013; Fig. 2, I2).
2.2.4. Top–Down Factors
Top-down factors, residing in the person and the task, such as memory (Olivers, Meijer, & Theeuwes, Reference Olivers, Meijer and Theeuwes2006) and goals (Hayhoe & Ballard, Reference Hayhoe and Ballard2005; Pieters & Wedel, Reference Pieters and Wedel2020), affect eye movements in an interplay with bottom-up processes (Fig. 2, P4, P5). Yarbus (Reference Yarbus1967) first showed how eye movements are dramatically directed toward stimuli that are informative for the current task or goal. Attention to visual features the viewer believes to be instrumental for task performance is enhanced, and attention to features that are deemed irrelevant is suppressed, via top-down influences on the attention priority map (Pieters & Wedel, Reference Pieters and Wedel2007; Fig. 2, P5; Appendix 1).
Top-down processes may also be primed by the global layout of a visual scene, which may lead to orderly spatial sequences of eye movements that reflect individuals’ use of systematic search and processing strategies (Monk, Reference Monk1984; Ponsoda, Scott, & Findlay, Reference Ponsoda, Scott and Findlay1995; Spalek & Hammad, Reference Spalek and Hammad2005). These occur, for example, when a natural scene with a horizontal layout of objects or text primes the first fixation to be at the top-left, and the saccades to be predominantly from left to right (Shi et al., Reference Shi, Wedel and Pieters2013).
Practice and time pressure are also key top-down factors (Fig. 2, I4). Practice improves decision performance by making the inhibition of distracting stimuli more efficient. Practice results in (1) improved speed of locating and discriminating targets from distractors, i.e., in faster reduction in location and identity uncertainty, and in (2) shorter fixation durations and thus faster response times (response times during decision tasks are approximately equal to the sum of all fixation durations; van der Lans et al., Reference van der Lans, Pieters and Wedel2021; Zelinsky & Sheinberg, Reference Zelinsky and Sheinberg1997). When making decisions under time pressure, people switch from more complete full-information search strategies to more efficient partial-information search strategies (Pieters & Warlop, Reference Pieters and Warlop1999) which may involve (1) shortening fixation durations, or (2) filtering a subset of the available information by ignoring certain objects or their attributes, or (3) shifting to a different acquisition strategy all together (Fig. 2, P4). Specifically, people may switch from a processing-by-product, characterized by intra-product saccades, to a processing-by-attribute strategy, characterized by inter-product saccades. Individual differences in eye movements may be due to a variety of unobservable states and traits and have been documented in reading, scene viewing, and various types of decision tasks (Fig. 2, I5; e.g., Henderson & Hollingworth, Reference Henderson and Hollingworth1998; Lee & Webb, Reference Lee and Webb2005; Pieters & Wedel, Reference Pieters and Wedel2007; Rayner, Reference Rayner2009; Rutishauser & Koch, Reference Rutishauser and Koch2007; Shen & Palmeri, Reference Shen and Palmeri2016).
2.2.5 Utility/Value
Utility, or subjective value, is a measure of the happiness or satisfaction that consumers get from searching, acquiring and/or experiencing goods and services. Economic decisions are often assumed to be maximizing utility: the best choice outcome provides the highest expected utility to the decision maker (McFadden, Reference McFadden1974). Several dual-system accounts of decision making have been proposed for value learning and value-based decision making (Damasio, Reference Damasio1994; Daw & O’Doherty, Reference Daw and O’Doherty2014; Kahneman, Reference Kahneman2011; Wang, Reference Wang2002), whereby reflexive versus reflective decisions, compensatory versus satisficing decisions, or decisions pertaining to positive versus negative departures from a baseline, are controlled by mutually inhibiting (top-down) systems (Fig. 2, P4).
The empirical association between eye-movement measures of visual attention and value or choice outcomes is well established (Isham & Geng, Reference Isham and Geng2013; Krajbich, Armel, & Rangel, Reference Krajbich, Armel and Rangel2010; Pieters & Warlop, Reference Pieters and Warlop1999; Schotter, Berry, McKenzie, & Rayner, Reference Schotter, Berry, McKenzie and Rayner2010; Shi et al., Reference Shi, Wedel and Pieters2013; Shimojo, Simion, Shimojo, & Scheier, Reference Shimojo, Simion, Shimojo and Scheier2003; Stewart et al., Reference Stewart, Hermens and Matthews2016; Stojić et al., Reference Stojić, Orquin, Dayan, Dolan and Speekenbrink2020). Evidence for the role of attention in choice comes from studies that use statistical mediation analysis to assess the extent to which the effect of visual factors on choice behavior is mediated via visual attention, by calculating their indirect effects through the mediator (Zhang, Wedel, & Pieters, Reference Zhang, Wedel and Pieters2009). Those studies have looked into the effects of visual marketing factors such as package design (Milosavljevic, Navalpakkam, Koch, & Rangel, Reference Milosavljevic, Navalpakkam, Koch and Rangel2012), nutrition information (Bialkova & van Trijp, Reference Bialkova and van Trijp2011), shelf position (Atalay, Bodur, & Rasolofoarison, Reference Atalay, Bodur and Rasolofoarison2012; Chandon, Hutchinson, Bradlow, & Young, Reference Chandon, Hutchinson, Bradlow and Young2009; Chen, Burke, Hui, & Leykin, Reference Chen, Burke, Hui and Leykin2021; Deng, Kahn, Unnava, & Lee, Reference Deng, Kahn, Unnava and Lee2016), assortment (Townsend & Kahn, Reference Townsend and Kahn2013), advertisement displays (Zhang et al., Reference Zhang, Wedel and Pieters2009) and product salience on websites (van der Lans et al., Reference van der Lans, Pieters and Wedel2021). This stream of research has provided consistent evidence that the effects of visual factors on search and choice outcomes are statistically mediated by eye-movement metrics.
One significant top-down effect occurs when a previously rewarded stimulus continues to capture attention automatically even if it is no longer associated with the reward (Fig. 2, P5) (Anderson, Laurent, & Yantis, Reference Anderson, Laurent and Yantis2011; Della Libera & Chelazzi, Reference Della Libera and Chelazzi2006). The learned stimulus-reward association results in an enduring attentional priority and a very slow extinction response (Anderson & Yantis, Reference Anderson and Yantis2013) that hampers suppression of that stimulus during subsequent search and choice for task-relevant stimuli.
Importantly, the relationship between utility and attention is bidirectional (Fig. 1, P1 P2). Despite some alternative accounts (Glaholt & Reingold, Reference Glaholt and Reingold2011), there is converging evidence that people tend to look more at what they like (Fig. 2, P1; Callaway, Rangel, & Griffiths, Reference Callaway, Rangel and Griffiths2021; Gluth, Kern, Kortmann, & Vitali, Reference Gluth, Kern, Kortmann and Vitali2020) and tend to like more what they look at (Fig. 2, P2; Bhatnagar & Orquin, Reference Bhatnagar and Orquin2021; Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020). Shimojo and co-authors (Reference Shimojo, Simion, Shimojo and Scheier2003) first proposed this bidirectional effect as a mechanism for the gaze cascade, which is the rapidly accumulating attention on the chosen alternative just before (500–750 ms) a choice is expressed. The gaze cascade is a robust phenomenon that has been demonstrated to occur in two-alternative perceptual and preferential decision tasks (Glaholt & Reingold, Reference Glaholt and Reingold2009), multi-attribute choice (Atalay et al., Reference Atalay, Bodur and Rasolofoarison2012), gambles (Fiedler & Glöckner, Reference Fiedler and Glöckner2012), and intertemporal decision making (Fig. 2, P1; Fisher, Reference Fisher2021).
3. Perceptual Decision Making: Eye-Movement Models of Search
In target search, people search for a predefined object surrounded by other objects on a visual display (Table 1). Search for a specific perfume on the website in Fig. 1 is an example. Target search may occur before people have made a choice, such as when searching for products to consider buying, or after they made a choice, such as when searching for a product they have earlier decided to buy. In specification search, people search for information on the attributes of an object (Table 1), such as the price, brand name or color, among information about other objects (Moorthy et al., Reference Moorthy, Ratchford and Talukdar1997). We next discuss models of these two types of perceptual decisions (Appendix 2 has modeling details).
3.1. Eye-Movement Models of Target Search
In Hidden Markov Models (HMM), unobserved discrete states that evolve over time according to a Markov Process are assumed to generate the observed eye-movement time series according to some probabilistic model. Over-time variations in the observed eye movements are reflections of these unobserved states and the switches between them. Liechty et al. (Reference Liechty, Pieters and Wedel2003) were among the first to model latent attention states via HMMs to identify shifts between attention strategies that people use during exploratory search upon advertising exposure.
During search for complex targets, people aim to reduce two types of uncertainties: location and identity uncertainties (Ungerleider & Mishkin, Reference Ungerleider and Mishkin1982; Appendix 1; Table 1). They do so by switching over time between two attention states in which one of the two subtasks takes precedence (see Liechty et al., Reference Liechty, Pieters and Wedel2003). The two hidden states, localization and identification, are assumed to follow a Markov process over time. Van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a; Reference van der Lans, Pieters and Wedelb) developed HMMs to uncover the time path of localization and identification states from eye-movement patterns during target search. The models in question specify the location of each fixation, in pixel coordinates, as a spatial point process. The two attention states are identified via parametric assumptions on that process that are specific to each state. The localization state causes long-amplitude saccades and the identification state short-amplitude saccades (Bullier et al., Reference Bullier, Schall and Morel1996; Thompson, Reference Thompson2005; Appendix 1). Eye movements in the localization state are driven by the salience of locations in the visual display (Itti & Koch, Reference Itti and Koch2001; Koch & Ullman, Reference Koch and Ullman1985; Appendix 1). In the model, salience is defined in terms of pixel-level perceptual features, including colors, brightness, and edges. Computer vision techniques are used to extract these features from digital images of the search display, resulting in (RGB or CIELAB) feature values for each pixel. Because the eye only processes detailed information from a region of about two degrees of visual angle around the point of fixation (Appendix 1), a Normal spatial kernel with a width of two degrees is used to smooth these pixel-level variables. The salience map is then represented as a weighted combination of perceptual features, the weights being represented by individual-level model parameters. These parameters are assumed to follow a Normal distribution and are estimated based on the eye-movement data. They capture the effect of top-down factors on attention (Fig. 2, P5). Although some consider salience to be a purely bottom-up stimulus property (Itti & Koch, Reference Itti and Koch2001), its operationalization as a weighted sum of basic features by Van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a; Reference van der Lans, Pieters and Wedelb) is in line with the idea that salience results from activation or inhibition of visual information that is deemed, respectively, relevant or irrelevant, which is a top-down process (Gaspelin & Luck, Reference Gaspelin and Luck2018; Sawaki & Luck, Reference Sawaki and Luck2010). Similar probabilistic formulations of salience had been previously proposed (Baddeley & Tatler, Reference Baddeley and Tatler2006; Rutishauser & Koch, Reference Rutishauser and Koch2007). The Van der Lans et al. target search model provides estimates of individual-level salience maps. Further, in the localization state, factors measured at the level of the display (scene organization or display architecture) and the person (task schemas or scanning habits) drive eye movements (Fig. 2, I2, I5). Systematic eye-movement strategies (Spalek & Hammad, Reference Spalek and Hammad2005) are captured via Markov transition probabilities on the ROIs containing objects to the left and right, or top and bottom, respectively, of the previously fixated ROI. The identification state accommodates the tendency to re-fixate on an object to collect more information on its identity (Smith & Henderson, Reference Smith and Henderson2009; Tatler & Vincent, Reference Tatler and Vincent2009). This model and its extensions (van der Lans et al., Reference van der Lans, Pieters and Wedel2021) incorporates a range of well-documented neuro-psychological processes (Appendix 1).
Top-down modulation of low-level visual processes involves selectively enhancing visual features that are diagnostic for a search task and suppressing features that are non-diagnostic (Desimone & Duncan, Reference Desimone and Duncan1995; Fig. 2, P5; Einhäuser, Rutishauser, & Koch, Reference Einhäuser, Rutishauser and Koch2008; Rutishauser & Koch, Reference Rutishauser and Koch2007). Bayesian formulations that encapsulate top-down information via a hierarchical prior reflect the mechanism involved (Borji, Sihite, & Itti, Reference Borji, Sihite and Itti2014; Lee & Mumford, Reference Lee and Mumford2003; Torralba et al., Reference Torralba, Oliva, Castelhano and Henderson2006). Van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a) manipulate task instructions to enable the decomposition of bottom-up and top-down influences according to such a Bayesian hierarchical structure. Estimation of the model on eye-movement data, collected while participants were searching for brands of laundry detergent on a simulated shopping shelf, revealed that about two thirds of the variation in the salience of products on the shelf was due to bottom-up factors and one third due to top-down factors.
Several components of these search models, such as top-down effects and salience-based and systematic processing, can be used in stand-alone models applied in experiments in which other uncertainties have been strictly controlled for. For example, the relative salience of an object fixated during search can be estimated as the average fixation-weighted Euclidean distance between that object and the target object in the CIELAB color space (van der Lans et al., Reference van der Lans, Pieters and Wedel2021). Such an operationalization of salience encapsulates the extent to which participants fixate on distractors that are similar to the target, with shared color being a dominant source of visual similarity (Rutishauser & Koch, Reference Rutishauser and Koch2007). Results across a range of products (sunglasses, sneakers, perfumes) revealed that search efficiency gains occur via top-down suppression of perceptual features of competing, distractor products rather than by enhancement of the features of the target product (van der Lans et al., Reference van der Lans, Pieters and Wedel2021; Fig. 2, P5).
Recent work has captured the time-dependency of eye movements during search and related perceptual decision tasks via first-order autoregressive (AR) model formulations, rather than via HMMs. In AR models, the observed variable (fixations) depends probabilistically on its own past values. AR formulations have been used to capture time-dependencies in eye movements in Generalized Linear Mixed models by Cho, Brown-Schmidt and Lee (Reference Cho, Brown-Schmidt and Lee2018), and in tree-based Item Response Theory models by Cho, Brown-Schmidt, Boeck and Shen (Reference Cho, Brown-Schmidt, Boeck and Shen2020). These models describe the POR (point of regard) of the eyes during search as a sequence of binary micro-decisions. The neuro-psychological support for such formulations, although not used to motivate the original modeling, may come from such phenomena as inhibition of return (IOR; Castel, Pratt, & Craik, Reference Castel, Pratt and Craik2003), attentional momentum (Pratt, Spalek, & Bradshaw, Reference Pratt, Spalek and Bradshaw1999), and systematic oculomotor tendencies (Spalek & Hammad, Reference Spalek and Hammad2005; Fig. 2, P5). Looking at time dependencies via a hierarchical Bayes logistic regression, Shi and Trusov (Reference Shi and Trusov2021) study how people explore search engine (Google) results. They investigate what part of the results page people look at, whether they scroll, which items they look at, and which item they click on. The results show that the prior scan-path affects these micro-decisions, along with top-down effects of search goals and bottom-up effects of the semantic context and the spatial layout of the page.
3.2. Eye-Movement Models of Specification Search
Research in agricultural and food economics has examined specification search for price, nutrition, sustainability and other attributes of products, packaging, and food labels, as reviewed by Van Loo et al. (Reference Van Loo, Grebitus, Nayga, Verbeke and Roosen2018). The purpose of that research is to understand which perceptual features and abstract attributes of objects influence perceptual (“find the most sustainable products on display”) and preferential decisions (“choose the products that fit your preferences best”). Research in this tradition has explored bottom-up and top-down factors, the latter including for example having “no goal” versus having “general health” or more specific “reduce sodium intake” goals (Oswald, Adhikari, & Mohan, Reference Oswald, Adhikari and Mohan2022). For instance, van Herpen and van Trijp (Reference van Herpen and van Trijp2011) found that pictorial “traffic light” labels improved search for attributes of food more than textual labels did, even when people were not under time pressure. These studies provide descriptions of specification search as it unfolds in daily life.
Eye movements during specification search have also been studied as part of other than pure specification tasks (see Table 1). For example, research has examined visual exploration of so-called retail feature advertisements, which display multiple (price discounted or otherwise featured) products in a single advertisement. Visual exploration of these ads is a mixed target/specification search task (Table 1), during which people aim to reduce uncertainty about whether a preferred product is present and if so, what its attributes are. Pieters, Wedel and Zhang (Reference Pieters, Wedel and Zhang2007) examined such a task with a hierarchical Bayes model to capture the multilevel nature of multiple ads nested in such ad displays. They used measures of the visual distinctiveness of the target (perceptual difference between a target ad and its competitors in terms of the sizes of their ROIs -regions of interest) and the heterogeneity of distractors (perceptual differences among the other, competing ads) as predictor variables. Their results showed, in support of fundamental psychological theories (Duncan & Humphreys, Reference Duncan and Humphreys1989), that target distinctiveness facilitated and distractor heterogeneity hampered search. The modelling results enabled optimizing the organization of the ad display to improve search performance for each of the advertised products. Strategy switching during specification search tasks (Liechty et al., Reference Liechty, Pieters and Wedel2003) has also been studied, for instance during exploration of theme advertisements (Liechty et al., Reference Liechty, Pieters and Wedel2003; Wedel et al., Reference Wedel, Pieters and Liechty2008), word-sentence processing (Simola, Salojärvi, & Kojo, Reference Simola, Salojärvi and Kojo2008), picture viewing (Haji-Abolhassani & Clark, Reference Haji-Abolhassani and Clark2013, 2014), and tracking moving targets (Kim, Singh, Thiessen, & Fisher, Reference Kim, Singh, Thiessen and Fisher2020).
In view of the ubiquity of search and choice behavior by consumers on attribute-by-product displays and the potential costs of errors, the paucity of eye-movement research in this domain is surprising. But, for instance, tracking eye movements on ”balanced score cards” that managers rely on to assess employees (Chen, Jermias, & Panggabean, Reference Chen, Jermias and Panggabean2016) revealed factors that support better accounting decisions. Eye-movement research into search and choice on row-column displays has led to qualitatively different insights than obtained by more traditional process tracing methodologies. Research relying on traditional process tracing methodologies, such as information display boards (e.g., Lohse & Johnson, Reference Lohse and Johnson1996) or one-way mirrors to observe people’s eye movements during decision making (e.g., Russo & Leclerc, Reference Russo and Leclerc1994) initially identified two or three well-ordered sequential stages in preferential decision making (from screening to evaluation, and then to verification). Likewise, eye-tracking studies initially found that in repeated conjoint choice tasks, participants switch from using attribute-based strategies first to product-based strategies later on (Meißner & Decker, Reference Meißner and Decker2010). Research with Hidden Markov Models (HMMs) has amended this orderly, sequential, two or three-stage perspective on search and choice processes. Shi et al. (Reference Shi, Wedel and Pieters2013) used a three-layer Hierarchical Hidden Markov Model (HHMM) to represent eye movements made to acquire information on attribute-by-product matrices. Their model has two hierarchically connected layers of unobserved states, where the transitions between states in each layer are governed by a Markov process. Given the states of the first hidden layer, the output layer describes the eye movements using Markov transition probabilities between ROIs that are defined via a row (attribute)-column (product) spatial grid. The first hidden layer consists of two states that represent the latent by-attribute or by-product information acquisition strategies, given the states of the second layer. That second layer contains states that allow for switching between these first-layer strategies. The second-layer states, the authors speculated, might reflect top-down processes that activate a specific information-acquisition strategy. Notably, findings from the HHMM applied to data about choices between laptops presented on a 12 by 4 row-column display are at variance with some of the received knowledge obtained from traditional process tracing methodologies and descriptive modeling. First, rather than starting with attribute-based search, people tend to start and end with product-based information search, while in between relying on attribute-based search. Second, rather than switching only once or twice between attribute-based and product-based search, people switched many times. Third, the switching patterns between attribute- and product-based processing depended on the orientation of the display (attributes-by-products or products-by-attributes).
In another application, Chuk et al. (Reference Chuk, Chan, Shimojo and Hsiao2020) use a similar two-level HHMM to describe visual information acquisition during choice of one out of two faces. The purpose of the analysis was to identify regions of interest (ROIs) that are unknown in terms of their number, locations, and boundaries, and the saccade patterns between them. The states in the first hidden layer are interpreted as individual-specific ROIs, that is regions on the human face that a participant uses in deciding which face they find more appealing. The second layer of the HHMM captures the transitions between states of the first hidden layer. The fixation locations at the output layer are modelled via a spatial Gaussian distribution. The HHMM was estimated for each individual separately using a (variational) Bayesian approach that determines the optimal number of states automatically. The results reveal two dominant patterns of eye movements. In the first pattern, people fixate on the preferred face sooner, but the accuracy of inferring their final choice from the eye movements is lower. In the second, people transition from exploration to fixating on the preferred face later, but the tendency to fixate on their preferred face is stronger.
4. Preferential Decision Making: Eye-Movement Models of Choice
Models of preferential or value-based decision making in marketing and economics traditionally rely on the assumption that people integrate all available information on attributes of the alternatives to arrive at the value or utility of each choice option (Fig. 2, I3). For instance, in sequential search model in economics (Weitzman, Reference Weitzman1979), people are assumed to first sort choice alternatives in order of expected marginal utility and then sequentially search the options until the expected utility of (examining) the next alternative is less than the current alternative (Moorthy et al., Reference Moorthy, Ratchford and Talukdar1997). During that type of product-based processing, people are assumed to rely on compensatory (Fishbein & Ajzen, Reference Fishbein and Ajzen1975; Von Neumann & Morgenstern, Reference Von Neumann and Morgenstern1947) preference models of a linear additive (subjective expected utility) form. Then, the choice outcome corresponds probabilistically to the alternative with maximum utility among the set of all alternatives. Models of such preferential decisions involve the Multinomial Logit or Probit functional forms, which link utility to decision outcomes (Fig. 2, O3). The Mixed Multinomial Logit model is an extension that accommodates unobserved heterogeneity by allowing its parameters to follow a Normal distribution across individuals.
These assumed processes occur during integration tasks (Table 1), but integration does not necessarily involve utility maximization, nor full information, nor linear compensatory choice rules (McFadden, Reference McFadden1974). In real-life decision making, people use various simplifying strategies and choice heuristics to prevent cognitive overload and to balance search benefits and costs (Kahneman, Reference Kahneman2011). For instance, choice inertia and habitual choice are common for (frequent) low risk, low-involvement decisions. These phenomena can be readily accommodated in choice models through Markov formulations that include the immediate past decision outcome or via an exponentially smoothed average of past decision outcomes (Guadagni & Little, Reference Guadagni and Little1983; Keane, Reference Keane1997). These formulations in essence capture reinforcement learning where the learning rates are prespecified (equal to one) or estimated (Rescorla & Wagner, Reference Rescorla and Wagner1972).
Reflective, non-habitual, decision making is more prevalent for high-involvement products and contexts. But even there, some information, such as specific attribute-alternative combinations or even entire attributes or alternatives, may not be considered at all, because the expected costs of processing outweigh the expected benefits (Sims, Reference Sims2003). Thus, to lower cognitive effort, people use simplifying heuristics that are based on only a part of the available information (Payne, Bettman, & Johnson, Reference Payne, Bettman and Johnson1988; Reference Payne, Bettman and Johnson1992). Examples include satisficing (Simon, Reference Simon1955), lexicographic (Von Neumann & Morgenstern, Reference Von Neumann and Morgenstern1947), and elimination-by-aspects rules (Tversky, Reference Tversky1972). To capture these “boundedly rational” decisions, selection mechanisms have been introduced in choice models to reflect how people narrow down the choice set prior to making a full-information choice. Two-stage nested logit models (McFadden, Reference McFadden1981), joint models of consideration and choice (Roberts & Lattin, Reference Roberts and Lattin1997), and models that account for decision strategy shifts (Swait & Adamowicz, Reference Swait and Adamowicz2001) are examples. Alternatively, latent binary selection indicators have been included into utility functions as moderators of product attributes, to capture a variety of decision heuristics (Gilbride & Allenby, Reference Gilbride and Allenby2004, Reference Gilbride and Allenby2006; Jedidi & Kohli, Reference Jedidi and Kohli2008). Research incorporating eye-movement data in choice models has revealed that people rely on compensatory (maximizing) decision making in some instances (Glöckner & Herbold, Reference Glöckner and Herbold2011), on satisficing rules that involve people attending to alternatives until a satisfactory one is found in other (low-involvement) instances (Stüttgen et al., Reference Stüttgen, Boatwright and Monroe2012), or on hybrid decision strategies that involve a combination of optimal search and satisficing (Reutskaja, Nagel, Camerer, & Rangel, Reference Reutskaja, Nagel, Camerer and Rangel2011).
To structure the burgeoning field of eye-movement research on decision making, we distinguish three categories of approaches, based on whether eye movements are (1) used as explanatory variables to infer what attributes and choice options (products) are processed (Sect. 4.1), (2) used in psychological models as indicators that moderate evidence accumulation (Sect. 4.2), or (3) modeled endogenously along with choice outcomes based on economic principles (Sect. 4.3) (details of the key models are provided in Appendix 2).
4.1. Preferential Decision Models with Eye-Movements as Explanatory Variables
Eye movements have been used as explanatory variables in choice models to capture the information that people use or ignore in making decisions. Inattentional blindness is an automatic phenomenon that occurs when certain objects or attributes of a scene are not noticed (even though they might receive eye fixations) because attention is devoted to another task or object (Mack & Rock, Reference Mack and Rock1998). In the context of multi-attribute choice, attribute inattention (Fig. 2, I3, P5) occurs when certain attributes are not processed (Hensher, Rose, & Greene, Reference Hensher, Rose and Greene2005), and object inattention occurs when one or more alternatives are not considered in the choice decision (Roberts & Lattin, Reference Roberts and Lattin1997). But such inattention can be mitigated. When choice tasks in eye-tracking studies are designed to be incentive compatible, participants utilize up to twenty percent more of the attribute information presented to them (Yang, Toubia, & de Jong, Reference Yang, Toubia and de Jong2018). Nonetheless, to accommodate inattention, eye-movement selection indicators (yes-no fixated) have been used as explanatory variables in choice models, as direct effects (Pieters & Warlop, Reference Pieters and Warlop1999), as moderators of the attributes (part-worths) of products (Balcombe, Fraser, & McSorley, Reference Balcombe, Fraser and McSorley2015; Yegoryan, Guhl, & Klapper, Reference Yegoryan, Guhl and Klapper2020), or as mediators to explain decision outcomes (Chandon et al., Reference Chandon, Hutchinson, Bradlow and Young2009; Pieters & Warlop, Reference Pieters and Warlop1999).
4.2. Psychological Process Models of Preferential Decision Making
A stream of literature in psychology has developed process models of decision making that are calibrated on response times and choice outcomes. Such Sequential Sampling Models (SSM) (Ratcliff, Reference Ratcliff1978; Ratcliff, Van Zandt, & McKoon, Reference Ratcliff, Van Zandt and McKoon1999; Smith & Ratcliff, Reference Smith and Ratcliff2004) assume that evidence (perceptual choice) or utility (preferential choice) on two or more choice alternatives accumulates stochastically, until one alternative has accumulated sufficient evidence to cross a decision threshold. A larger value of the threshold results in more accurate but slower responses. Drift Diffusion Models (DDM) are a special case. In the basic DDM version, the accumulation of evidence on each alternative is described by a Wiener diffusion process (which has independent Gaussian increments). DDMs were originally developed to describe accuracy and latency of two-alternative perceptual decision tasks (Ratcliff, Reference Ratcliff1978; Smith & Ratcliff, Reference Smith and Ratcliff2004; Voss, Nagler, & Lerche, Reference Voss, Nagler and Lerche2013), but have later also been applied to examine preferential decision making (Dutilh & Rieskamp, Reference Dutilh and Rieskamp2016; Summerfield & Tsetsos, Reference Summerfield and Tsetsos2012; Voss, Rothermund, & Voss, Reference Voss, Rothermund and Voss2004).
Commonly, DDMs are fit to preferential decision outcomes assuming an underlying diffusion process according to which a unitary subjective value for each alternative accumulates over time. For example, DDMs have been used to describe choices between pairs of food products using preference ratings for these products provided by participants prior to the choice task as exogenous input (Milosavljevic, Malmaud, Huth, Koch, & Rangel, Reference Milosavljevic, Malmaud, Huth, Koch and Rangel2010). DDMs have been fit to choices among multiple alternatives as well, based on the assumption that the differences in accumulated evidence among them favors one of the options and determines choice. Other SSMs describe multi-alternative choice with multiple diffusion processes, each with their own drift rate, which race until the first one crosses a threshold (Usher & McClelland, Reference Usher and McClelland2001; Usher, Olami, & McClelland, Reference Usher, Olami and McClelland2002).
A critical assumption of traditional DDMs is that visual information uptake is randomly distributed across alternatives. Therefore, these models imply that eye movements are uniformly distributed over alternatives (and attributes), which is similar to the implicit assumption in compensatory decision models that people attend equally to all information in the choice task (Glöckner & Herbold, Reference Glöckner and Herbold2011; Orquin et al., Reference Orquin, Lahm and Stojić2021). Despite some challenges in generalizing DDMs, and SSMs more generally, to multi-alternative preferential choice in realistic contexts (e.g., Mormann & Russo, Reference Mormann and Russo2021), the models provide an important step toward connecting neuro-physiological processes to unobserved preference formation. With a few exceptions (e.g., Satomura, Wedel, & Pieters, Reference Satomura, Wedel and Pieters2014), sequential sampling models have yet received limited attention in the marketing and economics literature as process models for decision making. Nonetheless, the Poisson race model, which also rest on sequential sampling of information during stimulus exposure, has been applied to conjoint choice tasks (Ruan, MacEachern, Otter, & Dean, Reference Ruan, MacEachern, Otter and Dean2008). That model assumes that information signals arrive for each alternative according to a Poisson process (with time-varying rate), until an (integer) threshold is crossed. While that model was fit to only macro-outcomes, choice and latency, Poisson race models for perceptual decisions have used eye-tracking data to express how random chunks of information arrive via eye fixations according to a Poisson process until a threshold is crossed that determines the decision outcome (Wedel & Pieters, Reference Wedel and Pieters2000).
Extensions of DDMs have included eye movements to describe perceptual (Rangelov & Mattingley, Reference Rangelov and Mattingley2020; Tavares, Perona, & Rangel, Reference Tavares, Perona and Rangel2017) and preferential decision-making (Callaway et al., Reference Callaway, Rangel and Griffiths2021; Cavanagh, Wiecki, Kochar, & Frank, Reference Cavanagh, Wiecki, Kochar and Frank2014; Towal, Mormann, & Koch, Reference Towal, Mormann and Koch2013). The key feature of the attentional DDM (aDDM) by Krajbich, Rangel and colleagues (Krajbich et al., Reference Krajbich, Armel and Rangel2010; Krajbich, Lu, Camerer, & Rangel, Reference Krajbich, Lu, Camerer and Rangel2012; Krajbich & Rangel, Reference Krajbich and Rangel2011) is that the information on any alternative accumulates only while the eyes fixate on that alternative. The parameters of the model capture the speed of value accumulation, the bias toward the fixated option, and the error variance.
The initial aDDM predicts that alternatives fixated first and fixated more frequently are more likely to be chosen. Still, it does not allow for effects of bottom-up factors (Fig. 2, I1, I2, P3), nor for effects of the accumulating utility on eye movements (Fig. 2, P2; Mormann & Russo, Reference Mormann and Russo2021). Thus, it assumes the eye-movement process to be exogenous to the preference formation and choice processes, that is, saccades between choice options are assumed to be random, which is at variance which evidence reviewed here. Recent extensions of the aDDM (Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020) allow the accumulated value of an option to increase the likelihood that it will be fixated (Fig. 2, P2). This extended model accounts for various eye-movement patterns, including the first fixation and the evolution of fixations on choice alternatives over time. Likewise, Song, Wang, Zhang and Li (Reference Song, Wang, Zhang and Li2019) have proposed a sequential sampling model in which alternatives with higher (value/utility) uncertainty are more likely to be fixated (Table 1). In their model, eye fixations deliver additional information that reduces the uncertainty about choice alternatives via a Bayesian updating mechanism. It has been shown (Callaway et al., Reference Callaway, Rangel and Griffiths2021) that with Bayesian updating the selection of which alternative to fixate and when to terminate the process can be formulated as a dynamic optimization problem, in which (costly) eye movements are allocated optimally over time to acquire information that reduces uncertainty about the values of the alternatives.
4.3. Economic Models of Preferential Decision Making
Recent models of preferential decision-making aim to predict future choice between multiple alternatives while endogenizing the complete eye-movement process. For example, Martinovici et al. (Reference Martinovici, Pieters and Erdem2021) use not just the final fixations, as in research on the gaze cascade (Shimojo et al., Reference Shimojo, Simion, Shimojo and Scheier2003), or the sum of fixations as in aDDMs, but the entire trajectory of eye movements for each of the choice alternatives to predict preferential decision making in a naturalistic choice task. They develop a joint model of eye movements and choice outcomes that describes the gaze on product ROIs over time as a set of covarying higher-order polynomials. It enables prediction of the final choice from gaze patterns well before the actual choices are implemented, out-of-sample. It is a predictive model, however, that is agnostic about the underlying interplay between attention and preference formation prior to choice.
Researchers have recently applied economic modeling frameworks (Gabaix, Laibson, Moloche, & Weinberg, Reference Gabaix, Laibson, Moloche and Weinberg2006; Moorthy et al., Reference Moorthy, Ratchford and Talukdar1997; Weitzman, Reference Weitzman1979) to eye movements, in order to describe information search and choice for high-involvement products (e.g., laptops, cell phones). These frameworks describe information search as a sequential process with an optimal solution. At each step in the process, a decision maker examines the alternative with the highest utility and stops when the realized utility of that alternative is larger than the expected utility of the next alternative (Ursu et al., Reference Ursu, Zhang and Erdem2021; Yang et al., Reference Yang, Toubia and de Jong2015). Information search in these models is thus determined by the expected value that the next piece of information provides. The models in question simultaneously embed micro- (fixation) and macro- (choice) decisions in a utility maximization, multinomial logit, modeling framework. The models assume that people use Bayesian updating of their prior uncertainty about the value of an attribute level (Table 1) with a noisy chunk of information obtained by fixating a product attribute, resulting in an updated product value. The expected utility is modeled as a weighted sum of the part-utilities of the attribute levels. The utility of search (and thus implicitly its cost) is specified as a function of eye-movement characteristics, such as the saccade length and direction (Ursu et al., Reference Ursu, Zhang and Erdem2021; Yang et al., Reference Yang, Toubia and de Jong2015) to allow for local clusters of fixations and for horizontal and vertical saccade tendencies. Unobserved heterogeneity in the models’ parameters across individuals is accommodated via a Normal distribution. The results of that research show that integrating eye movements into models of search and choice improves parameter estimates, the understanding of the choice process, as well as out-of-sample predictions.
The appeal of such economic approaches is that they (1) integrate choice and eye-movement decisions in a single framework, (2) postulate a plausible economic (cost-benefit) mechanism for eye-movement decisions (Callaway et al., Reference Callaway, Rangel and Griffiths2021), and (3) assume that utility/value evolves during the decision process and affects fixations (Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020; Ursu et al., Reference Ursu, Zhang and Erdem2021). However, a limitation of current implementations is that known influences of visual factors and attentional processes (Fig. 2, bottom up: I1, I2, P3, and top down: I4, P4, P5) are not accommodated or only in a basic way. Also, the assumed (one-step) forward-looking mechanism remains as yet unverified.
Research for low-involvement value-based decisions (e.g., snacks) has also relied on an utility framework, but has specified different underlying processes (Reutskaja et al., Reference Reutskaja, Nagel, Camerer and Rangel2011; Stüttgen et al., Reference Stüttgen, Boatwright and Monroe2012). For low-involvement decisions, target search is more likely a main component of the choice task (Table 1), with people relying on the perceptual salience of objects, habitual decision making, and satisficing choice rules. For instance, in modeling choice of one out of a large set of products under time pressure, it was assumed that people may stop and choose after having fixated all alternatives at least once or after running out of time (Reutskaja et al., Reference Reutskaja, Nagel, Camerer and Rangel2011). This assumption is in line with a satisficing choice heuristic where search stops after the value of the currently fixated alternative exceeds a reservation value.
Stüttgen et al. (Reference Stüttgen, Boatwright and Monroe2012) extended the target search model of van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a) by including a third state in the HMM, in addition to the localization and identification states. The model specifies a satisficing rather than maximizing process (Simon, Reference Simon1955). Specifically, in the third, termination state an individual chooses a product that is satisfactory, as follows (products that are undetermined are chosen with a probability close to zero). The individual assigns the status satisfactory, unsatisfactory, or undetermined to each product at each fixation. If a product (here, instant noodles) has not been fixated, its status is undetermined. To determine whether a product is satisfactory, the individual needs to fixate all attributes of that product and the value of each attribute needs to be acceptable. The model accounts for strategy switching, where the switching probabilities depend on the status of the products and the number of prior fixations. It allows people to proceed to a new choice option before returning and making a final choice, however, which is at variance with a pure satisficing heuristic (Gilbride & Allenby, Reference Gilbride and Allenby2004, Reference Gilbride and Allenby2006; Jedidi & Kohli, Reference Jedidi and Kohli2008) or the process assumed in aDDMs (Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020; Krajbich et al., Reference Krajbich, Armel and Rangel2010; Song et al., Reference Song, Wang, Zhang and Li2019).
5. Conclusions and Opportunities for Future Research
Eye movements offer a unique window on perceptual, cognitive, and evaluative processes of people who are engaged in decision making tasks. They afford tests of fundamental theories, new insights into search and choice phenomena, and predictions of future decisions. Understanding how complex decisions are made in real life requires recognizing that real-life decision tasks are mixtures of elementary tasks through which people try to reduce multiple uncertainties (Table 1). Therefore, a key component of our framework in Table 1 and Fig. 2 is the idea that people switch between strategies to reduce the multiple uncertainties inherent to complex decision tasks. In addition, the execution of these tasks is subject to a myriad of bottom-up and top-down factors that influence the perceptual, cognitive, and evaluative processes that drive observable micro- (eye movements) and macro- (choice) decision outcomes (Fig. 1). Psychometric, econometric, and statistical models of these micro- and macro-decisions have been developed for somewhat different decision-making contexts and are therefore based on different assumptions tailored to these contexts. To advance insights into search and choice, a synthesis of these models is called for. The present review aims to provide a first step toward such a synthesis, and the research agenda that we propose next serves that purpose.
First, while existing eye-movement models of target (van der Lans et al., Reference van der Lans, Pieters and Wedel2008a; Reference van der Lans, Pieters and Wedelb; Reference van der Lans, Pieters and Wedel2021) and specification search (Shi et al., Reference Shi, Wedel and Pieters2013) capture perceptual decision tasks (Table 1) relatively accurately, there are opportunities to improve upon them. Extant models of target and specification search are disconnected and cannot directly be used to predict choice outcomes, which presents an opportunity for future research. In addition, these models have relied on a priori specified perceptual features and regions of interest (ROIs). Further research can establish whether such prespecified variables most accurately capture the visual inputs that people use to process information during perceptual decision tasks. Advances in computer vision and machine learning could be used to (automatically) extract a large variety of characteristics of images, video, and text. Furthermore, eye-movement patterns themselves can be used to extract ROIs that are relevant for the decision task at hand (Chuk et al., Reference Chuk, Chan, Shimojo and Hsiao2020). Those data could be used in learning models (Ursu et al., Reference Ursu, Zhang and Erdem2021; Yang et al., Reference Yang, Toubia and de Jong2015) to better understand what information people use during identification and specification processes (see Table 1). Further, the rich body of knowledge on eye movements during reading (Rayner, Reference Rayner1998; Rayner, Schotter, Masson, Potter, & Treiman, Reference Rayner, Schotter, Masson, Potter and Treiman2016) may inform future studies that aim to refine models of people’s information acquisition from text during decision making.
Second, there are opportunities to extend DDMs and, similarly, SSMs. These models have been used to fit preferential decisions by postulating mechanisms of how the accumulation of evidence reduces decision uncertainty, similar to those for perceptual decision making (Callaway et al., Reference Callaway, Rangel and Griffiths2021; Dutilh & Rieskamp, Reference Dutilh and Rieskamp2016). Several directions for improved theorizing and modeling remain: (1) extant research often infers the plausibility of the underlying sequential sampling processes from the statistical fit between inputs and outputs, rather than by examining the processes directly through eye movements. (2) DDMs typically rely on the assumption that visual information uptake is uniformly distributed across alternatives and attributes (for an exception see Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020). This assumption is at variance with evidence that attention tends to be directed to higher valued options or the emerging winner during choice tasks (Martinovici et al., Reference Martinovici, Pieters and Erdem2021; Meißner, Musalem, & Huber, Reference Meißner, Musalem and Huber2016; Pieters & Warlop, Reference Pieters and Warlop1999; Shimojo et al., Reference Shimojo, Simion, Shimojo and Scheier2003). (3) Preferences are often assumed to be fixed and are measured prior to the decision task. The drift in a DDM is then to be interpreted as the accumulation of information on those preferences retrieved from memory (Milosavljevic et al., Reference Milosavljevic, Malmaud, Huth, Koch and Rangel2010). While this simplification may provide a reasonable description of habitual, perceptual decision making, it hampers the successful application of DDMs to high-involvement, preferential choice contexts in which perceived utility of choice options and eye movements toward them may interact. The attentional DDM takes a step forward by incorporating eye movements into the value-accumulation process (Krajbich et al., Reference Krajbich, Armel and Rangel2010), but the mechanism driving eye movements is still mostly assumed exogenous (Mormann & Russo, Reference Mormann and Russo2021). In addition, the assumption that all attention reflects or adds positive utility requires tests in contexts where people attend to negative outcomes to avoid. More research is thus needed on the dynamic interplay of attention and value accumulation in DDMs (Fig. 2, P1 and P2), also because that interplay causes violations of IIA decision making (Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020). IIA (Independence of Irrelevant Alternatives) specifies, restrictively, that the ratio of choice probabilities between two alternatives should not depend on the presence of a third alternative (Louie, Khaw, & Glimcher, Reference Louie, Khaw and Glimcher2013; Luce, Reference Luce1977). Recent work that extends the aDDM by formulating the probability that an alternative is fixated as a (logistic) function of its accumulated value (Gluth et al., Reference Gluth, Kern, Kortmann and Vitali2020) holds promise. Further, research is needed to alleviate the assumption in extant DDMs that decisions are based on accumulation of a unitary subjective value, by allowing for representations of multi-attribute decision making similar to those in economic models of choice. Some DDMs for perceptual decisions already incorporate such formulations. For example, Noguchi and Stewart (Reference Noguchi and Stewart2018) propose an evidence accumulation model based on observations from process-tracing and eye-movement models in which decisions are based on the accumulation of pairwise comparisons of attributes.
Third, econometric models of search and choice assume that people are forward looking and make a tradeoff between choosing now based on the available information or using eye movements to search for more information and then making a decision (Ursu et al., Reference Ursu, Zhang and Erdem2021; Yang et al., Reference Yang, Toubia and de Jong2015). The key assumption that people are (one-step ahead) forward looking when making mostly subconscious eye movements remains to be verified, however. That assumption might hold for high-involvement contexts involving specification search, but less so in low-involvement contexts where target search dominates preferential choice. A further limitation of current econometric applications is that several key attention processes (Fig. 2, P3 and P5) are not considered or are included via fairly restrictive assumptions. For example, visual factors, which have a large impact on choice decisions (Orquin et al., Reference Orquin, Lahm and Stojić2021), are typically absent. Extant models do not account for consecutive refixations on the same object (Chandon et al., Reference Chandon, Hutchinson, Bradlow and Young2009; Krajbich et al., Reference Krajbich, Armel and Rangel2010; Martinovici et al., Reference Martinovici, Pieters and Erdem2021; Yang et al., Reference Yang, Toubia and de Jong2015), which is a striking characteristic of scan-paths across a wide range of tasks (Liechty et al., Reference Liechty, Pieters and Wedel2003; Musalem, Montoya, Meißner, & Huber, Reference Musalem, Montoya, Meißner and Huber2021; Rayner, Reference Rayner1998; van der Lans et al., Reference van der Lans, Pieters and Wedel2008b).
Fourth, despite the different approaches taken in the models developed in psychology, marketing and economics, there are also some remarkable similarities. As a case in point, econometric (random utility) choice models and some SSMs used in psychology are mathematically equivalent (Webb, Reference Webb2019). Further, the threshold-crossing phenomena in SSMs resemble satisficing (Glimcher, Reference Glimcher2010; Reutskaja et al., Reference Reutskaja, Nagel, Camerer and Rangel2011; Stüttgen et al., Reference Stüttgen, Boatwright and Monroe2012). DDMs are mathematically equivalent to Bayesian decision models (Bitzer, Park, Blankenburg, & Kiebel, Reference Bitzer, Park, Blankenburg and Kiebel2014). The Bayesian updating mechanism by which fixations reduce uncertainty in process models in psychology (Callaway et al., Reference Callaway, Rangel and Griffiths2021; Song et al., Reference Song, Wang, Zhang and Li2019) is almost identical to the mechanism that has been assumed in models of search and choice in marketing and economics (Ursu et al., Reference Ursu, Zhang and Erdem2021; Yang et al., Reference Yang, Toubia and de Jong2015). Finally, the hierarchical Bayesian priors that have been used in psychology and computer vision to capture top-down influences on eye-movements (Borji et al., Reference Borji, Sihite and Itti2014; Torralba et al., Reference Torralba, Oliva, Castelhano and Henderson2006) are identical to those implemented in statistical models of search in marketing (van der Lans et al., Reference van der Lans, Pieters and Wedel2008a). Such similarities in approaches developed in rather independent streams of research not only reveal convergent validity of assumptions underlying different models, but also provide touchpoints to further integrate models from psychology, economics, and marketing. This review has tried to lay a foundation for such an integration by incorporating the elementary tasks and cognitive processes involved in perceptual and preferential decision making in a single conceptual framework (Table 1; Fig. 2).
Fifth, more theoretical and empirical work on the role of tasks and task switching in search and choice is called for. We have noted that decisions in real-life contexts comprise of elementary subtasks (Table 1) that may, for example, involve both target search and specification search, or habitual and reflective decision making. Future research could integrate mathematical representations of these processes by capitalizing on representations of task/strategy switching and existing communalities between model formulations. Strategy switching has already been demonstrated for micro-decisions in a wide range of tasks (Chuk et al., Reference Chuk, Chan, Shimojo and Hsiao2020; Shi et al., Reference Shi, Wedel and Pieters2013; Stüttgen et al., Reference Stüttgen, Boatwright and Monroe2012; van der Lans et al., Reference van der Lans, Pieters and Wedel2008a; Reference van der Lans, Pieters and Wedelb; Wedel et al., Reference Wedel, Pieters and Liechty2008). Whereas dual-process theories for macro-decisions abound (Damasio, Reference Damasio1994; Glimcher, Reference Glimcher2010; Kahneman, Reference Kahneman2011), and initial evidence for extensive strategy switching during these decisions comes from eye movement recordings (Venkatraman et al., Reference Venkatraman, Payne and Huettel2014), more work is awaited that incorporates strategy switching in psychological (SSM) and econometric (sequential search) models and applies these to more fully understand how people switch between decision strategies, for example based on cost-benefit tradeoffs (Payne et al., Reference Payne, Bettman and Johnson1988; Venkatraman et al., Reference Venkatraman, Payne and Huettel2014).
In closing, the study of search and choice in natural conditions requires strong theory as well as sound psychometric, econometric, and statistical models to infer the underlying perceptual, cognitive and evaluative processes. Marketing and economics have provided a fruitful testing ground for theories and models of attention and decision making, because of their focus on consumer decision making toward complex pictorial and textual, static, dynamic, and multisensory stimuli in natural contexts. Eye-movement data have come to play a critical role. Naturally, therefore, research, product and service companies have embraced eye tracking as a tool. With eye tracking via regular webcams being a low-cost option, eye-movement recording is already implemented in smart phones, car navigation, and head-mounted virtual reality devices. Measures produced as a by-product of eye movement recording, such as fixation durations, micro-saccades, distance between eye and stimulus, pupil dilations, and facial expressions of emotions, could be further exploited (Pieters & Wedel, Reference Pieters and Wedel2020). Given those developments, understanding, predicting, and improving decision making in practice would benefit greatly from adopting the models reviewed here, and the extensions and generalizations that we hope the proposed framework stimulates.
Acknowledgements
The authors are grateful to Jacob Orquin for very useful comments on this manuscript.
Appendix 1: Neural Foundations of Eye Movements During Search and Choice
Light is projected through the cornea and the lens of the eye, on the retina. The photoreceptors in the retina process color (cones; in the fovea), luminance (rods; in the periphery) and contrast (bipolar and ganglion cells), amongst others. Via the fovea, the eye extracts high-acuity information from a region of about 2 degrees of visual angle (Palmer, Reference Palmer1999). Signals from the retina are sent via the optic nerve to the Lateral Geniculate Nuclei (LGN; in the Thalamus). From there on information of the two eyes is combined and passed (via the optic radiation) to area V1 in the Occipital Lobe. The visual areas in this lobe form a hierarchy and specialize in the processing of low-level visual features, such as edges (V1, V2), depth (V2), contours (V2), simple shapes (V4), colors (V4), and self-(V5), and object (V6) motion. These areas are organized as retinotopic maps.
The basic perceptual features that are processed bottom-up, pre-attentively via areas V1-V4 (Treisman & Gelade, Reference Treisman and Gelade1980; Wolfe, Reference Wolfe1994) are combined to form a salience map (Itti & Koch, Reference Itti and Koch2001; Itti et al., Reference Itti, Koch and Niebur1998; Koch & Ullman, Reference Koch and Ullman1985). The salience map is a retinotopic map that represents the conspicuity of locations in the visual field. It is represented in V1, the Superior Colliculus (SC) and the Frontal Eye Fields (FEF) (Koch & Ullman, Reference Koch and Ullman1985; Niebur & Koch, Reference Niebur and Koch1998; Treue, Reference Treue2003), where its representation may be short-lived (Donk & Soesman, Reference Donk and Soesman2010).
These areas V1-V6 output information via two streams, the ventral (“what”) and the dorsal (“where”) stream (Ungerleider & Mishkin, Reference Ungerleider and Mishkin1982). The ventral stream processes mostly foveal information, connects to the Inferotemporal Cortex (ITC) and is concerned with object recognition (Bar, Reference Bar2004). The ITC projects into the Perirhinal Cortex and Hippocampus amongst others, which are involved in memory, and into the Prefrontal Cortex (PFC). The PFC is involved in planning and reflective goal-directed decisions, while the (dorsolateral) striatum is involved in habitual or reflexive decisions; both regions are thought to encode value (Daw & O’Doherty, Reference Daw and O’Doherty2014; Glimcher, Reference Glimcher2010).
The top-down influence of goals, for example, originates in the PFC (Desimone & Duncan, Reference Desimone and Duncan1995), while value-driven attentional capture, whereby stimuli associated with a reward attract attention involuntarily, involves dopamine production (which confers motivational salience) from the basal ganglia (Berridge, Reference Berridge2012; Hayhoe & Ballard, Reference Hayhoe and Ballard2005). Top-down influences occur along the entire visual hierarchy in areas V1-V5, ITC, SC, and PPC (Corbetta & Shulman, Reference Corbetta and Shulman2002; Tipper, Weaver, & Houghton, Reference Tipper, Weaver and Houghton1994) and enhance task-relevant and suppress task-irrelevant features and objects (Sawaki & Luck, Reference Sawaki and Luck2010).
The dorsal stream processes spatial information mostly from the peripheral retina and is connected to the Posterior Parietal Cortex (PPC) which is involved in the location of and planning of action toward objects and in integrating sensory information. The Retrosplenial Cortex (RSC) holds a representation of scenes based on coarse global information and activates scene schemas in the Parahippocampal Cortex (PHC; Bar, Reference Bar2004). The PHC primes specific object representations in the ITC (Bar, Reference Bar2004) and is thereby responsible for contextual guidance of eye movements.
The SC and FEF are involved in the production of eye movements. The SC receives input directly from the LGN and directs the eyes to salient locations. The FEF direct eye movements to remembered stimuli and are involved in both the facilitation of voluntary saccades and in the inhibition of reflexive saccades that originate in the SC (Rafal, Machado, Ro, & Ingle, Reference Rafal, Machado, Ro and Ingle2000). Specific areas of the SC and FEF that are part of the dorsal stream are involved in long-amplitude saccades, whereas other areas of the SC and FEF that are part of the ventral stream produce short-amplitude saccades (Bullier et al., Reference Bullier, Schall and Morel1996; Thompson, Reference Thompson2005). The SC is also involved in the Inhibition of Return (IOR; Sapir, Soroker, Berger, & Henik, Reference Sapir, Soroker, Berger and Henik1999), which temporarily inhibits the return of the eyes to previously attended locations or objects (Castel et al., Reference Castel, Pratt and Craik2003).
Appendix 2: Details of Selected Search and Choice Models
This appendix details some of the models described in the main text, using the following notation. At time t, a visual scene is comprised of coordinates
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( l_{1},l_{2} \right) $$\end{document}
![]() , with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$l_{1}=1,..,L_{1}$$\end{document}
, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$l_{1}=1,..,L_{1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$l_{2}=1,..,L_{2}\mathrm {.}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$l_{2}=1,..,L_{2}\mathrm {.}$$\end{document}
![]() Image content is given by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {M}_{\mathrm {kt}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
Image content is given by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {M}_{\mathrm {kt}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {k=1,\ldots ,K}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {k=1,\ldots ,K}$$\end{document}
![]() , for K visual features, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {h\, =\, 1,\ldots ,H}$$\end{document}
, for K visual features, and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {h\, =\, 1,\ldots ,H}$$\end{document}
![]() ROIs with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{ht}\left( l_{1},l_{2} \right) =1$$\end{document}
ROIs with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{ht}\left( l_{1},l_{2} \right) =1$$\end{document}
![]() if location
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( l_{1},l_{2} \right) $$\end{document}
if location
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( l_{1},l_{2} \right) $$\end{document}
![]() falls into ROI h at time t, and zero otherwise. If the images are stationary, the subscript t is dropped. The vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {x}_{\mathrm {i,t}}=\left( l_{1},l_{2} \right) $$\end{document}
falls into ROI h at time t, and zero otherwise. If the images are stationary, the subscript t is dropped. The vector
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {x}_{\mathrm {i,t}}=\left( l_{1},l_{2} \right) $$\end{document}
![]() represents the location of fixation t for individual i. The entire scan-path is denoted as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {x}_{\mathrm {i,1:T}}$$\end{document}
represents the location of fixation t for individual i. The entire scan-path is denoted as
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {x}_{\mathrm {i,1:T}}$$\end{document}
![]() .
.
5.1. Model of Target Search
Using a spatial point process, van der Lans et al. (Reference van der Lans, Pieters and Wedel2008b) model the location of each fixation t for person i in image-pixel coordinates
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( l_{1},l_{2} \right) {.\, }$$\end{document}
![]() The explanatory variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {itj}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
The explanatory variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {itj}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() ,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {j=1,...,J}$$\end{document}
,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {j=1,...,J}$$\end{document}
![]() are features
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {M}_{\mathrm {k}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
are features
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {M}_{\mathrm {k}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() and ROIs of packages or text of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {m\, =\, 1,..,M}$$\end{document}
and ROIs of packages or text of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {m\, =\, 1,..,M}$$\end{document}
![]() brands, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{m}^{pack}\left( l_{1},l_{2} \right) =1$$\end{document}
brands, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{m}^{pack}\left( l_{1},l_{2} \right) =1$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{m}^{text}\left( l_{1},l_{2} \right) =1$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{m}^{text}\left( l_{1},l_{2} \right) =1$$\end{document}
![]() if location
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( l_{1},l_{2} \right) $$\end{document}
if location
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left( l_{1},l_{2} \right) $$\end{document}
![]() falls into the package or text. The individual-specific effects
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,j\, }}$$\end{document}
falls into the package or text. The individual-specific effects
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,j\, }}$$\end{document}
![]() of each explanatory variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {itj}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
of each explanatory variable
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {itj}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() depend on whether that person is in the localization or in the identification state. The HMM likelihood of the entire scan-path
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {x}_{\mathrm {i,1:T}}$$\end{document}
depend on whether that person is in the localization or in the identification state. The HMM likelihood of the entire scan-path
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {x}_{\mathrm {i,1:T}}$$\end{document}
![]() of individual
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {i}$$\end{document}
of individual
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {i}$$\end{document}
![]() is:
is:

where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }_{\mathrm {s}}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Sigma }_{\mathrm {s}}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Sigma }_{\mathrm {s}}$$\end{document}
![]() are the mean and covariance matrix of the multivariate Normal heterogeneity distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,s\, }}$$\end{document}
are the mean and covariance matrix of the multivariate Normal heterogeneity distribution of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,s\, }}$$\end{document}
![]() . The Markov transition probabilities between the localization and identification states are:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppi }_{s_{t}{|}s_{t-1}}$$\end{document}
. The Markov transition probabilities between the localization and identification states are:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppi }_{s_{t}{|}s_{t-1}}$$\end{document}
![]() , with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_{t}\in \left\{ 1,2 \right\} ;\, {\uppi }_{\mathrm {s}_{\mathrm {2}}{|}\mathrm {s}_{1}}={\uppi }_{\mathrm {1}}$$\end{document}
, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$s_{t}\in \left\{ 1,2 \right\} ;\, {\uppi }_{\mathrm {s}_{\mathrm {2}}{|}\mathrm {s}_{1}}={\uppi }_{\mathrm {1}}$$\end{document}
![]() represent the initial state probabilities. The vector of explanatory variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {it,s}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
represent the initial state probabilities. The vector of explanatory variables
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {it,s}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() for the localization state (s
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$=$$\end{document}
for the localization state (s
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$=$$\end{document}
![]() 1) are, first, pixel-level features
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {M}_{k}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
1) are, first, pixel-level features
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {M}_{k}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() . Second, systematic strategies are captured via
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {left-right(}x}_{i,t-1})}^{pack}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) \, $$\end{document}
. Second, systematic strategies are captured via
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {left-right(}x}_{i,t-1})}^{pack}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) \, $$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {top-bottom(}x}_{i,t-1})}^{pack}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) \, $$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {top-bottom(}x}_{i,t-1})}^{pack}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) \, $$\end{document}
![]() which represent the ROIs to the left and right, or top and bottom, respectively, of the previously fixated package. Third, in the identification state (s
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$=$$\end{document}
which represent the ROIs to the left and right, or top and bottom, respectively, of the previously fixated package. Third, in the identification state (s
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$=$$\end{document}
![]() 2) the tendency to re-fixate on a text or package ROI is captured via
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {refix(}x}_{i,t-1})}^{pack}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) \, $$\end{document}
2) the tendency to re-fixate on a text or package ROI is captured via
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {refix(}x}_{i,t-1})}^{pack}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) \, $$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {refix(}x}_{i,t-1})}^{text}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{{\mathrm {refix(}x}_{i,t-1})}^{text}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() . The probability of fixating on a location is:
. The probability of fixating on a location is:

with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {a}_{it,s}\left( \mathrm {l}_{\mathrm {1}}, \mathrm {l}_{\mathrm {2}} \right) ={\mathrm {V}_{\mathrm {it,s}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) }^{'}{\uptheta }_{\mathrm {i,s\, }}$$\end{document}
![]() . Here,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {it,1}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
. Here,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {it,1}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() contains all explanatory variables and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {it,2}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
contains all explanatory variables and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {V}_{\mathrm {it,2}}\left( \mathrm {l}_{\mathrm {1,}}, \mathrm {l}_{\mathrm {2}} \right) $$\end{document}
![]() the variables that affect identification. van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a) extend the model by including top-down influences on salience, via a between-subjects experiment with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {g(i)\, =\, 1,\ldots ,G}$$\end{document}
the variables that affect identification. van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a) extend the model by including top-down influences on salience, via a between-subjects experiment with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {g(i)\, =\, 1,\ldots ,G}$$\end{document}
![]() search goals of participant i as experimental conditions. The individual-level parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,1:K\, }}$$\end{document}
search goals of participant i as experimental conditions. The individual-level parameters
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,1:K\, }}$$\end{document}
![]() can then be decomposed into bottom-up (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu )}$$\end{document}
can then be decomposed into bottom-up (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu )}$$\end{document}
![]() and top-down
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {(}{\upmu }_{\mathrm {g(i)}})$$\end{document}
and top-down
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {(}{\upmu }_{\mathrm {g(i)}})$$\end{document}
![]() influences, according to a hierarchical structure,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,1:K,\, s=1\, }}{\sim N}\left( {\upmu +}{\upmu }_{\mathrm {g(i)}}, {\Sigma }_{\mathrm {s=1}} \right) $$\end{document}
influences, according to a hierarchical structure,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uptheta }_{\mathrm {i,1:K,\, s=1\, }}{\sim N}\left( {\upmu +}{\upmu }_{\mathrm {g(i)}}, {\Sigma }_{\mathrm {s=1}} \right) $$\end{document}
![]() , with Normal priors on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }$$\end{document}
, with Normal priors on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }_{\mathrm {g(i)}}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }_{\mathrm {g(i)}}$$\end{document}
![]() and a Wishart prior on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Sigma }_{\mathrm {s=1}}$$\end{document}
and a Wishart prior on
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\Sigma }_{\mathrm {s=1}}$$\end{document}
![]() .
.
5.2. Model of Specification Search
Shi et al. (Reference Shi, Wedel and Pieters2013) propose a three-layer HHMM to analyze specification search, which involves three sets of Markovian transition probabilities:
-
The transition probabilities between higher order states, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathrm {R}_{\mathrm {t}}$$\end{document}
 , of the upper layer,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppi }_{\mathrm {R}_{\mathrm {t}}{|}\mathrm {R}_{\mathrm {t-1}}}$$\end{document}
, of the upper layer,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppi }_{\mathrm {R}_{\mathrm {t}}{|}\mathrm {R}_{\mathrm {t-1}}}$$\end{document}

-
The transition probabilities between the two states, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathrm {S}_{\mathrm {t}}$$\end{document}
 , of the middle layer that represent by-attribute and by-product processing, given the states of the upper layer,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppi }_{\mathrm {S}_{\mathrm {t}}{|}\mathrm {S}_{\mathrm {t-1}}}^{\mathrm {R}_{t}}$$\end{document}
, of the middle layer that represent by-attribute and by-product processing, given the states of the upper layer,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppi }_{\mathrm {S}_{\mathrm {t}}{|}\mathrm {S}_{\mathrm {t-1}}}^{\mathrm {R}_{t}}$$\end{document}
 .
. -
The probabilities of eye movements between cells on the display given the states of the middle layer \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\mathrm {P}^{\mathrm {S}_{\mathrm {t}}}\left( \mathrm {x}_{\mathrm {i,t}}{|}\mathrm {x}_{\mathrm {i,t-1}} \right) $$\end{document}
 . Here,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {P}^{1}\left( \mathrm {x}_{\mathrm {i,t}}{|}\mathrm {x}_{\mathrm {i,t-1}} \right) $$\end{document}
. Here,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {P}^{1}\left( \mathrm {x}_{\mathrm {i,t}}{|}\mathrm {x}_{\mathrm {i,t-1}} \right) $$\end{document}
 is a function of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{\mathrm {attr}\left( \mathrm {x}_{\mathrm {i,t-1}} \right) }\left( \mathrm {x}_{\mathrm {i,t}} \right) ,$$\end{document}
is a function of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{\mathrm {attr}\left( \mathrm {x}_{\mathrm {i,t-1}} \right) }\left( \mathrm {x}_{\mathrm {i,t}} \right) ,$$\end{document}
 attribute ROIs, capturing a by-attribute tendency and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {P}^{2}\left( \mathrm {x}_{\mathrm {i,t}}{|}\mathrm {x}_{\mathrm {i,t-1}} \right) $$\end{document}
attribute ROIs, capturing a by-attribute tendency and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {P}^{2}\left( \mathrm {x}_{\mathrm {i,t}}{|}\mathrm {x}_{\mathrm {i,t-1}} \right) $$\end{document}
 a function of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{\mathrm {prod}\left( \mathrm {x}_{\mathrm {i,t-1}} \right) }\left( \mathrm {x}_{\mathrm {i,t}} \right) \, $$\end{document}
a function of
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{\mathrm {prod}\left( \mathrm {x}_{\mathrm {i,t-1}} \right) }\left( \mathrm {x}_{\mathrm {i,t}} \right) \, $$\end{document}
 , product ROIs capturing a by-product tendency.
, product ROIs capturing a by-product tendency.
The full HHMM model likelihood is:

5.3. DDM of Preferential Decision Making
The attentional DDM (aDDM) (Krajbich et al., Reference Krajbich, Armel and Rangel2010; Krajbich et al., Reference Krajbich, Lu, Camerer and Rangel2012; Krajbich & Rangel, Reference Krajbich and Rangel2011) specifies that the rate of accumulation (drift) of the decision value depends on the product or price ROI that the eyes fixate on. Alternative j is selected if its accumulated value
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {v}_{ijt}$$\end{document}
![]() is the first to cross some threshold
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{i}$$\end{document}
is the first to cross some threshold
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{i}$$\end{document}
![]() :
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {Y}_{\mathrm {i}}\mathrm {=j,\, if} \quad \left| \mathrm {v}_{ijt} \right| >\tau _{i}$$\end{document}
:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {Y}_{\mathrm {i}}\mathrm {=j,\, if} \quad \left| \mathrm {v}_{ijt} \right| >\tau _{i}$$\end{document}
![]() , with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left| \mathrm {v}_{ikt} \right| \le \tau _{i}\, \forall k=1,..,J\cap k\ne j$$\end{document}
, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left| \mathrm {v}_{ikt} \right| \le \tau _{i}\, \forall k=1,..,J\cap k\ne j$$\end{document}
![]() . A larger value of the threshold
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{i}$$\end{document}
. A larger value of the threshold
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\tau _{i}$$\end{document}
![]() result in more accurate but slower responses. For a product fixation, the drift is:
result in more accurate but slower responses. For a product fixation, the drift is:
for a price fixation the drift is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$-{\upphi }\left( \mathrm {z}_{2}\mathrm {-\beta }\mathrm {z}_{1} \right) $$\end{document}
![]() . Here,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{1}$$\end{document}
. Here,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{1}$$\end{document}
![]() and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{2}$$\end{document}
and
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{2}$$\end{document}
![]() are exogenous measures of product preference and price.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {dW}$$\end{document}
are exogenous measures of product preference and price.
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {dW}$$\end{document}
![]() is Gaussian noise. The parameters of the model are the drift
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upphi }$$\end{document}
is Gaussian noise. The parameters of the model are the drift
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upphi }$$\end{document}
![]() (for the second alternative the drift is -
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upphi )}$$\end{document}
(for the second alternative the drift is -
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upphi )}$$\end{document}
![]() , the bias toward the fixated option
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upbeta }\in (0,1)$$\end{document}
, the bias toward the fixated option
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upbeta }\in (0,1)$$\end{document}
![]() , and error standard deviation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upupsilon }$$\end{document}
, and error standard deviation
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upupsilon }$$\end{document}
![]() .
.
5.4. Economic Models of Search and Choice
The model by Yang et al. (Reference Yang, Toubia and de Jong2015) is based on the assumption that consumer’s uncertainty about the true value of an attribute level
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l}$$\end{document}
![]() of a product,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {Z}_{\mathrm {j,m}}$$\end{document}
of a product,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {Z}_{\mathrm {j,m}}$$\end{document}
![]() (with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l}= 1,.., {\mathrm {L}_{\mathrm {m}}})$$\end{document}
(with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l}= 1,.., {\mathrm {L}_{\mathrm {m}}})$$\end{document}
![]() is reduced by extracting an (unknown) amount
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upeta }$$\end{document}
is reduced by extracting an (unknown) amount
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upeta }$$\end{document}
![]() of unbiased information through an eye fixation. Assuming a uniform distribution of prior beliefs across attribute levels, the posterior probabilities that attribute m of alternative j equals
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l}$$\end{document}
of unbiased information through an eye fixation. Assuming a uniform distribution of prior beliefs across attribute levels, the posterior probabilities that attribute m of alternative j equals
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l}$$\end{document}
![]() (with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l\, }= 1,.., {\mathrm {L}_{\mathrm {m}}})$$\end{document}
(with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {l\, }= 1,.., {\mathrm {L}_{\mathrm {m}}})$$\end{document}
![]() , given that person i has made
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}_{\mathrm {ijm}}$$\end{document}
, given that person i has made
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}_{\mathrm {ijm}}$$\end{document}
![]() fixations on it, are:
fixations on it, are:

The expected choice utility,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {U}_{\mathrm {ij(c)}},$$\end{document}
![]() which is accrued if product j is chosen, is modeled as a probability weighted sum of the part-utilities (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }_{\mathrm {i,m,l}})$$\end{document}
which is accrued if product j is chosen, is modeled as a probability weighted sum of the part-utilities (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upmu }_{\mathrm {i,m,l}})$$\end{document}
![]() of the attribute levels:
of the attribute levels:

The utility of search,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {U}_{\mathrm {i(s)}}$$\end{document}
![]() , is specified as a linear function of the saccade length and of horizontal and vertical tendencies. Consumers face the following maximization problem:
, is specified as a linear function of the saccade length and of horizontal and vertical tendencies. Consumers face the following maximization problem:

Equation (A.7) specifies a person i’s next action q as a choice between a) stopping search and choosing option j, which results in choice utility
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\mathop {\text{ max }}\limits _{\mathrm {q=j}}} {\mathrm {U}_{\mathrm {ij(c)}}\left( \mathrm {N}_{\mathrm {ij}}\mathrm {,\eta ,}{\upmu }_{\mathrm {i,m}} \right) }$$\end{document}
![]() , and b) continuing search and fixating the next attribute m of alternative j, which maximizes search utility
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {U}_{\mathrm {i}\left( \mathrm {s} \right) }$$\end{document}
, and b) continuing search and fixating the next attribute m of alternative j, which maximizes search utility
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {U}_{\mathrm {i}\left( \mathrm {s} \right) }$$\end{document}
![]() plus the expected maximum utility if the individual would stop after this next fixation, which equals
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum \nolimits _{\mathrm {l=1}}^{\mathrm {L}_{\mathrm {m}}} {\mathrm {p}\left( \mathrm {Z}_{\mathrm {j,m}}\mathrm {=l} \right) } {\mathop {\text{ max }}\limits _{\mathrm {j}}} {\mathrm {U}_{\mathrm {ij(c)}}\left( \mathrm {N}_{\mathrm {ij}}^{{*}}\mathrm {,\eta ,}{\upmu }_{\mathrm {I,m}} \right) }$$\end{document}
plus the expected maximum utility if the individual would stop after this next fixation, which equals
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\sum \nolimits _{\mathrm {l=1}}^{\mathrm {L}_{\mathrm {m}}} {\mathrm {p}\left( \mathrm {Z}_{\mathrm {j,m}}\mathrm {=l} \right) } {\mathop {\text{ max }}\limits _{\mathrm {j}}} {\mathrm {U}_{\mathrm {ij(c)}}\left( \mathrm {N}_{\mathrm {ij}}^{{*}}\mathrm {,\eta ,}{\upmu }_{\mathrm {I,m}} \right) }$$\end{document}
![]() , where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}_{\mathrm {ij}}^{{*}}$$\end{document}
, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}_{\mathrm {ij}}^{{*}}$$\end{document}
![]() is the vector with the number of fixations on option j.
is the vector with the number of fixations on option j.
Zhang, Ursu and Erdem (Reference Zhang, Ursu and Erdem2020) assume consumer i’s prior belief about brand j’s value is
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}\left( {\upalpha }_{\mathrm {ij,0}}, {\upsigma }_{\mathrm {ij,0}}^{\mathrm {2}} \right) $$\end{document}
![]() . The prior is updated with a noisy signal,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upeta }_{\mathrm {ijm,t}}{\sim N}\left( {\upmu }_{\mathrm {ijm}}, {\upomega }_{\mathrm {ijm}}^{\mathrm {2}} \right) $$\end{document}
. The prior is updated with a noisy signal,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upeta }_{\mathrm {ijm,t}}{\sim N}\left( {\upmu }_{\mathrm {ijm}}, {\upomega }_{\mathrm {ijm}}^{\mathrm {2}} \right) $$\end{document}
![]() from an eye fixation on attribute m and brand j at time t, resulting in brand value
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}\left( {\upalpha }_{\mathrm {ij,t}}, {\upsigma }_{\mathrm {ij,t}}^{\mathrm {2}} \right) $$\end{document}
from an eye fixation on attribute m and brand j at time t, resulting in brand value
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}\left( {\upalpha }_{\mathrm {ij,t}}, {\upsigma }_{\mathrm {ij,t}}^{\mathrm {2}} \right) $$\end{document}
![]() , with:
, with:

The prior mean
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upalpha }_{\mathrm {ij,0}}$$\end{document}
![]() is a linear function of brand ownership, the prior variance
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upsigma }_{\mathrm {ij,0}}^{\mathrm {2}}$$\end{document}
is a linear function of brand ownership, the prior variance
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upsigma }_{\mathrm {ij,0}}^{\mathrm {2}}$$\end{document}
![]() is a function of brand familiarity, and the variance of the signal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upomega }_{\mathrm {ijm}}^{\mathrm {2}}$$\end{document}
is a function of brand familiarity, and the variance of the signal
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upomega }_{\mathrm {ijm}}^{\mathrm {2}}$$\end{document}
![]() is a function of experience with attribute m. The expected choice utility of a brand equals:
is a function of experience with attribute m. The expected choice utility of a brand equals:
reflecting risk aversion with a risk coefficient r, by which a higher posterior uncertainty about a brand,
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upsigma }_{\mathrm {ij,t}}^{\mathrm {2}}$$\end{document}
![]() , decreases its utility. The inclusion of uncertainty as a function of risk aversion in equation (A.9) prioritizes eye-movements toward attributes that have received limited attention. Furthermore, like Yang et al. (Reference Yang, Toubia and de Jong2015), consumers are assumed to be one-step ahead forward looking, such that the utility derived from searching attribute m of product j is the maximum utility derived from choosing one of the alternatives at time t
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$+$$\end{document}
, decreases its utility. The inclusion of uncertainty as a function of risk aversion in equation (A.9) prioritizes eye-movements toward attributes that have received limited attention. Furthermore, like Yang et al. (Reference Yang, Toubia and de Jong2015), consumers are assumed to be one-step ahead forward looking, such that the utility derived from searching attribute m of product j is the maximum utility derived from choosing one of the alternatives at time t
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$+$$\end{document}
![]() 1:
1:
Equation (A.10) provides the expected value of choosing j at t
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$+$$\end{document}
![]() 1 after an additional search of j (the first term) minus the search costs
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {c}_{\mathrm {ij}}$$\end{document}
1 after an additional search of j (the first term) minus the search costs
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {c}_{\mathrm {ij}}$$\end{document}
![]() , or choosing any other option k at time t (the second term) minus the search costs. The latter are parameterized as a function of the vertical and horizontal saccade length, and fixations on white space.
, or choosing any other option k at time t (the second term) minus the search costs. The latter are parameterized as a function of the vertical and horizontal saccade length, and fixations on white space.
5.5. Satisficing Model of Search and Choice
Stüttgen et al. (Reference Stüttgen, Boatwright and Monroe2012) extend the model by van der Lans et al. (Reference van der Lans, Pieters and Wedel2008a) to a three-state HMM of satisficing choice, where
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t}}$$\end{document}
![]() indicates the state of individual i at fixation t. The model assumes that a consumer assigns the status satisfactory (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {S}_{\mathrm {ij,t}})$$\end{document}
indicates the state of individual i at fixation t. The model assumes that a consumer assigns the status satisfactory (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {S}_{\mathrm {ij,t}})$$\end{document}
![]() , unsatisfactory (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {U}_{\mathrm {ij,t}})$$\end{document}
, unsatisfactory (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {U}_{\mathrm {ij,t}})$$\end{document}
![]() , or undetermined (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{\mathrm {ij,t}})$$\end{document}
, or undetermined (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {D}_{\mathrm {ij,t}})$$\end{document}
![]() to each product at fixation t. If a product has not been fixated, its status is undetermined. To determine whether a product is satisfactory, a consumer needs to fixate all attributes m of that product and the value of each attribute needs to be acceptable, captured by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppsi }_{\mathrm {im}}{\in }\left\{ 0,1 \right\} {,\,}$$\end{document}
to each product at fixation t. If a product has not been fixated, its status is undetermined. To determine whether a product is satisfactory, a consumer needs to fixate all attributes m of that product and the value of each attribute needs to be acceptable, captured by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uppsi }_{\mathrm {im}}{\in }\left\{ 0,1 \right\} {,\,}$$\end{document}
![]() which follows a Bernoulli distribution. Thus:
which follows a Bernoulli distribution. Thus:

The first two states (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t}}{\in }\left\{ g,l \right\} )$$\end{document}
![]() in the HMM reflect the search process. In the global state (g), the decisions to fixate an ROI h follow a multinomial logit model with probabilities that are functions of the current status
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left\{ \mathrm {S}_{\mathrm {ij,t}}{\mathrm {,U}}_{\mathrm {ij,t}} \right\} $$\end{document}
in the HMM reflect the search process. In the global state (g), the decisions to fixate an ROI h follow a multinomial logit model with probabilities that are functions of the current status
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\left\{ \mathrm {S}_{\mathrm {ij,t}}{\mathrm {,U}}_{\mathrm {ij,t}} \right\} $$\end{document}
![]() of all products j and the size of ROI h. In the local state (l), the probabilities of fixating an ROI h are a function of the previously fixated ROI and of the ROIs bordering on it (reflecting local and re-fixations) captured via a vector of indicators
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {L}_{\mathrm {t}}\mathrm {(h)}$$\end{document}
of all products j and the size of ROI h. In the local state (l), the probabilities of fixating an ROI h are a function of the previously fixated ROI and of the ROIs bordering on it (reflecting local and re-fixations) captured via a vector of indicators
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {L}_{\mathrm {t}}\mathrm {(h)}$$\end{document}
![]() , in addition to a by-attribute strategy, captured via a vector of indicators
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {S}_{\mathrm {t}}\mathrm {(h)}$$\end{document}
, in addition to a by-attribute strategy, captured via a vector of indicators
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {S}_{\mathrm {t}}\mathrm {(h)}$$\end{document}
![]() . The fixation probabilities in the local (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upvarphi }_{\mathrm {l,t}}\mathrm {)}$$\end{document}
. The fixation probabilities in the local (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upvarphi }_{\mathrm {l,t}}\mathrm {)}$$\end{document}
![]() and global states (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upvarphi }_{\mathrm {g,t}}\mathrm {)}$$\end{document}
and global states (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upvarphi }_{\mathrm {g,t}}\mathrm {)}$$\end{document}
![]() , with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upbeta }_{\mathrm {i,\cdot ,\cdot }}$$\end{document}
, with
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\upbeta }_{\mathrm {i,\cdot ,\cdot }}$$\end{document}
![]() individual-level parameters to be estimated, are:
individual-level parameters to be estimated, are:
In the termination state (
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {w})$$\end{document}
![]() , the consumer chooses a product j that is satisfactory. Because the majority of participants continued searching after fully evaluating their final choice (which violates pure satisficing), the model assumes a verification stage to capture this. Therefore, it is possible that multiple products are satisfactory, leading to choice probabilities of satisfactory products that are equal to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {p}\left( {\mathrm {y}_{\mathrm {ij}}\mathrm {=1}}\vert {\mathrm {S}_{\mathrm {ij,T}}\mathrm {=1}}\right) =1 / S$$\end{document}
, the consumer chooses a product j that is satisfactory. Because the majority of participants continued searching after fully evaluating their final choice (which violates pure satisficing), the model assumes a verification stage to capture this. Therefore, it is possible that multiple products are satisfactory, leading to choice probabilities of satisfactory products that are equal to
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {p}\left( {\mathrm {y}_{\mathrm {ij}}\mathrm {=1}}\vert {\mathrm {S}_{\mathrm {ij,T}}\mathrm {=1}}\right) =1 / S$$\end{document}
![]() , while unsatisfactory products have a choice probability that equals zero:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {p}\left( {\mathrm {y}_{\mathrm {ij}}\mathrm {=1}}\vert {\mathrm {U}_{\mathrm {ij,T}}\mathrm {=1}}\right) \mathrm {=0,}$$\end{document}
, while unsatisfactory products have a choice probability that equals zero:
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {p}\left( {\mathrm {y}_{\mathrm {ij}}\mathrm {=1}}\vert {\mathrm {U}_{\mathrm {ij,T}}\mathrm {=1}}\right) \mathrm {=0,}$$\end{document}
![]() with S a normalizing constant. Finally, at odds with the theory of satisficing, some participants selected undetermined products, which was accommodated by a probability close to zero
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {p}\left( \mathrm {y}_{\mathrm {ij}} =1\big | \mathrm {D}_{\mathrm {ij,T}}=1\right) {\propto }{\epsilon } / \mathcal {S}with ({\epsilon }\sim Beta)$$\end{document}
with S a normalizing constant. Finally, at odds with the theory of satisficing, some participants selected undetermined products, which was accommodated by a probability close to zero
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {p}\left( \mathrm {y}_{\mathrm {ij}} =1\big | \mathrm {D}_{\mathrm {ij,T}}=1\right) {\propto }{\epsilon } / \mathcal {S}with ({\epsilon }\sim Beta)$$\end{document}
![]() . Switching probabilities between the three states represented by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t}}$$\end{document}
. Switching probabilities between the three states represented by
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t}}$$\end{document}
![]() are proportional to:
are proportional to:
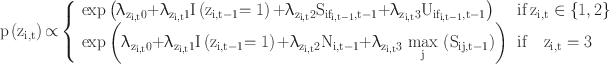
In equation (A.14),
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$${\uplambda }_{\mathrm {z}_{\mathrm {i,t}}\mathrm {0}}$$\end{document}
![]() captures the baseline switching probability to state
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t}}\mathrm {.} \quad {\uplambda }_{\mathrm {z}_{\mathrm {i,t}}\mathrm {1}}$$\end{document}
captures the baseline switching probability to state
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t}}\mathrm {.} \quad {\uplambda }_{\mathrm {z}_{\mathrm {i,t}}\mathrm {1}}$$\end{document}
![]() captures the dependence of that switching probability on the previous state
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t-1}}$$\end{document}
captures the dependence of that switching probability on the previous state
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {z}_{\mathrm {i,t-1}}$$\end{document}
![]() . Further, switching to the global and local states depends on whether the previously fixated product
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {f}_{\mathrm {i,t-1}}$$\end{document}
. Further, switching to the global and local states depends on whether the previously fixated product
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {f}_{\mathrm {i,t-1}}$$\end{document}
![]() is satisfactory or unsatisfactory, while switching to the termination states depends on the number of fixations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}_{\mathrm {i,t-1}}$$\end{document}
is satisfactory or unsatisfactory, while switching to the termination states depends on the number of fixations
\documentclass[12pt]{minimal}
\usepackage{amsmath}
\usepackage{wasysym}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{amsbsy}
\usepackage{mathrsfs}
\usepackage{upgreek}
\setlength{\oddsidemargin}{-69pt}
\begin{document}$$\mathrm {N}_{\mathrm {i,t-1}}$$\end{document}
![]() , and whether any of the choice alternatives is currently determined satisfactory.
, and whether any of the choice alternatives is currently determined satisfactory.





