Absolute Parameters of Detached Binaries in the Southern Sky – I: V349 Ara and V4403 Sgr

Abstract

We present the first analysis of spectroscopic and photometric observations of the two southern eclipsing binary stars, V349 Ara and V4403 Sgr. Radial velocity curves of these two systems obtained at the South African Astronomical Observatory and their V light curves from the All Sky Automated Survey were solved simultaneously using the Wilson–Devinney code. Our photometric models describe these two systems as Algol-like binary stars with detached configurations. The masses and radii were found to be 2.59 ± 0.07 M_⊙, 3.60 ± 0.07 R_⊙ and 2.51 ± 0.06 M_⊙, 4.15 ± 0.07 R_⊙ for the primary and secondary components of V349 Ara, respectively. Those of V4403 Sgr were derived to be 1.33 ± 0.02 M_⊙, 1.74 ± 0.02 R_⊙ and 1.59 ± 0.03 M_⊙, 2.50 ± 0.03 R_⊙ for the primary and secondary components, respectively. The distances to V349 Ara and V4403 Sgr were computed to be 677 ± 36 and 199 ± 10 pc from the dynamic parallax, respectively, taking into account interstellar extinction. The evolution cases of these two systems are also examined. Both components of these two systems are evolved main-sequence stars, and the dynamic ages were estimated as approximately 0.67 and 2.29 Gyr for V349 Ara and V4403 Sgr, respectively, when compared to Geneva theoretical evolution models.

1 INTRODUCTION

A variety of serious questions concerning stellar structure and evolution remain to be answered and require precise and detailed information on the physical parameters associated with actual stars (e.g. Christensen-Dalsgaard 2010; Christensen-Dalsgaard and Houdek 2010). Eclipsing binary (EB) systems offer one of the best-known routes to obtain precise values of these physical parameters. Since a large proportion of stars are in multiple systems, the knowledge gained from EB studies is vital to understanding the evolution of real populations in the Galaxy as a whole. It has been known for more than five decades that the structure and evolution of a star is determined by its mass and original chemical composition – and modified by processes like mass loss and mass transfer. By far, the most precise method to determine masses of real stars is through observations of EBs. Current observational techniques are capable of producing masses to a precision of 1–2% (Pavlovski and Southworth 2012), good enough to provide a stringent test of theoretical stellar evolutionary models. Yet, the actual number of systems analysed to this level of precision remains very small. As an example, in an exhaustive survey, Torres, Andersen, & Giménez (2010) could only identify a total of 95 detached EBs for which a precision of better than 3% had been obtained in the components mass values.

In order to increase the number of systems with reliable physical parameters that can be used to test evolutionary models, the authors of this paper embarked on a programme of obtaining detailed radial velocity (RV) measurements of southern detached EB systems which have not previously been studied for RVs and appear to have spectroscopically separable components. This paper reports the results obtained for two of these systems.

V349 Ara (BV 480 = HD 149573 = TYC 9038-641-1 = 2MASS J16392262-6057420, V=8.58 mag) was discovered by Strohmeier, Knigge, & Ott (1964) as a variable star. Using Bamberg photographic plates, they determined its photographic amplitude to be 0.4 mag. Schoeffel and Kohler (1965) published the first photometric light curve of V349 Ara and estimated its photometric period as 1.13837 d. However, Dvorak (2004) corrected this period of the system to 2.6518 d. Pojmanski and Maciejewski (2004a) also gave a period of 2.65178 d in a catalogue of ASAS (All Sky Automated Survey) data. Since then, unfortunately, it has been neglected. No detailed photometric and/or spectroscopic study has been made of V349 Ara. Only some estimated geometric and physical parameters of the system were given in the catalogues of Brancewicz and Dvorak (1980) and Malkov et al. (2006).

The eclipsing nature of V4403 Sgr (GSC 07415-04484 = HIP 91718 = 2MASS J18421146-3402250, V=8.62 mag) was revealed in HIPPARCOS observations (ESA 1997). The system was classified by Kazarovets et al. (1999) as a β Lyrae-type binary star. V4403 Sgr has a spectral type of F3V and amplitude of 0.32 mag ranging from 8.68 to 9.00 mag in the Hp band (ESA 1997). Pojmanski and Maciejewski (2004b) gave a period of 1.7014 d in ASAS data. V4403 Sgr was neglected after ASAS observations. No detailed photometric and/or spectroscopic studies of the system have so far been included in the literature. Only some estimated physical and geometrical parameters of the system were given in the EB catalogue of Malkov et al. (2006).

2 SPECTROSCOPIC OBSERVATIONS AND DATA REDUCTION

Spectroscopic observations of V349 Ara and V4403 Sgr were made at the Sutherland station of the South African Astronomical Observatory (SAAO), situated at an altitude of 1792 m, during three observing runs: 2012 July 4–10, 2013 July 24–31, and 2013 August 1–6. The grating spectrograph with SITe CCD camera installed at the Cassegrain focus of the 1.9-m telescope was used. The SITe CCD is effectively 266 × 1798 pixels in size, and is usable over wavelengths ranging from 0.35 μm. Its pixel size is 15 μm. Grating 4 of the spectrograph, which has a wavelength coverage of 410–510 nm with the blaze peak at 460 nm, a resolution of 0.1 nm (giving R = 4600 for the chosen wavelength range) and a slit width of 1.5 arcsec, was chosen for all the observations.

A total of 41 spectra for V349 Ara and 46 spectra for V4403 Sgr were obtained during the observations. Comparison spectra of a Cu/Ar arc lamp were taken before and after each stellar image. A set of Quartz–Iodine lamp images was also taken for flat-field calibrations. The standard star HD 693 (F8V, V_r = 14.81 km s⁻¹) was observed for the RV measurements of the components of V349 Ara and V4403 Sgr. The exposure time during all observations was 20 min. Data reduction and calibrations were carried out using the standard IRAF procedures.

3 MODELLING OF RADIAL VELOCITIES

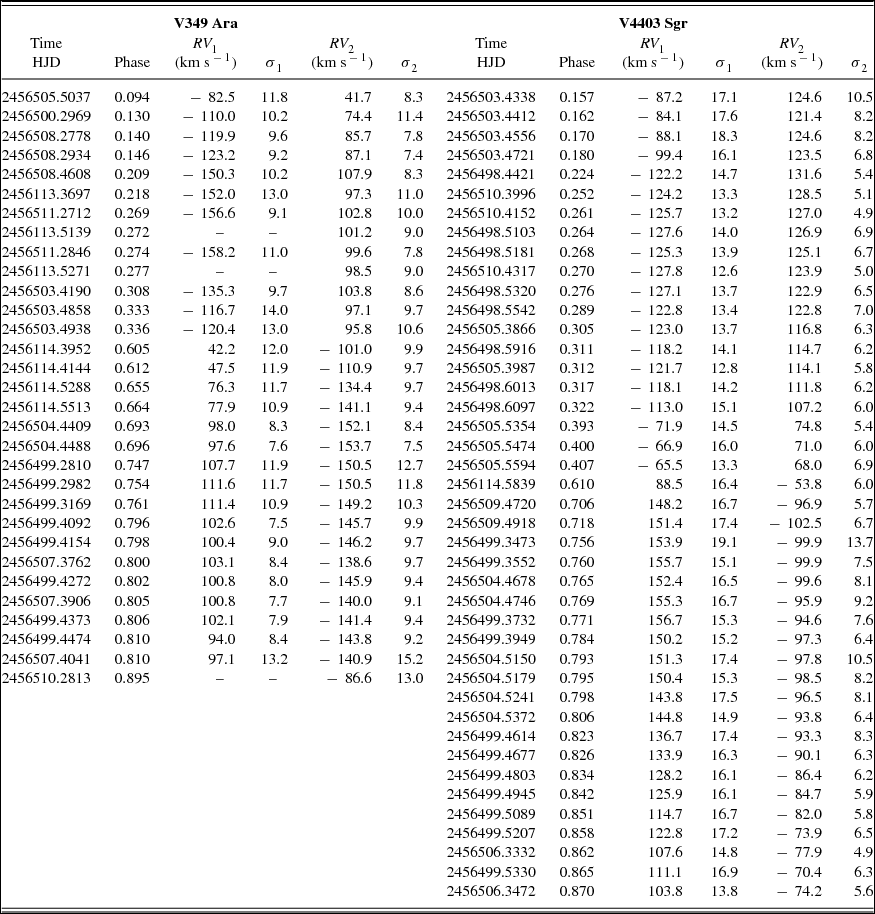
Measurements of RVs of the components of both EBs (V349 Ara and V4403 Sgr) were done by the cross-correlation technique (CCT). The FXCOR task in the RV package of iraf (Tonry and Davis 1979; Popper and Jeong 1994) was used for the cross-correlation. The Hβ (4861.33 Å) lines of the components of V349 Ara and V4403 Sgr were chosen as the most suitable lines for reliable RV measurements. In this process, the Gaussian function was adopted as the best-fitting one, and the spectra of HD693 were used as a template for deriving RVs of components of these two systems. The RV measurements, with standard errors, of components of V349 Ara and V4403 Sgr are given in Table 1. In this table, phase values of observed time of RVs were calculated using the linear ephemeris given in Table 2.

Table 1. RV measurements, with standard errors, of components of V349 Ara and V4403 Sgr.

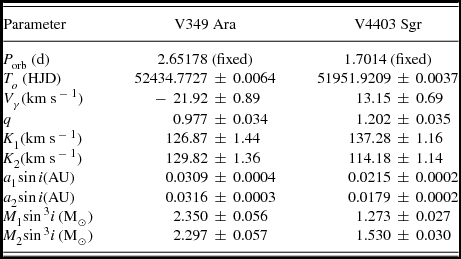
Table 2. Spectroscopic orbital parameters of V349 Ara and V4403 Sgr.

In order to obtain orbital parameters from the RV data derived from the CCT, the ELEMDR77 program, developed by T. Pribulla (private communication), was used. After several iterations, the ELEMDR77 program gave a value close to zero for the eccentricity, e, within its uncertainties, for both systems. For this reason, we assumed a circular orbit for each of the two binary systems. Additionally, during the fitting, the orbital periods P _orb of V349 Ara and V4403 Sgr were fixed to be 1.7014 and 2.65178 d (from Pojmanski and Maciejewski 2004a, Pojmanski and Maciejewski 2004b), respectively. The velocity semi-amplitudes K ₁ and K ₂ of the components and the conjunction time T ₀ were the adjusted parameters. The best-fitting orbital elements for V349 Ara and V4403 Sgr are given in Table 2.

4 SIMULTANEOUS SOLUTION OF THE LIGHT AND RADIAL VELOCITY CURVES

To obtain absolute parameters of these two southern EBs (V349 Ara and V4403 Sgr), we solved ASAS V light curves (Pojmanski and Maciejewski 2004a, Pojmanski and Maciejewski 2004b) and our RV curves of them, using the Wilson–Devinney (W–D) method (Wilson and Devinney 1971, version 1996).

During analysis, the adopted parameters were as follows. We used the values of masses of primary components of these two systems derived from our RV curves solution (see Section 3) to estimate their effective temperatures. We then adopted 9074 and 6517 K for the effective temperatures of primary components of V349 Ara and V4403 Sgr, respectively, according to Cox (2000) mass–temperature calibration. A square-root limb-darkening law was adopted and limb-darkening coefficients were taken from Claret and Bloemen (2011) and Claret, Hauschildt, & Witte (2013) according to the filter wavelengths used and effective temperatures of the components. The bolometric gravity-darkening exponents of the components were taken to be 1.0 for a radiative atmosphere (T > 7200 K) from von Zeipel (1924) and 0.32 for a convective atmosphere (T < 7200 K) from Lucy (1967). Also, the bolometric albedos of the components were fixed to 1.0 and 0.5 for radiative and convective atmospheres, respectively, following Rucinski (1969). Synchronous rotation of the components was assumed. A circular orbit for the systems was adopted from the spectroscopic orbital solution described in Section 3. These parameters were kept constant during all iterations.

The adjusted parameters in the iterations of the W–D program were the semi-major axis of orbit (A), phase shift (ϕ), systemic velocity of binary (V _γ), orbital inclination (i), surface temperature of secondary component (T ₂), mass ratio (q = M ₂/M ₁), non-dimensional surface potentials of both components Ω₁ and Ω₂, and fractional monochromatic luminosity of the primary component (L ₁/L _total). The initial values of q, A, and V _γ were taken from the RV solutions (Section 3). A third light contribution was also considered as an adjustable parameter in order to check the probability of a third component. However, since the resulting third light contribution was too small (i.e., negligible) and within the standard deviations, this was excluded from the list of adjustable parameters. The iterations were made in MODE 2, which corresponds to the detached configuration.

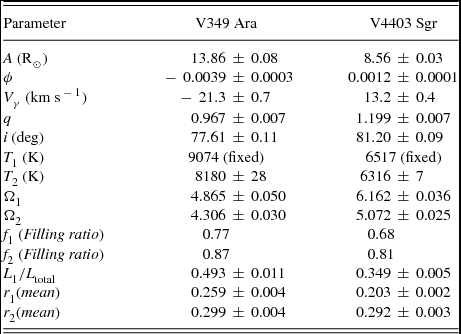
The final models for these two southern binary stars are given in Table 3. Comparisons between observed and computed light and RV curves are shown in Figures 1 and 2.

Table 3. Final solutions of ASAS V light and RV curves of V349 Ara and V4403 Sgr.

Figure 1. (a) Best W–D fits to the ASAS V light curve of V349 Ara. (b) Best W–D fits to the radial velocity curves of components of V349 Ara.

Figure 2. (a) Best W–D fits to the ASAS V light curve of V4403 Sgr. (b) Best W–D fits to the radial velocity curves of components of V4403 Sgr.

5 RESULTS AND DISCUSSION

The SAAO grating spectra of V349 Ara and V4403 Sgr were analysed, and then RV curves of the components of these two southern EBs were obtained. First, orbital solutions of these two neglected binaries gave quite large spectroscopic mass ratios of 0.977 ± 0.034 and 1.202 ± 0.035 for V349 Ara and V4403 Sgr, respectively. The ASAS V light and SAAO RV curves of these two systems were simultaneously solved using the W–D code. Finally, photometric solutions describe these two systems as detached EB stars. The primary and secondary components fill 77 and 87% of their Roche lobes in the case of V349 Ara; and in the case of V4403 Sgr; 68 and 81%, respectively.

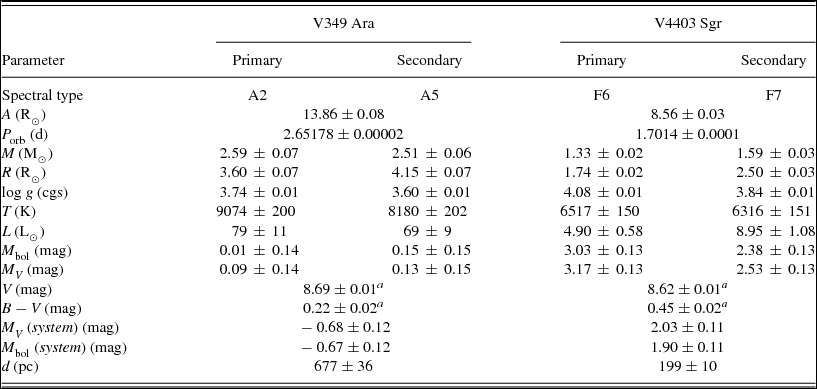
Simultaneous solutions of the ASAS V light and RV curves were used to calculate the absolute parameters of component stars of these two binaries. The resulting parameters are given in Table 4 with their standard errors. In the calculations, T _eff = 5771.8 ± 0.7 K, M _bol = 4.7554 ± 0.0004 mag, BC = − 0.107 ± 0.02 mag, and g=27423.2 ± 7.9 were used for solar values (Pecaut and Mamajek 2013). As mentioned in Section 4, according to the masses of primary components of these two detached systems, derived from the RV curves solution of the system (see Section 3) and calibration of MK spectral types given by Cox (2000), the spectral types and effective temperatures of primary components of V349 Ara and V4403 Sgr were determined as A2V, 9074 ± 200 K and F6V, 6517 ± 150 K, respectively. However, the spectral type of V349 Ara was given as A5V by Houk and Cowley (1975). On the other hand, according to the colour index of the system (B–V = 0.22 ± 0.02 mag derived from HIPPARCOS observation by reducing to the Johnson UBV system), the spectral type of the system could be estimated as A7V. For V4403 Sgr, the spectral type was given as F3V in SIMBAD database. However, the spectral type of the system could be assigned as F4V corresponding to the revised colour index of B–V = 0.42 ± 0.03 mag determined from HIPPARCOS observations, according to Cox (2000) colour index-spectral type calibration. The standard errors of the effective temperatures of secondary components, 28 and 7 K for V349 Ara and V4403 Sgr, given in Table 3, are the formal 1σ errors arising from the W–D light curve solution. The corrected standard errors of the effective temperatures of secondary components of V349 Ara and V4403 Sgr could be estimated as 202 and 151 K based on the standard errors of 200 and 150 K in the effective temperatures of their primary components, respectively.

Table 4. Absolute parameters of components of V349 Ara and V4403 Sgr.

^a ESA (1997).

Bolometric corrections for the components of these two systems were derived from the tabulation of Flower (1996), according to their effective temperatures. In determining the distances to these two binaries, the interstellar extinction in the V band was then computed as A _V = 3.1 × E(B − V). The distances to V4403 Sgr and V349 Ara—with corrections for interstellar absorption—were found to be 199 ± 10 and 677 ± 36 pc using the distance modulus. According to the revised HIPPARCOS parallax (van Leeuwen 2007), the distance to V4403 Sgr is 202 ± 41 pc. This consistency between the dynamic and HIPPARCOS parallax within standard errors shows the accuracy of the observationally determined absolute parameters of V4403 Sgr. On the other hand, unfortunately, there are no HIPPARCOS observations of V349 Ara to compare the photometric and dynamic parallax.

The Geneva evolutionary models (Ekström et al. 2012; Yusof et al. 2013) were chosen to compare the physical parameters of V349 Ara and V4403 Sgr with theoretical model predictions. The log (age)–radius diagrams were used to estimate the ages of these two detached systems. Then, the isochrones of determined ages were checked using the Hertzsprung–Russell (HR; log (T _eff)–log (L)) diagrams. Results are shown in Figures 3 and 4 for V349 Ara and V4403 Sgr, respectively, given a solar metallicity of Z = 0.014 (Asplund et al. 2009).

Figure 3. Comparison between physical parameters of V349 Ara and predictions of Geneva stellar evolutionary models in (a) log (age)–radius diagram, (b) log (T _eff)–log (L) diagram. Filled and open circle symbols represent hotter and cooler components, respectively. Vertical and horizontal lines show error bars of the measured quantities. Red solid line is the isochrone for log(age) = 8.823 in HR diagram. Zero-age main-sequence (ZAMS), terminal-age main-sequence (TAMS), the evolutionary tracks and isochrones were taken from Geneva models for the solar chemical composition. The numbers in HR diagram denote initial masses.

Figure 4. Comparison between physical parameters of V4403 Sgr and predictions of Geneva stellar evolutionary models in (a) log (age)–radius diagram, (b) log (T _eff)–log (L) diagram. Filled and open circle symbols represent hotter and cooler components, respectively. Vertical and horizontal lines show error bars of the measured quantities. Red-dashed line is isochrone for log(age)=9.36 in HR diagram. Zero-age main-sequence (ZAMS), terminal-age main-sequence (TAMS), the evolutionary tracks and isochrones were taken from Geneva models for the solar chemical composition. The numbers in HR diagram denote initial masses.

Figure 3(a) shows the growth of mean radii of the components of V349 Ara with age for its measured masses (black solid and dashed lines for the primary and secondary component masses of 2.59and 2.51 M_⊙, respectively). According to these Geneva evolutionary models, the measured radius of the primary component is not reached until 0.55 Gyr, while the secondary component has attained the measured radius by 0.63 and 0.67 Gyr. Given the present filling ratio of 0.87 of the secondary component, it is possible that the secondary component exceeded its Roche limit sometime in the past and was therefore initially more massive than now, which would mean that it is actually younger than it appears according to the model fitting. Likewise, that would mean that the primary component gained transferring mass from the secondary component in the past, and it is actually older than it appears based on the model fitting. That could bring the ages into line at a point midway between 0.55 and 0.67 Gyr. Another reason for this difference between the two ages might be that the more massive and hotter primary component (3.60 R_⊙) is smaller than the less massive and cooler secondary component (4.15 R_⊙). Usually, the more massive component in a (non-compact) binary system is also the larger one. However, the age discrepancy appears to be resolved in the HR diagram in Figure 3(b), where a single isochrone fits both components within the errors. The smaller and hotter primary component of V349 Ara is still on the main sequence, approaching the terminal age main sequence (TAMS), while the larger and cooler secondary component has evolved slightly beyond the TAMS.

We see the same behaviour in Figure 4(a), where the growth of the mean radii of the components of V4403 Sgr is displayed (black solid and dashed lines for the primary and secondary component masses of 1.33 and 1.59 M_⊙, respectively). The measured radius of the primary component is attained at 3.31 Gyr, while the secondary component takes 2.19 Gyr. As argued for V349 Ara, this discrepancy could be the result of a mass transfer episode, although less likely in V4403 Sgr than in V349 Ara, given the smaller filling ratio for the secondary component of V4403 Sgr. Again, another reason for this difference between the two ages might be that the primary component (1.33 M_⊙) is less massive than the secondary component (1.59 M_⊙). Usually, the primary component in an EB system is the more massive one. On the other hand, according to the HR diagram in Figure 4(b), the isochrone for the best-fitting age of 2.29 Gyr provide an excellent match to the masses, effective temperatures, and luminosities of V4403 Sgr. The less massive and hotter primary component is still on the main sequence, while the more massive and cooler secondary component is very close to the turn-off point from the main sequence.

Other sets of model predictions (e.g. Bressan et al. 2012) were investigated and similar results were found. Finally, in view of the various uncertainties, the mean ages of the systems are estimated from the theoretical isochrones as 0.67 Gyr and 2.29 Gyr for V349 Ara and V4403 Sgr, respectively.