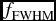Black Hole Mass Estimation: How Good is the Virial Estimate?

Abstract

Black hole mass is a key factor in determining how a black hole interacts with its environment. However, the determination of black hole masses at high redshifts depends on secondary mass estimators, which are based on empirical relationships and broad approximations. A dynamical disk wind broad line region model (BLR) of active galactic nuclei is built in order to test the impact of different BLR geometries and inclination angles on the black hole mass estimation. Monte Carlo simulations of two disk wind models are constructed to recover the virial scale factor, f, at various inclination angles. The resulting f values strongly correlate with inclination angle, with large f values associated with small inclination angles (close to face-on) and small f values with large inclination angles (close to edge-on). The recovered f factors are consistent with previously determined f values, found from empirical relationships. Setting f as a constant may introduce a bias into virial black hole mass estimates for a large sample of active galactic nuclei. However, the extent of the bias depends on the line width characterisation (e.g. full width at half maximum or line dispersion). Masses estimated using $f_{\text{FWHM}}$ tend to be biased towards larger masses, but this can generally be corrected by calibrating for the width or shape of the emission line.

1 INTRODUCTION

Black holes are widely believed to be located at the centre of most galaxies, both active and quiescent galaxies (Kormendy & Richstone 1995; Richstone 1998; Ferrarese & Ford 2005; Kormendy & Ho 2013). Relationships have long been observed between the mass of the black hole and the properties of the host-galaxy, namely stellar velocity dispersion (the $M_{\text{BH}} \text{--} \sigma _{*}$ relation; Ferrarese & Merritt 2000; Gültekin et al. 2009; McConnell & Ma 2013), light concentration (the $M_{\text{BH}} \text{--} C_{r_{c}}$ relation; Graham et al. 2001), bulge luminosity and bulge stellar mass (the $M_{\text{BH}} \text{--} L_{\text{bulge}}$ and $M_{\text{BH}} \text{--} M_{\text{bulge}}$ relations; Magorrian et al. 1998; Marconi & Hunt 2003; McConnell & Ma 2013). Despite this, the origin of these correlations and the role of the central black hole in galaxy evolution, are still not well understood (Silk & Rees 1998; King 2003, 2005; Di Matteo, Springel, & Hernquist 2005; Murray, Quataert, & Thompson 2005; Di Matteo et al. 2008; Park et al. 2015). The properties of a black hole can be related to its mass, M _BH, and to understand the interplay between the black hole and its host galaxy, we require precise and accurate M _BH measurements over a broad range of galaxy properties and cosmic time.

The value of M _BH can be measured directly using the dynamics of stars or gas in close proximity to the black hole (Ferrarese & Ford 2005; McConnell & Ma 2013). However, this method is limited to the local universe due to the high spatial resolution required. An alternative method of black hole mass estimation is reverberation mapping (RM; Blandford & McKee 1982; Peterson 1993) of active galactic nuclei (AGN). Variable continuum emission originating from the accretion disk is absorbed by nearby gas deep within the gravitational potential of the black hole (broad line region; BLR). The BLR gas reprocesses this radiation and emits Doppler broadened emission lines. The corresponding emission line flux is observed to vary in response to the continuum flux in a roughly linear fashion with a time delay, τ. This time delay corresponds to the light travel time to the mean responsivity weighted distance to the BLR from the accretion disk. RM is based on the assumption that there is a simple, though not necessarily linear, relationship between the observed continuum and the ionising continuum (Peterson 1993). In general, the emission line response has been found to be approximately linear in fashion; however, non-linear responses have been observed in NGC7469 (Peterson et al. 2014), NGC5548 (De Rosa et al. 2015) during the second half of the campaign, and J080131 (Du et al. 2015). The mechanism causing the observed non-linear response in these objects is not well understood.

Under the assumption that the gas in the BLR is virialised and its motion is dominated by the gravitational field of the central black hole, the mass of the black hole is (Peterson & Wandel 1999)

(1) $$\begin{equation} M_{\text{BH}}=f\left(\frac{\Delta V^{2}R}{G}\right)=fM_{\text{vir}}, \end{equation}$$

where R = cτ is the radius of the emitting line, c is the speed of light, and G is the gravitational constant. The velocity dispersion, denoted by ΔV, is determined from the width of an individual broad emission line by measuring the full width at half maximum (FWHM) or the line dispersion, σ_line, and f is the virial factor that links the line-of-sight virial product, $M_{\text{vir}}$ , to the true black hole mass.

RM has yielded masses for approximately 60 AGN (Bentz & Katz 2015) and the values of R have been found to exhibit a tight power law relationship with the AGN continuum luminosity, λL _λ (Kaspi et al. 2000; Bentz et al. 2009, 2013), as predicted from simple photoionisation physics (Davidson 1972; Krolik & McKee 1978). This strong correlation is the basis of single-epoch virial black hole mass estimators (‘virial BH mass estimators’ for short), which estimate the mass of the black hole using a single epoch of spectroscopy (e.g. Laor 1998; Wandel, Peterson, & Malkan 1999; McLure & Jarvis 2002; Vestergaard & Peterson 2006). The single epoch mass estimation method is routinely used to estimate black hole masses (e.g. Vestergaard et al. 2008; Vestergaard & Osmer 2009; Willott et al. 2010; Schulze & Wisotzki 2010; Mortlock et al. 2011; Trump et al. 2011; Shen & Liu 2012; Kelly & Shen 2013), and allows the black hole–galaxy correlations to be studied using large samples of galaxies. Several different virial BH mass estimators have been developed in the last decade, based on different line width characterisations and different lines. However, the FWHM of the Hβ, Mg ii, and C iv emission lines and a set value of f, are commonly used. Due to the widespread use of virial BH mass estimators, it is critical to fully understand the variation expected in f within the AGN population.

The value of the f factor depends on the structure, kinematics, dynamics, and orientation of the BLR with respect to the observer. Its value is expected to be different for every AGN. Nevertheless, it is a common practice to adopt a single f factor value for all AGNs, calibrated from the local RM sample under the assumption that the $M_{\text{BH}} \text{--} \sigma _{*}$ relation is consistent between quiescent and active galaxies (Gebhardt et al. 2000; Ferrarese et al. 2001). The value of f also depends on line width characterisation (e.g. FWHM or σ_line) and whether the mean or rms spectrum is used for the line width measurement. Recent measurements of ⟨f⟩ based on rms spectra and σ_line vary between ⟨f _σ⟩ = 2.8^+0.7 _−0.5 (Graham et al. 2011) and ⟨f _σ⟩ = 5.5 ± 1.8 (Onken et al. 2004), with most ⟨f _σ⟩ values lying within the range of $\langle f_{\sigma } \rangle \sim 4 \text{--} 6$ (Collin et al. 2006; Park et al. 2012; Grier 2013; Woo et al. 2013; Pancoast et al. 2014; Woo et al. 2015). The ⟨f _σ⟩ obtained from mean spectra is 3.85 ± 1.15 (Collin et al. 2006). On the other hand, the mean $f_{\text{FWHM}}$ measured using rms spectra were found to be $\langle f_{\text{FWHM}} \rangle =1.12^{+0.36}_{-0.27}$ by Woo et al. (2015) and $\langle f_{\text{FWHM}} \rangle =1.44 \pm 0.49$ by Collin et al. (2006). The $\langle f_{\text{FWHM}} \rangle$ using mean spectra is 1.17 ± 0.50 (Collin et al. 2006). The calibration of the f factor makes RM a secondary mass estimation method. The typical uncertainties in reverberation masses resulting from the uncertainty in f is ~ 0.43 dex (Woo et al. 2010), due to the intrinsic scatter in the $M_{\text{BH}} \text{--} \sigma _{*}$ relation.

Disk wind models provide a promising explanation for the observed broad absorption lines (BALs) and the blueshift of high-ionisation line relative to low-ionisation emission line, and are therefore the favoured model of the BLR (Murray et al. 1995, hereafter M95; Elvis 2004, hereafter E04). However, there is some evidence that the kinematics of low ionisation lines, such as Hβ, are dominated by simple virialised rotation models (Peterson & Wandel 1999; Kollatschny 2003; Kollatschny & Zetzl 2013). Thus, it is still an open question as to whether disk wind models apply to some or all emission lines. We attempt to recover a theoretical prediction of the f factor based on a dynamical disk wind model of the BLR and investigate the impact of orientation on the value of f.

The overview of the paper is as follows. In Section 2, we describe our approach in modelling the disk wind. The results of the simulations are presented in Section 3. In Section 4, we discuss our findings and compare them to previous studies. The conclusions are given in Section 5.

2 DISK WIND MODEL

Our BLR disk wind model is based on the cylindrical disk wind model introduced by Shlosman & Vitello (1993), originally used to model cataclysmic variable stars (CVs). The model consists of a flat, opaque, and geometrically thin accretion disk and a thick, conical BLR wind. A simplified sketch is shown in Figure 1. The similarities in the geometries, kinematics, and ionisation state between CVs and AGNs, suggest this model can be implemented to study the characteristics of AGN (Higginbottom et al. 2013, 2014).

Figure 1. A sketch of the key parameters used to describe the cylindrical disk wind model.

The properties of our cylindrical disk wind models are based on two well-known disk wind models, the M95 line-driven disk wind model and the E04 funnel disk wind model. The details of our model are given in the following sections.

2.1. Kinematics of the wind

AGN are assumed to have an axially rather than a spherically symmetric geometry. Therefore, it is preferable to describe the model using cylindrical coordinates (r, ϕ, z). The variables r and ϕ are the radial and azimuthal coordinates on the xy-plane, which is on the surface of the accretion disk. The rotation axis of the disk is aligned with the z axis. The inclination angle, i, is defined from the z axis to the observer’s line-of-sight.

The outflowing wind is launched from the accretion disk at radii between $r_{\text{min}}$ and $r_{\text{max}}$ along fixed streamlines. Each point in the wind spirals upwards in a three-dimensional helix with a fixed opening angle, θ. The opening angle of each stream line is situated within a minimum angle, $\theta _{\text{min}}$ , and maximum angle, $\theta _{\text{max}}$ , and its value depends on the origin position of the streamline from the accretion disk, such that

(2) $$\begin{equation} \theta =\theta _{\text{min}}+(\theta _{\text{max}}-\theta _{\text{min}})x^{\gamma }, \end{equation}$$

where $x=(r_{0}-r_{\text{min}})/(r_{\text{max}}-r_{\text{min}})$ , r ₀ is the origin position of a single streamline, and γ is used to adjust the concentration of the streamlines toward either the inner or outer boundaries of the wind. Throughout our investigations we have set γ = 1, which corresponds to even angular spacing between the streamlines.

The velocity components at any given position in the wind can be given in terms of the radial, rotational, and vertical velocity, v_r, v _ϕ, and v_z . Alternatively, the velocity can be expressed in terms of poloidal velocity, v_l , and rotational velocity, v _ϕ. The poloidal velocity or the velocity along the streamline is

(3) $$\begin{equation} v_{l}=v_{0}+(v_{\infty }-v_{0})\left[\frac{(l/R_{v})^{\alpha }}{(l/R_{v})^{\alpha }+1}\right], \end{equation}$$

where v ₀ is the initial poloidal wind velocity at the surface of the disk (set arbitrarily at 6 km s⁻¹; Higginbottom et al. 2013; Shlosman & Vitello 1993), l = [(r − r ₀)² + z ²]^1/2 is the distance along a poloidal streamline, R_v is the wind acceleration scale height characterising the scale at which the wind reaches half its terminal velocity v _∞, and α is a power-law index that controls the shape of the acceleration profile. We set α = 1, which implies a slow increase in acceleration along each poloidal streamline. Furthermore, v_l is correlated to v_r and v_z such that v_r = v_l sinθ and v_z = v_l cosθ. In our model, the asymptotic wind velocity or the terminal velocity, v _∞, is taken to be equal to the escape velocity, $v_{\text{esc}}=(2GM_{\text{BH}}/r_{0})^{1/2}$ .

At the base of the wind, the rotational velocity is assumed to follow Keplerian motion, $v_{\phi ,0}=(GM_{\text{BH}}/r_{0})^{1/2}$ . As the wind rises above the disk and expands, we assume the rotational velocity decreases linearly,

(4) $$\begin{equation} v_{\phi }=v_{\phi ,0}\left(\frac{r_{0}}{r}\right). \end{equation}$$

This conserves angular momentum about the rotation axis. For each position (r, z), the density of the wind, ρ, follows the continuity equation specified by

(5) $$\begin{equation} \rho (r,z)=\frac{r_{0}}{r}\frac{\mathop {}\!\mathrm{d}r_{0}}{\mathop {}\!\mathrm{d}r}\frac{\dot{m}(r_{0})}{v_{z}(r,z)}, \end{equation}$$

where the factor $(r_{0}/r)(\mathop {}\!\mathrm{d}r_{0}/\mathop {}\!\mathrm{d}r)$ scales as the streamline area increases with outflowing wind. The mass-loss rate per unit surface of the disk, $\dot{m}$ , is

(6) $$\begin{equation} \dot{m}(r_{0})=\dot{M}_{\text{wind}}\frac{r^{\lambda }_{0}\cos \theta (r_{0})}{\int \mathop {}\!\mathrm{d}A\,r^{\prime \lambda }_{0}\cos \theta (r^{\prime }_{0})}, \end{equation}$$

where $\dot{M}_{\text{wind}}$ is the total mass-loss rate of the wind, λ is the mass-loss rate exponential, and the term cosθ represents the angle formed between the streamline and the disk. A uniform mass-loss with radius is indicated by λ = 0. For a high luminosity source L ≈ 10⁴⁶ergs⁻¹ and black hole of mass $10^{8}\,\text{M}_{\odot }$ , the total mass accretion rate is $\dot{M}_{\text{acc}} \approx 2\,\text{M}_{\odot }\,$ yr⁻¹ with efficiency η = 0.1 (Peterson 1997). Here, $\dot{M}_{\text{wind}}$ is taken to be equivalent to $\dot{M}_{\text{acc}}$ .

The relevant parameter values chosen for the M95 and E04 disk wind models are shown in Table 1. The black hole mass was set to $10^{8}\,\text{M}_{\odot }$ with corresponding values of wind radius from M95 and E04. In both cases, the wind region is defined out to the radius of the BLR, $r_{\text{BLR}} \sim 10^{17}\,$ cm. The M95 and E04 models have different heights and are scaled accordingly by $r_{\text{BLR}}$ and the wind angle, $\theta _{\text{min}}$ and $\theta _{\text{max}}$ , as illustrated in Figure 2. The opening angle of the M95 model is close to the base of the accretion disk with a wider range of wind radii, and hence the height is shallow compared to the E04 model. To account for the possibility that ~ 20% of QSOs have BAL feature (Knigge et al. 2008), the wind opening angle is specified to be within 20° for both models. For simplicity, the vertical wind that is initially lifted off the disk in E04 model is omitted.

Figure 2. The numbered regions describe different ‘wind zones’ where emission lines might be generated for M95 (left, blue) and E04 (right, cyan) disk wind models.

Table 1. Adopted fiducial values of the parameters.

^a Chosen values to mimic Murray et al. (1995) model. ^b Chosen values to mimic Elvis (2004) model.

There is strong evidence that the gas in the BLR is stratified, with high ionisation lines situated closer to the ionising source than the low ionisation lines (Peterson & Wandel 1999; Kollatschny 2003; Peterson 2014). We divide our disk wind model into different ‘wind zones’ to account for the stratification of the wind in the BLR region. The wind is divided evenly into zones of three rows and four columns, as depicted in Figure 2. Each zone [a, b] is labelled according to its row and column position.

2.2. Line profile creation

Once the disk wind model is established, the expected emission line profile is computed using a Monte Carlo simulation. Initially, a large number of particles dictated by the density profile, are randomly generated in cylindrical coordinates (r, ϕ, z) within the confines of the allowed ‘wind zone’. The projected velocity along the line-of-sight, $v_{\text{los}}$ , is then evaluated for each particle as a function of inclination angle, i. From the calculated line-of-sight velocity, kernel density estimation (KDE) is performed to estimate the shape of the underlying line profile. Line profiles are created for individual zones for inclination angles between 5° and 85°. We assume that there is no obscuration or shielding due to the dusty torus. Photoionisation is not included in this model but will be incorporated in future work.

2.3. The f factor

For each ‘wind zone’ line profile, the FWHM and σ_line values are measured and the corresponding f factor is calculated using Equation (1). As Hβ is typically used to calculate the black hole mass in RM studies (Collin et al. 2006; Park et al. 2012; Grier 2013; Woo et al. 2013; Pancoast et al. 2014; Woo et al. 2015), we concentrate our analysis on a wind zone close to the base of the wind and towards the outer edge of the BLR, corresponding to expectations for Hβ emission. To make the two models approximately comparable in terms of radial scales, zone [2, 2] is chosen for both models. We also calculate the probability of measuring a given black hole mass based on a fixed f value from the literature using the cumulative probability of viewing a quasar at any given inclination angle, i, of F(i) = 1 − cos(i), with 0° ⩽ i ⩽ 90°.

The response of an individual emission line to changes in the continuum flux is expected to vary depending on where the line is emitted within the disk wind and the luminosity of the AGN (due to differences in density and ionising flux; Korista & Goad 2000, 2004). Without further assumptions about the degree of continuum variability and luminosity and further photoionisation modelling, it becomes impossible to model rms spectra. Therefore, we only compare our generated spectra with the f factors measured using the mean spectra.

3 RESULTS

The range of f factors found for the M95 and E04 disk wind models at various inclination angles and for various zones are presented in Table 2. The range of f factors found extend well beyond the spread prescribed in the empirically determined ⟨f⟩ values (Collin et al. 2006).

Table 2. Values of f for different zones.

^a Compare with $\langle f_{\text{FWHM(H$\beta $)}} \rangle =1.17 \pm 0.50$ (or $\log _{10}\langle f_{\text{FWHM(H$\beta $)}} \rangle =0.07^{+0.15}_{-0.24}$ ) from Collin et al. (2006). ^b Compare with $\langle f_{\sigma (\text{H}\beta )} \rangle =3.85 \pm 1.15$ (or $\log _{10}\langle f_{\sigma (\text{H}\beta )} \rangle =0.59^{+0.11}_{-0.15}$ ) from Collin et al. (2006).

The distribution of f factors with inclination angle for the equivalent Hβ wind zone, in both models, is shown in Figure 3. The agreement between the empirically determined f value from Collin et al. (2006) and our predictions varies between the two velocity dispersion characterisations. The Collin et al. (2006) $f_{\text{FWHM}}$ measurement coincided with middle range viewing angle (around 25° to 40°) predictions using our disk wind models. Meanwhile, the Collin et al. (2006) f _σ measurement was consistent with our prediction for a high inclination angle (edge-on) disk wind model.

Figure 3. Plot of f factors against inclination angle for Hβ line characterised by emission from the [2, 2] location in the wind zone for the M95 (blue) and E04 (cyan) disk wind models. Upper: Virial factor using FWHM, $f_{\text{FWHM}}$ . Lower: Virial factor using σ_line, f _σ. The dashed lines are the mean f factor, ⟨f⟩, with uncertainties (shaded) from Collin et al. (2006). The $f_{\text{FWHM(H$\beta $)}}$ for individual quasars from Pancoast et al. (2014) are shown by green circles with error bars in the upper panel.

Our predictions for f were found to cover a similar range of values as those found using direct modelling estimates of Pancoast et al. (2014). Pancoast et al. (2014) estimated the f factor via direct BLR modelling using RM data of five Seyfert galaxies. Our predicted $f_{\text{FWHM}}$ values also follow the general trend with inclination of the Pancoast et al. (2014) results; however, our results display a systematic shift towards larger f values.

The f value as a function of inclination angle for selected wind zones [0, 3], [2, 0], and [2, 3] is illustrated in Figure 4. The zones provide some indication of the f values for different emission lines expected to be emitted from different locations in the wind. The recovered values of f are generally consistent between all wind zones. The wind is dominated by virialised rotational dynamics for wind zones close to the base of the wind. For wind zones at large r and small z (e.g. [2, 3]), f has a steeper trend with inclination and its value is generally larger than the f factor obtained in wind zones closer to the ionisation source (e.g. [2, 0]). In the E04 model, the wind in zones [2, 1], [2, 2], and [2, 3] are located above the accretion disk (Figure 2, right). Since the initial positions of the streamlines, r ₀, are contained within zone [2, 0], the rotational velocity in these outer zones rapidly diverges from Keplerian motion and quickly becomes smaller with larger r, in accordance with the conservation of angular momentum [see Equation (4)]. This results in the much larger f values found in these zones compared with zone [2, 0]. However, as the poloidal velocity gradually increases and becomes dominant with increasing poloidal distance (that is, large r and z; e.g. zone [0, 3]), the line width broadens and the true value of f decreases.

Figure 4. Plot of f factors against inclination angle for wind zones [0, 3] (solid), [2, 0] (dashed), and [2, 3] (dotted) for the M95 (blue) and E04 (cyan) disk wind models.

If a fixed value of f is assumed, and the potential bias of orientation is ignored, then a large sample of quasars of the same mass will produce a broad distribution of black holes masses. To quantify the effect of the orientation dependence of f on the black hole mass estimation for a large sample of AGN, we calculated the differential probability of estimating a given black hole mass using the fixed mean f value from Collin et al. (2006). The results are shown in Figure 5. Since the differential probability increases with increasing inclination angle, the possibility of seeing closer to edge-on is higher, P(i) = sin(i). Therefore, broader profiles are more likely to be observed as they become dominant in edge-on viewing angle, and black hole masses will generally be overestimated.

Figure 5. Differential probability associated with black hole mass for the M95 (blue) and E04 (cyan) models using ⟨f⟩ values for mean spectrum from Collin et al. (2006). In these models, the true black hole mass is $10^{8}\,\text{M}_{\odot }$ . The shaded region represents the M _BH within one sigma range of the median (dashed). Left: Mean f factor using FWHM of $\langle f_{\text{FWHM(H$\beta $)}} \rangle =1.17$ . Right: Mean f factor using σ_line of $\langle f_{\sigma (\text{H}\beta )} \rangle =3.85$ .

This is more pronounced when using FWHM and in general, the masses determined from FWHM tend to be overestimated for both disk wind geometries. The median black hole mass recovered using the M95 model is $3.88^{+0.43}_{-1.31} \times 10^{8}\,\text{M}_{\odot }$ , approximately four times larger than the input black hole mass, and for the E04 model, the median recovered black hole mass is double the input mass with $1.97^{+0.22}_{-0.66} \times 10^{8}\,\text{M}_{\odot }$ .

The black hole masses obtained from σ_line (Figure 5, right) tend to be less biased and more accurate in general. However, the accuracy of the recovered mass was still found to be model dependent. The median black hole mass recovered for the M95 model of $1.37^{+0.15}_{-0.46} \times 10^{8}\,\text{M}_{\odot }$ is slightly overestimated, while the mass is underestimated in the E04 model with $0.72^{+0.08}_{-0.24} \times 10^{8}\,\text{M}_{\odot }$ .

4 DISCUSSION

Obtaining accurate black hole mass measurements is crucial for understanding the role of black hole growth in galaxy evolution. Therefore, it is important to understand how the geometry and inclination of the BLR, and the chosen line width measurement affect the accuracy in our mass estimation.

The range of f values can be much greater than the prescribed spread in the literature value. Therefore, we need to be cautious when using a single value of f as it may bias mass estimates especially when the inclination angle of the AGN is low. The M95 and E04 models establish relationships between the f factor and inclination angle (Figure 3, upper), in agreement with Pancoast et al. (2014) despite different modelling approach.

The BLR geometry, kinematics, and the origin of the emission line also affects the true f value for individual AGN. This is evident from the differences in the f values calculated for the different disk wind models, the offset between the disk wind models, the differences in the f values for the different wind zones, and the dynamical modelling results of Pancoast et al. (2014). The true nature of the BLR is unknown, and although some consistency is expected in the BLR, we currently cannot characterise the intrinsic distribution of f values for the whole AGN population. However, the differences in f due to the geometry and kinematics appears to be small compared to the effects of inclination angle. Also, our model assumes that the BLR is visible for all inclination angles. However, in the standard model of AGN, the BLR is believed to be obscured by a dusty torus. When this is taken into consideration, the estimate of the median black hole mass (Figure 5) is lowered as the probability of observing a closer to face-on AGN is increased.

Several studies have also investigated the scaling relationship between the f factor and inclination angle (Decarli et al. 2008; Kashi et al. 2013). Our predicted $f_{\text{FWHM}}$ values are consistent with the analytical prediction of f from Kashi et al. (2013) for a virialised line-driven disk wind model. However, the Decarli et al. (2008) predictions for a geometrically thin disk model better matches our findings for f _σ.

The line widths are typically measured using the FWHM or σ_line. As the FWHM is a zeroth moment of the line profile, the sensitivity to the line core is higher than it is in the line wings. In contrast, σ_line is a second moment of the line and is less affected by the line core. The σ_line from rms spectra is commonly employed as a proxy in calculating the black hole mass since it has been argued that this provides a smaller bias and a better fit to the virial relation (Peterson et al. 2004; Collin et al. 2006; Peterson 2011; Denney et al. 2013). We found that the black hole mass estimated using the $\langle f_{\sigma (\text{H}\beta )} \rangle$ is closer to the input black hole mass compared to $\langle f_{\text{FWHM(H$\beta $)}} \rangle$ value from Collin et al. (2006) (Figure 5). However, this discrepancy can be reduced when the shape corrections for $\langle f_{\text{FWHM(H$\beta $)}} \rangle$ , suggested by Collin et al. (2006), are taken into consideration. When both $\langle f_{\text{FWHM(H$\beta $)}} \rangle$ corrections (Equations 5 and 7; Collin et al. 2006) are applied, the median black hole mass for the M95 model is $1.66^{+0.19}_{-0.55} \times 10^{8}\,\text{M}_{\odot }$ , which is marginally consistent with the true mass and the mass estimate found using $\langle f_{\sigma (\text{H}\beta )} \rangle$ . For the E04 model, the recovered median black hole mass is $0.84^{+0.09}_{-0.28} \times 10^{8}\,\text{M}_{\odot }$ after the $\langle f_{\text{FWHM(H$\beta $)}} \rangle$ shape correction (Equation 5; Collin et al. 2006) and $0.94^{+0.06}_{-0.31} \times 10^{8}\,\text{M}_{\odot }$ using the FWHM width correction (Equation 7; Collin et al. 2006).

It is worth mentioning several caveats in our modelling approach. The disk wind model simulations presented are simplifications of the complex BLR. The line driving mechanisms of the wind or photoionisation physics are not included in this model. We have also made major assumptions about the wind dynamics in our models, such as the local mass loss rate and the wind acceleration profile. The effects of these assumptions have not been investigated in this work. Future work will systematically search the parameter space in order to refine the models and to obtain a better fit with observations.

5 SUMMARY

In this work, we have implemented a dynamical disk wind prescription to explore the influence of BLR orientation on the recovered black hole mass. The virial factor, f, which scales the line-of-sight virial product to the true black hole mass, is calculated using the disk wind model and compared to f values from the literature. It is evident that the black hole masses recovered depend on several factors: the BLR geometry and dynamics, the origin of the emission line, and the inclination angle. The observed trend with inclination angle agrees with the results of Pancoast et al. (2014) despite the different models investigated. Additionally, the spread in the model predicted f values significantly exceeds the spread prescribed for the empirically determined values of f from the literature. Therefore, using a single average value of f may instill a bias into the mass estimate for large AGN samples.

We also computed the black hole mass using literature values of f _σ and $f_{\text{FWHM}}$ from Collin et al. (2006). The black hole mass is closer to the true mass if the velocity dispersion is measured using the σ_line. Nevertheless, as suggested by Collin et al. (2006), the $f_{\text{FWHM}}$ can be corrected to improve the mass estimate.