Published online by Cambridge University Press: 11 April 2023
We present a new high-resolution neutral atomic hydrogen (Hi) survey of ring galaxies using the Australia Telescope Compact Array (ATCA). We target a sample of 24 ring galaxies from the Buta (1995) Southern Ring Galaxy Survey Catalogue in order to study the origin of resonance-, collisional- and interaction-driven ring galaxies. In this work, we present an overview of the sample and study their global and resolved Hi properties. In addition, we also probe their star formation properties by measuring their star formation rates (SFR) and their resolved SFR surface density profiles. We find that a majority of the barred galaxies in our sample are Hi-deficient, alluding to the effects of the bar in driving their Hi deficiency. Furthermore, for the secularly evolving barred ring galaxies in our sample, we apply Lindblad’s resonance theory to predict the location of the resonance rings and find very good agreement between predictions and observations. We identify rings of Hi gas and/or star formation co-located at one or the other major resonances. Lastly, we measure the bar pattern speed (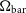 $\Omega_{\textrm{bar}}$) for a sub-sample of our galaxies and find that the values range from 10–90
$\Omega_{\textrm{bar}}$) for a sub-sample of our galaxies and find that the values range from 10–90 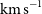 $\textrm{km s}^{-1}$kpc
$\textrm{km s}^{-1}$kpc $^{-1}$, in good agreement with previous studies.
$^{-1}$, in good agreement with previous studies.