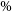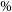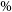Statistical analysis of kicked black holes from TNG300 simulation

Abstract

Asymmetric emission of gravitational waves during mergers of black holes (BHs) produces a recoil kick, which can set a newly formed BH on a bound orbit around the centre of its host galaxy, or even completely eject it. To study this population of recoiling BHs we extract properties of galaxies with merging BHs from Illustris TNG300 simulation and then employ both analytical and numerical techniques to model unresolved process of BH recoil. This comparative analysis between analytical and numerical models shows that, on cosmological scales, numerically modelled recoiling BHs have a higher escape probability and predict a greater number of offset active galactic nuclei (AGN). BH escaped probability $>$40% is expected in 25$\%$ of merger remnants in numerical models, compared to 8$\%$ in analytical models. At the same time, the predicted number of offset AGN at separations ${>}5$ kpc changes from 58$\%$ for numerical models to 3$\%$ for analytical models. Since BH ejections in major merger remnants occur in non-virialised systems, static analytical models cannot provide an accurate description. Thus we argue that numerical models should be used to estimate the expected number density of escaped BHs and offset AGN.

1. Introduction

The concept of hierarchical growth of structures suggests that galaxy mergers play an important role in their evolution. Alongside building their masses, galaxy mergers can reshape their structure, enhance star formation, and potentially trigger active galactic nuclei (AGN). Both theory and observations reveal the potential of major galaxy mergers to fuel enough gas to the central galaxy regions and increase the central black hole (BH) accretion rate (e.g. Cox et al. 2008; Lambas et al. 2012; Patton et al. 2013;Weston et al. 2017; Ellison et al. 2019; Rodríguez Montero et al. 2019; Byrne-Mamahit et al. 2022).

When two galaxies merge, the central BHs gradually lose energy and move towards the centre of the merged galaxy due to dynamical friction. This results in the formation of a binary BH, which can continue to harden through interactions with stars and gas. The formation of a close BH binary system is significantly affected by the morphology and mass ratio of progenitor galaxies. Major mergers of gas-rich galaxies are expected to result in effective hard BH binary formation (Escala et al. 2004, 2005; Mayer et al. 2007; Roškar et al. 2015; del Valle et al. 2015; Goicovic et al. 2017; Khan et al. 2016), while some minor mergers do not necessarily lead to central BHs merger (Callegari et al. 2009, 2011; Tremmel et al. 2018).

In the final stages of BH merger, the emission of gravitational waves will effectively remove angular momentum and energy from the binary system, leading to a rapid collision (Begelman, Blandford, & Rees 1980). Those gravitational waves could be directly detected with the upcoming space-based interferometer LISA (Laser Interferometer Space Antenna, Amaro-Seoane et al. 2022), whose focus will be on the mergers of BHs in the mass range $10^{4}$ – $10^{7} \>{\rm M_{\odot}}$ . Any asymmetry in the binary system, such as the presence of BHs with unequal masses or spins, can cause the asymmetric emission of gravitational radiation and BH recoil. The emission of gravitational waves has a preferred direction due to a non-zero net linear momentum, and this causes the centre of mass of the binary to move in the opposite direction (Redmount & Rees 1989). During this process, the newly formed BH receives a recoil whose amplitude depends on the mass ratio of the merging BH, the magnitude and orientation of their spins with respect to the binary’s orbital plane, and the eccentricity of the orbit. Mergers of fast rotating BHs with spin vectors in the orbital plane and orientated in opposite directions result with super-kicks as high as $4000\>{\rm km}\,{\rm s}^{-1}$ , while efficient spin alignment during BH merger reduces kick velocities (González et al. 2007; Campanelli et al. 2007; Lousto & Zlochower 2011).

Depending on the amplitude of the kick velocity, a recoiling BH could be either placed on a bound orbit around the galaxy centre or be completely ejected from its host. Bound BHs can spend up to several Gyr oscillating with low amplitude around the galaxy centre (e.g., Gualandris & Merritt 2008; Komossa & Merritt 2008), while this time can be significantly reduced in gas-rich systems (e.g., Blecha & Loeb 2008; Guedes et al. 2011; Sijacki et al. 2015). In the case that merged BH receives a recoil velocity higher than the escape velocity from the host galaxy, it will be completely ejected. Those wandering BHs are less likely to merge with other BHs; thus, gravitational wave recoil could have a negative influence on merger-driven BH growth (e.g., Haiman 2004; Merritt et al. 2004; Volonteri 2007). If active at the time of the merger, the accretion disc will be ejected along with a recoiling BH, during which time it can be observed as spatially or kinematically offset AGN (e.g. Madau & Quataert 2004; Loeb 2007; Blecha & Loeb 2008; Blecha et al. 2011). There is a large number of observed offset AGN candidates in the literature (e.g. Komossa, Zhou, & Lu 2008; Robinson et al. 2010; Jonker et al. 2010; Civano et al. 2010, 2012; Eracleous et al. 2012; Koss et al. 2014; Markakis et al. 2015; Chiaberge et al. 2017; Kalfountzou, Santos Lleo, & Trichas 2017). More recently, Stemo et al. (2021) composed a catalogue of 204 offset and dual AGN, using the Advanced Camera for Surveys Active Galactic Nuclei Catalog (Stemo et al. 2021) of AGNs observed by Hubble Space Telescope. However, none of these cases have been confirmed since alternative explanations, such as a binary BH system with only one active BH, cannot be ruled out.

Even though cosmological simulations provide a powerful tool to investigate the population of merging galaxies, the actual process of a BH merger cannot be simulated due to the resolution limits. Instead, the results of cosmological simulations are often combined with analytical models for unresolved processes. Blecha et al. (2016) investigated trajectories of recoiling BHs using Illustris cosmological simulations (Vogelsberger et al. 2014a,b; Genel et al. 2014; Sijacki, Springel, & Haehnelt 2011). By extracting properties of merging BHs and progenitor galaxies directly from the simulation, authors constructed analytical models of merger remnant galaxies to estimate escape velocities, BH kick velocities, and offset AGN distribution.

On the other hand, higher mass resolution achieved by simulations of isolated galaxies can provide more detailed insights into processes within the merger remnant galaxy. Smole, Micic, & Mitrašinović (2019) showed that numerical models provide a more realistic representation of merging galaxies compared to analytical models. Mass redistribution during interaction can lead to a 25 $\%$ lower escape velocities in numerical models of major merger remnant galaxies (for more details we refer to Methods).

In this work, we combine the results of a cosmological simulation on one side and isolated galaxy simulations on the other side. We apply the similar analysis described by Blecha et al. (2016) to state-of-the-art The Next Generation Illustris Simulations a (Illustris TNG) project (Springel et al. 2018;Naiman et al. 2018; Pillepich et al. 2018; Nelson et al. 2018; Marinacci et al. 2018). We employ the simulation with the largest volume, TNG300, to extract properties of galaxies with merging BHs. In addition to analytical models, we used the results of numerical simulation of isolated galaxy mergers in order to estimate escape velocities (Smole et al. 2019). We investigate the difference between the predicted number of recoiling BHs in analytical and numerical models on cosmological scales and estimate the probability for complete BH ejections during major galaxy mergers.

In Methods we introduce the employed techniques, together with data sets used in this work, and we describe their implementation in our methodology. Our findings are presented and discussed in Results. In Conclusions we summarise the main findings of this work and draw conclusions.

2. Methods

2.1. Illustris TNG300

In order to calculate the statistics of recoiling BHs in numerical and analytical models, we use publicly available data from Illustris TNG project (Springel et al. 2018; Naiman et al. 2018; Pillepich et al. 2018; Nelson et al. 2018; Marinacci et al. 2018). Illustris TNG cosmological hydrodynamical simulations of galaxy formation were performed using the arepo code (Springel 2010). The simulations were initialised at redshift $z = 127$ using Planck Collaboration et al. (2016) cosmological parameters: matter density $\Omega_{\rm{m}}=0.3089$ , baryon density $\Omega_{\rm{b}}=0.0486$ , dark energy density $\Omega_{\Lambda}=0.6911$ , Hubble constant $H_{\rm{0}} = 0.6774\, \rm{km}\,\rm{s}^{-1} \rm{Mpc}^{-1}$ , power spectrum normalisation $\sigma_{\rm{8}}=0.8159$ and a primordial spectral index $n_{\rm{s}} = 0.9667$ . For the analysis employed in this work we choose the simulation with the largest cosmological box $(\sim$ $300\, \rm{Mpc})^{3}$ , TNG300. Mass resolution for TNG300 simulation is $5.9 \times 10^7 \>{\rm M_{\odot}}$ for DM particles and $1.1 \times 10^7 \>{\rm M_{\odot}}$ for baryonic component.

Results of Illustris TNG300 simulation are stored in 100 snapshots, from redshift $z=20$ to $z=0$ . Snapshot files contain information about each particle in the simulation volume. In TNG300 simulation a BH particle with a seed mass of $1.18\times10^6\>{\rm M_{\odot}}$ is placed in each galaxy more massive than $7.8 \times 10^{10}\>{\rm M_{\odot}}$ , which do not already have a BH, and then allowed to grow via gas accretion and by mergers. BH accretion is modelled according to Eddington-limited Bondi accretion rate:

(1a) \begin{equation} \dot{M}_{\textrm{Bondi}} = \frac{4 \pi G^2 M_{\text{BH}}^2 \rho}{c_s^3}, \end{equation}

(1b) \begin{equation} \dot{M}_{\textrm{Edd}} = \frac{4 \pi G M_{\textrm{BH}} m_p}{\epsilon_r \sigma_{\rm T}} c, \end{equation}

(1c) \begin{equation}\dot{M} = \min\left( \dot{M}_{\textrm{Bondi}}, \dot{M}_{\text{Edd}} \right),\end{equation}

where $M_{\text{BH}}$ is BH mass, G is the gravitational constant, $\rho$ the kernel-weighted ambient density around the BH, $c_s$ the kernel-weighted ambient sound speed including the magnetic signal propagation speed, $m_p$ the proton mass, c the speed of light, $\epsilon_r = 0.2$ the BH radiative efficiency and $\sigma_{\rm T}$ the Thompson cross section. We refer to Weinberger et al. (2018) for more details about BH growth and the feedback processes included.

An additional supplementary data catalogue is available providing details of each BH-BH merger in the simulation, otherwise not available from the snapshots alone. This file contains information about both merging BH ID numbers (unique throughout the simulation), their masses immediately preceding the merger and snapshot during which, or immediately following, this merger event occurred.

The total number of BH merger events in Illustris TNG300 simulation is 590 328. First, we exclude all multiple mergers, that is all BHs that participate in more than one merger event per snapshot. In a simplified case during triple mergers, the lowest mass BH will be ejected while the remaining BHs will form a binary system. However, the dynamic of multiple BH systems requires complex treatment which is beyond the scope of this paper. Even though this excludes 144 048 merger pairs ( $\sim$ 24%), our main goal is to obtain the comparative statistics between analytical and numerical predictions. Thus, we limit our analysis to a smaller sample of single BH mergers for which we have well-studied analytical and numerical models.

The next step was to link all of the merging BHs from BH mergers supplementary catalogue with the associated subhaloes, that is, the host galaxies. First, we identify the host galaxies of each BH participating in the merger event at the snapshot preceding the merger, while BHs still occupy separate systems. Next, we follow backward the evolution of each host galaxy, from the snapshot preceding the BH merger to the snapshot when the galaxies first appeared in the simulation. This step is necessary in order to accurately determine the mass ratio of the merging galaxies, since in the snapshot preceding the BH merger host galaxies have already exchanged mass as a consequence of galaxy interaction. The mass ratio of the merging galaxies is calculated at the snapshot where the secondary, that is, less massive galaxy, has the maximum mass, thus prior mass loss due to galaxy merger. That snapshot is taken as the last snapshot before the galaxy interaction started. However, since a galaxy merger is a prolonged process, it is possible to imagine a scenario where one of the progenitor galaxies undergoes a new merger between the last snapshot before galaxy interaction and the snapshot of the BH merger. That merger would change the total mass and other properties of the progenitor galaxy. We limit our analysis to single mergers, thus we eliminate from our sample not only galaxies that undergo multiple mergers per snapshot but also galaxies that experience multiple mergers during galaxy interaction.

The additional selection criterion is imposed to ensure that each host galaxy is well resolved. Following Blecha et al. (2016) and Kelley, Blecha, & Hernquist (2017) we require that each progenitor galaxy, at the last snapshot before the galaxy interaction, has $M_{\textrm{DM}}>10^{10}\>{\rm M_{\odot}}$ and $M_{\textrm{star}}>10^8\>{\rm M_{\odot}}$ . In addition, we also limit the upper mass of the host galaxy to $M_{\textrm{DM}}<8\times10^{13}\>{\rm M_{\odot}}$ to exclude galaxy clusters (Paul et al. 2017).

As we will discuss in the following subsection, Smole et al. (2019) showed that escape velocities from minor merger remnants in analytical and numerical models do not differ significantly. In addition, since BH mass is expected to scale with the host galaxy mass, minor mergers would lead to the formation of low mass ratio BH binaries, and the expected kick velocity in such systems is not enough to eject the central BH (see the following subsections). Thus we limit our analysis to major merger remnants. Our final sample contains 46 031 major merger remnants or $\sim$ 8% of the total number of all BH mergers in TNG300 simulation.

2.2. BH escape velocities in analytical and numerical galaxy models

Smole et al. (2019) investigated differences between recoiling BHs in analytical and numerical potential using isolated N-body simulations performed with GADGET-2 code (Springel 2005). The authors constructed numerical models for a set of progenitor galaxies with different total masses and mass distributions within galaxy components and simulated galaxy mergers with various galaxy mass ratios. In addition, the authors constructed analytical models of merger remnant galaxies with the same characteristics as their numerical counterparts. The main goal was to compare escape velocities from numerical and analytical merger remnants. In numerical models, BH was represented as one massive particle placed at the merger remnant centre and its trajectory was followed directly from the simulation. In analytical models BH trajectory was numerically integrated, using leapfrog integration. Both analytical and numerical techniques result in the same value of escape velocity for isolated and virialised galaxies. However, galaxy mergers cause mass redistribution within merger remnants which reduces escape velocities in numerical models. During galaxy mergers energy of individual particles is not conserved. In the process called violent relaxation (Lynden-Bell 1967) weakly bound particles can escape the host galaxy potential, which results in mass loss during mergers. This process is not depicted in static analytical potential, making the evolving numerical model a more realistic description of dynamical processes in galaxies with merging BHs. As a consequence, Smole et al. (2019) showed that analytical models overestimate BH escape velocities. BH escape velocities in numerical major merger remnant galaxies can be up to 25 $\%$ lower compared to those in analytical models. However, this effect is predominantly limited to major mergers. During minor mergers, the secondary galaxy will experience significant mass redistribution, but its contribution to the total potential is not sufficient to influence escape velocities, leading to the similar escape velocities in numerical and analytical minor merger remnants.

Here, we use the results of the above work to make comparative statistics between recoiling BHs in TNG300 simulation, assuming analytical versus numerical models. We extract properties of merger remnant galaxies directly from the simulation. For the given merger remnant mass, its central BH mass, and the mass ratio of the merging galaxies, analytical and numerical escape velocities calculated by Smole et al. (2019) are extrapolated and assigned to each galaxy from our TNG300 sample.

2.3. BH kick velocities

After assigning escape velocities to each major merger remnant galaxy, the next step is to calculate kick velocities for each newly formed BH, adopting the method described by Micic, Holley-Bockelmann, & Sigurdsson (2011). Kick velocity depends on the merging BH mass ratio, their spin amplitude, and the alignment to the orbital angular momentum:

(2a) \begin{equation}V_{\mathrm{k}} = [(V_{m}+V_{\perp} \rm{cos}{\xi})^2+(V_{\perp} \sin{\xi})^2+(V_{\parallel})^2]^{1/2},\end{equation}

where

(2b) \begin{equation}V_{m} = A \frac{q^2 \left(1-q\right)}{\left(1+q\right)^5} \left[ 1+ B \frac{q}{\left(1+q\right)^2}\right],\end{equation}

(2c) \begin{equation}V_{\perp} = H \frac{q^2}{\left(1+q\right)^5} \left( \alpha_2^\parallel - q \alpha_1^\parallel\right),\end{equation}

and

(2d) \begin{equation}V_{\parallel} = K \cos\left(\Theta-\Theta_0\right) \frac{q^2}{\left(1+q\right)^5}\left( \alpha_2^\perp - q \alpha_1^\perp \right).\end{equation}

The fitting constants are A $=1.2 \times 10^{4} \>{\rm km}\,{\rm s}^{-1}$ , B $=-0.93$ , H $=(7.3 \pm 0.3) \times 10^{3} \>{\rm km}\,{\rm s}^{-1}$ , and K $\cos\left(\Theta-\Theta_0\right) =(6.0 \pm 0.1) \times 10^{4}$ ; q is the mass ratio of the merging BHs, $\alpha_{i=1,2}=\frac{S_{i}}{M_{i}}$ is the reduced spin parameter, $S_{i}$ is the spin angular momentum of BH, and the orientation of the merger is determined with angles $\Theta$ i $\xi$ . Following Micic et al. (2011) we calculate kick velocities for two distinct spin distributions. In both models, BH spin amplitudes are taken from a uniform distribution, while BH spin orientation depends on a model choice. In the first model, BH spin orientations are also taken from a uniform distribution (‘random’ model), while in the second model, BH spins are always aligned with the orbital angular moment of the binary (‘aligned’ model), which results in lower kick velocities. The mass ratio of the merging BHs is taken directly from the BH merger supplementary catalogue. BH kick velocities are sampled from one of those distributions using 10 000 realisations for each merging BH pair from our sample.

2.4. Escaped BHs versus Offset AGN statistics

Next, we compare the sampled kick velocities to the escape velocity from the merger remnant. Throughout this work we will refer to realisations with $v_{{k, i}}>v_{\textrm{esc}}$ ( $i\in[1,...,10000]$ ) as escaped BHs. The escape probability of a host galaxy is defined as the fraction of escaped BHs out of 10 000 realisations. Recoiling BHs with $v_{{k, i}}<v_{\textrm{esc}}$ will not be ejected from the galaxy, but they can spend an extended period of time oscillating around the galaxy centre. We refer to those as BHs on bound orbits. We use the term offset AGN to refer to both escaped BHs and BHs on bound orbits, thus all BHs with kick velocities large enough to displace BH from the centre of the galaxy.

In this work, we separately investigate the statistics of escaped BHs and offset AGN. Our main goal is to calculate the comparative statistics between analytical and numerical predictions on cosmological scales, using a sample of well-resolved major merger remnants from TNG300 simulation, that reside outside of galaxy clusters.

3. Results

3.1. Major merger remnants in TNG300

Fig. 1 shows the total mass of each progenitor galaxy as a function of the central BH mass. The colour bar indicates the estimated 2D density of data points. Our sample is dominated by lower mass galaxies, $M_{\textrm{gal}}< 5\times10^{11}\>{\rm M_{\odot}}$ , that host central BHs with masses $M_{\textrm{BH}}<10^7\>{\rm M_{\odot}}$ .

Figure 1. Total mass of progenitor galaxy as a function of the central BH mass.

Fig. 2 shows the distribution of merging BH mass ratio, divided by the total BH mass, for all mergers (solid lines) and for mergers occurring at $z<1$ (dashed lines). A lower fraction of high mass ratios at $z<1$ indicates that mergers of equal mass BHs were more common at high redshifts before multiple mergers and accretion led to BH growth. The distribution of all BHs (blue solid line), shows an increase towards equal mass mergers, while massive BHs show a flatter distribution. Dotted lines show merging BH mass ratios in Illustris simulation, calculated by Blecha et al. 2016. This distribution is flatter and with a higher fraction of low mass ratios. Assuming that central BH mass scales with the host galaxy mass, choosing only major galaxy mergers, as we did in our sample, would lead to higher BH mass ratios. A lower fraction of the most massive BHs reflects the imposed higher limit for total galaxy mass of $M_{\textrm{DM}}<8\times10^{13}\>{\rm M_{\odot}}$ , so we exclude galaxy clusters.

Figure 2. The distribution of merging BH mass ratio, for different total BH mass bins. Dashed lines represent the same distribution calculated for BH mergers at $z<1$ . Dotted lines show the distribution in Illustris simulation, calculated by Blecha et al. (2016).

Figure 3. Numerically calculated escape velocity as a function of redshift.

BH mergers at high redshifts are expected to produce more escaped BHs due to generally lower masses of merger remnant galaxies, and thus lower escape velocities. Fig. 3 shows escape velocities as a function of redshift, calculated using numerical models. As predicted by the hierarchical growth of structures, the number of high-mass galaxies with high escape velocities decreases with redshift as galaxies build their masses and thus potential wells deep enough to retain a recoiling BH.

For the extracted galaxy mass, its central BH mass, and the mass ratio of the merging galaxies we estimate the escape velocity for each galaxy in our sample using the results obtained by Smole et al. (2019). Fig. 4 shows escape velocities from galaxies in analytical models as a function of their escape velocities in numerical models. The colour bar indicates the estimated 2D density of data points on a logarithmic scale. The black dashed line represents a linear fit to our data, while the solid red line denotes $v_{\textrm{esc (an.)}}=v_{\textrm{esc (num.)}}$ . The majority of galaxies from our sample occupy the region above the red line, thus on a statistical level numerical models of major merger remnants predict lower escape velocities compared to analytical models.

Figure 4. Escape velocities from galaxies in analytical models as a function of their escape velocities in numerical models. The black dashed line represents a linear fit to our data and the solid red line denotes $v_{\textrm{esc (an.)}}=v_{\textrm{esc (num.)}}$ .

In this work, we adopted the method described by Micic et al. (2011) to calculate kick velocities of merged BHs. Fig. 5 shows the distribution of kick velocities from our data set, as a function of the merging BH mass ratio. Values of kick velocities are the result of 10 000 realisations per merger event, in which BH spins are sampled from random or from aligned distribution. If BH spins prior BH merger are drawn from a uniform distribution (random model, black vertical lines) the resulting kick velocities can be $>$ $2000\,\textrm{km\,s}^{-1}$ , which is enough to eject central BH even from the most massive galaxies in our sample. On the other hand, if BH spins are always aligned with the orbital angular moment of the binary (aligned model, red horizontal lines), the highest possible kick velocities are $\sim$ 250 km s $^{-1}$ and recoiling BH are expected to be rare. Both distributions yield the highest kick velocities for mergers of BHs with comparable masses.

Figure 5. Distribution of kick velocities as a function of the mass ratio of merging BHs. Black vertical lines represent random spin model, while red horizontal lines denote to aligned spin model.

Figure 6. Probability function for a BH to escape for random spin model of BH kick velocity distribution. Different colours indicate numerical (solid line, pink) or analytical (dashed line, cyan) values for escape velocity calculation.

3.2. Statistics of escaped BHs

Next, we calculate the probability that each BH merger pair from our sample produces a kick large enough for complete BH removal. For each merger event, BH kick velocities are sampled from either random or aligned spin distribution using 10 000 realisations. Escape probability, or the probability for each merger event to completely eject BH, is calculated by comparing each of the sampled kick velocities $v_{{k, i}}$ ( $i\in[1,\,...\,,10000]$ ) to the escape velocity from the merger remnant. Realisations with $v_{{k, i}}>v_{\textrm{esc}}$ are referred to as escaped BHs.

Figure 7. Same as Fig. 6, for different redshift bins.

Fig. 6 shows BH escape probability adopting random spin model for BH kick velocity distribution. Different colours correspond to different models used to estimate the escape velocity from the merger remnant galaxy, numerical (solid line, pink), and analytical (dashed, cyan). If the BH spin parameters are taken from a uniform distribution, the maximal probability for escaped BH is $\sim$ 67% and $\sim$ 55% for numerical and analytical models, respectively. Both models predict that the majority of merger events from our sample would not lead to BH removal, however, both distributions show a local maximum value around $\sim$ 40% (numerical) and $\sim$ 35% (analytical). Thus, the plot shows that the model with numerically estimated escape velocities results in a higher probability for escaped BHs compared to the analytical model.

Under the assumption that BH spins are always aligned with the orbital angular moment of the binary (aligned spin model), resulting kick velocities are lower (Fig. 5). In fact, our sample does not contain any escaped BHs for the analytical model for escape velocity, while numerical model predicts the highest probability of $\sim$ 2% for a merger event to remove BH. Thus, if BH spin alignment during BH mergers is efficient, ejection of a newly formed BH from its host potential well is not excepted.

Further, we explore how the probability that a BH merger will produce an escaped BH evolves with time. Fig. 7 shows BH probability to escape for different redshift bins. At redshifts $z>5$ escaped BH probability function peaks close to 40 $\%$ , followed by a bimodal distribution at redshifts $1<z<4$ , with the second peak at zero probability. At low redshifts the function shows one peak and our sample is dominated by BH mergers that will not lead to BH removal. Again, for each redshift bin escaped BH probability function is shifted towards higher values when numerical models are used.

Table 1 shows the total number of BH mergers that have escape probability $>$ 20% and $>$ 40%, assuming analytical versus numerical potential. Random spin model predicts that over $50 \%$ of BH mergers from our sample, produce a BH with escape probability $>$ 20% for both numerical and analytical models. However, at higher escape probabilities the difference between our models becomes significant. Numerical models predict that $25 \%$ of BH mergers leave a remnant BH with escape probability $>$ 40%, compared to 8% in analytical models. Under the assumption that BH spins are aligned, escape probabilities $>$ 2% are not expected.

Table 1. Total number of escaped BHs.

Similarly, Table 2 shows the total number of BH mergers with escape probability $>$ 20% and $>$ 40%, per redshift bin. The results presented here refer to random model of spin distribution. At each redshift bin, numerical models produce a higher fraction of BH mergers with escape probability exceeding 40%. Moreover, the gap between the fraction of escaped BHs predicted analytically versus numerically widens as redshift increases. This is a consequence of generally more turbulent galaxy evolution at higher redshifts, with numerous mergers occurring before galaxies acquire sufficient mass to retain the majority of recoiled BHs. Numerical models better capture these processes in merging galaxies and thus provide a more accurate estimate of the number of escaped BHs. If an offset AGN is defined as a kicked BH with escape probability $>$ 40%, numerical models predict a substantially more significant number of BH ejected from the host galaxy centre, compared to analytical models. However, the gap between the two models becomes less pronounced when considering an escape probability $>$ 20%.

Table 2. Total number of escaped BHs per redshift bin.

Fig. 8 shows the median escape probability as a function of redshift, for numerical (red) and analytical (blue) models. The median probability that a BH merger pair would produce an escaped BH increases with redshift. At high redshifts a greater percentage of BH mergers are expected to result in kick velocities high enough to eject central BH.

Figure 8. Median escape probability as a function of redshift. Kick velocities are calculated assuming random spin distribution.

3.3. Statistics of offset AGN

Further, we explore the distribution of offset AGN, thus we also take into account recoiling BHs with kick velocities lower than the escape velocity, but potentially still high enough to produce a spatial offset. Since Blecha et al. (2016) provided a similar distribution for the Illustris sample, we reproduce their Fig. 4 and compare our results. Fig. 9 shows the distribution of median kick velocity for a BH merger pair, scaled to the host escape velocity in numerical (solid line) and analytical (dashed line) models. The distribution is separated by total BH mass, indicated by different colours. Blue line ( $\log(M_{\textrm{BH,tot}}/\>{\rm M_{\odot}})>6$ ) shows all BH mergers in our sample. A greater fraction of escaped BHs is predicted for low-mass BHs, while complete BH ejections of most massive BHs are not expected. However, the plot shows the median kick velocity obtained after 10 000 realisations. Assuming random spin distribution even the most massive BHs occasionally get kick velocities large enough for complete ejection from their hosts. If BH spins are aligned, kick velocities $\log(v_{k, \textrm{median}}/v_{\textrm{esc}})>-0.5$ are possible only for the lowest mass BHs. Regardless of the total BH mass and the chosen model for BH spin distribution, numerical models always predict a greater number of offset AGN.

Figure 9. The distribution of $\log(v_{k,\textrm{median}}/v_{\textrm{esc}})$ ratio for random (left panel) and aligned (right panel) spin distributions. Solid and dashed lines denote numerically and analytically calculated escape velocities, respectively. Different colours indicate the total merging BH mass bins. The dotted line represents the distribution obtained by Blecha et al. (2016). For kick velocities $v_{k,\textrm{median}}<v_{\textrm{esc}}$ our models predict a greater number of offset AGN.

Dotted lines on Fig. 9 represent the distribution obtained by Blecha et al. (2016), assuming random and aligned spin distributions. Our models predict a greater fraction of BHs with kick velocities $v_{k,\textrm{median}}<v_{\textrm{esc}}$ . Recoiled BHs in range $\log v_{k, \textrm{median}}/v_{\textrm{esc}} \in (-0.5,1)$ are expected to produce offset AGN that can spend a significant time on bound orbits, thus our models predict a greater number of offset AGN compared to the findings of Blecha et al. (2016). However, we note that our results cannot be compared directly, since our sample contains only major galaxy mergers from TNG300 simulation, while Blecha et al. (2016) shows the distribution of galaxy mergers with all mass ratios from lower volume cube of Illustris simulation. In fact, distributions calculated in this work predict a higher fraction of offset AGN, using both analytical and numerical estimates for the escape velocity. This indicates that the values of kick velocities in our sample are higher. Alongside BH spin parameters, the mass ratio of merging BHs plays a key role in the resulting kick velocity amplitude. Fig. 5 shows that the highest kick velocities can be achieved in mergers of BHs with comparable masses. In contrast, mergers of low mass ratio binaries result in low kick velocities and escaped BHs in such systems are expected to be rare. As shown in Fig. 2 the distribution of merging BH mass ratios from our sample has a lower fraction of low mass ratios compared to Blecha et al. (2016) sample. By including only major mergers in our sample, we have introduced a preference for higher kick velocities. Again, a lower fraction of most massive BHs in our sample reflects the imposed upper limit for host galaxy mass of $M_{\textrm{DM}}<8\times10^{13}\>{\rm M_{\odot}}$ .

Next, we explore the maximal distance from a galaxy centre reached by recoiled BH, assuming the median value of kick velocity. Fig. 10 shows the maximal separation from a galaxy centre as a function of $v_{k, \textrm{median}}/v_{\textrm{esc}}$ ratio. Maximal distances from the host centre that BHs could reach in our analytical models (left panel) are in agreement with Blecha et al. (2016) predictions (red lines). Recoiled BHs from both TNG300 (this work) and Illustris (Blecha et al. 2016) samples will reach comparable separations if their trajectories are calculated analytically. This agreement is anticipated as we employ similar analytical models. In numerical models (right panel), due to the violent relaxation process, redistribution of mass within the merger remnant galaxies will allow recoiled BHs to reach greater separations. BHs on larger galactocentric distances also spend more time on bound orbits outside of the galactic centre, thus for the given $v_{k, \textrm{median}}/v_{\textrm{esc}}$ ratio numerical models predict more spatially offset AGNs.

Figure 10. Maximal separation from a galaxy centre reached by a recoiled BH as a function of $v_{k, \textrm{median}}/v_{\textrm{esc}}$ ratio for analytical (left) and numerical (right) models. Red lines represent the upper and lower limits of the distribution obtained by Blecha et al. (2016).

Table 3 shows the total number of recoiled BHs at separations $>$ 5 and $>$ 20 kpc per redshift bin, assuming numerical versus analytical models. For a median value of kick velocity majority of recoiled BHs will reach separations $>$ 5 kpc in numerical models, in contrast to analytical models where $\ge$ 90% BHs will stay bound to central galaxy regions. The total number of offset AGN, as well as the difference between analytical and numerical models, increases with redshift, which reflects the hierarchical growth of structures and a greater number of low-mass galaxies in the early Universe.

Table 3. Total number of offset AGN.

4. Conclusions

Static analytical models of merger remnant galaxies have been widely used to study recoiling BHs (e.g. Blecha et al. 2016). However, Smole et al. (2019) suggested that numerical models represent more realistic approach since galaxy mergers can lead to a decrease in galaxy mass via violent relaxation process that is not depicted in static analytical models. The authors showed that escape velocities in numerical models can be up to 25 $\%$ lower compared to those in analytical models.

Here, we extended the above work and investigated the comparative statistics between recoiling BHs in analytical and numerical models of galaxies extracted from TNG300 simulation. Our sample consisted of 46 031 well-resolved major merger remnant galaxies outside galaxy clusters. For the given merger remnant galaxy mass, central BH mass, and mass ratio of progenitor galaxies we estimated analytical and numerical escape velocities, extrapolating the escape velocities calculated by Smole et al. (2019). Kick velocities are calculated using the method described by Micic et al. (2011). For each merging BH pair from our sample, BH spins are sampled from random or aligned spin distributions, using 10 000 realisations. Comparing kick velocities to the escape velocity from the host galaxy, we are able to distinguish between recoiled BHs on bound orbits and escaped BHs.

If BH spins are taken from random spin distribution, numerical models predict that 25 $\%$ of merging BHs from our sample will have escape probability $>$ 40%, compared to 8% for analytical models. On the other hand, aligned spin distribution does not yield kick velocities large enough to produce escaped BHs. As redshift increases, the disparity between analytical and numerical models becomes more prominent, highlighting the turbulent evolution of galaxies at high redshifts. Processes in merging galaxies cannot be described using static analytical models alone, thus numerical models provide a better estimate of the number of escaped BHs.

High escape probabilities predicted by numerical models can have a negative influence on BH growth through mergers. Major merges of gas reach galaxies can fuel gas into central galaxy regions, trigger episodes of gas accretion and exponential BH growth. At redshifts $z>5$ , $\sim$ 40% of major mergers in numerical models will produce a recoiling BH with escape probability $>$ 40%. This makes merger-driven BH growth at high redshifts challenging. However, if a kicked BH remains bound, future mergers are less likely to eject it since escape probability decreases at lower redshifts, as galaxies build their mass. For aligned BH spin model, kick amplitudes are not high enough to halt BH growth through mergers, since neither numerical nor analytical models produce recoiling BHs with escape probability $>$ 2%.

Numerical models also predict a greater number of offset AGN. For any given fraction of the escape velocity, recoiled BHs in numerical models are able to reach greater distances from the host centre, increasing the probability of their detection. Assuming median values of kick velocity numerical models predict that 58 $\%$ of BH mergers in our sample would produce kicks large enough to displace BHs at separations $>$ 5 kpc in numerical models, while analytical models predict only 3 $\%$ of BHs at those separations. Recoiled BHs with larger spatial offsets also have longer return times, which prolongs the period during which they could possibly be observed.

Thus, on cosmological scales, numerically modelled recoiling BHs have a higher escape probability and predict a greater number of offset AGN. We conclude that numerical models should be favoured over analytical ones since BH ejections take place in non-virialised merger remnants.