Introduction
Biomolecular condensates are membraneless organelles within the cell that are thought to form via phase separation of proteins and nucleic acids (Brangwynne et al., Reference Brangwynne, Eckmann, Courson, Rybarska, Hoege, Gharakhani, ulicher and Hyman2009; Banani et al., Reference Banani, Lee, Hyman and Rosen2017; Boeynaems et al., Reference Boeynaems, Holehouse, Weinhardt, Kovacs, Van Lindt, Larabell, Van Den Bosch, Das, Tompa, Pappu and Gitler2019; Mittag and Pappu, Reference Mittag and Pappu2022). Intrinsically disordered proteins are found ubiquitously in naturally occurring phase-separating proteins and the flexible nature of these proteins promotes transient interactions required for phase separation (Jonas and Izaurralde, Reference Jonas and Izaurralde2013; Malinovska et al., Reference Malinovska, Kroschwald and Alberti2013; Quiroz and Chilkoti, Reference Quiroz and Chilkoti2015; Schmidt and Görlich, Reference Schmidt and Görlich2015; Uversky et al., Reference Uversky, Kuznetsova, Turoverov and Zaslavsky2015; Pak et al., Reference Pak, Kosno, Holehouse, Padrick, Mittal, Ali, Yunus, Liu, Pappu and Rosen2016; Harmon et al., Reference Harmon, Holehouse, Rosen and Pappu2017; Dignon et al., Reference Dignon, Zheng, Best, Kim and Mittal2018; Schuster et al., Reference Schuster, Dignon, Tang, Kelley, Ranganath, Jahnke, Simpkins, Regy, Hammer, Good and Mittal2020). Mutational studies have shown that
![]() $ \pi $
–
$ \pi $
–
![]() $ \pi $
(aromatic–aromatic) and cation–
$ \pi $
(aromatic–aromatic) and cation–
![]() $ \pi $
(cation–aromatic) interactions promote biomolecular phase separation, especially those involving tyrosine (Y), phenylalanine (F), and arginine (R) (Nott et al., Reference Nott, Petsalaki, Farber, Jervis, Fussner, Plochowietz, Craggs, Bazett-Jones, Pawson, Forman-Kay and Baldwin2015; Brady et al., Reference Brady, Farber, Sekhar, Lin, Huang, Bah, Nott, Chan, Baldwin, Forman-Kay and Kay2017; Lin et al., Reference Lin, Currie and Rosen2017; Qamar et al., Reference Qamar, Wang, Randle, Ruggeri, Varela, Lin, Phillips, Miyashita, Williams, Ströhl, Meadows, Ferry, Dardov, Tartaglia, Farrer, Schierle, Kaminski, Holt, Fraser, Schmitt-Ulms, Klenerman, Knowles, Vendruscolo and St George-Hyslop2018; Wang et al., Reference Wang, Choi, Holehouse, Lee, Zhang, Jahnel, Maharana, Lemaitre, Pozniakovsky, Drechsel, Poser, Pappu, Alberti and Hyman2018; Fisher and Elbaum-Garfinkle, Reference Fisher and Elbaum-Garfinkle2020; Greig et al., Reference Greig, Nguyen, Lee, Holehouse, Posey, Pappu and Jedd2020; Martin et al., Reference Martin, Holehouse, Peran, Farag, Incicco, Bremer, Grace, Soranno, Pappu and Mittag2020; Bremer et al., Reference Bremer, Farag, Borcherds, Peran, Martin, Pappu and Mittag2022). In addition, it has been demonstrated that some residues act as ‘stickers’ and promote phase separation, while other residues known as ‘spacers’ favour the solubility of proteins (Harmon et al., Reference Harmon, Holehouse, Rosen and Pappu2017, Reference Harmon, Holehouse and Pappu2018; Holehouse and Pappu, Reference Holehouse and Pappu2018a). While at first glance, some stickers may contain similar functional groups, they can be unequal contributors to biomolecular phase separation. For instance, Y is better than F and R is better than lysine (K) in stabilising condensates (Nott et al., Reference Nott, Petsalaki, Farber, Jervis, Fussner, Plochowietz, Craggs, Bazett-Jones, Pawson, Forman-Kay and Baldwin2015; Brady et al., Reference Brady, Farber, Sekhar, Lin, Huang, Bah, Nott, Chan, Baldwin, Forman-Kay and Kay2017; Lin et al., Reference Lin, Currie and Rosen2017; Qamar et al., Reference Qamar, Wang, Randle, Ruggeri, Varela, Lin, Phillips, Miyashita, Williams, Ströhl, Meadows, Ferry, Dardov, Tartaglia, Farrer, Schierle, Kaminski, Holt, Fraser, Schmitt-Ulms, Klenerman, Knowles, Vendruscolo and St George-Hyslop2018; Wang et al., Reference Wang, Choi, Holehouse, Lee, Zhang, Jahnel, Maharana, Lemaitre, Pozniakovsky, Drechsel, Poser, Pappu, Alberti and Hyman2018; Fisher and Elbaum-Garfinkle, Reference Fisher and Elbaum-Garfinkle2020; Greig et al., Reference Greig, Nguyen, Lee, Holehouse, Posey, Pappu and Jedd2020; Martin et al., Reference Martin, Holehouse, Peran, Farag, Incicco, Bremer, Grace, Soranno, Pappu and Mittag2020; Bremer et al., Reference Bremer, Farag, Borcherds, Peran, Martin, Pappu and Mittag2022). R may also modulate phase separation in a context-dependent manner (Bremer et al., Reference Bremer, Farag, Borcherds, Peran, Martin, Pappu and Mittag2022). Some of these observations raise an important question: what are the key features that characterise the underlying energy landscapes of phase-separating proteins? In this paper, we address this question by applying the energy landscape framework to peptides with different sequences encoding
$ \pi $
(cation–aromatic) interactions promote biomolecular phase separation, especially those involving tyrosine (Y), phenylalanine (F), and arginine (R) (Nott et al., Reference Nott, Petsalaki, Farber, Jervis, Fussner, Plochowietz, Craggs, Bazett-Jones, Pawson, Forman-Kay and Baldwin2015; Brady et al., Reference Brady, Farber, Sekhar, Lin, Huang, Bah, Nott, Chan, Baldwin, Forman-Kay and Kay2017; Lin et al., Reference Lin, Currie and Rosen2017; Qamar et al., Reference Qamar, Wang, Randle, Ruggeri, Varela, Lin, Phillips, Miyashita, Williams, Ströhl, Meadows, Ferry, Dardov, Tartaglia, Farrer, Schierle, Kaminski, Holt, Fraser, Schmitt-Ulms, Klenerman, Knowles, Vendruscolo and St George-Hyslop2018; Wang et al., Reference Wang, Choi, Holehouse, Lee, Zhang, Jahnel, Maharana, Lemaitre, Pozniakovsky, Drechsel, Poser, Pappu, Alberti and Hyman2018; Fisher and Elbaum-Garfinkle, Reference Fisher and Elbaum-Garfinkle2020; Greig et al., Reference Greig, Nguyen, Lee, Holehouse, Posey, Pappu and Jedd2020; Martin et al., Reference Martin, Holehouse, Peran, Farag, Incicco, Bremer, Grace, Soranno, Pappu and Mittag2020; Bremer et al., Reference Bremer, Farag, Borcherds, Peran, Martin, Pappu and Mittag2022). In addition, it has been demonstrated that some residues act as ‘stickers’ and promote phase separation, while other residues known as ‘spacers’ favour the solubility of proteins (Harmon et al., Reference Harmon, Holehouse, Rosen and Pappu2017, Reference Harmon, Holehouse and Pappu2018; Holehouse and Pappu, Reference Holehouse and Pappu2018a). While at first glance, some stickers may contain similar functional groups, they can be unequal contributors to biomolecular phase separation. For instance, Y is better than F and R is better than lysine (K) in stabilising condensates (Nott et al., Reference Nott, Petsalaki, Farber, Jervis, Fussner, Plochowietz, Craggs, Bazett-Jones, Pawson, Forman-Kay and Baldwin2015; Brady et al., Reference Brady, Farber, Sekhar, Lin, Huang, Bah, Nott, Chan, Baldwin, Forman-Kay and Kay2017; Lin et al., Reference Lin, Currie and Rosen2017; Qamar et al., Reference Qamar, Wang, Randle, Ruggeri, Varela, Lin, Phillips, Miyashita, Williams, Ströhl, Meadows, Ferry, Dardov, Tartaglia, Farrer, Schierle, Kaminski, Holt, Fraser, Schmitt-Ulms, Klenerman, Knowles, Vendruscolo and St George-Hyslop2018; Wang et al., Reference Wang, Choi, Holehouse, Lee, Zhang, Jahnel, Maharana, Lemaitre, Pozniakovsky, Drechsel, Poser, Pappu, Alberti and Hyman2018; Fisher and Elbaum-Garfinkle, Reference Fisher and Elbaum-Garfinkle2020; Greig et al., Reference Greig, Nguyen, Lee, Holehouse, Posey, Pappu and Jedd2020; Martin et al., Reference Martin, Holehouse, Peran, Farag, Incicco, Bremer, Grace, Soranno, Pappu and Mittag2020; Bremer et al., Reference Bremer, Farag, Borcherds, Peran, Martin, Pappu and Mittag2022). R may also modulate phase separation in a context-dependent manner (Bremer et al., Reference Bremer, Farag, Borcherds, Peran, Martin, Pappu and Mittag2022). Some of these observations raise an important question: what are the key features that characterise the underlying energy landscapes of phase-separating proteins? In this paper, we address this question by applying the energy landscape framework to peptides with different sequences encoding
![]() $ \pi $
–
$ \pi $
–
![]() $ \pi $
and cation–
$ \pi $
and cation–
![]() $ \pi $
interactions that are known to promote phase separation of proteins yielding biomolecular condensates. The energy landscape framework allows us to explore the potential energy landscape of the peptides by performing geometry optimisation to identify local minima and transition states, and connecting them via steepest-descent pathways (Wales, Reference Wales2003). This approach provides a powerful tool to explain emergent observable properties in terms of the atomic interactions at a fundamental level.
$ \pi $
interactions that are known to promote phase separation of proteins yielding biomolecular condensates. The energy landscape framework allows us to explore the potential energy landscape of the peptides by performing geometry optimisation to identify local minima and transition states, and connecting them via steepest-descent pathways (Wales, Reference Wales2003). This approach provides a powerful tool to explain emergent observable properties in terms of the atomic interactions at a fundamental level.
Specifically, we performed a computational analysis of the potential energy landscape for various hexapeptide monomers modelled at the atomistic scale. We chose hexapeptides because the secondary structure of pentapeptides is context-dependent, that is, the same sequence of five amino acids can occur in different secondary structures, such as
![]() $ \alpha $
-helix and
$ \alpha $
-helix and
![]() $ \beta $
-sheet (Kabsch and Sander, Reference Kabsch and Sander1984). Therefore, hexapeptides may represent the minimal system useful for investigating the conformational properties of peptides, as well as the intramolecular interactions between the amino acids within a peptide monomer. In the stickers-and-spacers model, the ‘stickers’ are the interaction sites that can either be single amino acids, groups of residues, or entire domains that promote phase separation, and ‘spacers’ favour the solubility of proteins (Harmon et al., Reference Harmon, Holehouse, Rosen and Pappu2017; Holehouse and Pappu, Reference Holehouse and Pappu2018b; Yang et al., Reference Yang, Jones, Dao and Castañeda2019). Following the stickers-and-spacers model, the hexapeptides are chosen to contain two dipeptide stickers joined together by a glycine–glycine (GG) spacer (Abbas et al., Reference Abbas, Lipiński, Nakashima, Huck and Spruijt2021). Working with such minimal systems allows us to directly link the differences in the energy landscapes to specific interactions between amino acid pairs, and hence, reduce the impact of cooperative and competitive effects.
$ \beta $
-sheet (Kabsch and Sander, Reference Kabsch and Sander1984). Therefore, hexapeptides may represent the minimal system useful for investigating the conformational properties of peptides, as well as the intramolecular interactions between the amino acids within a peptide monomer. In the stickers-and-spacers model, the ‘stickers’ are the interaction sites that can either be single amino acids, groups of residues, or entire domains that promote phase separation, and ‘spacers’ favour the solubility of proteins (Harmon et al., Reference Harmon, Holehouse, Rosen and Pappu2017; Holehouse and Pappu, Reference Holehouse and Pappu2018b; Yang et al., Reference Yang, Jones, Dao and Castañeda2019). Following the stickers-and-spacers model, the hexapeptides are chosen to contain two dipeptide stickers joined together by a glycine–glycine (GG) spacer (Abbas et al., Reference Abbas, Lipiński, Nakashima, Huck and Spruijt2021). Working with such minimal systems allows us to directly link the differences in the energy landscapes to specific interactions between amino acid pairs, and hence, reduce the impact of cooperative and competitive effects.
A key signature of the energy landscape of a molecule is its heat capacity (
![]() $ {C}_V $
). Previous simulations of clusters have shown that low-temperature peaks in
$ {C}_V $
). Previous simulations of clusters have shown that low-temperature peaks in
![]() $ {C}_V $
represent solid–solid transitions between alternative low-energy conformations that differ significantly in terms of their enthalpy and entropy (Doye and Wales, Reference Doye and Wales1995, Reference Doye and Wales1998; Doye et al., Reference Doye, Wales and Miller1998; Doye and Calvo, Reference Doye and Calvo2002; Bogdan et al., Reference Bogdan, Wales and Calvo2006). In this contribution, we exploit the capability to produce rapid analysis of the heat capacity and assign the peaks to specific local minima with distinct intramolecular interactions. Measurement of
$ {C}_V $
represent solid–solid transitions between alternative low-energy conformations that differ significantly in terms of their enthalpy and entropy (Doye and Wales, Reference Doye and Wales1995, Reference Doye and Wales1998; Doye et al., Reference Doye, Wales and Miller1998; Doye and Calvo, Reference Doye and Calvo2002; Bogdan et al., Reference Bogdan, Wales and Calvo2006). In this contribution, we exploit the capability to produce rapid analysis of the heat capacity and assign the peaks to specific local minima with distinct intramolecular interactions. Measurement of
![]() $ {C}_V $
, as a function of temperature, can be useful to gain better insight into the thermodynamic properties of biopolymers, using differential scanning calorimetry (Benzinger, Reference Benzinger1971; Poland, Reference Poland2001, Reference Poland2002; Prabhu and Sharp, Reference Prabhu and Sharp2005; Cooper, Reference Cooper2010). In general, low temperature
$ {C}_V $
, as a function of temperature, can be useful to gain better insight into the thermodynamic properties of biopolymers, using differential scanning calorimetry (Benzinger, Reference Benzinger1971; Poland, Reference Poland2001, Reference Poland2002; Prabhu and Sharp, Reference Prabhu and Sharp2005; Cooper, Reference Cooper2010). In general, low temperature
![]() $ {C}_V $
measurement is useful for entropy calculation (Giauque and Johnston, Reference Giauque and Johnston1929) and for accessing vibrational modes of the molecule that are otherwise inaccessible to spectroscopic techniques that provide information about optical vibrational modes. These modes provide information about molecular conformations and stabilising interactions (Mrevlishvili, Reference Mrevlishvili1979). Even though biological molecules are not functional at extreme temperatures, thermodynamic analysis can offer new insights into the properties and behaviour that may have relevance at physiological temperatures. This analysis is similar to the study of crystalline (Starkweather, Reference Starkweather1960) and amorphous polymers at low temperatures (Warfield and Petree, Reference Warfield and Petree1962). Specific heat measurements for peptides at low temperatures (1.8–20 K) can be employed as a measure of the elasticity of the molecule (Finegold and Cude, Reference Finegold and Cude1972). Here, we calculate the
$ {C}_V $
measurement is useful for entropy calculation (Giauque and Johnston, Reference Giauque and Johnston1929) and for accessing vibrational modes of the molecule that are otherwise inaccessible to spectroscopic techniques that provide information about optical vibrational modes. These modes provide information about molecular conformations and stabilising interactions (Mrevlishvili, Reference Mrevlishvili1979). Even though biological molecules are not functional at extreme temperatures, thermodynamic analysis can offer new insights into the properties and behaviour that may have relevance at physiological temperatures. This analysis is similar to the study of crystalline (Starkweather, Reference Starkweather1960) and amorphous polymers at low temperatures (Warfield and Petree, Reference Warfield and Petree1962). Specific heat measurements for peptides at low temperatures (1.8–20 K) can be employed as a measure of the elasticity of the molecule (Finegold and Cude, Reference Finegold and Cude1972). Here, we calculate the
![]() $ {C}_V $
of peptide monomers using the harmonic superposition approximation (Wales, Reference Wales2017), and we observe features (peaks or inflection points) at low temperatures for the hexapeptides with phase separation promoting residues. The low-temperature peaks arise from competing structural motifs for a relatively small number of low-lying local minima. Peaks can be assigned to competition between these minima using the temperature derivative of the occupation probability (Wales, Reference Wales2017). The theory provides an exact decomposition of
$ {C}_V $
of peptide monomers using the harmonic superposition approximation (Wales, Reference Wales2017), and we observe features (peaks or inflection points) at low temperatures for the hexapeptides with phase separation promoting residues. The low-temperature peaks arise from competing structural motifs for a relatively small number of low-lying local minima. Peaks can be assigned to competition between these minima using the temperature derivative of the occupation probability (Wales, Reference Wales2017). The theory provides an exact decomposition of
![]() $ {C}_V $
in terms of local minima within the same approximation, which reveals the important cases of interest, where the peaks arise from competition between a few low-energy conformations. We emphasise that peaks in
$ {C}_V $
in terms of local minima within the same approximation, which reveals the important cases of interest, where the peaks arise from competition between a few low-energy conformations. We emphasise that peaks in
![]() $ {C}_V $
are simply being used as a diagnostic of the structure in the underlying landscape. This structure is clear in the harmonic normal mode approximation to the partition function; a more accurate treatment of
$ {C}_V $
are simply being used as a diagnostic of the structure in the underlying landscape. This structure is clear in the harmonic normal mode approximation to the partition function; a more accurate treatment of
![]() $ {C}_V $
is not required to achieve this diagnostic.
$ {C}_V $
is not required to achieve this diagnostic.
The degree of frustration (Bryngelson and Wolynes, Reference Bryngelson and Wolynes1987; Onuchic and Wolynes, Reference Onuchic and Wolynes2004) of the potential energy landscape, quantified via a frustration metric (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017), reveals the persistence of high energy barriers separating low-lying minima. In other words, the frustration reflects the existence of competing configurations. The frustration is caused by different low-lying potential energy minima separated by significant barriers. Here, we find that the landscape is more frustrated for the peptides that contain residues (Y/R) with a higher propensity for phase separation, compared to the residues with a lower phase separation propensity. This observation agrees with the finding that the potential energy landscapes for intrinsically disordered proteins are multi-funnelled (Chebaro et al., Reference Chebaro, Ballard, Chakraborty and Wales2015). However, the frustration metric (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017) alone is not sufficient to predict phase separation propensity. Overall, we observe that the peptides with residues that have high phase separation propensity have distinct peaks or inflection points at low temperatures (significantly below the melting temperature) in
![]() $ {C}_V $
plots and more frustrated potential energy landscapes. These features in
$ {C}_V $
plots and more frustrated potential energy landscapes. These features in
![]() $ {C}_V $
correspond to competing structures stabilised by alternative interactions (aromatic–aromatic or cation–aromatic), or where the residues are oriented differently. This analysis suggests that the calorimetric criterion is a necessary but not a sufficient condition for phase separation (Zhou et al., Reference Zhou, Hall and Karplus1999). The frustration metric provides an additional diagnostic to compare the phase separation propensity of residues in sequences that already exhibit features in
$ {C}_V $
correspond to competing structures stabilised by alternative interactions (aromatic–aromatic or cation–aromatic), or where the residues are oriented differently. This analysis suggests that the calorimetric criterion is a necessary but not a sufficient condition for phase separation (Zhou et al., Reference Zhou, Hall and Karplus1999). The frustration metric provides an additional diagnostic to compare the phase separation propensity of residues in sequences that already exhibit features in
![]() $ {C}_V $
at low temperatures.
$ {C}_V $
at low temperatures.
Methods
The workflow adopted during the current study is presented in Fig. 1 and summarised below. The peptide sequences are constructed using the stickers-and-spacers model (Holehouse and Pappu, Reference Holehouse and Pappu2018b), and the hexapeptides are modelled using the FF99IDPs (Case et al., Reference Case, Cheatham, Darden, Gohlke, Luo, Merz, Onufriev, Simmerling, Wang and Woods2005; Wang et al., Reference Wang, Ye, Jiang, Luo and Chen2014) force field (Step 1, Fig. 1). The FF19SB (Tian et al., Reference Tian, Kasavajhala, Belfon, Raguette, Huang, Migues, Bickel, Wang, Pincay, Wu and Simmerling2020) potential was also tested for some of the peptides to ensure that the structures represented by
![]() $ {C}_V $
features depend on the interactions within the sequence and not on the force field (Supplementary Material). The potential energy landscape is then explored using basin-hopping parallel tempering (BHPT; Step 2, Fig. 1) (Li and Scheraga, Reference Li and Scheraga1987, Reference Li and Scheraga1988; Wales and Doye, Reference Wales and Doye1997; Strodel et al., Reference Strodel, Lee, Whittleston and Wales2010). Discrete path sampling (Wales, Reference Wales2002) is employed to find the connected pathways between local minima (Step 3, Fig. 1). The convergence of sampling is monitored via disconnectivity graphs (Becker and Karplus, Reference Becker and Karplus1997; Wales et al., Reference Wales, Miller and Walsh1998) and heat capacities. The
$ {C}_V $
features depend on the interactions within the sequence and not on the force field (Supplementary Material). The potential energy landscape is then explored using basin-hopping parallel tempering (BHPT; Step 2, Fig. 1) (Li and Scheraga, Reference Li and Scheraga1987, Reference Li and Scheraga1988; Wales and Doye, Reference Wales and Doye1997; Strodel et al., Reference Strodel, Lee, Whittleston and Wales2010). Discrete path sampling (Wales, Reference Wales2002) is employed to find the connected pathways between local minima (Step 3, Fig. 1). The convergence of sampling is monitored via disconnectivity graphs (Becker and Karplus, Reference Becker and Karplus1997; Wales et al., Reference Wales, Miller and Walsh1998) and heat capacities. The
![]() $ {C}_V $
analysis is performed using the harmonic superposition approximation (Step 4, Fig. 1) (Wales, Reference Wales2017), and the frustration in the landscape is quantified via a frustration metric (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017).
$ {C}_V $
analysis is performed using the harmonic superposition approximation (Step 4, Fig. 1) (Wales, Reference Wales2017), and the frustration in the landscape is quantified via a frustration metric (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017).

Figure 1. Schematic figure representing the workflow for the computational potential energy landscape exploration to interrogate peptides of varying phase separation propensities.
Peptide model using AMBER
The hexapeptides are modelled using a properly symmetrised (Malolepsza et al., Reference Malolepsza, Strodel, Khalili, Trygubenko, Fejer and Wales2010) version of the FF99IDPs (Wang et al., Reference Wang, Ye, Jiang, Luo and Chen2014) force field along with an implicit solvent model (igb = 8), and a monovalent ion concentration of 0.1 M (Case et al., Reference Case, Cheatham, Darden, Gohlke, Luo, Merz, Onufriev, Simmerling, Wang and Woods2005, Reference Case, Duke, Walker, Skrynnikov, Cheatham, Mikhailovskii, Simmerling, Xue, Roitberg and Izmailov2022). The N- and C-terminals are methylated and methylamidated, respectively, to cap the charges in the zwitterionic form of the peptide (Step 1, Fig. 1). We also tested another force field, FF19SB (Tian et al., Reference Tian, Kasavajhala, Belfon, Raguette, Huang, Migues, Bickel, Wang, Pincay, Wu and Simmerling2020), and the uncapped peptides for both the force fields. The corresponding results are presented in the Supplementary Material.
Basin-hopping parallel tempering
The global optimisation program GMIN (Wales, Reference Wales2023a) is used to perform basin-hopping (Wales and Doye, Reference Wales and Doye1997; Strodel et al., Reference Strodel, Lee, Whittleston and Wales2010; Li and Scheraga, Reference Li and Scheraga1987, Reference Li and Scheraga1988). For the current computation, the AMBER interface with GMIN is employed. A total of 16 replicas are used with temperatures exponentially distributed between 300 and 575 K. The exchanges are attempted at random with a mean frequency of 10, that is, an average of one exchange every 10 steps. The potential energy landscape is explored by performing 100,000 Cartesian coordinate steps and group rotation (Mochizuki et al., Reference Mochizuki, Whittleston, Somani, Kusumaatmaja and Wales2014) moves for the side chains. The local minima with C
![]() $ {}_{\alpha } $
in D-form and peptide bonds as cis-isomer are discarded. A root-mean-square (RMS) force convergence criterion of 10
$ {}_{\alpha } $
in D-form and peptide bonds as cis-isomer are discarded. A root-mean-square (RMS) force convergence criterion of 10
![]() $ {}^{-7} $
kcal/(mol Angstrom) is employed to save the 400 lowest energy structures differing by at least 0.01 kcal mol
$ {}^{-7} $
kcal/(mol Angstrom) is employed to save the 400 lowest energy structures differing by at least 0.01 kcal mol
![]() $ {}^{-1} $
(to ensure uniqueness of local minima) after running BHPT (Step 2, Fig. 1) (Strodel et al., Reference Strodel, Lee, Whittleston and Wales2010).
$ {}^{-1} $
(to ensure uniqueness of local minima) after running BHPT (Step 2, Fig. 1) (Strodel et al., Reference Strodel, Lee, Whittleston and Wales2010).
Discrete path sampling
Discrete path sampling (Wales, Reference Wales2002) implemented in the OPTIM (Wales, Reference Wales2023b) and PATHSAMPLE (Wales, Reference Wales2023c) programs is used to find optimal pathways between the local minima and the global minimum. A discrete path is defined as an elementary rearrangement between a local minimum, transition state, and another local minimum. The local minimum is defined as a stationary point with no negative Hessian eigenvalues, whereas a transition state is a first-order saddle point with exactly one negative Hessian eigenvalue (Murrell and Laidler, Reference Murrell and Laidler1968; Wales, Reference Wales2003). The doubly-nudged (Trygubenko and Wales, Reference Trygubenko and Wales2004) elastic-band algorithm (Henkelman and Jónsson, Reference Henkelman and Jónsson2000; Henkelman et al., Reference Henkelman, Uberuaga and Jónsson2000) is used to generate candidate transition states, which are then refined accurately using hybrid eigenvector-following (Munro and Wales, Reference Munro and Wales1999). Approximate steepest-descent is employed to find the local minima connected by the transition state using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm (Nocedal, Reference Nocedal1980; Liu and Nocedal, Reference Liu and Nocedal1989). Dijkstra’s shortest path algorithm (Dijkstra, Reference Dijkstra1959) is then used to choose the next pair of minima for which a new connection attempt is made, and the process is repeated until a fully connected pathway is found between the minima of interest using the missing connection algorithm (Carr et al., Reference Carr, Trygubenko and Wales2005). In the case of some peptides, chain crossing is observed. For these peptides, quasi-continuous interpolation (QCI) (Wales and Carr, Reference Wales and Carr2012; Röder and Wales, Reference Röder and Wales2018) is employed to find the correct pathways. Finally, the stationary point database is optimised using the UNTRAP procedure (Strodel et al., Reference Strodel, Whittleston and Wales2007) in PATHSAMPLE to remove artificial frustration in the landscape; that is, low-lying minima separated by large barriers where a lower energy transition state exists. The convergence of the stationary point database is monitored by the convergence of low-temperature peaks in
![]() $ {C}_V $
plots, and by analysing the disconnectivity graph (Step 3, Fig. 1).
$ {C}_V $
plots, and by analysing the disconnectivity graph (Step 3, Fig. 1).
Disconnectivity graphs
The potential energy landscape of a system of
![]() $ N $
atoms lies in a (
$ N $
atoms lies in a (
![]() $ 3N+1 $
)-dimensional space. Disconnectivity graphs provide a powerful way to visualise the multi-dimensional potential energy landscape (Becker and Karplus, Reference Becker and Karplus1997; Wales et al., Reference Wales, Miller and Walsh1998). They preserve the information about the minimum barrier for transitions between minima. The vertical axis of the disconnectivity graph represents the potential (or free) energy. The nodes on the vertical axis represent superbasins composed of disjoint sets of minima. Minima lying within the same superbasin can interconvert via a barrier less than or equal to the energy represented by the superbasin. Each branch originates from a node representing the superbasin and terminates at the energy of a local minimum corresponding to a single branch (Step 3, Fig. 1).
$ 3N+1 $
)-dimensional space. Disconnectivity graphs provide a powerful way to visualise the multi-dimensional potential energy landscape (Becker and Karplus, Reference Becker and Karplus1997; Wales et al., Reference Wales, Miller and Walsh1998). They preserve the information about the minimum barrier for transitions between minima. The vertical axis of the disconnectivity graph represents the potential (or free) energy. The nodes on the vertical axis represent superbasins composed of disjoint sets of minima. Minima lying within the same superbasin can interconvert via a barrier less than or equal to the energy represented by the superbasin. Each branch originates from a node representing the superbasin and terminates at the energy of a local minimum corresponding to a single branch (Step 3, Fig. 1).
Heat capacity analysis
The harmonic superposition approximation (which is accurate at low temperatures) can be used to express the total partition function as a sum of partition functions of all the local minima. The individual partition functions for the local minima are obtained using normal mode analysis, which yields the harmonic approximation to the vibrational density of states.
![]() $ {C}_V $
can now be expressed in terms of occupation probabilities of local minima and their temperature derivatives (Wales, Reference Wales2017), that is,
$ {C}_V $
can now be expressed in terms of occupation probabilities of local minima and their temperature derivatives (Wales, Reference Wales2017), that is,
 $$ {\displaystyle \begin{array}{c}{C}_V=\kappa {k}_B+{k}_B{T}^2\sum \limits_{\alpha}\hskip0.35em {g}_{\alpha }(T)\left(\frac{\partial \ln {p}_{\alpha }(T)}{\partial T}\right)\\ {}=\kappa {k}_B+\sum \limits_{\alpha}^{g_{\alpha }(T)<0}{g}_{\alpha }(T)\left({V}_{\alpha }-{\left\langle V\right\rangle}_{min}\right)+\sum \limits_{\alpha}^{g_{\alpha }(T)>0}{g}_{\alpha }(T)\left({V}_{\alpha }-{\left\langle V\right\rangle}_{min}\right)\\ {}\equiv \kappa {k}_B+{C}^{-}(T)+{C}^{+}(T).\end{array}} $$
$$ {\displaystyle \begin{array}{c}{C}_V=\kappa {k}_B+{k}_B{T}^2\sum \limits_{\alpha}\hskip0.35em {g}_{\alpha }(T)\left(\frac{\partial \ln {p}_{\alpha }(T)}{\partial T}\right)\\ {}=\kappa {k}_B+\sum \limits_{\alpha}^{g_{\alpha }(T)<0}{g}_{\alpha }(T)\left({V}_{\alpha }-{\left\langle V\right\rangle}_{min}\right)+\sum \limits_{\alpha}^{g_{\alpha }(T)>0}{g}_{\alpha }(T)\left({V}_{\alpha }-{\left\langle V\right\rangle}_{min}\right)\\ {}\equiv \kappa {k}_B+{C}^{-}(T)+{C}^{+}(T).\end{array}} $$
Here,
![]() $ {C}_V $
is the heat capacity,
$ {C}_V $
is the heat capacity,
![]() $ \kappa =3N-6 $
is the number of vibrational degrees of freedom for a system of
$ \kappa =3N-6 $
is the number of vibrational degrees of freedom for a system of
![]() $ N $
atoms,
$ N $
atoms,
![]() $ {k}_B $
is the Boltzmann constant,
$ {k}_B $
is the Boltzmann constant,
![]() $ {g}_{\alpha }(T)\equiv \partial {p}_{\alpha }(T)/\partial T $
is the derivative of the occupation probability
$ {g}_{\alpha }(T)\equiv \partial {p}_{\alpha }(T)/\partial T $
is the derivative of the occupation probability
![]() $ {p}_{\alpha } $
for minimum
$ {p}_{\alpha } $
for minimum
![]() $ \alpha $
with respect to temperature
$ \alpha $
with respect to temperature
![]() $ T $
,
$ T $
,
![]() $ {V}_{\alpha } $
is the potential energy of minimum
$ {V}_{\alpha } $
is the potential energy of minimum
![]() $ \alpha $
, and
$ \alpha $
, and
![]() $ {\left\langle V\right\rangle}_{min} $
is the mean potential energy of the minima. The peaks in
$ {\left\langle V\right\rangle}_{min} $
is the mean potential energy of the minima. The peaks in
![]() $ {C}_V $
represent transitions between states with decreasing (
$ {C}_V $
represent transitions between states with decreasing (
![]() $ {g}_{\alpha }(T)<0 $
) and increasing (
$ {g}_{\alpha }(T)<0 $
) and increasing (
![]() $ {g}_{\alpha }(T)>0 $
) occupation probability (Wales, Reference Wales2017).
$ {g}_{\alpha }(T)>0 $
) occupation probability (Wales, Reference Wales2017).
Frustration metric calculation
Competing low-energy minima separated by significant barriers make the potential energy landscape frustrated. The frustration of the potential energy landscape can be quantified using a frustration metric (
![]() $ \tilde{f}(T) $
), which is a function of temperature:
$ \tilde{f}(T) $
), which is a function of temperature:
 $$ \tilde{f}(T)=\sum \limits_{\alpha \ne gmin}\frac{p_{\alpha}^{eq}(T)}{1-{p}_{gmin}^{eq}(T)}\left(\frac{V_{\alpha}^{\dagger }-{V}_{gmin}}{V_{\alpha }-{V}_{gmin}}\right). $$
$$ \tilde{f}(T)=\sum \limits_{\alpha \ne gmin}\frac{p_{\alpha}^{eq}(T)}{1-{p}_{gmin}^{eq}(T)}\left(\frac{V_{\alpha}^{\dagger }-{V}_{gmin}}{V_{\alpha }-{V}_{gmin}}\right). $$
Here,
![]() $ \tilde{f}(T) $
is the frustration metric at temperature
$ \tilde{f}(T) $
is the frustration metric at temperature
![]() $ T $
,
$ T $
,
![]() $ {V}_{gmin} $
is the potential energy of the global minimum in the database,
$ {V}_{gmin} $
is the potential energy of the global minimum in the database,
![]() $ {V}_{\alpha } $
is the potential energy of minimum
$ {V}_{\alpha } $
is the potential energy of minimum
![]() $ \alpha $
,
$ \alpha $
,
![]() $ {V}_{\alpha}^{\dagger } $
is the potential energy of the highest energy transition state on the lowest energy pathway between
$ {V}_{\alpha}^{\dagger } $
is the potential energy of the highest energy transition state on the lowest energy pathway between
![]() $ \alpha $
and the global minimum, and
$ \alpha $
and the global minimum, and
![]() $ {p}_{\alpha}^{eq} $
and
$ {p}_{\alpha}^{eq} $
and
![]() $ {p}_{gmin}^{eq} $
are the equilibrium occupation probabilities of minimum
$ {p}_{gmin}^{eq} $
are the equilibrium occupation probabilities of minimum
![]() $ \alpha $
and the global minimum, which are calculated using the harmonic vibrational density of states. The global minimum does not contribute to frustration and its inclusion leads to an erroneous decrease in frustration at low temperature. Hence, the global minimum is excluded from the frustration metric calculation and occupation probabilities of the remaining minima are renormalised (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017).
$ \alpha $
and the global minimum, which are calculated using the harmonic vibrational density of states. The global minimum does not contribute to frustration and its inclusion leads to an erroneous decrease in frustration at low temperature. Hence, the global minimum is excluded from the frustration metric calculation and occupation probabilities of the remaining minima are renormalised (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017).
Results and discussion
The importance of multivalency (Li et al., Reference Li, Banjade, Cheng, Kim, Chen, Guo, Llaguno, Hollingsworth, King, Banani, Russo, Jiang, Nixon and Rosen2012), interaction strength (Asherie et al., Reference Asherie, Lomakin and Benedek1996; Das and Pappu, Reference Das and Pappu2013; Hyman et al., Reference Hyman, Weber and Jülicher2014; Brangwynne et al., Reference Brangwynne, Tompa and Pappu2015; Choi et al., Reference Choi, Holehouse and Pappu2020), and accessibility (Ruff et al., Reference Ruff, Choi, Cox, Ormsby, Myung, Ascher, Radford, Pappu and Hatters2022) of stickers in promoting phase separation is well established. Here, we explore the energy landscapes (Fig. 2) of various hexapeptides containing a pair of dipeptide stickers separated by a GG spacer. The dipeptide stickers include FF, YY, RY, KY, YR, YK, RE, KE, FL, LF, and LL (Abbas et al., Reference Abbas, Lipiński, Nakashima, Huck and Spruijt2021). These sequences are chosen to encode the aromatic–aromatic, cation–aromatic, cation–anion and CH–
![]() $ \pi $
interactions. The interactions between individual pairs of amino acids are further interrogated by analysing hexapeptides with a pair of stickers separated by two or four glycines. Energy landscapes are also explored for poly-amino acid hexapeptides containing a single type of amino acid residue, including alanine (A), glycine (G), valine (V), arginine (R) and lysine (K). The peptides containing residues with better phase separation propensity show clear features in
$ \pi $
interactions. The interactions between individual pairs of amino acids are further interrogated by analysing hexapeptides with a pair of stickers separated by two or four glycines. Energy landscapes are also explored for poly-amino acid hexapeptides containing a single type of amino acid residue, including alanine (A), glycine (G), valine (V), arginine (R) and lysine (K). The peptides containing residues with better phase separation propensity show clear features in
![]() $ {C}_V $
at low temperatures (Fig. 3a, see section “Heat capacity at low temperature”). These features are caused by competing low-energy conformations with different types of interactions (Figs 4 and 5, see section “Interactions leading to features in
$ {C}_V $
at low temperatures (Fig. 3a, see section “Heat capacity at low temperature”). These features are caused by competing low-energy conformations with different types of interactions (Figs 4 and 5, see section “Interactions leading to features in
![]() $ {C}_V $
”). Further analysis of frustration reveals that the peptides with amino acids encoding better phase separation propensity result in more frustrated landscapes (Fig. 3b, see section “Frustration in the energy landscape”). It is hypothesised that the collective behaviour of phase separation may be understood in terms of single-molecule properties by quantifying the heat capacity and frustration within the energy landscape framework. An interesting analogue is how the existence of different conformations leads to polymorphic forms for various organic and inorganic molecules (Supplementary Material). A recent study has also shown links between heat capacity change during unfolding and multicomponent phase separation behaviour (Rana et al., Reference Rana, Kodirov, Shakya and King2023).
$ {C}_V $
”). Further analysis of frustration reveals that the peptides with amino acids encoding better phase separation propensity result in more frustrated landscapes (Fig. 3b, see section “Frustration in the energy landscape”). It is hypothesised that the collective behaviour of phase separation may be understood in terms of single-molecule properties by quantifying the heat capacity and frustration within the energy landscape framework. An interesting analogue is how the existence of different conformations leads to polymorphic forms for various organic and inorganic molecules (Supplementary Material). A recent study has also shown links between heat capacity change during unfolding and multicomponent phase separation behaviour (Rana et al., Reference Rana, Kodirov, Shakya and King2023).

Figure 2. Representative disconnectivity graphs (Becker and Karplus, Reference Becker and Karplus1997; Wales et al., Reference Wales, Miller and Walsh1998) for some of the peptides studied. The scale bar is 1 kcal mol
![]() $ {}^{-1} $
.
$ {}^{-1} $
.
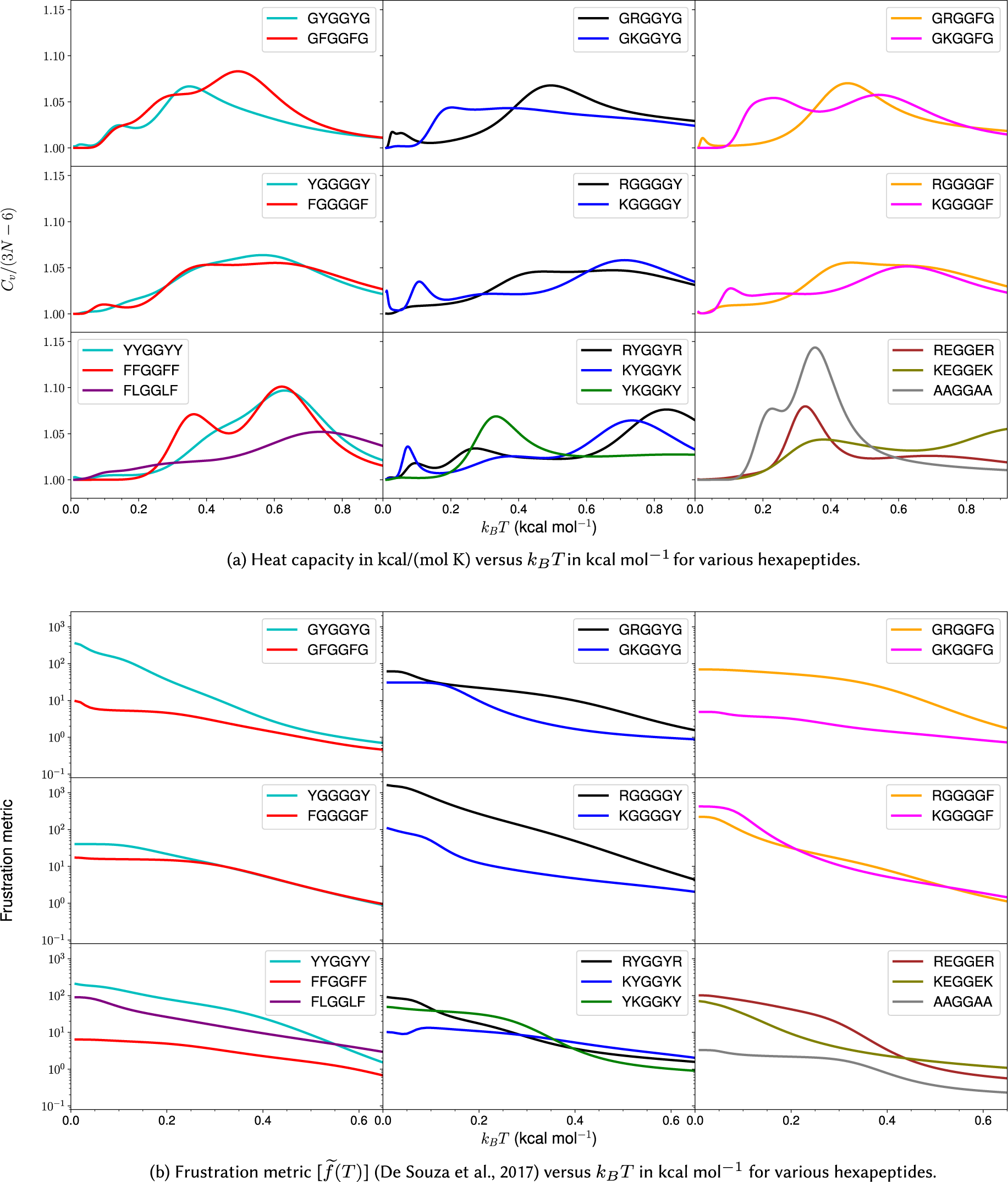
Figure 3. Heat capacity and frustration metric diagnostic for probing phase separation propensity encoded by different amino acid residues.
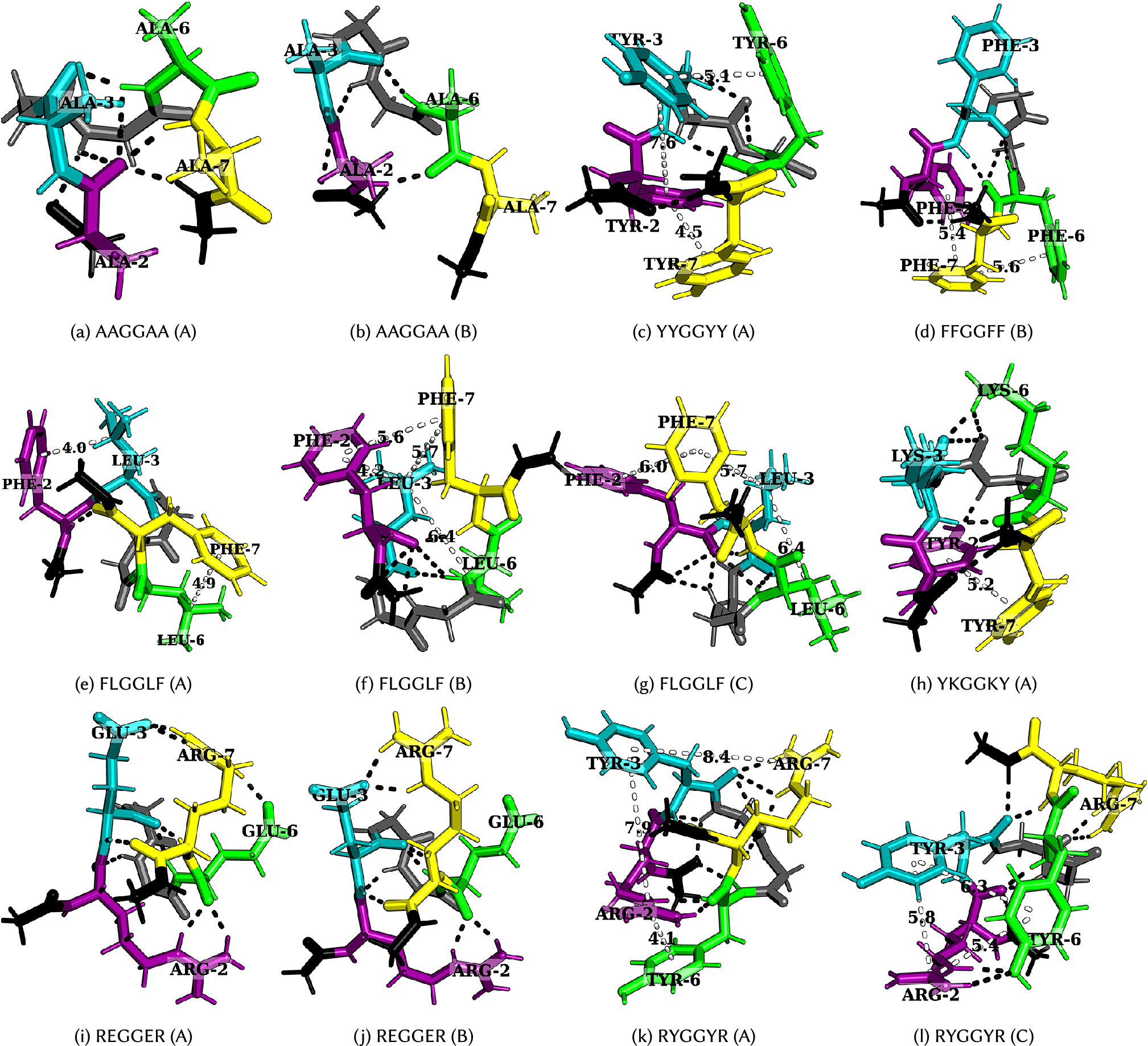
Figure 4. Structures corresponding to low-temperature heat capacity features. The first and second peaks correspond to the transition from A to B and then from B to C, respectively.

Figure 5. Structures corresponding to low-temperature heat capacity features. The first and second peaks correspond to the transition from A to B and then from B to C, respectively.
Heat capacity at low temperature
We first investigate the geometric and energetic parameters that underlie the structural differences represented by low-temperature peaks in the heat capacity of peptides with varying phase separation propensities (Fig. 3a). We emphasise that we are using these features as a diagnostic for competing structures in the energy landscape, which may correlate with phase separation propensity. This computational construction does not need to be an accurate calculation of
![]() $ {C}_V $
, nor does it need to be experimentally accessible. These peaks represent the transition between competing structures that have significant enthalpic and entropic differences and the integral over the peak represents the latent heat for this transition. In some
$ {C}_V $
, nor does it need to be experimentally accessible. These peaks represent the transition between competing structures that have significant enthalpic and entropic differences and the integral over the peak represents the latent heat for this transition. In some
![]() $ {C}_V $
plots, instead of distinct peaks, we observe inflection points (GFGGFG, YGGGGY, RGGGGY, RGGGGF, YYGGYY, and FLGGLF) where the curvature of the plot changes. These inflection points (or shoulders) may be caused by overlapping peaks. The temperatures corresponding to these distinct inflection points are also considered, since they may contain useful information. The hexapeptide AAGGAA is taken as the control, as it is predicted to have the lowest phase separation propensity of the set (Wang et al., Reference Wang, Choi, Holehouse, Lee, Zhang, Jahnel, Maharana, Lemaitre, Pozniakovsky, Drechsel, Poser, Pappu, Alberti and Hyman2018), and the corresponding
$ {C}_V $
plots, instead of distinct peaks, we observe inflection points (GFGGFG, YGGGGY, RGGGGY, RGGGGF, YYGGYY, and FLGGLF) where the curvature of the plot changes. These inflection points (or shoulders) may be caused by overlapping peaks. The temperatures corresponding to these distinct inflection points are also considered, since they may contain useful information. The hexapeptide AAGGAA is taken as the control, as it is predicted to have the lowest phase separation propensity of the set (Wang et al., Reference Wang, Choi, Holehouse, Lee, Zhang, Jahnel, Maharana, Lemaitre, Pozniakovsky, Drechsel, Poser, Pappu, Alberti and Hyman2018), and the corresponding
![]() $ {C}_V $
is simpler (the potential energy landscape is not frustrated) compared to other peptides with more phase separation promoting residues. Note that it is not the height of the peaks but the existence of features at low temperature (below the melting temperature) that report on the structural heterogeneities in the landscapes, and hence, the phase separation propensities of the constituent residues in a sequence.
$ {C}_V $
is simpler (the potential energy landscape is not frustrated) compared to other peptides with more phase separation promoting residues. Note that it is not the height of the peaks but the existence of features at low temperature (below the melting temperature) that report on the structural heterogeneities in the landscapes, and hence, the phase separation propensities of the constituent residues in a sequence.
Various other hexapeptides, such as GGGGGG, AAAAAA, VVVVVV, EEEEEE, RRRRRR, and KKKKKK, have also been analysed as controls and are found to show simpler
![]() $ {C}_V $
profiles (Supplementary Material). However, distinct polar contacts between the main-chain atoms or between the main-chain and side-chain atoms can produce features in
$ {C}_V $
profiles (Supplementary Material). However, distinct polar contacts between the main-chain atoms or between the main-chain and side-chain atoms can produce features in
![]() $ {C}_V $
(AAGGAA in Fig. 4a,
b).
$ {C}_V $
(AAGGAA in Fig. 4a,
b).
In general, for hexapeptides with interactions that encode a higher propensity for phase separation, we observe more pronounced features (several distinct peaks and inflection points) in
![]() $ {C}_V $
. The frustration metric can then be used as a further diagnostic. The
$ {C}_V $
. The frustration metric can then be used as a further diagnostic. The
![]() $ {C}_V $
plots for various other peptides are given in the Supplementary Material.
$ {C}_V $
plots for various other peptides are given in the Supplementary Material.
Interactions leading to features in
 $ {C}_V $
$ {C}_V $
A low-temperature heat capacity peak often arises from a transition from a compact structure with two sets of dominant interactions between four residues (YYGGYY – Fig. 4c and FLGGLF – Fig. 4e) to another structure with a similar set of interactions, but with residues oriented differently, or a relatively extended structure with two sets of dominant interactions between three residues (FFGGFF – Fig. 4d and FLGGLF – Fig. 4f, g). Depending on the number of stickers in the peptide, the low-temperature peak may also correspond to a transition from two sets of dominant interactions between three residues to a single principal interaction between two residues (KEGGEK and REGGER – Fig. 4i, j). A detailed discussion of the competing structures for various hexapeptides is given below.
Tyrosine versus phenylalanine: The presence of a hydroxyl group in tyrosine not only enhances its hydrogen-bonding ability, but also results in different rotamers, leading to features in
![]() $ {C}_V $
at low temperatures (GYGGYG and YGGGGY). GFGGFG and GYGGYG exhibit inflection points and distinct peaks at low temperatures, respectively. In particular, the low-temperature feature in GFGGFG and FGGGGF corresponds to the transition between a structure with methyl–aromatic and aromatic–aromatic interactions to a structure with an aromatic–aromatic interaction, which further changes to a structure with several polar contacts between distinct atoms. In contrast, for GYGGYG and YGGGGY, the features at low temperature correspond to the transition between rotamers of the aromatic ring containing methyl–aromatic and aromatic–aromatic interactions. Here, the methyl group belongs to the C-terminal cap of the peptide. Interestingly, the observation of a low-temperature peak resulting from the presence of ring rotamers can be compared to an experimental observation in which a bulge in the
$ {C}_V $
at low temperatures (GYGGYG and YGGGGY). GFGGFG and GYGGYG exhibit inflection points and distinct peaks at low temperatures, respectively. In particular, the low-temperature feature in GFGGFG and FGGGGF corresponds to the transition between a structure with methyl–aromatic and aromatic–aromatic interactions to a structure with an aromatic–aromatic interaction, which further changes to a structure with several polar contacts between distinct atoms. In contrast, for GYGGYG and YGGGGY, the features at low temperature correspond to the transition between rotamers of the aromatic ring containing methyl–aromatic and aromatic–aromatic interactions. Here, the methyl group belongs to the C-terminal cap of the peptide. Interestingly, the observation of a low-temperature peak resulting from the presence of ring rotamers can be compared to an experimental observation in which a bulge in the
![]() $ {C}_V $
plot of polystyrene was attributed to the rotation of the phenyl ring around the chain axis (Warfield and Petree, Reference Warfield and Petree1962). The orientation that optimises the aromatic interaction depends on the distance between the C
$ {C}_V $
plot of polystyrene was attributed to the rotation of the phenyl ring around the chain axis (Warfield and Petree, Reference Warfield and Petree1962). The orientation that optimises the aromatic interaction depends on the distance between the C
![]() $ {}_{\alpha } $
atoms, stacked at a short distance and T-shaped at a longer distance (Hunter et al., Reference Hunter, Singh and Thornton1991; Chelli et al., Reference Chelli, Gervasio, Procacci and Schettino2002). Offset-stacked structures can also be energetically favourable (Ninković et al., Reference Ninković, Andrić, Malkov and Zarić2014), and the methyl group of the cap can also interact with an aromatic residue (Zanuy et al., Reference Zanuy, Haspel, Tsai, Ma, Gunasekaran, Wolfson and Nussinov2004). We observe similar edge-to-face, CH–
$ {}_{\alpha } $
atoms, stacked at a short distance and T-shaped at a longer distance (Hunter et al., Reference Hunter, Singh and Thornton1991; Chelli et al., Reference Chelli, Gervasio, Procacci and Schettino2002). Offset-stacked structures can also be energetically favourable (Ninković et al., Reference Ninković, Andrić, Malkov and Zarić2014), and the methyl group of the cap can also interact with an aromatic residue (Zanuy et al., Reference Zanuy, Haspel, Tsai, Ma, Gunasekaran, Wolfson and Nussinov2004). We observe similar edge-to-face, CH–
![]() $ \pi $
, and methyl–aromatic interactions for GFGGFG (Fig. 5a,
b), GYGGYG (Fig. 5c–e), FGGGGF, and YGGGGY.
$ \pi $
, and methyl–aromatic interactions for GFGGFG (Fig. 5a,
b), GYGGYG (Fig. 5c–e), FGGGGF, and YGGGGY.
Arginine versus lysine: GRGGYG exhibits features in
![]() $ {C}_V $
because of the interaction between R and Y, and the presence of ring rotamers (rotamer of an aromatic ring) for Y (Fig. 5f–h), whereas for GKGGYG and GKGGFG, it is the methyl group in the C-terminal cap that preferably interacts with the Y/F (Fig. 5i,
j). We still see features in
$ {C}_V $
because of the interaction between R and Y, and the presence of ring rotamers (rotamer of an aromatic ring) for Y (Fig. 5f–h), whereas for GKGGYG and GKGGFG, it is the methyl group in the C-terminal cap that preferably interacts with the Y/F (Fig. 5i,
j). We still see features in
![]() $ {C}_V $
for GKGGYG because of ring rotamers for Y. In the case of RYGGYR, one of the peaks corresponds to the structural transition between the aromatic–cation–aromatic interaction motif to the aromatic–cation interaction motif (Fig. 4k,
l). Hence, R has more propensity than K to interact with the aromatic residues.
$ {C}_V $
for GKGGYG because of ring rotamers for Y. In the case of RYGGYR, one of the peaks corresponds to the structural transition between the aromatic–cation–aromatic interaction motif to the aromatic–cation interaction motif (Fig. 4k,
l). Hence, R has more propensity than K to interact with the aromatic residues.
Context-dependence: Phase separation may be regarded as a percolation network transition (Mittag and Pappu, Reference Mittag and Pappu2022). In other words, the formation of a stable condensate occurs when biomolecules interconnect with one another forming a percolated network; the denser the connectivity of the percolated network, the higher the stability of the condensates (Espinosa et al., Reference Espinosa, Joseph, Sanchez-Burgos, Garaizar, Frenkel and Collepardo-Guevara2020). The difference in size, the steric packing of R and K, the number of spacers between the stickers, and the distance between the stickers may be useful in explaining the context-dependent properties of these amino acid residues in terms of accessibility and networking ability of stickers to interact with each other. Consider the peptides RYGGYR, GRGGYG, GKGGYG, RGGGGY, and KGGGGY. Even though the presence of R leads to more features in the
![]() $ {C}_V $
plots, we observe that when the cationic and aromatic residues are far apart, as for RGGGGY and KGGGGY, K seems to be more flexible and less sterically inhibited, and therefore, it can interact well with Y, whereas R seems to be more rigid and does not interact favourably with Y/F (Fig. 5k,
l). Previous reports suggest that K/RNA coacervates are more dynamic than R/RNA coacervates (Ukmar-Godec et al., Reference Ukmar-Godec, Hutten, Grieshop, Rezaei-Ghaleh, Cima-Omori, Biernat, Mandelkow, Soding, Dormann and Zweckstetter2019), and the R-rich motif may act as a phase disruptor (Odeh and Shorter, Reference Odeh and Shorter2020). While the different behaviours of R and K may be understood in terms of the relative strength of the interactions, it is also possible that the flexible nature of K compared to R may play a role. Furthermore, the shuffling of sequence may alter the presence of charged residues near the N-/C-termini, which may lead to differences in the properties of these peptides because of the charge interaction with the peptide dipole. The dipole moment effect is expected to be more significant in the case of an uncapped peptide in zwitterionic form (Marqusee and Baldwin, Reference Marqusee and Baldwin1987; Tkatchenko et al., Reference Tkatchenko, Rossi, Blum, Ireta and Scheffler2011).
$ {C}_V $
plots, we observe that when the cationic and aromatic residues are far apart, as for RGGGGY and KGGGGY, K seems to be more flexible and less sterically inhibited, and therefore, it can interact well with Y, whereas R seems to be more rigid and does not interact favourably with Y/F (Fig. 5k,
l). Previous reports suggest that K/RNA coacervates are more dynamic than R/RNA coacervates (Ukmar-Godec et al., Reference Ukmar-Godec, Hutten, Grieshop, Rezaei-Ghaleh, Cima-Omori, Biernat, Mandelkow, Soding, Dormann and Zweckstetter2019), and the R-rich motif may act as a phase disruptor (Odeh and Shorter, Reference Odeh and Shorter2020). While the different behaviours of R and K may be understood in terms of the relative strength of the interactions, it is also possible that the flexible nature of K compared to R may play a role. Furthermore, the shuffling of sequence may alter the presence of charged residues near the N-/C-termini, which may lead to differences in the properties of these peptides because of the charge interaction with the peptide dipole. The dipole moment effect is expected to be more significant in the case of an uncapped peptide in zwitterionic form (Marqusee and Baldwin, Reference Marqusee and Baldwin1987; Tkatchenko et al., Reference Tkatchenko, Rossi, Blum, Ireta and Scheffler2011).
Aromatic–aromatic versus cation–aromatic interactions: Favourable cation–aromatic interactions between R and Y are observed in RYGGYR (Fig. 4k, l). However for YKGGKY, the aromatic–aromatic interaction between two tyrosine residues is preferred over the cation–aromatic interaction between K and Y (Fig. 4h). This observation hints at the role played by the proximity of interacting residues in a sequence, that is, the two tyrosine residues located at the ends can establish an aromatic–aromatic interaction, which is preferred over the weaker interaction offered by the lysine residues. From a broader perspective, this result may be useful in understanding the context-dependent properties of amino acid residues across different sequences.
Cation–anion interaction: Hydrogen-bonding between oppositely charged amino acids may lead to the formation of salt bridges where the same residue interacts with two different residues (complex) or between two oppositely charged residues (simple) (Musafia et al., Reference Musafia, Buchner and Arad1995). Both REGGER (Fig. 4i,
j) and KEGGEK exhibit low-temperature
![]() $ {C}_V $
peaks corresponding to the transition from structures containing a complex salt bridge to a simple salt bridge. The complex salt bridge is formed by the interaction of the same cationic residue with two anionic residues. The next
$ {C}_V $
peaks corresponding to the transition from structures containing a complex salt bridge to a simple salt bridge. The complex salt bridge is formed by the interaction of the same cationic residue with two anionic residues. The next
![]() $ {C}_V $
peak at a higher temperature corresponds to the transition from a structure with a cation interacting with a particular anion to a structure with the same cation interacting with a different anion in a different orientation, as in the case of uncapped KEGGEK peptide.
$ {C}_V $
peak at a higher temperature corresponds to the transition from a structure with a cation interacting with a particular anion to a structure with the same cation interacting with a different anion in a different orientation, as in the case of uncapped KEGGEK peptide.
Partial phase separation: Leucine and phenylalanine are constituents of peptides exhibiting partial phase separation (Abbas et al., Reference Abbas, Lipiński, Nakashima, Huck and Spruijt2021), and the
![]() $ {C}_V $
plot for FLGGLF contains features at low temperatures. The peak represents the transition from a structure containing two distinct pairs of L–F interactions, arising from four residues, to a structure with two pairs of interactions arising from three residues F, F, and L (Fig. 4e–g). Several CH–
$ {C}_V $
plot for FLGGLF contains features at low temperatures. The peak represents the transition from a structure containing two distinct pairs of L–F interactions, arising from four residues, to a structure with two pairs of interactions arising from three residues F, F, and L (Fig. 4e–g). Several CH–
![]() $ \pi $
interactions can occur between L and F. Hence, partial phase separation may occur for peptides containing amino acids capable of exhibiting distinct pairs of interactions. However, the interaction strength between stickers is weaker compared to the cation/aromatic–aromatic interaction. Although weak, the CH–
$ \pi $
interactions can occur between L and F. Hence, partial phase separation may occur for peptides containing amino acids capable of exhibiting distinct pairs of interactions. However, the interaction strength between stickers is weaker compared to the cation/aromatic–aromatic interaction. Although weak, the CH–
![]() $ \pi $
interaction is known to play an important role in supramolecular organisation (Piccolo, Reference Piccolo2001).
$ \pi $
interaction is known to play an important role in supramolecular organisation (Piccolo, Reference Piccolo2001).
Frustration in the energy landscape
The frustration (Bryngelson and Wolynes, Reference Bryngelson and Wolynes1987; Onuchic and Wolynes, Reference Onuchic and Wolynes2004) in the multi-dimensional potential energy landscape can be visualised by analysing the multiple funnels in the disconnectivity graph representation (Becker and Karplus, Reference Becker and Karplus1997; Wales et al., Reference Wales, Miller and Walsh1998) (Fig. 2). More funnels with low-energy minima separated by significant barriers from the global minimum make the landscape more frustrated at low temperatures. The frustration is high at very low temperatures because the molecules do not have enough thermal energy to overcome the barrier required for transition from one low-energy conformation to another. In other words, if the state of system corresponds to a low-energy minimum in one funnel, the system is likely to remain in the same funnel when the frustration is high. At higher temperatures the thermal energy is larger and so the molecules have sufficient energy to overcome the barriers and transition between local minima. Hence, the system is less frustrated at higher temperatures. Quantitatively, the frustration metric (De Souza et al., Reference De Souza, Stevenson, Niblett, Farrell and Wales2017) is generally larger for peptides containing Y/R than for peptides containing F/K at lower temperatures (Fig. 3b). In particular, at a very low temperature corresponding to
![]() $ {k}_BT= $
0.2 kcal mol
$ {k}_BT= $
0.2 kcal mol
![]() $ {}^{-1} $
, the frustration metric for GYGGYG is 8 times the value for GFGGFG, YYGGYY is 16 times larger than FFGGFF, GRGGYG is 2 times larger than GKGGYG, GRGGFG is 16 times larger than GKGGFG, and REGGER is 5 times larger than KEGGEK. At
$ {}^{-1} $
, the frustration metric for GYGGYG is 8 times the value for GFGGFG, YYGGYY is 16 times larger than FFGGFF, GRGGYG is 2 times larger than GKGGYG, GRGGFG is 16 times larger than GKGGFG, and REGGER is 5 times larger than KEGGEK. At
![]() $ {k}_BT= $
0.1 kcal mol
$ {k}_BT= $
0.1 kcal mol
![]() $ {}^{-1} $
the frustration metric of RYGGYR is 3 times greater than that of KYGGYK. Hence, it appears that the frustration in the landscape for the monomer peptide directly correlates with the relative phase separation propensity of its constituent residues. This result can also be rationalised by correlating the high frustration with the tendency to be trapped in the unfolded state, and it is well known that unfolded states and intrinsically disordered proteins promote phase separation (Majumdar et al., Reference Majumdar, Dogra, Maity and Mukhopadhyay2019). Interestingly, KGGGGF is three times more frustrated than RGGGGF at very low temperature (
$ {}^{-1} $
the frustration metric of RYGGYR is 3 times greater than that of KYGGYK. Hence, it appears that the frustration in the landscape for the monomer peptide directly correlates with the relative phase separation propensity of its constituent residues. This result can also be rationalised by correlating the high frustration with the tendency to be trapped in the unfolded state, and it is well known that unfolded states and intrinsically disordered proteins promote phase separation (Majumdar et al., Reference Majumdar, Dogra, Maity and Mukhopadhyay2019). Interestingly, KGGGGF is three times more frustrated than RGGGGF at very low temperature (
![]() $ {k}_BT= $
0.1 kcal mol
$ {k}_BT= $
0.1 kcal mol
![]() $ {}^{-1} $
). Here, the larger number of spacers (four glycines) increases the distance between the stickers and affects the inaccessibility. The accessibility is reduced more in the case of R, which appears more rigid compared to the more flexible K residue. This difference may explain the context-dependent properties of R in phase-separating proteins. Moreover, the potential energy landscape of FLGGLF is five times more frustrated than FFGGFF at a very low temperature (
$ {}^{-1} $
). Here, the larger number of spacers (four glycines) increases the distance between the stickers and affects the inaccessibility. The accessibility is reduced more in the case of R, which appears more rigid compared to the more flexible K residue. This difference may explain the context-dependent properties of R in phase-separating proteins. Moreover, the potential energy landscape of FLGGLF is five times more frustrated than FFGGFF at a very low temperature (
![]() $ {k}_BT= $
0.2 kcal mol
$ {k}_BT= $
0.2 kcal mol
![]() $ {}^{-1} $
). However, FFGGFF has distinct peaks in the
$ {}^{-1} $
). However, FFGGFF has distinct peaks in the
![]() $ {C}_V $
, in contrast to FLGGLF (Fig. 3a). These features are caused by a stronger aromatic–aromatic interaction between two F, which correlates with the better phase separation propensity of residues in FFGGFF, whereas the interaction between F and L may facilitate partial phase separation (Abbas et al., Reference Abbas, Lipiński, Nakashima, Huck and Spruijt2021). The frustration metric plots for various other peptides are given in the Supplementary Material.
$ {C}_V $
, in contrast to FLGGLF (Fig. 3a). These features are caused by a stronger aromatic–aromatic interaction between two F, which correlates with the better phase separation propensity of residues in FFGGFF, whereas the interaction between F and L may facilitate partial phase separation (Abbas et al., Reference Abbas, Lipiński, Nakashima, Huck and Spruijt2021). The frustration metric plots for various other peptides are given in the Supplementary Material.
Conclusions
We have investigated the hypothesis that the energy landscape of peptide monomers may report on their phase separation ability, which is a collective phenomenon. The different possible arrangements in which the aromatic–aromatic and cation–aromatic interactions can occur in a peptide monomer can produce low-temperature peaks in the heat capacity. Additionally, the high barriers between the alternative low-lying potential energy minima and the existence of several such conformations, as visualised by multiple funnels in the disconnectivity graph, produce a highly frustrated potential energy landscape. Together, features in the heat capacity plot, and the frustration of the landscape, quantified using the frustration metric, appear to correlate with increased phase separation propensity of the constituent residues. The high frustration results from the molecule being trapped in an intrinsically disordered or unfolded state, and both these states are known to promote phase separation.
This analysis also provides a useful framework to investigate the context-dependent properties of amino acid residues in different sequences. While there have been several attempts (Dzuricky et al., Reference Dzuricky, Rogers, Shahid, Cremer and Chilkoti2020; Simon et al., Reference Simon, Carroll, Rubinstein, Chilkoti and López2017) to guide the rational design of peptides useful for bioengineering applications, the present study presents a new perspective to design peptides with targeted phase separation behaviour. A related study provides links between the secondary structures that contribute to low-temperature
![]() $ {C}_V $
features for monomers and dimers of hexapeptide sequences that are experimentally known to aggregate (Nicy and Wales, Reference Nicy and Wales2023). It is important to understand that we are not actually interested in the low-temperature behaviour of the heat capacity and that an accurate calculation is not required. Rather, we are using peaks in an approximate
$ {C}_V $
features for monomers and dimers of hexapeptide sequences that are experimentally known to aggregate (Nicy and Wales, Reference Nicy and Wales2023). It is important to understand that we are not actually interested in the low-temperature behaviour of the heat capacity and that an accurate calculation is not required. Rather, we are using peaks in an approximate
![]() $ {C}_V $
as a computational construction to diagnose competition between alternative favourable structures. It is the characteristics of these conformations that may provide a structural interpretation and diagnostic of higher-order behaviour in condensates, such as liquid–liquid phase separation. Our results suggest that there may indeed be such a connection. We do not claim that this connection is universal, but we do suggest that it may be useful.
$ {C}_V $
as a computational construction to diagnose competition between alternative favourable structures. It is the characteristics of these conformations that may provide a structural interpretation and diagnostic of higher-order behaviour in condensates, such as liquid–liquid phase separation. Our results suggest that there may indeed be such a connection. We do not claim that this connection is universal, but we do suggest that it may be useful.
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/qrd.2023.5.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/qrd.2023.5.
Data availability statement
The discrete path sampling databases are available at https://doi.org/10.17863/CAM.96972 (Nicy et al., Reference Nicy, Joseph, Collepardo-Guevara and Wales2023). The step-by-step protocol for creating one such database is given as a tutorial on https://github.com/nicy-nicy/peptide-energy-landscape-exploration. The scripts to analyse the databases can be found at https://github.com/nicy-nicy/energy-landscape-cv-analysis.
Author contribution
J.A.J., R.C.G., D.J.W., and Nicy conceived the idea and designed the study. Nicy performed the simulations and wrote the first draft. All the authors helped with the analysis, interpretation of data and corrected the final draft.
Financial support
This work was supported by Engineering and Physical Sciences Research Council (EPSRC) (D.J.W., Grant No. EP/N035003/1), the Cambridge Commonwealth, European and International Trust, the Allen, Meek and Read Fund, the Santander fund, St Edmund’s College, University of Cambridge, and the Trinity-Henry Barlow Honorary Award (Nicy).
Competing interest
The authors declare no competing interest exists.




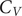
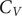
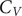







Comments
Comments to Author: I found the physics based approach taken in this paper - e.g. probing the importance of the free energy landscape of short peptides on their phase behaviour - an extremely interesting one. The assumptions (e.g. approximations in the calculation Cv) are robustly discussed and justified in terms of the physics being learned from the study. I found Fig 1 helpful in understanding the simulation methodology. Given that this method would be of interest to a broad range of disciplines, and the importance of membraneless organelles, I would invite the authors to add a few more sentences in specific areas providing readers with a bit more background, so that researchers who are not experts in biological phase separation can enjoy the work.
For example, it would be helpful to briefly explain (e.g. 1/2 sentences) the ideas for why phase separation and intrinsic disorder are related in the introduction.
Please could “the stickers and spacers” model be briefly explained (line 61).
Please could the percolation network model of phase separation be explained (line 269).
I found the Temperature units in Fig 3 rather confusing - would plain Kelvin be clearer to readers? I also wondered why the frustration decreases with temperature, and if the authors might provide a bit more explanation about how this metric is expected to behave. For example, I would have thought that the frustration is zero at 0K when all systems are in their absolute ground state but that doesn’t seem to becorrect. Maybe a couple of toy examples and their high/low temperature limits could be described in the text to help provide the readers with a physical picture of the meaning of the frustration.
The authors are rather cautious and they do not provide any hypothesis as to the thermodynamic mechanisms for why a frustrated free energy landscape would make peptides more likely to phase separate. I would welcome such an addition in the final paragraph, even if the ideas are speculative, or if there are potentially conflicting viewpoints that need to be discussed. Equally, I am aware that this is not considered appropriate in certain areas of soft matter, so I leave it to the authors to judge.