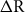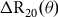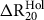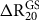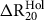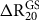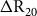1 INTRODUCTION
1.1 Marine 14C Calibration
To aid calibration of radiocarbon (14C) samples from open-ocean surface marine environments, the IntCal working group regularly produce marine radiocarbon age calibration curves (known as MarineXX, where XX denotes the year in which the calibration curve was produced). The most recent marine calibration curve is Marine20 (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020) which has replaced the earlier 1986, 1993, 1998, Marine04, Marine09, and Marine13 curves (Hughen et al. Reference Hughen, Baillie, Bard, Beck, Bertrand, Blackwell, Buck, Burr, Cutler and Damon2004; Reimer et al. Reference Reimer, Baillie, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Burr and Edwards2009, Reference Reimer, Bard, Bayliss, Beck, Blackwell, Bronk Ramsey, Buck, Cheng, Edwards and Friedrich2013; Stuiver et al. Reference Stuiver, Pearson and Braziunas1986, Reference Stuiver, Reimer, Bard, Beck, Burr, Hughen, Kromer, McCormac, van der Plicht and Spurk1998; Stuiver and Braziunas Reference Stuiver and Braziunas1993). The aim of all these marine radiocarbon age calibration curves is to provide a best estimate of the global-scale changes in open ocean surface 14C levels over the past 55,000 years that incorporates the oceanic smoothing of atmospheric 14C-age variations and accounts for large-scale paleoclimatic, paleoceanographic, and carbon cycle changes. To enable consistent calibration of marine 14C samples, the community typically make the significant simplification that any further localized changes in surface ocean depletion are approximately constant over time, and that the global-scale changes modeled within the MarineXX curves capture the main temporal variations in oceanic 14C depletion (Heaton et al. Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022).
In polar regions such a simplification cannot however be justified. At high-latitudes, during glacial periods, we expect there may have been significant additional localized changes in surface-water 14C concentration (Butzin et al. Reference Butzin, Prange and Lohmann2005) that are not captured by the global-scale MarineXX curves. These temporal changes, to what is known as the regional
![]() ${\rm{\Delta }}R\left( \theta \right)$
, make the calibration of marine 14C samples from such polar regions particularly challenging. Without adjustment to account for potential variations over time in polar
${\rm{\Delta }}R\left( \theta \right)$
, make the calibration of marine 14C samples from such polar regions particularly challenging. Without adjustment to account for potential variations over time in polar
![]() ${\rm{\Delta }}R\left( \theta \right)$
, none of the MarineXX curves should be used for calibration of marine 14C samples from polar regions in glacial periods. If we do not account for such temporal changes in
${\rm{\Delta }}R\left( \theta \right)$
, none of the MarineXX curves should be used for calibration of marine 14C samples from polar regions in glacial periods. If we do not account for such temporal changes in
![]() ${\rm{\Delta }}R\left( \theta \right)$
it is likely we will obtain calibrated age estimates for polar 14C samples in glacial periods that are spuriously precise and biased towards being older than their true calendar ages.
${\rm{\Delta }}R\left( \theta \right)$
it is likely we will obtain calibrated age estimates for polar 14C samples in glacial periods that are spuriously precise and biased towards being older than their true calendar ages.
Before the impact of anthropogenic emissions, the concentration of 14C in the surface ocean has always been depleted compared with the level of 14C in the contemporaneous atmosphere. Oceanic 14C levels also show a smoother response to 14C production changes than the atmosphere: variations in 14C-age (and
![]() ${{\rm{\Delta }}^{14}}$
C) over time are damped in the oceans compared to the atmosphere (Levin and Hesshaimer Reference Levin and Hesshaimer2000). We measure the overall surface ocean 14C depletion, at any location and time, via the marine reservoir age (MRA). This MRA, denoted
${{\rm{\Delta }}^{14}}$
C) over time are damped in the oceans compared to the atmosphere (Levin and Hesshaimer Reference Levin and Hesshaimer2000). We measure the overall surface ocean 14C depletion, at any location and time, via the marine reservoir age (MRA). This MRA, denoted
![]() ${R^{Location}}\left( \theta \right)$
, defines the difference, at calendar age
${R^{Location}}\left( \theta \right)$
, defines the difference, at calendar age
![]() $\theta $
cal yr BP, between the radiocarbon age of dissolved inorganic carbon in the mixed ocean surface layer at that location, and the radiocarbon age of CO2 in the Northern Hemispheric (NH) atmosphere (Stuiver et al. Reference Stuiver, Pearson and Braziunas1986).
$\theta $
cal yr BP, between the radiocarbon age of dissolved inorganic carbon in the mixed ocean surface layer at that location, and the radiocarbon age of CO2 in the Northern Hemispheric (NH) atmosphere (Stuiver et al. Reference Stuiver, Pearson and Braziunas1986).
The overall MRA,
![]() ${R^{Location}}\left( \theta \right)$
, in a particular location is influenced by both global-scale factors and local-scale factors (Bard Reference Bard1988; Stuiver and Braziunas Reference Stuiver and Braziunas1993):
${R^{Location}}\left( \theta \right)$
, in a particular location is influenced by both global-scale factors and local-scale factors (Bard Reference Bard1988; Stuiver and Braziunas Reference Stuiver and Braziunas1993):
Here,
![]() ${R^{GlobalAv}}\left( \theta \right)$
captures the global-scale MRA effects; and
${R^{GlobalAv}}\left( \theta \right)$
captures the global-scale MRA effects; and
![]() ${\rm{\Delta }}{R^{Location}}\left( \theta \right)$
the local-scale depletion factors. Global-scale factors include atmospheric CO2 (Köhler et al. Reference Köhler, Nehrbass-Ahles, Schmitt, Stocker and Fischer2017) and 14C production changes (Reimer et al. Reference Reimer, Austin, Bard, Bayliss, Blackwell, Ramsey, Butzin, Cheng, Edwards and Friedrich2020), as well as large-scale changes to ocean circulation (e.g., Böhm et al. Reference Böhm, Lippold, Gutjahr, Frank, Blaser, Antz, Fohlmeister, Frank, Andersen and Deininger2015; Henry et al. Reference Henry, McManus, Curry, Roberts, Piotrowski and Keigwin2016; Hodell et al. Reference Hodell, Venz, Charles and Ninnemann2003; Oka et al. Reference Oka, Abe-Ouchi, Sherriff-Tadano, Yokoyama, Kawamura and Hasumi2021) and air-sea gas exchange rates (e.g., Kageyama et al. Reference Kageyama, Harrison, Kapsch, Lofverstrom, Lora, Mikolajewicz, Sherriff-Tadano, Vadsaria, Abe-Ouchi and Bouttes2021; Kohfeld et al. Reference Kohfeld, Graham, de Boer, Sime, Wolff, Le Quéré and Bopp2013; McGee et al. Reference McGee, Broecker and Winckler2010). Crucially, the smoothing of the high frequency atmospheric 14C-age variation which is inherent to the ocean is also predominantly incorporated into this
${\rm{\Delta }}{R^{Location}}\left( \theta \right)$
the local-scale depletion factors. Global-scale factors include atmospheric CO2 (Köhler et al. Reference Köhler, Nehrbass-Ahles, Schmitt, Stocker and Fischer2017) and 14C production changes (Reimer et al. Reference Reimer, Austin, Bard, Bayliss, Blackwell, Ramsey, Butzin, Cheng, Edwards and Friedrich2020), as well as large-scale changes to ocean circulation (e.g., Böhm et al. Reference Böhm, Lippold, Gutjahr, Frank, Blaser, Antz, Fohlmeister, Frank, Andersen and Deininger2015; Henry et al. Reference Henry, McManus, Curry, Roberts, Piotrowski and Keigwin2016; Hodell et al. Reference Hodell, Venz, Charles and Ninnemann2003; Oka et al. Reference Oka, Abe-Ouchi, Sherriff-Tadano, Yokoyama, Kawamura and Hasumi2021) and air-sea gas exchange rates (e.g., Kageyama et al. Reference Kageyama, Harrison, Kapsch, Lofverstrom, Lora, Mikolajewicz, Sherriff-Tadano, Vadsaria, Abe-Ouchi and Bouttes2021; Kohfeld et al. Reference Kohfeld, Graham, de Boer, Sime, Wolff, Le Quéré and Bopp2013; McGee et al. Reference McGee, Broecker and Winckler2010). Crucially, the smoothing of the high frequency atmospheric 14C-age variation which is inherent to the ocean is also predominantly incorporated into this
![]() ${R^{GlobalAv}}\left( \theta \right)$
. More local-scale effects, which are incorporated through
${R^{GlobalAv}}\left( \theta \right)$
. More local-scale effects, which are incorporated through
![]() ${\rm{\Delta }}{R^{Location}}\left( \theta \right)$
and might have a further influence on the MRA in a specific area of study, include the depth of the ocean at that location, the presence of sea-ice, regional winds, and coastal upwelling (Key Reference Key2001; Key et al. Reference Key, Kozyr, Sabine, Lee, Wanninkhof, Bullister, Feely, Millero, Mordy and Peng2004; Reimer and Reimer Reference Reimer and Reimer2001; Toggweiler et al. Reference Toggweiler, Druffel, Key and Galbraith2019).
${\rm{\Delta }}{R^{Location}}\left( \theta \right)$
and might have a further influence on the MRA in a specific area of study, include the depth of the ocean at that location, the presence of sea-ice, regional winds, and coastal upwelling (Key Reference Key2001; Key et al. Reference Key, Kozyr, Sabine, Lee, Wanninkhof, Bullister, Feely, Millero, Mordy and Peng2004; Reimer and Reimer Reference Reimer and Reimer2001; Toggweiler et al. Reference Toggweiler, Druffel, Key and Galbraith2019).
Notation: The estimates of both
![]() ${R^{GlobalAv}}\left( \theta \right)$
and
${R^{GlobalAv}}\left( \theta \right)$
and
![]() ${\rm{\Delta }}{R^{Location}}\left( \theta \right)$
are updated with each MarineXX iteration as our knowledge increases. We use a subscript to denote which calibration curve we are referring to, so that
${\rm{\Delta }}{R^{Location}}\left( \theta \right)$
are updated with each MarineXX iteration as our knowledge increases. We use a subscript to denote which calibration curve we are referring to, so that
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
and
$R_{20}^{GlobalAv}\left( \theta \right)$
and
![]() $\Delta {R_{20}}\left( \theta \right)\;$
refer to the Marine20 estimates of global-scale and the local-scale depletion effects (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020). We also drop the location superscript in
$\Delta {R_{20}}\left( \theta \right)\;$
refer to the Marine20 estimates of global-scale and the local-scale depletion effects (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020). We also drop the location superscript in
![]() $\Delta {R^{Location}}$
where it is not essential for comprehension. A glossary of the key notation can be found in Table A1 (Appendix A).
$\Delta {R^{Location}}$
where it is not essential for comprehension. A glossary of the key notation can be found in Table A1 (Appendix A).
1.2 The Marine20 calibration curve and ΔR(θ) in polar regions
The Marine20 estimates (and all earlier marine calibration curves) only aim to model the global-scale changes in oceanic 14C levels, i.e.,
![]() ${R^{GlobalAv}}\left( \theta \right)$
. In any specific oceanic location, at any particular time
${R^{GlobalAv}}\left( \theta \right)$
. In any specific oceanic location, at any particular time
![]() $\theta $
, there is expected to be some additional localized 14C variation. This must be accounted for through the
$\theta $
, there is expected to be some additional localized 14C variation. This must be accounted for through the
![]() ${\rm{\Delta }}R\left( \theta \right)$
term. While we expect
${\rm{\Delta }}R\left( \theta \right)$
term. While we expect
![]() ${\rm{\Delta }}R\left( \theta \right)$
to vary over time, we do not currently have sufficient knowledge to be able to accurately model these changes or, in most locations, to estimate them with sufficient precision from data (Heaton et al. Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022).
${\rm{\Delta }}R\left( \theta \right)$
to vary over time, we do not currently have sufficient knowledge to be able to accurately model these changes or, in most locations, to estimate them with sufficient precision from data (Heaton et al. Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022).
To allow the community to calibrate marine 14C samples, we must therefore make a considerable simplification. The standard approach, taken since the first Marine calibration curve of Stuiver et al. (Reference Stuiver, Pearson and Braziunas1986), is to consider
![]() ${\rm{\Delta }}R\left( \theta \right)$
as being approximately constant (or at most to vary slowly) over time, i.e.,
${\rm{\Delta }}R\left( \theta \right)$
as being approximately constant (or at most to vary slowly) over time, i.e.,
![]() ${\rm{\Delta }}R\left( \theta \right) \equiv \;{\rm{\Delta }}R$
. We can estimate these regional values,
${\rm{\Delta }}R\left( \theta \right) \equiv \;{\rm{\Delta }}R$
. We can estimate these regional values,
![]() ${\rm{\Delta }}{R_{20}}$
in the case of the Marine20 curve, using 14C observations from the recent past. Such reference 14C samples and estimates of
${\rm{\Delta }}{R_{20}}$
in the case of the Marine20 curve, using 14C observations from the recent past. Such reference 14C samples and estimates of
![]() ${\rm{\Delta }}{R_{20}}$
are available, for example, in the maintained database at http://calib.org/marine/ (Reimer and Reimer Reference Reimer and Reimer2001). Having made such a simplification, to calibrate a new 14C sample we subtract the appropriate regional
${\rm{\Delta }}{R_{20}}$
are available, for example, in the maintained database at http://calib.org/marine/ (Reimer and Reimer Reference Reimer and Reimer2001). Having made such a simplification, to calibrate a new 14C sample we subtract the appropriate regional
![]() ${\rm{\Delta }}{R_{20}}$
from the observed radiocarbon age of the sample, and then calibrate against Marine20.
${\rm{\Delta }}{R_{20}}$
from the observed radiocarbon age of the sample, and then calibrate against Marine20.
This approach to calibration, assuming that
![]() ${\rm{\Delta }}R\left( \theta \right) \equiv {\rm{\Delta }}R$
, is recognized as being a coarse approximation for any ocean location. However, it is seen as a necessary simplification to enable a standardized approach to marine calibration until our knowledge improves (Heaton et al. Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022). However, in polar regions, the assumption of a constant
${\rm{\Delta }}R\left( \theta \right) \equiv {\rm{\Delta }}R$
, is recognized as being a coarse approximation for any ocean location. However, it is seen as a necessary simplification to enable a standardized approach to marine calibration until our knowledge improves (Heaton et al. Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022). However, in polar regions, the assumption of a constant
![]() ${\rm{\Delta }}R\left( \theta \right)$
over time cannot be justified. During glacial periods, outside ca. 40ºS–40ºN, we expect localized sea-ice cover, strong winds, and ocean circulation changes may have had substantial additional short-term effects on
${\rm{\Delta }}R\left( \theta \right)$
over time cannot be justified. During glacial periods, outside ca. 40ºS–40ºN, we expect localized sea-ice cover, strong winds, and ocean circulation changes may have had substantial additional short-term effects on
![]() ${\rm{\Delta }}R\left( \theta \right)$
(Butzin et al. Reference Butzin, Prange and Lohmann2005; Völker and Köhler Reference Völker and Köhler2013). Pre-Holocene/glacial values of
${\rm{\Delta }}R\left( \theta \right)$
(Butzin et al. Reference Butzin, Prange and Lohmann2005; Völker and Köhler Reference Völker and Köhler2013). Pre-Holocene/glacial values of
![]() $\Delta R\left( \theta \right)$
may therefore be considerably larger than the values of
$\Delta R\left( \theta \right)$
may therefore be considerably larger than the values of
![]() $\Delta R\left( \theta \right)$
during the Holocene/recent past (Butzin et al. Reference Butzin, Köhler and Lohmann2017; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019).
$\Delta R\left( \theta \right)$
during the Holocene/recent past (Butzin et al. Reference Butzin, Köhler and Lohmann2017; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019).
When calibrating 14C samples that arise from marine locations outside ca. 40ºS–40ºN and are older than ca. 11.5 cal kyr BP, it is therefore not appropriate to calibrate against any MarineXX curve using a value of
![]() ${\rm{\Delta }}R$
estimated from Holocene/recent past samples. If we fail to take the potentially increased
${\rm{\Delta }}R$
estimated from Holocene/recent past samples. If we fail to take the potentially increased
![]() ${\rm{\Delta }}R\left( \theta \right)$
into account during calibration, we are likely to introduce substantial biases in the resultant calendar age estimates: providing estimates for the calendar ages of glacial-period marine 14C samples in polar regions that are significantly older than their true calendar ages, and which underestimate the calendar age uncertainty.
${\rm{\Delta }}R\left( \theta \right)$
into account during calibration, we are likely to introduce substantial biases in the resultant calendar age estimates: providing estimates for the calendar ages of glacial-period marine 14C samples in polar regions that are significantly older than their true calendar ages, and which underestimate the calendar age uncertainty.
Glacial increases in
![]() ${\rm{\Delta }}R\left( \theta \right)$
at high-latitudes are predominantly driven by the increased coverage of sea-ice in these polar regions. Sea-ice restricts air-sea gas exchange, hence slowing the uptake of new atmospheric 14CO2 into the surface ocean. It is commonly assumed that sea-ice is impermeable for 14CO2, and that formation and melting of sea-ice do not change the concentration of dissolved inorganic 14C in the surface ocean. Under these assumptions, all air-sea exchange will vanish in fully ice-covered areas and the 14C concentrations of the surface water will reflect the greater depletion of deeper or remote waters. While we are able to model the effect of sea-ice on surface ocean 14C depletion, we lack sufficient knowledge over the glacial period on the appropriate climate scenario (and the extent of sea-ice at high latitudes) to use for that modeling. Over the course of the glacial, the climate and the extent of sea-ice are not expected to remain constant but rather to vary substantially over time.
${\rm{\Delta }}R\left( \theta \right)$
at high-latitudes are predominantly driven by the increased coverage of sea-ice in these polar regions. Sea-ice restricts air-sea gas exchange, hence slowing the uptake of new atmospheric 14CO2 into the surface ocean. It is commonly assumed that sea-ice is impermeable for 14CO2, and that formation and melting of sea-ice do not change the concentration of dissolved inorganic 14C in the surface ocean. Under these assumptions, all air-sea exchange will vanish in fully ice-covered areas and the 14C concentrations of the surface water will reflect the greater depletion of deeper or remote waters. While we are able to model the effect of sea-ice on surface ocean 14C depletion, we lack sufficient knowledge over the glacial period on the appropriate climate scenario (and the extent of sea-ice at high latitudes) to use for that modeling. Over the course of the glacial, the climate and the extent of sea-ice are not expected to remain constant but rather to vary substantially over time.
Location-specific estimates of the overall open-ocean surface water 14C depletion (i.e.,
![]() ${R^{Location}}\left( \theta \right)$
, the total MRA) are available under fixed carbon cycle and climate scenarios via the Hamburg Large Scale Geostrophic Ocean General Circulation Model (LSG OGCM, discussed in Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020) at https://doi.pangaea.de/10.1594/PANGAEA.914500. In principle, these LSG OGCM estimates could be used for polar 14C calibration, by adjusting the IntCal20 curve. However, the LSG OGCM scenarios provided are not transient, in terms of climate, and so calibrating under any individual scenario will still lead to overconfidence in the resultant age estimate. Further, the limited spatial resolution of the LSG OGCM means that estimation of a further regional depletion term, a
${R^{Location}}\left( \theta \right)$
, the total MRA) are available under fixed carbon cycle and climate scenarios via the Hamburg Large Scale Geostrophic Ocean General Circulation Model (LSG OGCM, discussed in Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020) at https://doi.pangaea.de/10.1594/PANGAEA.914500. In principle, these LSG OGCM estimates could be used for polar 14C calibration, by adjusting the IntCal20 curve. However, the LSG OGCM scenarios provided are not transient, in terms of climate, and so calibrating under any individual scenario will still lead to overconfidence in the resultant age estimate. Further, the limited spatial resolution of the LSG OGCM means that estimation of a further regional depletion term, a
![]() ${\rm{\Delta }}{R^{LSG}}$
, is still required. Direct calibration using the LSG OGCM estimates is therefore non-trivial using current software.
${\rm{\Delta }}{R^{LSG}}$
, is still required. Direct calibration using the LSG OGCM estimates is therefore non-trivial using current software.
1.3 A Simple Recommendation for Marine Polar 14C Calibration
In this paper, we suggest how a user might calibrate high latitude (outside ca. 40ºS–40ºN) marine 14C samples in such a way as to reduce the potential for bias and overconfidence in the resultant calendar age estimates. Since detail on past polar climate and the extent of sea-ice is largely unknown, and as we wish to retain simplicity in calibration, our proposal is, by necessity, a coarse approximation. We suggest modifying the
![]() ${\rm{\Delta }}R\left( \theta \right)$
used for calibration dependent upon whether the sample arose during glacial, or Holocene/interglacial, conditions. Our suggestion is informed by the LSG OGCM scenarios while still retaining use of the Marine20 curve.
${\rm{\Delta }}R\left( \theta \right)$
used for calibration dependent upon whether the sample arose during glacial, or Holocene/interglacial, conditions. Our suggestion is informed by the LSG OGCM scenarios while still retaining use of the Marine20 curve.
The application of a glacial increase in
![]() ${\rm{\Delta }}R\left( \theta \right)$
will have the effect of shifting the calibrated age estimate towards more recent dates. Hence, to determine if the 14C sample potentially lies in the glacial, we can calibrate first using just the lower depletion approach (see Section 1.3.1) with a modern-day
${\rm{\Delta }}R\left( \theta \right)$
will have the effect of shifting the calibrated age estimate towards more recent dates. Hence, to determine if the 14C sample potentially lies in the glacial, we can calibrate first using just the lower depletion approach (see Section 1.3.1) with a modern-day
![]() ${\rm{\Delta }}{R_{20}}$
. If this (low-depletion) calibration provides a calendar age date which falls in the glacial period, then the calibration user should also perform an additional calibration as this sample may require a glacial
${\rm{\Delta }}{R_{20}}$
. If this (low-depletion) calibration provides a calendar age date which falls in the glacial period, then the calibration user should also perform an additional calibration as this sample may require a glacial
![]() ${\rm{\Delta }}R\left( \theta \right)$
increase (described in Section 1.3.2).
${\rm{\Delta }}R\left( \theta \right)$
increase (described in Section 1.3.2).
Note that while we use the term Holocene/glacial to denote the partition between the two suggested calibration approaches, we do not provide a precise calendar date as to when substantial changes in polar
![]() ${\rm{\Delta }}R\left( \theta \right)$
may have occurred. This decision, and the glacial boundary, should be made and justified by the calibration user, drawing on various lines of paleoclimatic-paleoceanographic evidence.
${\rm{\Delta }}R\left( \theta \right)$
may have occurred. This decision, and the glacial boundary, should be made and justified by the calibration user, drawing on various lines of paleoclimatic-paleoceanographic evidence.
1.3.1 Calibrating polar 14C samples from the Holocene (ca. 11,500–0 cal yr BP)
We suggest that those users calibrating polar 14C samples from the Holocene can calibrate directly against Marine20 using a standard estimate of
![]() ${\rm{\Delta }}{R_{20}}$
obtained via 14C samples from the Holocene (e.g., 14C samples from the recent past). This suggestion is based on the relatively stable climate during the Holocene period and an assumption that, even at high latitudes, we would not expect substantial sea-ice based temporal variations in
${\rm{\Delta }}{R_{20}}$
obtained via 14C samples from the Holocene (e.g., 14C samples from the recent past). This suggestion is based on the relatively stable climate during the Holocene period and an assumption that, even at high latitudes, we would not expect substantial sea-ice based temporal variations in
![]() ${\rm{\Delta }}R\left( \theta \right)$
. Such a
${\rm{\Delta }}R\left( \theta \right)$
. Such a
![]() ${\rm{\Delta }}{R_{20}}$
estimate can be obtained using samples from the recent past via the maintained database at http://calib.org/marine/ (Reimer and Reimer Reference Reimer and Reimer2001) or from paired radiocarbon dated marine/terrestrial samples. During the Holocene, the approach to calibration of polar samples therefore remains the same as that traditionally taken for any other marine location. This retains consistency.
${\rm{\Delta }}{R_{20}}$
estimate can be obtained using samples from the recent past via the maintained database at http://calib.org/marine/ (Reimer and Reimer Reference Reimer and Reimer2001) or from paired radiocarbon dated marine/terrestrial samples. During the Holocene, the approach to calibration of polar samples therefore remains the same as that traditionally taken for any other marine location. This retains consistency.
If this calibration, with a Holocene-based estimate of
![]() ${\rm{\Delta }}{R_{20}}$
, provides an estimate for the calendar age which lies entirely in the Holocene, then we can be confident the sample arises from this period. The user can then stop after this single calibration and report their calibrated age interval. However, if the calibrated age extends into the glacial (beyond approximately 11,500 cal yr BP), the sample may require a glacial polar
${\rm{\Delta }}{R_{20}}$
, provides an estimate for the calendar age which lies entirely in the Holocene, then we can be confident the sample arises from this period. The user can then stop after this single calibration and report their calibrated age interval. However, if the calibrated age extends into the glacial (beyond approximately 11,500 cal yr BP), the sample may require a glacial polar
![]() ${\rm{\Delta }}R\left( \theta \right)$
boost and the user should follow Section 1.3.2.
${\rm{\Delta }}R\left( \theta \right)$
boost and the user should follow Section 1.3.2.
Note: We recognize that there is a scarcity of modern
![]() ${\rm{\Delta }}{R_{20}}$
values in the maintained http://calib.org/marine/ database for some specific regions and locations. In regions without substantial vertical ocean mixing, we suggest that users may consider the origin of the ocean surface water based upon the currents involved and select a
${\rm{\Delta }}{R_{20}}$
values in the maintained http://calib.org/marine/ database for some specific regions and locations. In regions without substantial vertical ocean mixing, we suggest that users may consider the origin of the ocean surface water based upon the currents involved and select a
![]() ${\rm{\Delta }}{R_{20}}$
based on the appropriate values in those origins. Information on currents can be obtained through the Ocean Current Regimes tab within the http://calib.org/marine/ database.
${\rm{\Delta }}{R_{20}}$
based on the appropriate values in those origins. Information on currents can be obtained through the Ocean Current Regimes tab within the http://calib.org/marine/ database.
1.3.2 Calibrating polar 14C samples from glacial periods (ca. 55,000–11,500 cal yr BP)
For those users wishing to calibrate high-latitude samples from glacial periods, we propose the application of a latitude-dependent adjustment to the value of
![]() ${\rm{\Delta }}{R_{20}}$
. This adjustment aims to account for potential glacial changes in regional 14C depletion within polar oceans due to localized sea-ice and other local factors. Specifically, during glacial periods, we suggest that a user consider two distinct
${\rm{\Delta }}{R_{20}}$
. This adjustment aims to account for potential glacial changes in regional 14C depletion within polar oceans due to localized sea-ice and other local factors. Specifically, during glacial periods, we suggest that a user consider two distinct
![]() ${\rm{\Delta }}{R_{20}}$
polar depletion scenarios providing bracketing glacial climates:
${\rm{\Delta }}{R_{20}}$
polar depletion scenarios providing bracketing glacial climates:
-
1. Minimal polar 14C glacial depletion—Calibrate against Marine20 applying a
 ${\rm{\Delta }}R_{20}^{Hol}$
that matches the adjustment for regional 14C depletion seen during the Holocene. As for Section 1.3.1, this
${\rm{\Delta }}R_{20}^{Hol}$
that matches the adjustment for regional 14C depletion seen during the Holocene. As for Section 1.3.1, this
 ${\rm{\Delta }}R_{20}^{Hol}\;$
can be calculated using 14C samples from the recent past such as those found in the maintained database at http://calib.org/marine/ (Reimer and Reimer Reference Reimer and Reimer2001).
${\rm{\Delta }}R_{20}^{Hol}\;$
can be calculated using 14C samples from the recent past such as those found in the maintained database at http://calib.org/marine/ (Reimer and Reimer Reference Reimer and Reimer2001). -
2. Maximal polar 14C glacial depletion—Apply an increase to the Holocene-based
 ${\rm{\Delta }}R_{20}^{Hol}$
to obtain a high-depletion
${\rm{\Delta }}R_{20}^{Hol}$
to obtain a high-depletion
 ${\rm{\Delta }}R_{20}^{GS} = {\rm{\Delta }}R_{20}^{Hol} + {\rm{\;\Delta }}R_{20}^{Hol\; \to \;GS}$
that is chosen to provide optimal agreement with the GS scenario of the LSG OGCM. Calibrate against Marine20 using this increased
${\rm{\Delta }}R_{20}^{GS} = {\rm{\Delta }}R_{20}^{Hol} + {\rm{\;\Delta }}R_{20}^{Hol\; \to \;GS}$
that is chosen to provide optimal agreement with the GS scenario of the LSG OGCM. Calibrate against Marine20 using this increased
 ${\rm{\Delta }}R_{20}^{GS}$
.
${\rm{\Delta }}R_{20}^{GS}$
.
The proposed increase, i.e.,
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
, that is required to transform
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
, that is required to transform
![]() ${\rm{\Delta }}R_{20}^{Hol}$
into
${\rm{\Delta }}R_{20}^{Hol}$
into
![]() ${\rm{\Delta }}R_{20}^{GS}$
is dependent upon the latitude of the sample. The values of
${\rm{\Delta }}R_{20}^{GS}$
is dependent upon the latitude of the sample. The values of
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
at each latitude are shown in Figure 1, with the values tabulated in Table A2 (Appendix A) and available as an Excel spreadsheet in Supplementary Information D. Calibrating against Marine20 first with the low-depletion
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
at each latitude are shown in Figure 1, with the values tabulated in Table A2 (Appendix A) and available as an Excel spreadsheet in Supplementary Information D. Calibrating against Marine20 first with the low-depletion
![]() ${\rm{\Delta }}R_{20}^{Hol}$
adjustment, and then separately with the high-depletion
${\rm{\Delta }}R_{20}^{Hol}$
adjustment, and then separately with the high-depletion
![]() ${\rm{\Delta }}R_{20}^{GS}\;$
scenario, should hopefully provide bracketing calibrated ages for the true calendar age of the sample.
${\rm{\Delta }}R_{20}^{GS}\;$
scenario, should hopefully provide bracketing calibrated ages for the true calendar age of the sample.

Figure 1 The latitudinal-average increase in oceanic 14C depletion,
![]() $\Delta R_{20}^{Hol\; \to \;GS}$
, needed to transform from Marine20 (with an initial Holocene
$\Delta R_{20}^{Hol\; \to \;GS}$
, needed to transform from Marine20 (with an initial Holocene
![]() $\Delta R_{20}^{Hol}$
) to the localized GS scenario estimates of the LSG OGCM. The shaded gray area represents the mean width (from 40,000–11,500 cal yr BP) of the ±2
$\Delta R_{20}^{Hol}$
) to the localized GS scenario estimates of the LSG OGCM. The shaded gray area represents the mean width (from 40,000–11,500 cal yr BP) of the ±2
![]() $\sigma $
uncertainty on Marine20’s
$\sigma $
uncertainty on Marine20’s
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
. The blue shaded area represents the 95% quantiles on the
$R_{20}^{GlobalAv}\left( \theta \right)$
. The blue shaded area represents the 95% quantiles on the
![]() $\Delta R_{20}^{Hol\; \to \;GS}$
shift required for the given latitude. (Please see online version for color figures.)
$\Delta R_{20}^{Hol\; \to \;GS}$
shift required for the given latitude. (Please see online version for color figures.)
Such an approach retains simplicity in calibration, allowing use of Marine20 and existing calibration software. A user is not required to create their own (location-specific) calibration curve since the proposed approach requires only an adjustment to
![]() ${\rm{\Delta }}{R_{20}}$
. This is typically available as an option in calibration software. Our suggested adjustment from
${\rm{\Delta }}{R_{20}}$
. This is typically available as an option in calibration software. Our suggested adjustment from
![]() ${\rm{\Delta }}R_{20}^{Hol}$
to
${\rm{\Delta }}R_{20}^{Hol}$
to
![]() ${\rm{\Delta }}R_{20}^{GS}$
depends only upon the latitude of the 14C sample we wish to calibrate (and not its specific longitude or ocean basin).
${\rm{\Delta }}R_{20}^{GS}$
depends only upon the latitude of the 14C sample we wish to calibrate (and not its specific longitude or ocean basin).
1.3.3 Additional considerations
Our current approach is only intended as a first approximation and hence is designed to be coarse. There is much that we still do not know about 14C levels at high-latitudes and our primary aim is to make users aware they must tread carefully when using calibrated dates based on 14C marine samples in polar regions. As we learn more about the past climatic conditions, we expect we will be able to provide more localized, detailed, and temporally varying adjustments to
![]() ${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
.
${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
.
In particular, due to the separation of the Pacific from the Atlantic and Arctic Ocean during the last glacial by a sea level drop that allowed the crossing of the Bering Strait on land (De Boer and Nof Reference De Boer and Nof2004; Jakobsson et al. Reference Jakobsson, Pearce, Cronin, Backman, Anderson, Barrientos, Björk, Coxall, de Boer and Mayer2017; Knudson and Ravelo Reference Knudson and Ravelo2015), we expect an ocean-basin dependent adjustment may be appropriate. For this study, we did investigate such a dependence (see Supplementary Information B and C, Figures S2 and S6) but felt that basin-specific adjustments would provide potentially spurious precision as they were predominantly due to model choice (in particular, the positioning of sea-ice).
We also note that some users may have independent paleoclimatic evidence as to the glacial conditions in their oceanic location, for example through proxy evidence within a sediment core. For such users, we still recommend they present our bracketing approach (i.e., both limiting depletion scenarios). However, they may then wish to use their expert knowledge to argue for one scenario as being more appropriate than the other (or indeed for an intermediate level of 14C depletion lying between the two low- and high- depletion extremes). With rigorous palaeoclimatic proxies, it may even be possible to scale the appropriate
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
to apply to each sample between the extreme
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
to apply to each sample between the extreme
![]() ${\rm{\Delta }}R_{20}^{Hol}$
and
${\rm{\Delta }}R_{20}^{Hol}$
and
![]() ${\rm{\Delta }}R_{20}^{GS}$
values. This offers the possibility to provide more precise calibrated age ranges.
${\rm{\Delta }}R_{20}^{GS}$
values. This offers the possibility to provide more precise calibrated age ranges.
Finally, we advise users to interpolate the boost
![]() $\Delta R_{20}^{Hol\; \to \;GS}$
for those latitudes not explicitly provided in Table A2 (Appendix). This will ensure smooth changes to calibrated ages. Those considering marine 14C samples that span a latitudinal range (e.g., from feeding birds) should create their
$\Delta R_{20}^{Hol\; \to \;GS}$
for those latitudes not explicitly provided in Table A2 (Appendix). This will ensure smooth changes to calibrated ages. Those considering marine 14C samples that span a latitudinal range (e.g., from feeding birds) should create their
![]() $\Delta R_{20}^{Hol\; \to \;GS}$
boost by averaging over that latitudinal range.
$\Delta R_{20}^{Hol\; \to \;GS}$
boost by averaging over that latitudinal range.
1.4 Paper Layout
The paper is set out as follows. In Section 2, we provide a short explanation of Marine20 (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020) which provides estimates of global
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
MRA effects. We then compare these to localized model estimates for open-ocean surface water 14C depletion from the LSG OGCM (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020) under three different scenarios (PD, GS and CS). We show how we can approximately transition from the global Marine20 to the various localized LSG OGCM estimates by applying a constant shift to
$R_{20}^{GlobalAv}\left( \theta \right)$
MRA effects. We then compare these to localized model estimates for open-ocean surface water 14C depletion from the LSG OGCM (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020) under three different scenarios (PD, GS and CS). We show how we can approximately transition from the global Marine20 to the various localized LSG OGCM estimates by applying a constant shift to
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
.
$R_{20}^{GlobalAv}\left( \theta \right)$
.
In Section 3, we summarize these shifts from Marine20’s
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
to obtain our suggested latitudinal increases
$R_{20}^{GlobalAv}\left( \theta \right)$
to obtain our suggested latitudinal increases
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
. These allow us to approximate the GS scenario of the LSG OGCM using the Marine20 curve. To further support our proposed bracketing approach, we compare the upper and lower bounds for
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
. These allow us to approximate the GS scenario of the LSG OGCM using the Marine20 curve. To further support our proposed bracketing approach, we compare the upper and lower bounds for
![]() ${R^{Location}}\left( \theta \right)$
obtained via our recommended adjustments to Marine20’s global-scale
${R^{Location}}\left( \theta \right)$
obtained via our recommended adjustments to Marine20’s global-scale
![]() $R_{20}^{GlobalAv}\left( \theta \right)\;$
against directly observed surface MRA estimates at the site of the deep-sea core MD04-2829 (59.0°N, 9.5°W; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019).
$R_{20}^{GlobalAv}\left( \theta \right)\;$
against directly observed surface MRA estimates at the site of the deep-sea core MD04-2829 (59.0°N, 9.5°W; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019).
We present worked examples of polar ocean 14C calibration using our bracketing approach in Section 4. We consider the calibration of individual samples as well as the construction of an age-depth model using deep-sea core MD02-2496 offshore of Vancouver Island at 49.0ºN, 127.0ºW (Cosma et al. Reference Cosma, Hendy and Chang2008; Taylor et al. Reference Taylor, Hendy and Pak2014). In this Section, we also briefly discuss how individuals might present their calibrated dates when they have independent proxy information on the appropriate depletion scenario. Finally in Section 5, we summarize our recommendations and describe avenues for future work.
2 Adjusting Marine20’s
 ${R^{Global}}\left( \theta \right)$
to Match Regional LSG OGCM Output
${R^{Global}}\left( \theta \right)$
to Match Regional LSG OGCM Output
2.1 Marine20 vs. LSG OGCM
Marine20 uses a transient application of the BICYCLE carbon cycle box model (Köhler et al. Reference Köhler, Muscheler and Fischer2006, Reference Köhler, Fischer and Schmitt2010). While Marine20 does incorporate the major changes in the global carbon cycle that occurred during the glacial, it only aims to summarize their wide-scale effect on large ocean areas. The resultant Marine20 curve, and its
![]() ${R^{Global}}\left( \theta \right)$
, should therefore only be viewed as providing a global-scale estimate of changes over time in oceanic 14C levels (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020, Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022). If there are additional localized effects in a study location that are temporally varying, for example, if regional sea-ice was not present during the Holocene but likely extensive during the glacial, then a Marine20 user must incorporate those effects through adjustments to the regional
${R^{Global}}\left( \theta \right)$
, should therefore only be viewed as providing a global-scale estimate of changes over time in oceanic 14C levels (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020, Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022). If there are additional localized effects in a study location that are temporally varying, for example, if regional sea-ice was not present during the Holocene but likely extensive during the glacial, then a Marine20 user must incorporate those effects through adjustments to the regional
![]() ${\rm{\Delta }}R\left( \theta \right)$
.
${\rm{\Delta }}R\left( \theta \right)$
.
The LSG OGCM (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020) is able to provide more localized ocean modeling, generating estimates of 14C levels and MRA at specific marine locations on a 2.5º by 2.5º grid (see Figure 2). However, the LSG OGCM is much slower to run than BICYCLE. The LSG OGCM estimates are run under fixed climate scenarios as well as being model-specific. This currently makes it difficult to use the LSG OGCM to fully understand the uncertainties in local MRAs since knowledge regarding the appropriate glacial climate and carbon cycle to apply is highly imprecise. LSG OGCM estimates of overall MRA are available, forced by the IntCal20 posterior mean for atmospheric 14C concentrations (Reimer et al. Reference Reimer, Austin, Bard, Bayliss, Blackwell, Ramsey, Butzin, Cheng, Edwards and Friedrich2020), under three specific climate scenarios (Butzin et al. Reference Butzin, Prange and Lohmann2005):
-
PD—a climate scenario intended to be very similar to the present day.
-
GS—a glacial climate scenario representing the Last Glacial Maximum (LGM), featuring a shallower AMOC weakened by about 30% compared to PD.
-
CS—a more extreme glacial climate scenario aiming to mimic cold stadials with further AMOC weakening by about 60% compared with PD.

Figure 2 Location-specific estimates, at 0 cal yr BP, of the overall MRA,
![]() ${R^{Location}}\left( \theta \right)$
, obtained by the LSG OGCM under the PD scenario. The plotting color represents the MRA value with scale shown on RHS (in 14C yrs); white represents land. Three line transects are shown passing through the South Pacific (purple 160ºW), North Pacific (yellow 170ºW), and North Atlantic and Arctic (green 20ºW). We highlight sample sites on each transect which are used later (in Figure 3) to illustrate the potential changes in surface-water 14C depletion under various glacial scenarios as we extend into higher-latitude oceans.
${R^{Location}}\left( \theta \right)$
, obtained by the LSG OGCM under the PD scenario. The plotting color represents the MRA value with scale shown on RHS (in 14C yrs); white represents land. Three line transects are shown passing through the South Pacific (purple 160ºW), North Pacific (yellow 170ºW), and North Atlantic and Arctic (green 20ºW). We highlight sample sites on each transect which are used later (in Figure 3) to illustrate the potential changes in surface-water 14C depletion under various glacial scenarios as we extend into higher-latitude oceans.
While designed to incorporate more of the localized variations in surface-ocean 14C depletion, the LSG OGCM estimates do not incorporate every potential influence and are model specific. Consequently, they still require a regional correction
![]() $\Delta {R^{LSG}}$
(equivalent to a
$\Delta {R^{LSG}}$
(equivalent to a
![]() ${\rm{\Delta }}{R_{20}}$
) if they are to be used for calibration. This
${\rm{\Delta }}{R_{20}}$
) if they are to be used for calibration. This
![]() $\Delta {R^{LSG}}$
would typically be obtained by comparing known-age 14C samples from the recent past against the corresponding PD scenario output from the nearest open-ocean LSG OGCM location (analogous to the calculation of a
$\Delta {R^{LSG}}$
would typically be obtained by comparing known-age 14C samples from the recent past against the corresponding PD scenario output from the nearest open-ocean LSG OGCM location (analogous to the calculation of a
![]() ${\rm{\Delta }}{R_{20}}$
). Using the LSG OGCM outputs directly for calibration is therefore non-trivial; and since they are run under fixed climate scenarios, calibration against any one scenario will still give overprecise calendar ages. However, we believe that the constant-state GS scenario provides a reasonable upper bound for the level of oceanic 14C depletion during the glacial. More detail on both construction of the BICYCLE/Marine20 and the LSG OGCM estimates can be found in Supplementary Information A.
${\rm{\Delta }}{R_{20}}$
). Using the LSG OGCM outputs directly for calibration is therefore non-trivial; and since they are run under fixed climate scenarios, calibration against any one scenario will still give overprecise calendar ages. However, we believe that the constant-state GS scenario provides a reasonable upper bound for the level of oceanic 14C depletion during the glacial. More detail on both construction of the BICYCLE/Marine20 and the LSG OGCM estimates can be found in Supplementary Information A.
To justify our proposed approach to polar calibration using Marine20, we demonstrate that a user can approximately recreate the regional LSG OGCM estimates while maintaining use of the global-scale Marine20 through a simple modification, or boost, to their
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
. Our approach relies on three key elements. Firstly, that each climate scenario of the LSG OGCM output can be approximated by applying a constant (not time dependent) shift to Marine20’s
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
. Our approach relies on three key elements. Firstly, that each climate scenario of the LSG OGCM output can be approximated by applying a constant (not time dependent) shift to Marine20’s
![]() $R_{20}^{Global}\left( \theta \right)$
. Consequently, we can effectively transition to the different LSG OGCM scenarios, while retaining the use of Marine20, just by applying a static (constant) shift to a present-day estimate of
$R_{20}^{Global}\left( \theta \right)$
. Consequently, we can effectively transition to the different LSG OGCM scenarios, while retaining the use of Marine20, just by applying a static (constant) shift to a present-day estimate of
![]() ${\rm{\Delta }}{R_{20}}$
. Secondly, in low-latitude locations (within 40ºS to 40ºN) the uncertainty bands on Marine20 already encapsulate the LSG OGCM scenarios. Thirdly, that by latitudinally averaging the boost required to match the LSG OGCM scenario, we reduce the influence of the model specificity of the LSG OGCM (for example, the precise location and dynamics of sea-ice and freshwater balance) and simplify the application of our proposed calibration approach.
${\rm{\Delta }}{R_{20}}$
. Secondly, in low-latitude locations (within 40ºS to 40ºN) the uncertainty bands on Marine20 already encapsulate the LSG OGCM scenarios. Thirdly, that by latitudinally averaging the boost required to match the LSG OGCM scenario, we reduce the influence of the model specificity of the LSG OGCM (for example, the precise location and dynamics of sea-ice and freshwater balance) and simplify the application of our proposed calibration approach.
We propose using the GS scenario of the LSG OGCM as the upper bound for surface ocean 14C depletion in the glacial. However, should a user decide that they wish to bound their glacial climate with the more extreme CS scenario, a similar set of findings hold. The corresponding CS-based upper bound on the glacial boost to
![]() ${\rm{\Delta }}{R_{20}}$
can be found in Table A2 (Appendix) and the Supplementary Information (Figures S3–S6 in Supplementary Info C, and accompanying spreadsheet in Supplementary Info D).
${\rm{\Delta }}{R_{20}}$
can be found in Table A2 (Appendix) and the Supplementary Information (Figures S3–S6 in Supplementary Info C, and accompanying spreadsheet in Supplementary Info D).
2.2 Illustrative Regional Estimates of MRA
The LSG OGCM surface-water estimates are provided every 50 cal yrs for open ocean regions. For both the GS and CS scenarios, the Pacific was disconnected from the Arctic Ocean because the Bering Strait (which is currently shallower than 50 m in depth) was closed during the glacial sea-level lowstand (Jakobsson et al. Reference Jakobsson, Pearce, Cronin, Backman, Anderson, Barrientos, Björk, Coxall, de Boer and Mayer2017). Global sea-levels during the glacial are believed to have been in the order of 130m lower than those of the present day (Lambeck et al. Reference Lambeck, Rouby, Purcell, Sun and Sambridge2014).
To illustrate our proposed approach, we consider three transects (Figure 2). The first (in purple) passes through the Southern Pacific Ocean at a longitude of 160ºW. The second (in yellow) through the Northern Pacific at a longitude of 170ºW. During the glacial period this transect becomes cut-off from the Arctic Ocean further North by closure of the Bering Strait. The third transect (in green) passes through the Atlantic and into the Arctic at a longitude of 20ºW. The estimates along these transects are typical of the LSG OGCM outputs. In Figure 2, we plot the spatial MRA estimates provided by the LSG OGCM under the PD scenario at 0 cal yr BP (i.e., 1950 CE).
To enable comparison of the LSG OGCM estimates with Marine20 we must account for the shifts (denoted
![]() ${\rm{\Delta }}{R^{LSG}}$
and
${\rm{\Delta }}{R^{LSG}}$
and
![]() ${\rm{\Delta }}{R_{20}}$
respectively) that would need to be applied to each estimate. For each location, we have calculated the difference between the mean (in 14C yrs) of the PD scenario of the LSG OGCM from 11,500–0 cal yr BP and the mean of the
${\rm{\Delta }}{R_{20}}$
respectively) that would need to be applied to each estimate. For each location, we have calculated the difference between the mean (in 14C yrs) of the PD scenario of the LSG OGCM from 11,500–0 cal yr BP and the mean of the
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
in the same period. This difference has then been used to shift both the PD and GS outputs of the LSG OGCM for that location. Figure 3 presents these shifted location-specific estimates of the MRA over time along the three selected transects under both the PD and GS scenario of the LSG OGCM; and the equivalent estimates with Marine20. For each location, the mean over the 11,500–0 cal yr BP period of
$R_{20}^{GlobalAv}\left( \theta \right)$
in the same period. This difference has then been used to shift both the PD and GS outputs of the LSG OGCM for that location. Figure 3 presents these shifted location-specific estimates of the MRA over time along the three selected transects under both the PD and GS scenario of the LSG OGCM; and the equivalent estimates with Marine20. For each location, the mean over the 11,500–0 cal yr BP period of
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
and the shift-adjusted PD outputs of the LSG OGCM are equal. Applying such a shift to both the PD and GS outputs of the LSG OGCM enables comparison between the calibration one would achieve using Marine20 (with a constant estimate of
$R_{20}^{GlobalAv}\left( \theta \right)$
and the shift-adjusted PD outputs of the LSG OGCM are equal. Applying such a shift to both the PD and GS outputs of the LSG OGCM enables comparison between the calibration one would achieve using Marine20 (with a constant estimate of
![]() ${\rm{\Delta }}{R_{20}}$
based on recent-past/Holocene 14C data), and that obtained using the LSG OGCM outputs (with a constant
${\rm{\Delta }}{R_{20}}$
based on recent-past/Holocene 14C data), and that obtained using the LSG OGCM outputs (with a constant
![]() $\Delta {R^{LSG}}$
based on the same recent-past/Holocene 14C data). We do not show the GS estimates from 11,500–0 cal yr BP as this climate scenario is inappropriate for the Holocene.
$\Delta {R^{LSG}}$
based on the same recent-past/Holocene 14C data). We do not show the GS estimates from 11,500–0 cal yr BP as this climate scenario is inappropriate for the Holocene.

Figure 3 Comparing the Marine20, PD and GS estimates for the MRA at marine locations along the line transects shown in Figure 2 passing through the: (a) South Pacific Ocean; (b) North Pacific Ocean; (c) North Atlantic and Arctic Oceans. Shown in black is the estimate of
![]() ${\rm{R}}_{20}^{{\rm{GlobalAv}}}\left( {\rm{\theta }} \right)$
used in Marine20 together with its 2
${\rm{R}}_{20}^{{\rm{GlobalAv}}}\left( {\rm{\theta }} \right)$
used in Marine20 together with its 2
![]() ${\rm{\sigma }}$
interval (gray shaded region). The GS and PD estimates from the LSG OGCM have been shifted so that the mean of the plotted PD scenario in each location agrees with the mean of
${\rm{\sigma }}$
interval (gray shaded region). The GS and PD estimates from the LSG OGCM have been shifted so that the mean of the plotted PD scenario in each location agrees with the mean of
![]() ${\rm{R}}_{20}^{{\rm{GlobalAv}}}\left( {\rm{\theta }} \right)$
from 11,500–0 cal yr BP. The shifted PD scenario for each latitude on the transect is shown as a (variously colored) solid line and the shifted GS scenario as a matched dashed line. The vertical line represents 11,500 cal yr BP. GS estimates from the LSG OGCM are not provided for calendar ages more recent than this.
${\rm{R}}_{20}^{{\rm{GlobalAv}}}\left( {\rm{\theta }} \right)$
from 11,500–0 cal yr BP. The shifted PD scenario for each latitude on the transect is shown as a (variously colored) solid line and the shifted GS scenario as a matched dashed line. The vertical line represents 11,500 cal yr BP. GS estimates from the LSG OGCM are not provided for calendar ages more recent than this.
Figure 3 effectively illustrates the difference, at a specific location, in overall MRA one would obtain using Marine20 compared with the PD and GS scenarios of the LSG OGCM. The difference between the PD (colored solid lines) and GS (dashed lines) estimates between 55,000–11,500 cal yr BP show how much additional 14C depletion, according to the LSG OGCM, is modeled at that ocean location by changing from a Holocene-type (PD) scenario to a glacial (GS) scenario. The difference between the
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
of Marine20 (solid black line) and the adjusted GS estimates show how much additional localized 14C depletion might have occurred, beyond that already incorporated within the global-scale estimate of Marine20, under a GS glacial scenario. These location-dependent increases from
$R_{20}^{GlobalAv}\left( \theta \right)$
of Marine20 (solid black line) and the adjusted GS estimates show how much additional localized 14C depletion might have occurred, beyond that already incorporated within the global-scale estimate of Marine20, under a GS glacial scenario. These location-dependent increases from
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
must be incorporated into
$R_{20}^{GlobalAv}\left( \theta \right)$
must be incorporated into
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
if we wish to represent the GS scenario with Marine20. Similar plots for the more extreme CS scenario of the LSG OGCM can be found in the Supplementary Information C (Figures S3 and S4).
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
if we wish to represent the GS scenario with Marine20. Similar plots for the more extreme CS scenario of the LSG OGCM can be found in the Supplementary Information C (Figures S3 and S4).
2.3 Comparing the LSG OGCM and Marine20
Several observations are immediately apparent from Figure 3. Firstly, during the Holocene, once we have estimated both a
![]() ${\rm{\Delta }}{R_{20}}$
and a
${\rm{\Delta }}{R_{20}}$
and a
![]() ${\rm{\Delta }}{R^{LSG}}$
regional/coastal adjustment based on modern 14C samples, the PD scenario from the LSG OGCM provides very similar MRA estimates to Marine20 for all the ocean locations on our sample transects. As we extend into the very high latitudes in the Southern Pacific and Arctic Ocean, the PD scenario does perhaps suggest slightly greater variations in MRA, in terms of the change from the levels of 14C depletion seen at the beginning of the Holocene compared to the present day, than Marine20. However, these changes are minor and generally lie within the uncertainty bands of Marine20. Intuitively, the uncertainty bands of Marine20 result from considering multiple potential climate and carbon cycle scenarios. It is likely that, during the Holocene, one of these (BICYCLE-based) scenarios lies extremely close to the PD scenario of the LSG OGCM. Consequently, for samples between 11,500–0 cal yr BP, there should be little difference between calibrating at sites along our transects using the PD output from LSG OGCM (with a
${\rm{\Delta }}{R^{LSG}}$
regional/coastal adjustment based on modern 14C samples, the PD scenario from the LSG OGCM provides very similar MRA estimates to Marine20 for all the ocean locations on our sample transects. As we extend into the very high latitudes in the Southern Pacific and Arctic Ocean, the PD scenario does perhaps suggest slightly greater variations in MRA, in terms of the change from the levels of 14C depletion seen at the beginning of the Holocene compared to the present day, than Marine20. However, these changes are minor and generally lie within the uncertainty bands of Marine20. Intuitively, the uncertainty bands of Marine20 result from considering multiple potential climate and carbon cycle scenarios. It is likely that, during the Holocene, one of these (BICYCLE-based) scenarios lies extremely close to the PD scenario of the LSG OGCM. Consequently, for samples between 11,500–0 cal yr BP, there should be little difference between calibrating at sites along our transects using the PD output from LSG OGCM (with a
![]() ${\rm{\Delta }}{R^{LSG}}$
adjustment) and using Marine20 (with a regional
${\rm{\Delta }}{R^{LSG}}$
adjustment) and using Marine20 (with a regional
![]() ${\rm{\Delta }}{R_{20}}$
). This is the case for both polar and equatorial regions.
${\rm{\Delta }}{R_{20}}$
). This is the case for both polar and equatorial regions.
Secondly, from 55,000–11,500 cal yr BP, we can see that (after the
![]() ${\rm{\Delta }}{R_{20}}$
and
${\rm{\Delta }}{R_{20}}$
and
![]() ${\rm{\Delta }}{R^{LSG}}$
shift/adjustment) the PD scenario of the LSG OGCM (colored solid lines) tends to generate estimates of the overall MRA along our transects that are lower than those of Marine20 (solid black line). This highlights that, while not able to resolve regionally, Marine20 does incorporate global effects of climatic and carbon cycle changes during the glacial. In this pre-Holocene period, the PD scenario of the LSG OGCM is unlikely to be appropriate as we know there were substantial global changes in the climate and carbon cycle between the glacial and the present day (Böhm et al. Reference Böhm, Lippold, Gutjahr, Frank, Blaser, Antz, Fohlmeister, Frank, Andersen and Deininger2015; Henry et al. Reference Henry, McManus, Curry, Roberts, Piotrowski and Keigwin2016; Kageyama et al. Reference Kageyama, Harrison, Kapsch, Lofverstrom, Lora, Mikolajewicz, Sherriff-Tadano, Vadsaria, Abe-Ouchi and Bouttes2021; Oka et al. Reference Oka, Abe-Ouchi, Sherriff-Tadano, Yokoyama, Kawamura and Hasumi2021; Petit et al. Reference Petit, Mourner, Jouzel, Korotkevich, Kotlyakov and Lorius1990). We expect that, from 55,000–11,500 cal yr BP, the true level of oceanic 14C depletion at a site will therefore be bounded below by the (
${\rm{\Delta }}{R^{LSG}}$
shift/adjustment) the PD scenario of the LSG OGCM (colored solid lines) tends to generate estimates of the overall MRA along our transects that are lower than those of Marine20 (solid black line). This highlights that, while not able to resolve regionally, Marine20 does incorporate global effects of climatic and carbon cycle changes during the glacial. In this pre-Holocene period, the PD scenario of the LSG OGCM is unlikely to be appropriate as we know there were substantial global changes in the climate and carbon cycle between the glacial and the present day (Böhm et al. Reference Böhm, Lippold, Gutjahr, Frank, Blaser, Antz, Fohlmeister, Frank, Andersen and Deininger2015; Henry et al. Reference Henry, McManus, Curry, Roberts, Piotrowski and Keigwin2016; Kageyama et al. Reference Kageyama, Harrison, Kapsch, Lofverstrom, Lora, Mikolajewicz, Sherriff-Tadano, Vadsaria, Abe-Ouchi and Bouttes2021; Oka et al. Reference Oka, Abe-Ouchi, Sherriff-Tadano, Yokoyama, Kawamura and Hasumi2021; Petit et al. Reference Petit, Mourner, Jouzel, Korotkevich, Kotlyakov and Lorius1990). We expect that, from 55,000–11,500 cal yr BP, the true level of oceanic 14C depletion at a site will therefore be bounded below by the (
![]() ${\rm{\Delta }}{R_{20}}$
-adjusted) Marine20 rather than the (
${\rm{\Delta }}{R_{20}}$
-adjusted) Marine20 rather than the (
![]() ${\rm{\Delta }}{R^{LSG}}$
-adjusted) PD scenario of the LSG OGCM.
${\rm{\Delta }}{R^{LSG}}$
-adjusted) PD scenario of the LSG OGCM.
Thirdly, if we consider the (
![]() ${\rm{\Delta }}{R^{LSG}}$
-adjusted) GS scenario estimates (dashed lines) as providing an upper bound on the overall level of 14C depletion at any marine site then, for the more equatorial locations, these are encapsulated in Marine20’s 2
${\rm{\Delta }}{R^{LSG}}$
-adjusted) GS scenario estimates (dashed lines) as providing an upper bound on the overall level of 14C depletion at any marine site then, for the more equatorial locations, these are encapsulated in Marine20’s 2
![]() $\sigma $
uncertainty bands (shaded gray). Only once we extend beyond approximately 40ºS or 40ºN do the (
$\sigma $
uncertainty bands (shaded gray). Only once we extend beyond approximately 40ºS or 40ºN do the (
![]() ${\rm{\Delta }}{R^{LSG}}$
-adjusted) GS scenario of the LSG OGCM provide location-specific estimates of overall MRA that are not covered by the tail estimates one would obtain with (a
${\rm{\Delta }}{R^{LSG}}$
-adjusted) GS scenario of the LSG OGCM provide location-specific estimates of overall MRA that are not covered by the tail estimates one would obtain with (a
![]() ${\rm{\Delta }}{R_{20}}$
-adjusted) Marine20. This suggests that on our transects, for calibration of marine samples from regions within ∼ 40ºS–40ºN, the use of Marine20 (with a modern day
${\rm{\Delta }}{R_{20}}$
-adjusted) Marine20. This suggests that on our transects, for calibration of marine samples from regions within ∼ 40ºS–40ºN, the use of Marine20 (with a modern day
![]() ${\rm{\Delta }}{R_{20}}$
) can be justified back to 55,000 cal yr BP as its inbuilt uncertainty will cover the upper (GS-scenario) limit for regional 14C depletion. However, at higher latitudes, the GS scenarios indicate the possibility of substantial additional localized 14C oceanic depletion during glacial periods that is not captured in the global scale Marine20. Under the GS scenario, along our transects, the overall MRA in high-latitude polar regions may be increased by up to 1000 14C yrs during the glacial compared to the global Marine20 values. To recreate this GS scenario, these polar-specific increases would need to be accounted for by a corresponding change to
${\rm{\Delta }}{R_{20}}$
) can be justified back to 55,000 cal yr BP as its inbuilt uncertainty will cover the upper (GS-scenario) limit for regional 14C depletion. However, at higher latitudes, the GS scenarios indicate the possibility of substantial additional localized 14C oceanic depletion during glacial periods that is not captured in the global scale Marine20. Under the GS scenario, along our transects, the overall MRA in high-latitude polar regions may be increased by up to 1000 14C yrs during the glacial compared to the global Marine20 values. To recreate this GS scenario, these polar-specific increases would need to be accounted for by a corresponding change to
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
if Marine20 is used for calibration.
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
if Marine20 is used for calibration.
Fourthly, Figure 3 suggests that from 40,000–11,500 cal yr BP the increase in a particular location from the Marine20-based estimate of overall MRA to the LSG OGCM under its GS scenario (after the initial
![]() ${\rm{\Delta }}{R_{20}}$
and
${\rm{\Delta }}{R_{20}}$
and
![]() $\Delta {R^{LSG}}$
adjustments) is approximately constant over time. This can be seen very clearly in Figure S1 of the Supplementary Information B where we present the increase for each location along our three selected ocean transects. For a given location, we can therefore get a good approximation of the overall MRA estimate under the GS scenario of the LSG OGCM (at least between 40,000–11,500 cal yr BP) with Marine20 by applying a constant (albeit location-specific) increase to
$\Delta {R^{LSG}}$
adjustments) is approximately constant over time. This can be seen very clearly in Figure S1 of the Supplementary Information B where we present the increase for each location along our three selected ocean transects. For a given location, we can therefore get a good approximation of the overall MRA estimate under the GS scenario of the LSG OGCM (at least between 40,000–11,500 cal yr BP) with Marine20 by applying a constant (albeit location-specific) increase to
![]() ${\rm{\Delta }}{R_{20}}$
. These increases (latitudinally averaged rather than along single transects) will become our
${\rm{\Delta }}{R_{20}}$
. These increases (latitudinally averaged rather than along single transects) will become our
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
.
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
.
3 Adjustments to Recreate a Glacial LSG OGCM Scenario Using Marine20 from 55,000–11,500 cal yr BP
3.1 Summarizing the High-Latitude Increases in Regional 14C Depletion for a Glacial Scenario
To provide an upper (maximum) bound on the additional regional 14C depletion that may need to be incorporated into Marine20’s
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
at high-latitudes during glacial periods, we have calculated latitudinal-average
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
at high-latitudes during glacial periods, we have calculated latitudinal-average
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
adjustments. These adjustments take the form described in Section 2 where, for every marine location on the 2.5º by 2.5º grid of the LSG OGCM grid, we have:
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
adjustments. These adjustments take the form described in Section 2 where, for every marine location on the 2.5º by 2.5º grid of the LSG OGCM grid, we have:
-
Shifted the LSG OGCM estimates so that the PD scenario in that location has a mean during the period from 11,500–0 cal yr BP that matches Marine20’s
 $R_{20}^{GlobalAv}\left( \theta \right)$
.
$R_{20}^{GlobalAv}\left( \theta \right)$
. -
Calculated the difference in the mean, during the glacial period from 40,000–11,500 cal yr BP, between
 $R_{20}^{GlobalAv}\left( \theta \right)$
and the (shifted) GS scenario.
$R_{20}^{GlobalAv}\left( \theta \right)$
and the (shifted) GS scenario.
This difference indicates by how much the level of 14C depletion must be increased from the global-only
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
to recreate the regional GS scenario of the LSG OGCM. At a given latitude, we summarize the mean (and 95% quantiles) of these increases to obtain the latitude-dependent
$R_{20}^{GlobalAv}\left( \theta \right)$
to recreate the regional GS scenario of the LSG OGCM. At a given latitude, we summarize the mean (and 95% quantiles) of these increases to obtain the latitude-dependent
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
values shown in Figure 1 (and Figure 4 showing the adjustment required at a particular latitude).
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
values shown in Figure 1 (and Figure 4 showing the adjustment required at a particular latitude).

Figure 4 The latitudinal-average increase
![]() $\Delta R_\;^{Hol\; \to \;GS}\;$
needed to recreate the GS scenario of the LSG OGCM from Marine20 during the glacial time period (reproducing earlier Figure 1). To estimate the adjustment needed at a particular location, e.g., core site MD02-2496 at 49ºN, we read the value for the corresponding latitude. Here, the required boost
$\Delta R_\;^{Hol\; \to \;GS}\;$
needed to recreate the GS scenario of the LSG OGCM from Marine20 during the glacial time period (reproducing earlier Figure 1). To estimate the adjustment needed at a particular location, e.g., core site MD02-2496 at 49ºN, we read the value for the corresponding latitude. Here, the required boost
![]() $\Delta R_{MD02 - 2496}^{Hol\; \to \;GS}$
to recreate the GS scenario using Marine20 (to be added to an initial Holocene
$\Delta R_{MD02 - 2496}^{Hol\; \to \;GS}$
to recreate the GS scenario using Marine20 (to be added to an initial Holocene
![]() $\Delta R_{20\;}^{Hol}$
estimate) is ca. 390 14C yrs.
$\Delta R_{20\;}^{Hol}$
estimate) is ca. 390 14C yrs.
Note that we perform latitudinal averaging, rather than providing latitude and longitude dependent adjustments, to reduce the effect of model specificity in the LSG OGCM estimates regarding precise sea-ice location/dynamics and freshwater balance. We also do not provide, or suggest using, the variance on the shifts at a given latitude. The set of modeled values provided by the LSG OGCM at a given latitude are not well approximated by a normal distribution. To recreate the GS scenario, we propose simply applying the mean shift
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
at a given latitude and leaving the uncertainty as for the Holocene-based
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
at a given latitude and leaving the uncertainty as for the Holocene-based
![]() ${\rm{\Delta }}{R_{20}}$
.
${\rm{\Delta }}{R_{20}}$
.
We also calculate the shift needed based on the period from 40,000–11,500 cal yr BP, to avoid the non-constancy in the differences from the LSG OGCM outputs to Marine20 at high latitudes from 55,000–40,000 cal yrs BP when atmospheric 14C levels increased very rapidly (Reimer et al. Reference Reimer, Austin, Bard, Bayliss, Blackwell, Ramsey, Butzin, Cheng, Edwards and Friedrich2020). We suggest our calculated shifts can however be applied back to 55,000 cal yr BP, although at very high latitudes, users should recognize additional adjustments may be needed for 14C samples of such great age.
For more equatorial ocean locations, the increase
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
is seen to overlap with the uncertainty bands on
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
is seen to overlap with the uncertainty bands on
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
. For these low-latitude regions, within ca. 40ºS–40ºN, we therefore suggest that no artificial boosting of (a Holocene-based)
$R_{20}^{GlobalAv}\left( \theta \right)$
. For these low-latitude regions, within ca. 40ºS–40ºN, we therefore suggest that no artificial boosting of (a Holocene-based)
![]() ${\rm{\Delta }}{R_{20}}$
in glacial periods is required. A user can (cautiously) calibrate 14C samples into the glacial period using an estimate of
${\rm{\Delta }}{R_{20}}$
in glacial periods is required. A user can (cautiously) calibrate 14C samples into the glacial period using an estimate of
![]() ${\rm{\Delta }}{R_{20}}$
from the recent past. Outside these regions, at higher latitudes, the boosting needed to represent the GS scenario of the LSG OGCM increases rapidly.
${\rm{\Delta }}{R_{20}}$
from the recent past. Outside these regions, at higher latitudes, the boosting needed to represent the GS scenario of the LSG OGCM increases rapidly.
The boost
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
does not however increase monotonically with latitude: it rises to a maximum around 60ºS/70ºN but then drops at the very poles. This is perhaps understandable since the greatest glacial boost will be needed when the local oceanic conditions in the GS scenario have changed most substantially from those seen in the Holocene/PD scenario. This occurs not at the poles themselves (where both the PD and GS scenarios have sea-ice) but rather slightly below the poles (where the GS scenario has sea-ice, but the PD does not). The extent of sea-ice in the different LSG OGCM scenarios can be found in Figures 3 and 10 of Butzin et al. (Reference Butzin, Prange and Lohmann2005). At its greatest, around 60ºS and 70ºN, the GS scenario of the LSG OGCM suggests that glacial period
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
does not however increase monotonically with latitude: it rises to a maximum around 60ºS/70ºN but then drops at the very poles. This is perhaps understandable since the greatest glacial boost will be needed when the local oceanic conditions in the GS scenario have changed most substantially from those seen in the Holocene/PD scenario. This occurs not at the poles themselves (where both the PD and GS scenarios have sea-ice) but rather slightly below the poles (where the GS scenario has sea-ice, but the PD does not). The extent of sea-ice in the different LSG OGCM scenarios can be found in Figures 3 and 10 of Butzin et al. (Reference Butzin, Prange and Lohmann2005). At its greatest, around 60ºS and 70ºN, the GS scenario of the LSG OGCM suggests that glacial period
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
may be 1000 to 1500 14C yrs greater than in the recent past. If we fail to recognize the potential for such an increase in polar depletion when calibrating such high latitude samples against Marine20, then we may obtain calibrated ages that are ca. 1000 cal yrs too old.
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
may be 1000 to 1500 14C yrs greater than in the recent past. If we fail to recognize the potential for such an increase in polar depletion when calibrating such high latitude samples against Marine20, then we may obtain calibrated ages that are ca. 1000 cal yrs too old.
An equivalent investigation of the changes required to a modern-day
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
to recreate the more extreme CS scenario of the LSG OGCM, while still using Marine20, can be found in the Supplementary Information C (Figures S3–S6). As for the GS scenario, the differences in modeled MRA between Marine20 and the CS scenario remain approximately constant over time, at least from 40,000–11,500 cal yr BP, at a given location. We can therefore obtain an approximate CS scenario with Marine20 by applying a constant, latitude-dependent, boost
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
to recreate the more extreme CS scenario of the LSG OGCM, while still using Marine20, can be found in the Supplementary Information C (Figures S3–S6). As for the GS scenario, the differences in modeled MRA between Marine20 and the CS scenario remain approximately constant over time, at least from 40,000–11,500 cal yr BP, at a given location. We can therefore obtain an approximate CS scenario with Marine20 by applying a constant, latitude-dependent, boost
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;CS}$
to a modern-day
${\rm{\Delta }}R_{20}^{Hol\; \to \;CS}$
to a modern-day
![]() ${\rm{\Delta }}{R_{20}}$
estimate (Figure S5). The latitudinal
${\rm{\Delta }}{R_{20}}$
estimate (Figure S5). The latitudinal
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;CS}$
shifts needed to be applied to recreate the CS scenario from Marine20 are, as expected, somewhat larger than the shifts required to recreate the GS scenario (Table A2, Appendix). A user wishing to be more cautious in calibration of samples during the glacial period may choose to select an upper bound for the polar 14C depletion using this CS scenario.
${\rm{\Delta }}R_{20}^{Hol\; \to \;CS}$
shifts needed to be applied to recreate the CS scenario from Marine20 are, as expected, somewhat larger than the shifts required to recreate the GS scenario (Table A2, Appendix). A user wishing to be more cautious in calibration of samples during the glacial period may choose to select an upper bound for the polar 14C depletion using this CS scenario.
3.2 Comparison with Independent Estimates of Surface MRA over Time
To provide an independent assessment of our proposed bracketing approach, we provide an illustration of the high- and low- depletion estimates of the overall MRA,
![]() ${\rm{R}}_{20}^{{\rm{Location}}}\left( {\rm{\theta }} \right)$
, that we would obtain from 40,000–0 cal yr BP at the location of deep-sea core MD04-2829 (59.0ºN, 9.5ºW; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019). This is a high-latitude site (59ºN) within the Northern Atlantic where we might expect additional, localised, variations in
${\rm{R}}_{20}^{{\rm{Location}}}\left( {\rm{\theta }} \right)$
, that we would obtain from 40,000–0 cal yr BP at the location of deep-sea core MD04-2829 (59.0ºN, 9.5ºW; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019). This is a high-latitude site (59ºN) within the Northern Atlantic where we might expect additional, localised, variations in
![]() ${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
during the glacial period. We then compare our suggested bounding 14C depletion scenarios against estimates of surface MRA obtained directly from this core’s planktonic 14C measurements. MD04-2829 has a calendar age-depth timescale based upon the alignment of changes in the abundance of planktonic foraminifer species N. pachyderma to the NGRIP δ18O ice record (Svensson et al. Reference Svensson, Andersen, Bigler, Clausen, Dahl-Jensen, Davies, Johnsen, Muscheler, Parrenin, Rasmussen, Röthlisberger, Seierstad, Steffensen and Vinther2008). Measurements of planktic 14C within the core can therefore be compared against IntCal20 to provide independent, and direct, estimates of the overall surface-atmospheric MRA.
${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
during the glacial period. We then compare our suggested bounding 14C depletion scenarios against estimates of surface MRA obtained directly from this core’s planktonic 14C measurements. MD04-2829 has a calendar age-depth timescale based upon the alignment of changes in the abundance of planktonic foraminifer species N. pachyderma to the NGRIP δ18O ice record (Svensson et al. Reference Svensson, Andersen, Bigler, Clausen, Dahl-Jensen, Davies, Johnsen, Muscheler, Parrenin, Rasmussen, Röthlisberger, Seierstad, Steffensen and Vinther2008). Measurements of planktic 14C within the core can therefore be compared against IntCal20 to provide independent, and direct, estimates of the overall surface-atmospheric MRA.
Our bracketed estimates for
![]() $R_{20}^{Location}\left( \theta \right)$
are based on adjusting the global-scale
$R_{20}^{Location}\left( \theta \right)$
are based on adjusting the global-scale
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
of Marine20, just as would be implemented by a user of our approach. We first estimate a
$R_{20}^{GlobalAv}\left( \theta \right)$
of Marine20, just as would be implemented by a user of our approach. We first estimate a
![]() ${\rm{\Delta }}R_{20}^{Hol}$
based upon the single most recent 14C measurement within the MD04-2829 core. When combined with Marine20’s
${\rm{\Delta }}R_{20}^{Hol}$
based upon the single most recent 14C measurement within the MD04-2829 core. When combined with Marine20’s
![]() $R_{20}^{GlobalAv}\left( \theta \right),\;$
this
$R_{20}^{GlobalAv}\left( \theta \right),\;$
this
![]() ${\rm{\Delta }}R_{20}^{Hol}$
fixes the estimate for the overall MRA throughout the Holocene and determines the lower bound for the overall depletion in the glacial period. The resultant Holocene, and low-depletion glacial, estimate for
${\rm{\Delta }}R_{20}^{Hol}$
fixes the estimate for the overall MRA throughout the Holocene and determines the lower bound for the overall depletion in the glacial period. The resultant Holocene, and low-depletion glacial, estimate for
![]() $\;R_{20}^{Location}\left( \theta \right)$
is plotted in blue (with 1
$\;R_{20}^{Location}\left( \theta \right)$
is plotted in blue (with 1
![]() ${\rm{\sigma }}$
intervals). The location-specific upper bound for the glacial period is then calculated by applying the appropriate latitudinal shift
${\rm{\sigma }}$
intervals). The location-specific upper bound for the glacial period is then calculated by applying the appropriate latitudinal shift
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
. In the case of MD04-2829 (at 59ºN) this is 1000 14C yrs (see Table A2, Appendix). These shifted upper-bound glacial estimates are shown in red (with 1
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
. In the case of MD04-2829 (at 59ºN) this is 1000 14C yrs (see Table A2, Appendix). These shifted upper-bound glacial estimates are shown in red (with 1
![]() ${\rm{\sigma }}$
intervals).
${\rm{\sigma }}$
intervals).
We would hope that the directly observed MRA estimates obtained from planktonic 14C measurements within the core (shown as black dots, with 1
![]() ${\rm{\sigma }}$
intervals) would lie between the two bounding (high- and low-)
${\rm{\sigma }}$
intervals) would lie between the two bounding (high- and low-)
![]() $R_{20}^{Location}\left( \theta \right)$
curves. Figure 5 shows this to generally be the case. We note that, during the Holocene, the blue
$R_{20}^{Location}\left( \theta \right)$
curves. Figure 5 shows this to generally be the case. We note that, during the Holocene, the blue
![]() ${\rm{\Delta }}R_{20}^{Hol}$
-adjusted estimate appears a good fit. This suggests that Marine20’s
${\rm{\Delta }}R_{20}^{Hol}$
-adjusted estimate appears a good fit. This suggests that Marine20’s
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
is capturing the main global-scale effects on the MRA; and that temporal variations in
$R_{20}^{GlobalAv}\left( \theta \right)$
is capturing the main global-scale effects on the MRA; and that temporal variations in
![]() ${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
are small during the Holocene (even at high latitudes). This supports our recommendation that, even at high-latitudes, users can continue using Marine20 (with a constant
${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
are small during the Holocene (even at high latitudes). This supports our recommendation that, even at high-latitudes, users can continue using Marine20 (with a constant
![]() ${\rm{\Delta }}R_{20}^\;$
) during the Holocene.
${\rm{\Delta }}R_{20}^\;$
) during the Holocene.

Figure 5 Plot of the upper and lower bounds on the overall MRA,
![]() $R_{20}^{Location}\left( \theta \right)$
obtained using our proposed bracketing approach compared against estimates of MRA calculated directly from planktic foraminifera (black dots) in the deep-sea core (MD04-2829, 59ºN 9ºW; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019). The high (red) and low (blue) depletion estimates shown are calculated by applying the appropriate latitudinal-shift to the global-scale
$R_{20}^{Location}\left( \theta \right)$
obtained using our proposed bracketing approach compared against estimates of MRA calculated directly from planktic foraminifera (black dots) in the deep-sea core (MD04-2829, 59ºN 9ºW; Skinner et al. Reference Skinner, Muschitiello and Scrivner2019). The high (red) and low (blue) depletion estimates shown are calculated by applying the appropriate latitudinal-shift to the global-scale
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
of Marine20. Both the curves and the observations are shown with 1
$R_{20}^{GlobalAv}\left( \theta \right)$
of Marine20. Both the curves and the observations are shown with 1
![]() $\sigma $
intervals. Heinrich events are overlain as shaded intervals.
$\sigma $
intervals. Heinrich events are overlain as shaded intervals.
Once we enter the glacial period however, we see that the observed MRAs in our high-latitude location vary significantly away from the low-depletion scenario. There are periods when
![]() ${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
has clearly increased substantially in this polar marine location, and calibrating using the low-depletion scenario would not be appropriate. However, the directly observed estimates still lie within the upper- and lower-depletion curves, indicating that our bracketing approach is able to bound the variability in
${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
has clearly increased substantially in this polar marine location, and calibrating using the low-depletion scenario would not be appropriate. However, the directly observed estimates still lie within the upper- and lower-depletion curves, indicating that our bracketing approach is able to bound the variability in
![]() ${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
. As might be expected for a North Atlantic core such as MD04-2829, the regional
${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
. As might be expected for a North Atlantic core such as MD04-2829, the regional
![]() ${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
appears to increase during/around the Heinrich events and around the LGM with the overall MRA moving towards its upper (red) limits, and then reduce away from these periods dropping back towards the lower (blue) limit.
${\rm{\Delta }}R_{20}^\;\left( \theta \right)$
appears to increase during/around the Heinrich events and around the LGM with the overall MRA moving towards its upper (red) limits, and then reduce away from these periods dropping back towards the lower (blue) limit.
4 Polar Calibration Examples (Offshore Vancouver Island 49ºN, 127ºW)
For our worked examples, we will consider the deep-sea core MD02-2496, sited offshore of Vancouver Island, Western Canada (Cosma et al. Reference Cosma, Hendy and Chang2008; Taylor et al. Reference Taylor, Hendy and Pak2014). This core is located at 48°58′47″N, 127°02′14″W and at 1243 m water depth. It contains a 38.38-m-long sequence of glaciomarine and hemipelagic sediments with 46 14C dates provided along the core. Two of these measurements lack depth information and so are not considered, and four have been removed as they are only reported as being greater than a certain 14C yr BP. We will use the remaining 40 14C dates to illustrate the calibration of individual 14C samples, and the creation of an age-depth model that combines all the data. OxCal code is provided in Supplementary Information E (single sample calibration) and F (age-depth model).
The location of core MD02-2496 has remained ice-sheet free, with the maximal extent of the Cordilleran ice sheet occurring around 18–19.5 cal kyr BP. However, we note that the proximity of this former ice sheet does complicate the issue of changes in
![]() ${\rm{\Delta }}R\left( \theta \right)$
due to glacio-isostatic adjustments. Various sites along the British Columbia coast have had quite different sea level histories (Clague and James Reference Clague and James2002). Such changes at a marine site may cause further changes to
${\rm{\Delta }}R\left( \theta \right)$
due to glacio-isostatic adjustments. Various sites along the British Columbia coast have had quite different sea level histories (Clague and James Reference Clague and James2002). Such changes at a marine site may cause further changes to
![]() ${\rm{\Delta }}R\left( \theta \right)$
over time.
${\rm{\Delta }}R\left( \theta \right)$
over time.
For this site, we can estimate a modern-day value of
![]() ${\rm{\Delta }}{R_{20}}$
based on samples from the recent past taken from http://calib.org/marine/, see Figure 6. The database contains eight samples from near the site of core MD02-2496. We discount the sample in David Channel (MapNo 949) as it relates to a deposit feeding organism (indicated by the red pushpin) and lies in a channel rather than open ocean. Using the remaining seven samples, we obtain an estimate for a modern-day value of
${\rm{\Delta }}{R_{20}}$
based on samples from the recent past taken from http://calib.org/marine/, see Figure 6. The database contains eight samples from near the site of core MD02-2496. We discount the sample in David Channel (MapNo 949) as it relates to a deposit feeding organism (indicated by the red pushpin) and lies in a channel rather than open ocean. Using the remaining seven samples, we obtain an estimate for a modern-day value of
![]() ${\rm{\Delta }}{R_{20}} = \;178 \pm 73$
14C yrs (1
${\rm{\Delta }}{R_{20}} = \;178 \pm 73$
14C yrs (1
![]() $\sigma )$
using the online marine reservoir correction database tool (Reimer and Reimer Reference Reimer and Reimer2001).
$\sigma )$
using the online marine reservoir correction database tool (Reimer and Reimer Reference Reimer and Reimer2001).

Figure 6 Location of 14C samples near sire MD02-2496 taken from the marine radiocarbon reservoir database (http://calib.org/marine/). We use the seven (modern-day) ticked samples to estimate a modern day
![]() $\Delta {R_{20}}$
for the site. We do not use MapNo 949 since this corresponds to a deposit-feeding organism (red pushpin) and lies in David Channel rather than the open ocean. Credit: Map data ©2021 GeoBasis-DE/BKG, Google Imagery ©2021 Terrametrics.
$\Delta {R_{20}}$
for the site. We do not use MapNo 949 since this corresponds to a deposit-feeding organism (red pushpin) and lies in David Channel rather than the open ocean. Credit: Map data ©2021 GeoBasis-DE/BKG, Google Imagery ©2021 Terrametrics.
4.1 Calibration of Single 14C Samples from Polar Regions
Suppose we wish to calibrate two individual 14C samples taken from the deep-sea core site MD02-2496 at 49.0ºN, 127.0ºW:
-
1. Holocene Sample A (at depth 412 cm) with a 14C age of 9215 ± 25 14C yrs BP (1
 $\sigma )$
$\sigma )$
-
2. Glacial Sample B (at depth 2057cm) with a 14C age of 25190 ± 150 14C yrs BP (1
 $\sigma )$
$\sigma )$
Readers should note that these examples of individual calibration are intended as illustrations only. In practice, we would always suggest calibrating 14C samples within a core together as part of an age-depth model rather than individually. By calibrating jointly, we can usually add strength to our calendar age estimation.
4.1.1 Calibration during the Holocene (9215 ± 25 14C yrs BP—Sample A)
Since the marine 14C sample (sample A) that we wish to calibrate is from the Holocene, we do not need to incorporate a glacial increase in localized depletion. We can therefore calibrate the 14C determination directly against Marine20 with the single value of
![]() ${\rm{\Delta }}{R_{20}}$
calculated from the (recent past) samples shown in Figure 6. This calibration is shown in Figure 7 and provides a mean calibrated age estimate of 9570 cal yr BP, with a 95.4% confidence interval of [9340, 9840] cal yr BP.
${\rm{\Delta }}{R_{20}}$
calculated from the (recent past) samples shown in Figure 6. This calibration is shown in Figure 7 and provides a mean calibrated age estimate of 9570 cal yr BP, with a 95.4% confidence interval of [9340, 9840] cal yr BP.

Figure 7 Calibration of marine sample A from the Holocene (9215 ± 25 14C yrs BP) taken from deep-sea core MD02-2496 (ca. 49.0ºN, 127.0ºW). We use a value of
![]() $\Delta {R_{20}} = \;178 \pm 73$
14C yrs. Calibration is performed using OxCal v4.4.4 (Bronk Ramsey Reference Bronk Ramsey2009) using the Marine20 calibration curve (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020). The Gaussian curves on the y-axis represent the raw 14C-age (lighter) and the
$\Delta {R_{20}} = \;178 \pm 73$
14C yrs. Calibration is performed using OxCal v4.4.4 (Bronk Ramsey Reference Bronk Ramsey2009) using the Marine20 calibration curve (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020). The Gaussian curves on the y-axis represent the raw 14C-age (lighter) and the
![]() $\Delta {R_{20}}$
-adjusted 14C-age (darker) of the marine sample. We calibrate the
$\Delta {R_{20}}$
-adjusted 14C-age (darker) of the marine sample. We calibrate the
![]() $\Delta {R_{20}}$
-adjusted 14C-age against the Marine20 curve. The posterior calendar age estimate is shown along the x-axis. Note that, the OxCal calendar age scale runs from left (oldest) to right (youngest/more recent).
$\Delta {R_{20}}$
-adjusted 14C-age against the Marine20 curve. The posterior calendar age estimate is shown along the x-axis. Note that, the OxCal calendar age scale runs from left (oldest) to right (youngest/more recent).
Note that we can be confident that Sample A arises from the Holocene as the 95.4% calendar age range obtained under the calibration does not extend into the glacial. If the calendar age interval did extend beyond 11,500 cal yr BP, then we would advise that the dual approach of Section 4.1.2 is required.
4.1.2 Calibration during the Glacial (25190 ± 150 14C yrs BP—Sample B)
To calibrate a sample from the glacial period at the site of core MD02-2496, we must first calculate the increase, from the Holocene/recent-past
![]() ${\rm{\Delta }}{R_{20}}$
, that is required to emulate the GS scenario of the LSG OGCM. At a latitude of 49ºN, Figure 4 and Table A2 suggests an increase of 390 14C yrs is needed. We then calibrate against Marine20 under two different glacial scenarios. We hope these scenarios will bracket the 14C depletion at the deep-sea site and time of the sample.
${\rm{\Delta }}{R_{20}}$
, that is required to emulate the GS scenario of the LSG OGCM. At a latitude of 49ºN, Figure 4 and Table A2 suggests an increase of 390 14C yrs is needed. We then calibrate against Marine20 under two different glacial scenarios. We hope these scenarios will bracket the 14C depletion at the deep-sea site and time of the sample.
Calibrating in a low-depletion glacial scenario (oldest calendar age limit): To estimate the calendar age of the MD02-2496 14C determination (
![]() $25,\!190 \pm 150$
14C yrs BP) in a low-depletion glacial scenario, we calibrate against Marine20 using the level of regional 14C depletion seen in the present day, i.e.,
$25,\!190 \pm 150$
14C yrs BP) in a low-depletion glacial scenario, we calibrate against Marine20 using the level of regional 14C depletion seen in the present day, i.e.,
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{Hol} = {\rm{\Delta }}{R_{20}} = 178\; \pm 73$
14C yrs. This calibration still incorporates global-scale glacial conditions (e.g., the increase in 14C concentrations, changes in CO2, and large-scale carbon cycle changes over the Holocene/pre-Holocene boundary that is included in Marine20) but does not incorporate the potential for regional sea-ice to temporally affect the site-specific
${\rm{\Delta }}R_{MD02 - 2496}^{Hol} = {\rm{\Delta }}{R_{20}} = 178\; \pm 73$
14C yrs. This calibration still incorporates global-scale glacial conditions (e.g., the increase in 14C concentrations, changes in CO2, and large-scale carbon cycle changes over the Holocene/pre-Holocene boundary that is included in Marine20) but does not incorporate the potential for regional sea-ice to temporally affect the site-specific
![]() ${\rm{\Delta }}{R_{20}}\left( \theta \right)$
.
${\rm{\Delta }}{R_{20}}\left( \theta \right)$
.
Calibrating in a high-depletion glacial scenario (youngest calendar age limit): To calibrate in a high-depletion scenario that assumes regional/localized polar conditions similar to those modeled in the GS scenario of the LSG OGCM, we add our latitudinal boost
![]() ${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
to the modern-day estimate of
${\rm{\Delta }}R_{20}^{Hol\; \to \;GS}$
to the modern-day estimate of
![]() ${\rm{\Delta }}{R_{20}}$
:
${\rm{\Delta }}{R_{20}}$
:
We retain the same (
![]() $1\sigma )$
uncertainty of ± 73 14C yrs taken from the value of
$1\sigma )$
uncertainty of ± 73 14C yrs taken from the value of
![]() ${\rm{\Delta }}{R_{20}}$
. We then calibrate against Marine20 with this boosted
${\rm{\Delta }}{R_{20}}$
. We then calibrate against Marine20 with this boosted
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{GS}$
estimate of regional depletion.
${\rm{\Delta }}R_{MD02 - 2496}^{GS}$
estimate of regional depletion.
Obtaining bracketing calendar ages: The calendar age estimates obtained from calibrating the glacial sample (
![]() $25,\!190 \pm 150$
14C yrs BP) with the bracketing low- and high-depletion scenarios are shown in Figure 8 and Table 1. The overall calibrated age range covering both limiting depletion scenarios (running from the overall minimum calendar age to the maximum calendar age) is [27560, 28750] cal yr BP (Table 1). This combined interval aims to cover the maximum potential calendar age range for the 14C sample. If we expect the true value of regional depletion
$25,\!190 \pm 150$
14C yrs BP) with the bracketing low- and high-depletion scenarios are shown in Figure 8 and Table 1. The overall calibrated age range covering both limiting depletion scenarios (running from the overall minimum calendar age to the maximum calendar age) is [27560, 28750] cal yr BP (Table 1). This combined interval aims to cover the maximum potential calendar age range for the 14C sample. If we expect the true value of regional depletion
![]() ${\rm{\Delta }}R\left( \theta \right)$
at the time the sample was exchanging with its environment to lie somewhere between the two extreme low- and high-depletion scenarios, the calendar age of the sample will also lie between the two scenario estimates. If no external knowledge is available regarding whether the low- or high- depletion glacial scenario is more appropriate for the sample, this extremely broad bracketing may be all we can provide. However, if independent information on the extent of sea-ice in the location is available, a calibration user may wish to make an argument that either the low- or high-depletion calibration scenarios (and hence calibrated ages) are more appropriate (or indeed argue for an intermediate level of depletion).
${\rm{\Delta }}R\left( \theta \right)$
at the time the sample was exchanging with its environment to lie somewhere between the two extreme low- and high-depletion scenarios, the calendar age of the sample will also lie between the two scenario estimates. If no external knowledge is available regarding whether the low- or high- depletion glacial scenario is more appropriate for the sample, this extremely broad bracketing may be all we can provide. However, if independent information on the extent of sea-ice in the location is available, a calibration user may wish to make an argument that either the low- or high-depletion calibration scenarios (and hence calibrated ages) are more appropriate (or indeed argue for an intermediate level of depletion).

Figure 8 Calibration of glacial sample B with a 14C determination of
![]() $25,\!190 \pm 150$
14C yrs BP from deep-sea core MD02-2496 (49ºN 127ºW). The top distribution shows the calibrated age under a low-depletion marine scenario (no additional changes in 14C depletion over those seen in Equatorial waters). The bottom plot, the calibrated age under a high-depletion polar scenario (intended to represent conditions similar to the LGM). Note that the low-depletion glacial scenario (top) provides an older calendar age estimate—the OxCal calendar age scale runs from left (oldest) to right (youngest/more recent).
$25,\!190 \pm 150$
14C yrs BP from deep-sea core MD02-2496 (49ºN 127ºW). The top distribution shows the calibrated age under a low-depletion marine scenario (no additional changes in 14C depletion over those seen in Equatorial waters). The bottom plot, the calibrated age under a high-depletion polar scenario (intended to represent conditions similar to the LGM). Note that the low-depletion glacial scenario (top) provides an older calendar age estimate—the OxCal calendar age scale runs from left (oldest) to right (youngest/more recent).
Table 1 95.4% credible intervals for the calendar age of sample B (a glacial-period marine 14C sample with a 14C determination of
![]() $25,\!190 \pm 150$
14C yrs BP) from core MD02-2496 (∼49ºN) under a low- and high-depletion glacial scenario.
$25,\!190 \pm 150$
14C yrs BP) from core MD02-2496 (∼49ºN) under a low- and high-depletion glacial scenario.

We stress that the combined (bracketed) interval of [27560, 28750] cal yr BP should have a coverage that is considerably greater than 95.4% (since it covers the two extremes). However, we do not provide any probability distribution on it, and no such distribution should be inferred as we expect that the true level of 14C depletion may transition relatively rapidly between scenarios (spending less time at intermediate values) as sea-ice appears and disappears. Additionally, while in principle, there is no guarantee that the 95.4% quantiles for the calibrated age of a 14C date decrease monotonically with increasing MRA/depletion levels (i.e., there might be an intermediate level of depletion which has 95.4% calendar age quantiles outside the range above) in practice, due to the smoothness of the current Marine20 estimate, there are no such cases pre-Holocene.
4.2 Calibrating Multiple 14C Polar Determinations and Age Modeling
Polar 14C calibration is also required when creating age-depth models for sediment cores based upon multiple 14C determinations (e.g., McClymont et al. Reference McClymont, Bentley, Hodgson, Spencer-Jones, Wardley, West, Croudace, Berg, Gröcke, Kuhn, Jamieson, Sime and Phillips2022; Taylor et al. Reference Taylor, Hendy and Pak2014). For such age-depth models, 14C calibration is typically done internally to the creation of the chronology. We recommend an analogous approach to that of Section 4.1. For those Holocene 14C samples that are used to inform the overall chronology, we suggest a user apply a single
![]() ${\rm{\Delta }}R_{20}^{Hol}$
; while for older samples we suggest creating separate age-depth models under the low- and high-depletion scenarios. Then, when estimating the age at any specific depth, a user can read off the calendar age estimate for each age-depth model (low- and high-depletion) and use the same bracketing approach described in Section 4.1.2. Alternatively, they may wish to use independent palaeoclimatic/proxy evidence to support an age-depth model based on the level of 14C depletion under one scenario (or to justify an intermediate level of depletion). As for the calibration of single 14C samples, this can all be achieved within standard calibration software simply by adjusting, e.g., DeltaR, during age-depth model construction (see Supplementary Information F).
${\rm{\Delta }}R_{20}^{Hol}$
; while for older samples we suggest creating separate age-depth models under the low- and high-depletion scenarios. Then, when estimating the age at any specific depth, a user can read off the calendar age estimate for each age-depth model (low- and high-depletion) and use the same bracketing approach described in Section 4.1.2. Alternatively, they may wish to use independent palaeoclimatic/proxy evidence to support an age-depth model based on the level of 14C depletion under one scenario (or to justify an intermediate level of depletion). As for the calibration of single 14C samples, this can all be achieved within standard calibration software simply by adjusting, e.g., DeltaR, during age-depth model construction (see Supplementary Information F).
We consider an age-depth model fitted to the 40 14C determinations in core MD02-2496 using OxCal’s p-sequence (Bronk Ramsey Reference Bronk Ramsey2008; Bronk Ramsey and Lee Reference Bronk Ramsey and Lee2013). To create this model, we have averaged the two measurements (9215 ± 25 and 10,065 ± 45 14C yrs BP) at 412cm into a single 14C date of 9415 ± 22 14C yrs BP. For the low-depletion glacial scenario, we use a regional correction of
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{Hol} = 178\; \pm 73{\rm{\;}}$
14C yrs as justified in the previous section; while for the high-depletion glacial scenario, we use a
${\rm{\Delta }}R_{MD02 - 2496}^{Hol} = 178\; \pm 73{\rm{\;}}$
14C yrs as justified in the previous section; while for the high-depletion glacial scenario, we use a
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{GS} = 568 \pm 73$
14C yrs. In this location, the transition between the Holocene and glacial corresponds to approximately 10,000 14C yrs BP, i.e., a sample with a determination of 10,000 14C yrs BP calibrates to being just older than 11,500 cal yr BP using a non-glacial
${\rm{\Delta }}R_{MD02 - 2496}^{GS} = 568 \pm 73$
14C yrs. In this location, the transition between the Holocene and glacial corresponds to approximately 10,000 14C yrs BP, i.e., a sample with a determination of 10,000 14C yrs BP calibrates to being just older than 11,500 cal yr BP using a non-glacial
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{Hol} = 178\; \pm 73{\rm{\;}}$
14C yrs. For both our high and low-depletion age-depth models, we therefore apply a Holocene value of
${\rm{\Delta }}R_{MD02 - 2496}^{Hol} = 178\; \pm 73{\rm{\;}}$
14C yrs. For both our high and low-depletion age-depth models, we therefore apply a Holocene value of
![]() ${\rm{\Delta }}R\left( \theta \right)$
when constructing the age-depth model for all 14C samples at depths from 0–412 cm. Deeper in the core, we apply the appropriate high- and low-depletion glacial
${\rm{\Delta }}R\left( \theta \right)$
when constructing the age-depth model for all 14C samples at depths from 0–412 cm. Deeper in the core, we apply the appropriate high- and low-depletion glacial
![]() ${\rm{\Delta }}R\left( \theta \right)$
.
${\rm{\Delta }}R\left( \theta \right)$
.
When fitting our OxCal p-sequence, we have selected a variable k, P_Sequence(“”,100,5,U(-2,2)), with core depths provided in m. There is one clear outlier with the sample at depth 5.52m (14,025 ± 50 14C yrs BP) being significantly older than the next five samples upcore at 5.92, 6.72, 7.57, 8.37, and 8.52m (ca. 13,300–13,900 14C yrs BP). We have therefore used an outlier model with a prior probability of 0.05 of a sample being an outlier: Outlier_Model(“General”,T(5),U(0,4),"t”).
The resultant models (with their uncertainty bands) are shown in Figure 9. The green age-depth model represents the chronology had core MD02-2496 been in a high-depletion
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{GS}$
polar scenario throughout the glacial period before shifting to
${\rm{\Delta }}R_{MD02 - 2496}^{GS}$
polar scenario throughout the glacial period before shifting to
![]() ${\rm{\Delta }}R_{MD02 - 2496}^{Hol}$
in the Holocene. In the blue age-depth model,
${\rm{\Delta }}R_{MD02 - 2496}^{Hol}$
in the Holocene. In the blue age-depth model,
![]() ${\rm{\Delta }}R\left( \theta \right) = \;{\rm{\Delta }}R_{MD02 - 2496}^{Hol}$
throughout. This represents the chronology if the climate at site MD02-2496 had followed a low-depletion polar scenario throughout the glacial where no additional regional changes in oceanic 14C depletion were seen beyond those large-scale effects captured in Marine20.
${\rm{\Delta }}R\left( \theta \right) = \;{\rm{\Delta }}R_{MD02 - 2496}^{Hol}$
throughout. This represents the chronology if the climate at site MD02-2496 had followed a low-depletion polar scenario throughout the glacial where no additional regional changes in oceanic 14C depletion were seen beyond those large-scale effects captured in Marine20.

Figure 9 Age-depth models of deep-sea core MD02-2496 (49ºN 127ºW) under a low (blue) and high (green) depletion polar scenario using an OxCal p-sequence (with a variable k and general outlier model). Changes in depletion can be achieved by modification of DeltaR within OxCal’s p-sequence model. Core depths are given in m. We consider the age of a hypothetical event at 15.2 m within the core. Again, the OxCal calendar age scale runs from left (oldest) to right (youngest/more recent).
If we are interested in the calendar age of a hypothetical event at depth of 15.2m in the core (as illustrated in Figure 9), then we can obtain calendar age estimates from the separate age-depth models under the low- and high-depletion glacial polar scenarios. These calendar ages are shown in Table 2. Again, these can be combined by selecting the most extreme calendar ages to create a wide age-bracketing that hopefully includes the true calendar age.
Table 2 Calendar age estimates of the MD02-2496 (49ºN) sediment core at a depth of 15.2 m based on OxCal’s p-sequence age-depth modeling (with a variable k and general outlier model) under the low- and high-depletion polar scenarios.

We note that it is possible that the true
![]() ${\rm{\Delta }}R\left( \theta \right)$
flips between the high- and low-depletion polar glacial scenarios over time throughout the core as we move from stadials to interstadials. Our suggested bracketing age-depth models assume a constant
${\rm{\Delta }}R\left( \theta \right)$
flips between the high- and low-depletion polar glacial scenarios over time throughout the core as we move from stadials to interstadials. Our suggested bracketing age-depth models assume a constant
![]() ${\rm{\Delta }}R\left( \theta \right)$
depletion scenario (either high or low). Such scenario flips could change the age-depth model substantially. However, preliminary testing suggests that even with changes from high- to low-depletion within the core, the calendar ages from the fixed, bounding, glacial scenarios bracket the calendar ages of the scenario-changing model at any given depth. Users of age-depth models may also wish to place a uniform prior on their estimate of
${\rm{\Delta }}R\left( \theta \right)$
depletion scenario (either high or low). Such scenario flips could change the age-depth model substantially. However, preliminary testing suggests that even with changes from high- to low-depletion within the core, the calendar ages from the fixed, bounding, glacial scenarios bracket the calendar ages of the scenario-changing model at any given depth. Users of age-depth models may also wish to place a uniform prior on their estimate of
![]() ${\rm{\Delta }}R\left( \theta \right)$
with upper- and lower-bounds taken from the low- and high-depletion scenarios. Such a model would provide a single age-depth model. However, if the climate flips rapidly between climate scenarios, with the appropriate
${\rm{\Delta }}R\left( \theta \right)$
with upper- and lower-bounds taken from the low- and high-depletion scenarios. Such a model would provide a single age-depth model. However, if the climate flips rapidly between climate scenarios, with the appropriate
![]() ${\rm{\Delta }}R\left( \theta \right)$
also flipping between its upper and lower limits, this approach may give over-confident estimates.
${\rm{\Delta }}R\left( \theta \right)$
also flipping between its upper and lower limits, this approach may give over-confident estimates.
4.3 Incorporating Paleoclimatic and Proxy Evidence on the Sea-Ice Extent into Calibration
We recommend that all those calibrating glacial period 14C samples from polar regions present the results from both bracketing scenarios, with the belief that the true calendar ages should lie between the values obtained under the two limiting scenarios. However, we recognize that some users may have expert knowledge from independent palaeoclimatic/proxy evidence as to which scenario is more appropriate. Such users might therefore, quite reasonably, wish to argue one option is more plausible than the other; or indeed they may believe that an intermediate 14C depletion scenario (which would result in intermediate calendar ages) is most suitable. We leave such interpretation up to the individual expert and would encourage them to do so if it is felt appropriate, provided their reasoning is fully documented.
Further into the future, it may be possible to determine more precise
![]() ${\rm{\Delta }}R\left( \theta \right)$
regional adjustments in polar regions using paleoclimatic and proxy evidence to infer the extent of sea-ice. Such proxy information might allow one to scale, for any individual 14C sample, the
${\rm{\Delta }}R\left( \theta \right)$
regional adjustments in polar regions using paleoclimatic and proxy evidence to infer the extent of sea-ice. Such proxy information might allow one to scale, for any individual 14C sample, the
![]() ${\rm{\Delta }}R\left( \theta \right)$
between the present-day
${\rm{\Delta }}R\left( \theta \right)$
between the present-day
![]() ${\rm{\Delta }}{R_{20}}$
value and that representing the GS/CS values of the LSG OGCM. If such a procedure was shown to improve our estimation of polar
${\rm{\Delta }}{R_{20}}$
value and that representing the GS/CS values of the LSG OGCM. If such a procedure was shown to improve our estimation of polar
![]() ${\rm{\Delta }}R\left( \theta \right)$
, then it would also provide more precise calendar dating when calibrating polar 14C samples. Reconstructing sea-ice variation is possible but challenging. Several proxies have been proposed. These include micropaleontological transfer functions based on diatoms (e.g., Gersonde et al. Reference Gersonde, Crosta, Abelmann and Armand2005) and dinocysts (de Vernal et al. Reference de Vernal, Henry, Matthiessen, Mudie, Rochon, Boessenkool, Eynaud, Grøsfjeld, Guiot and Hamel2001); molecular abundance of a particular hydrocarbon (IP25) synthesized by diatoms living at the bottom of sea-ice (Belt and Müller Reference Belt and Müller2013); and stomach-oil deposits from snow petrels (McClymont et al. Reference McClymont, Bentley, Hodgson, Spencer-Jones, Wardley, West, Croudace, Berg, Gröcke, Kuhn, Jamieson, Sime and Phillips2022; Thatje et al. Reference Thatje, Hillenbrand, Mackensen and Larter2008). Several authors have used these proxies to show systematic changes of sea-ice that are linked to abrupt climate changes (Hoff et al. Reference Hoff, Rasmussen, Stein, Ezat and Fahl2016; Méheust et al. Reference Méheust, Stein, Fahl and Gersonde2018; Stein et al. Reference Stein, Fahl, Gierz, Niessen and Lohmann2017). To investigate whether such a sliding, sea-ice proxy-informed,
${\rm{\Delta }}R\left( \theta \right)$
, then it would also provide more precise calendar dating when calibrating polar 14C samples. Reconstructing sea-ice variation is possible but challenging. Several proxies have been proposed. These include micropaleontological transfer functions based on diatoms (e.g., Gersonde et al. Reference Gersonde, Crosta, Abelmann and Armand2005) and dinocysts (de Vernal et al. Reference de Vernal, Henry, Matthiessen, Mudie, Rochon, Boessenkool, Eynaud, Grøsfjeld, Guiot and Hamel2001); molecular abundance of a particular hydrocarbon (IP25) synthesized by diatoms living at the bottom of sea-ice (Belt and Müller Reference Belt and Müller2013); and stomach-oil deposits from snow petrels (McClymont et al. Reference McClymont, Bentley, Hodgson, Spencer-Jones, Wardley, West, Croudace, Berg, Gröcke, Kuhn, Jamieson, Sime and Phillips2022; Thatje et al. Reference Thatje, Hillenbrand, Mackensen and Larter2008). Several authors have used these proxies to show systematic changes of sea-ice that are linked to abrupt climate changes (Hoff et al. Reference Hoff, Rasmussen, Stein, Ezat and Fahl2016; Méheust et al. Reference Méheust, Stein, Fahl and Gersonde2018; Stein et al. Reference Stein, Fahl, Gierz, Niessen and Lohmann2017). To investigate whether such a sliding, sea-ice proxy-informed,
![]() ${\rm{\Delta }}R(\theta $
) correction improves calendar dating would require suitable independent testing: either by comparing the resultant core chronology against absolute chronologies; or with downcore evidence of local MRA changes (e.g., using tephra). Such work goes beyond that possible here but would be a valuable further avenue of study.
${\rm{\Delta }}R(\theta $
) correction improves calendar dating would require suitable independent testing: either by comparing the resultant core chronology against absolute chronologies; or with downcore evidence of local MRA changes (e.g., using tephra). Such work goes beyond that possible here but would be a valuable further avenue of study.
5 CONCLUSIONS
Estimating the evolution of surface-ocean 14C levels in polar regions from 55,000–0 cal yr BP, and consequently calibrating marine 14C samples from these high-latitude region, is highly challenging. All of the MarineXX radiocarbon age calibration curves (Marine20 and all earlier products) only aim to represent global-scale changes in oceanic 14C levels (Heaton et al. Reference Heaton, Köhler, Butzin, Bard, Reimer, Austin, Bronk Ramsey, Grootes, Hughen and Kromer2020, Reference Heaton, Bard, Bronk Ramsey, Butzin, Hatte, Hughen, Köhler and Reimer2022). The recent Marine20 curve incorporates large-scale changes in paleoclimate and the carbon cycle which occurred during the glacial: most notably in CO2 (Köhler et al. Reference Köhler, Nehrbass-Ahles, Schmitt, Stocker and Fischer2017), atmospheric 14C (Reimer et al. Reference Reimer, Austin, Bard, Bayliss, Blackwell, Ramsey, Butzin, Cheng, Edwards and Friedrich2020), wind speed (Kageyama et al. Reference Kageyama, Harrison, Kapsch, Lofverstrom, Lora, Mikolajewicz, Sherriff-Tadano, Vadsaria, Abe-Ouchi and Bouttes2021; Kohfeld et al. Reference Kohfeld, Graham, de Boer, Sime, Wolff, Le Quéré and Bopp2013; Petit et al. Reference Petit, Mourner, Jouzel, Korotkevich, Kotlyakov and Lorius1990) and AMOC (Böhm et al. Reference Böhm, Lippold, Gutjahr, Frank, Blaser, Antz, Fohlmeister, Frank, Andersen and Deininger2015; Henry et al. Reference Henry, McManus, Curry, Roberts, Piotrowski and Keigwin2016; Oka et al. Reference Oka, Abe-Ouchi, Sherriff-Tadano, Yokoyama, Kawamura and Hasumi2021). However, in polar regions, we expect that during glacial periods there may have been substantial further, more localized, changes in the level of oceanic 14C depletion. This additional polar variation is due, in particular, to increases in the volume and density of sea-ice at high-latitudes during these periods (Butzin et al. Reference Butzin, Prange and Lohmann2005, Reference Butzin, Köhler and Lohmann2017, Reference Butzin, Heaton, Köhler and Lohmann2020). These temporal variations in the MRA at high-latitudes during the glacial period are not represented in the global-scale MarineXX curves, and so must be modeled through
![]() ${\rm{\Delta }}R\left( \theta \right)$
.
${\rm{\Delta }}R\left( \theta \right)$
.
When calibrating marine 14C samples against Marine20, or any MarineXX curve, using an appropriate value of
![]() ${\rm{\Delta }}R\left( \theta \right)$
is critical. Typically, we are only able to estimate a modern-day value for
${\rm{\Delta }}R\left( \theta \right)$
is critical. Typically, we are only able to estimate a modern-day value for
![]() ${\rm{\Delta }}R\left( \theta \right)$
using 14C samples from the recent past. This (modern-day) estimate of
${\rm{\Delta }}R\left( \theta \right)$
using 14C samples from the recent past. This (modern-day) estimate of
![]() ${\rm{\Delta }}{R_\;}$
is unlikely to be suitable for application when calibrating high-latitude (outside ca. 40ºS–40ºN) marine 14C samples from the glacial period against Marine20, or any MarineXX curve. We expect that, for polar oceans, due to the presence of regional sea-ice, the value of
${\rm{\Delta }}{R_\;}$
is unlikely to be suitable for application when calibrating high-latitude (outside ca. 40ºS–40ºN) marine 14C samples from the glacial period against Marine20, or any MarineXX curve. We expect that, for polar oceans, due to the presence of regional sea-ice, the value of
![]() ${\rm{\Delta }}R\left( \theta \right)$
may have been substantially greater during the glacial period than those values seen during the non-glacial recent past. Under some modeled climate scenarios, the increase in the value of
${\rm{\Delta }}R\left( \theta \right)$
may have been substantially greater during the glacial period than those values seen during the non-glacial recent past. Under some modeled climate scenarios, the increase in the value of
![]() ${\rm{\Delta }}R\left( \theta \right)$
in polar regions could extend up to ca. 1500 14C yrs (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020).
${\rm{\Delta }}R\left( \theta \right)$
in polar regions could extend up to ca. 1500 14C yrs (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020).
If we calibrate a polar marine 14C sample from the glacial period using a modern-day estimate of
![]() ${\rm{\Delta }}R\left( \theta \right)$
, without recognizing the potential for this
${\rm{\Delta }}R\left( \theta \right)$
, without recognizing the potential for this
![]() ${\rm{\Delta }}R\left( \theta \right)$
to increase in glacial conditions, we are likely to obtain a calibrated age that is biased (older than the true calendar age) and over precise. Current proxy records are not sufficiently reliable to reconstruct the climatic conditions at high-latitudes (including the extent of sea-ice, ocean ventilation and wind strengths) during the glacials. Due to this considerable uncertainty in polar paleoclimate, it is not possible to accurately or precisely model
${\rm{\Delta }}R\left( \theta \right)$
to increase in glacial conditions, we are likely to obtain a calibrated age that is biased (older than the true calendar age) and over precise. Current proxy records are not sufficiently reliable to reconstruct the climatic conditions at high-latitudes (including the extent of sea-ice, ocean ventilation and wind strengths) during the glacials. Due to this considerable uncertainty in polar paleoclimate, it is not possible to accurately or precisely model
![]() ${\rm{\Delta }}R\left( \theta \right)$
and generate polar radiocarbon age calibration curves. The LSG OGCM model does permit modeling of surface open-ocean 14C levels in polar regions under fixed climate scenarios (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020). However, direct use of these LSG OGCM estimates for calibration is not trivial.
${\rm{\Delta }}R\left( \theta \right)$
and generate polar radiocarbon age calibration curves. The LSG OGCM model does permit modeling of surface open-ocean 14C levels in polar regions under fixed climate scenarios (Butzin et al. Reference Butzin, Heaton, Köhler and Lohmann2020). However, direct use of these LSG OGCM estimates for calibration is not trivial.
We propose that those wishing to calibrate high-latitude (outside ca. 40ºS–40ºN) marine 14C samples may continue to use the Marine20 curves but with a simple and approximate adjustment to the value of
![]() ${\rm{\Delta }}R\left( \theta \right)$
dependent upon the calendar age and latitude of the sample. We suggest that those calibrating polar marine 14C samples from the Holocene proceed as they traditionally have done, by estimating a regional
${\rm{\Delta }}R\left( \theta \right)$
dependent upon the calendar age and latitude of the sample. We suggest that those calibrating polar marine 14C samples from the Holocene proceed as they traditionally have done, by estimating a regional
![]() ${\rm{\Delta }}{R_{20}}$
based on samples from the recent past, and then assuming this
${\rm{\Delta }}{R_{20}}$
based on samples from the recent past, and then assuming this
![]() ${\rm{\Delta }}{R_{20}}\;$
value remains applicable for their undated sample.
${\rm{\Delta }}{R_{20}}\;$
value remains applicable for their undated sample.
For those wishing to estimate the calendar ages of polar marine 14C samples from glacial periods we suggest using two bracketing surface-ocean 14C depletion scenarios. The first (low-depletion) scenario assumes that there have been no regional changes in polar
![]() ${\rm{\Delta }}R\left( \theta \right)$
over time. The calendar age of the 14C sample under this scenario can be obtained by calibrating against Marine20 using an estimate of
${\rm{\Delta }}R\left( \theta \right)$
over time. The calendar age of the 14C sample under this scenario can be obtained by calibrating against Marine20 using an estimate of
![]() ${\rm{\Delta }}R_{20}^{Hol}$
based on samples from the recent past in the location of interest. The second (high-depletion) scenario aims to represent the GS glacial scenario of the LSG OGCM (which includes considerable high-latitude sea-ice). This scenario can be approximated with Marine20 simply by increasing the (recent-past) estimate of
${\rm{\Delta }}R_{20}^{Hol}$
based on samples from the recent past in the location of interest. The second (high-depletion) scenario aims to represent the GS glacial scenario of the LSG OGCM (which includes considerable high-latitude sea-ice). This scenario can be approximated with Marine20 simply by increasing the (recent-past) estimate of
![]() ${\rm{\Delta }}R_{20}^{Hol}$
by a latitude dependent constant
${\rm{\Delta }}R_{20}^{Hol}$
by a latitude dependent constant
![]() ${\rm{\Delta }}R_\;^{Hol\; \to \;GS}$
. This boost to the localized 14C depletion aims to provide an upper limit on the potential level of additional regional polar 14C depletion in the glacial.
${\rm{\Delta }}R_\;^{Hol\; \to \;GS}$
. This boost to the localized 14C depletion aims to provide an upper limit on the potential level of additional regional polar 14C depletion in the glacial.
We hope that the calibrated age estimates obtained using Marine20 under these two polar glacial depletion scenarios will bracket the true calendar age of the 14C sample. The low-depletion scenario will provide an upper calendar age limit, the high-depletion a lower calendar age limit. If no external information is available regarding which depletion scenario is more appropriate, then one may only be able to infer that the true calendar age lies between these upper and lower limits. This range will typically be wide. However, if paleoclimatic proxies are available, for example on the extent of sea-ice, then a user may be able to infer which scenario is more appropriate. While we recommend that the calibrated dates under both high- and low-depletion scenarios are always shown so that a reader can understand the likely maximum range of calibrated dates, a user with independent information on the most suitable depletion scenario may focus their later interpretation on that provided their reasoning is documented.
As knowledge increases, we expect that polar-specific calibration curves will become available. Such advances could be obtained via improved modeling, although this will require significantly improved understanding of paleoceanographic proxy information to better reconstruct past polar climate. Alternatively, polar marine curves could be generated by collecting 14C samples in the relevant ocean locations, if it is possible to date these samples via alternative techniques.
ACKNOWLEDGMENTS
TJH is supported by the BA/Leverhulme (SRG22/220289), NERC (NE/X009815/1), and a Leverhulme Trust Fellowship RF-2019-140/9. E. Bard and M. Butzin are funded by the joint ANR-DFG project MARCARA. P. Köhler and also M. Butzin were supported by the German Federal Ministry of Education and Research (BMBF), as Research for Sustainability initiative (FONA); www.fona.de through the PalMod project (grant numbers: 01LP1505B, 01LP1919A).
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit https://doi.org/10.1017/RDC.2023.42
Appendix A
Table A1 Key notation used to define various components of marine reservoir age.

Table A2 Estimates of the latitudinal increases Δ
![]() $R_\;^{Hol\; \to \;GS}$
(and Δ
$R_\;^{Hol\; \to \;GS}$
(and Δ
![]() $R_\;^{Hol\; \to \;CS}$
) to be applied to modern-day Δ
$R_\;^{Hol\; \to \;CS}$
) to be applied to modern-day Δ
![]() ${R_{20}}$
if we wish to recreate the GS (and CS) scenarios of the LSG OGCM in the glacial periods while still using the Marine20 curve. Those values highlighted in gold (outside ∼ 40ºS–40ºN) have shifts which fall outside the mean ±2
${R_{20}}$
if we wish to recreate the GS (and CS) scenarios of the LSG OGCM in the glacial periods while still using the Marine20 curve. Those values highlighted in gold (outside ∼ 40ºS–40ºN) have shifts which fall outside the mean ±2
![]() $\sigma $
uncertainty on the value of
$\sigma $
uncertainty on the value of
![]() $R_{20}^{GlobalAv}\left( \theta \right)$
that is already incorporated into the global-scale Marine20 curve. We suggest that, when calibrating glacial-period 14C samples from marine locations at these higher (gold) latitudes, users should employ our bracketing approach to allow for low- and high-depletion glacial polar scenarios. At lower latitudes (highlighted in green) we cautiously suggest that users do not need to consider such bracketing as the increase to recreate the GS (or CS) scenarios falls within the existing uncertainty on the Marine20 curve. Users with sites at latitudes not specified above should interpolate (although remain aware that all these estimates are, by design, coarse and hence do not need to focus on over-precision).
$R_{20}^{GlobalAv}\left( \theta \right)$
that is already incorporated into the global-scale Marine20 curve. We suggest that, when calibrating glacial-period 14C samples from marine locations at these higher (gold) latitudes, users should employ our bracketing approach to allow for low- and high-depletion glacial polar scenarios. At lower latitudes (highlighted in green) we cautiously suggest that users do not need to consider such bracketing as the increase to recreate the GS (or CS) scenarios falls within the existing uncertainty on the Marine20 curve. Users with sites at latitudes not specified above should interpolate (although remain aware that all these estimates are, by design, coarse and hence do not need to focus on over-precision).