Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T13:40:13.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Semidefinite Programming BasedAlgorithms for the Sparsest Cut Problem

Published online by Cambridge University Press:  17 June 2011

Luis A.A. Meira  and
Flávio K. Miyazawa
Luis A.A. Meira
Affiliation:
Federal University of Sao Paulo, Rua botucatu 740 Edif Octavio de Carvalho, 04023-900 Sao Paulo, Brazil. augusto.meira@unifesp.br
Flávio K. Miyazawa
Affiliation:
University of Campinas, Brazil. fkm@ic.unicamp.br
Get access

Abstract

In this paper we analyze a known relaxation for the Sparsest Cut problem based on positive semidefinite constraints, and we present a branch and bound algorithm and heuristics based on this relaxation. The relaxed formulation and the algorithms were tested on small and moderate sized instances. It leads to values very close to the optimum solution values. The exact algorithm could obtain solutions for small and moderate sized instances, and the best heuristics obtained optimum or near optimum solutions for all testedinstances. The semidefinite relaxation gives a lower bound $\frac{C}{W}$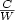 and each heuristic produces a cut S with a ratio $\frac{c_S}{w_S}$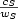, where either cS is at most a factor of C or wS is at least a factor of W. We solved the semidefinite relaxation using a semi-infinite cut generation with a commercial linear programming package adapted to the sparsest cut problem. We showed that the proposed strategy leads to a better performance compared to the use of a known semidefinite programming solver.

Keywords

Semidefinite programmingSparsest Cutcombinatorics
Type
Research Article
Information
RAIRO - Operations Research , Volume 45 , Issue 2 , April 2011 , pp. 75 - 100
Copyright
© EDP Sciences, ROADEF, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S. Arora, J.R. Lee and A. Naor, Euclidean distortion and the sparsest cut, in STOC '05: Proceedings of the thirty-seventh annual ACM symposium on Theory of computing. ACM New York, NY, USA (2005) 553–562.
S. Arora, S. Rao and U. Vazirani, Expander flows, geometric embeddings and graph partitioning, in STOC '04: Proceedings of the thirty-sixth annual ACM symposium on Theory of computing. ACM, New York, NY, USA (2004) 222–231.
Bracht, E.C., Meira, L.A.A. and Miyazawa, F.K., A greedy approximation algorithm for the uniform metric labeling problem analyzed by a primal-dual technique. ACM Journal of Experimental Algorithmics 10 (2005) 2.11.
S. Chawla, A. Gupta and H. Räcke, Embeddings of negative-type metrics and an improved approximation to generalized sparsest cut, in SODA '05: Proceedings of the sixteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA (2005) 102–111.
S. Chawla, R. Krauthgamer, R. Kumar, Y. Rabani and D. Sivakumar, On the hardness of approximating multicut and sparsest-cut, in 20th Annual IEEE Conference on Computational Complexity (2005) 144–153.
N.R. Devanur, S.A. Khot, R. Saket and N.K. Vishnoi, Integrality gaps for sparsest cut and minimum linear arrangement problems, in STOC '06: Proceedings of the thirty-eighth annual ACM symposium on Theory of computing. ACM Press, New York, NY, USA (2006) 537–546.
B.M.P. Fraticelli, Semidefinite Cuts and Partial Convexification Techniques with Applications to Continuous Nonconvex Optimization, Stochastic Integer Programming, and Facility Layout Problems. Ph.D. thesis, Virginia Polytechnic Institute (2001).
Goemans, M.X. and Williamson, D.P., Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. Journal of the Association for Computing Machinery 42 (1995) 1115–1145. CrossRef
C. Helmberg, Semidefinite programming for combinatorial optimization. Habilitationsschrift. ZIB-Report ZR-00-34, Konrad-Zuse-Zentrum (2000).
T. Hofmeister and M. Hühne, Semidefinite programming and its applications to approximation algorithms, in Lectures on Proof Verification and Approximation Algorithms (the book grow out of a Dagstuhl Seminar, 1997), Springer-Verlag, London, UK (1998) 263–298.
K. Krishnan and J.E. Mitchell, Semi-infinite linear programming approaches to semidefinite programming (SDP) problems, in Novel approaches to hard discrete optimization problems, Fields Institute Communications Series 37. edited by P.M. Pardalos and H. Wolkowicz, AMS (2003) 123–142.
Krishnan, K. and Mitchell, J.E., A unifying framework for several cutting plane methods for semidefinite programming. Optim. Methods Softw. 21 (2006) 57–74. CrossRef
Krishnan, K. and Mitchell, J.E., A semidefinite programming based polyhedral cut-and-price approach for the maxcut problem. Comput. Opt. Appl. 33 (2006) 51–71. CrossRef
M. Laurent and R. Rendl, Semidefinite programming and integer programming, in Handbook on Discrete Optimization, edited by K. Aardal, G. Nemhauser and R. Weismantel. Elsevier B.V. (2005) 393–514.
T. Leighton and S. Rao, An approximate max-flow min-cut theorem for uniform multicommodity flow problems with applications to approximation algorithms, Proc. 29th Ann. IEEE Symp. on Foundations of Comput. Sci., IEEE Computer Society (1988) 422–431.
Mitchell, J.E., Restarting after branching in the SDP approach to MAX-CUT and similar combinatorial optimization problems. J. Comb. Optim. 5 (2001) 151–166. CrossRef
Sherali, H.D. and Fraticelli, B.M.P., Enhancing rlt relaxations via a new class of semidefinite cuts. J. Glob. Optim. 22 (2002) 233–261. CrossRef
D.B. Shmoys, Cut problems and their application to divide-and-conquer, in Approximation Algorithms for NP-Hard Problems, edited by D. Hochbaum. PWS Publishing (1996) 192–235.
Wang, S. and Siskind, J., Image segmentation with ratio cut. IEEE Trans. Pattern Anal. Mach. Intell. 25 (2003) 675–690. CrossRef
M. Yamashita, SDPA – Semidefinite programming solver (2002), available at: http://grid.r.dendai.ac.jp/sdpa/.
Yang, H., Ye, Y. and Zhang, J., An approximation algorithm for scheduling two parallel machines with capacity constraints. Discrete Appl. Math. 130 (2003) 449–467. CrossRef