Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-11T13:33:44.128Z Has data issue: false hasContentIssue false
  • English
  • Français

Undecidability of Topologicaland Arithmetical Propertiesof Infinitary Rational Relations

Published online by Cambridge University Press:  15 November 2003

Olivier Finkel
Olivier Finkel*
Affiliation:
Équipe de Logique Mathématique, U.F.R. de Mathématiques, Université Paris-7, 2 place Jussieu, 75251 Paris Cedex 05, France; finkel@logique.jussieu.fr.
Get access

Abstract

We prove that for every countable ordinal α one cannot decidewhether a given infinitary rational relation is in the Borel class ${\bf \Sigma_{\alpha}^0}$ 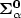(respectively ${\bf \Pi_{\alpha}^0}$ 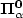). Furthermoreone cannotdecide whether a given infinitary rational relation is a Borel set or a ${\bf \Sigma_{1}^1}$ 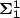-complete set. We prove some recursive analogues to theseproperties. In particular one cannot decide whether an infinitary rational relation is anarithmetical set.We then deduce from the proof ofthese results some other ones, like: one cannot decide whether thecomplement ofan infinitary rational relation is also an infinitary rational relation.

Keywords

Infinitary rational relationstopological propertiesBorel andanalytic setsarithmetical propertiesdecision problems.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 37 , Issue 2 , April 2003 , pp. 115 - 126
Copyright
© EDP Sciences, 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

M.-P. Béal, O. Carton, C. Prieur and J. Sakarovitch, Squaring Transducers: An Efficient Procedure for Deciding Functionality and Sequentiality of Transducers, in Proc. of LATIN 2000, edited by G. Gonnet, D. Panario and A. Viola. Springer, Lect. Notes Comput. Sci. 1776 (2000) 397-406.
J. Berstel, Transductions and Context Free Languages. Teubner Verlag (1979).
J.R. Büchi, On a Decision Method in Restricted Second Order Arithmetic, Logic Methodology and Philosophy of Science, in Proc. 1960 Int. Congr. Stanford University Press (1962) 1-11.
Choffrut, C., Une Caractérisation des Fonctions Séquentielles et des Fonctions Sous-Séquentielles en tant que Relations Rationnelles. Theoret. Comput. Sci. 5 (1977) 325-338. CrossRef
C. Choffrut and S. Grigorieff, Uniformization of Rational Relations, Jewels are Forever, edited by J. Karhumäki, H. Maurer, G. Paun and G. Rozenberg. Springer (1999) 59-71.
Finkel, O., On the Topological Complexity of Infinitary Rational Relations. Theoret. Informatics Appl. 37 (2003) 105-113. CrossRef
O. Finkel, On Infinitary Rational Relations and Borel Sets, in Proc. of the Fourth International Conference on Discrete Mathematics and Theoretical Computer Science DMTCS'03, 7-12 July 2003, Dijon, France. Springer, Lect. Notes Comput. Sci. (to appear).
Frougny, C. and Sakarovitch, J., Synchronized Relations of Finite and Infinite Words. Theoret. Comput. Sci. 108 (1993) 45-82. CrossRef
F. Gire, Relations Rationnelles Infinitaires, Thèse de troisième cycle. Université Paris-7, France (1981).
F. Gire, Une Extension aux Mots Infinis de la Notion de Transduction Rationnelle, in 6th GI Conf. Springer, Lect. Notes Comput. Sci. 145 (1983) 123-139.
F. Gire and M. Nivat, Relations Rationnelles Infinitaires. Calcolo XXI (1984) 91-125.
F. Gire, Contribution à l'Étude des Langages et Relations Infinitaires, Thèse d'État. Université Paris-7, France (1986).
A.S. Kechris, Classical Descriptive Set Theory. Springer-Verlag (1995).
Landweber, L.H., Decision Problems for ω-Automata. Math. Syst. Theory 3 (1969) 376-384. CrossRef
H. Lescow and W. Thomas, Logical Specifications of Infinite Computations, in A Decade of Concurrency, edited by J.W. de Bakker et al. Springer, Lect. Notes Comput. Sci. 803 (1994) 583-621.
Y.N. Moschovakis, Descriptive Set Theory. North-Holland, Amsterdam (1980).
D. Perrin and J.-E. Pin, Infinite Words. Book in preparation, available from http://www.liafa.jussieu.fr/jep/InfiniteWords.html
Pin, J.-E., Logic, Semigroups and Automata on Words. Ann. Math. Artificial Intelligence 16 (1996) 343-384. CrossRef
C. Prieur, Fonctions Rationnelles de Mots Infinis et Continuité, Thèse de Doctorat. Université Paris-7, France (2000).
Prieur, C., How to Decide Continuity of Rational Functions on Infinite Words. Theoret. Comput. Sci. 250 (2001) 71-82. CrossRef
P. Simonnet, Automates et Théorie Descriptive, Ph.D. Thesis. Université Paris-7, France (1992).
Staiger, L., Hierarchies of Recursive ω-Languages. J. Inform. Process. Cybernetics EIK 22 (1986) 219-241.
L. Staiger, ω-Languages, Handbook Formal Languages, Vol. 3, edited by G. Rozenberg and A. Salomaa. Springer-Verlag, Berlin (1997).
W. Thomas, Automata on Infinite Objects, edited by J. Van Leeuwen. Elsevier, Amsterdam, Handb. Theoret. Comput. Sci. B (1990) 133-191.