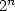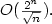Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jirásková, Galina
and
Pighizzini, Giovanni
2009.
Language and Automata Theory and Applications.
Vol. 5457,
Issue. ,
p.
458.
Jirásková, Galina
and
Pighizzini, Giovanni
2011.
Optimal simulation of self-verifying automata by deterministic automata.
Information and Computation,
Vol. 209,
Issue. 3,
p.
528.
YAN, Yong-yi
CHEN, Zeng-qiang
and
LIU, Zhong-xin
2014.
Verification analysis of self-verifying automata via semi-tensor product of matrices.
The Journal of China Universities of Posts and Telecommunications,
Vol. 21,
Issue. 4,
p.
96.
Jirásek, Jozef Štefan
Jirásková, Galina
and
Szabari, Alexander
2015.
Computer Science -- Theory and Applications.
Vol. 9139,
Issue. ,
p.
231.
Marais, Laurette
and
van Zijl, Lynette
2016.
Descriptional Complexity of Formal Systems.
Vol. 9777,
Issue. ,
p.
180.
Jirásková, Galina
2016.
Descriptional Complexity of Formal Systems.
Vol. 9777,
Issue. ,
p.
29.
Marais, Laurette
and
van Zijl, Lynette
2017.
Descriptional Complexity of Non-Unary Self-Verifying Symmetric Difference Automata.
Electronic Proceedings in Theoretical Computer Science,
Vol. 252,
Issue. ,
p.
157.
Marais, Laurette
and
van Zijl, Lynette
2022.
Descriptional Complexity of Non-Unary Self-Verifying Symmetric Difference Automata.
International Journal of Foundations of Computer Science,
Vol. 33,
Issue. 03n04,
p.
313.