Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T14:47:06.347Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing the jth solution of a first-order query

Published online by Cambridge University Press:  18 January 2008

Guillaume Bagan ,
Arnaud Durand ,
Etienne Grandjean  and
Frédéric Olive
Guillaume Bagan
Affiliation:
GREYC, Université de Caen, ENSICAEN, CNRS, Campus 2, 14032 Caen Cedex, France; gbagan@info.unicaen.fr; grandjean@info.unicaen.fr
Arnaud Durand
Affiliation:
Équipe de Logique Mathématique, Université Denis Diderot, CNRS UMR 7056, 2 place Jussieu, 75251 Paris Cedex 05, France; durand@logique.jussieu.fr
Etienne Grandjean
Affiliation:
GREYC, Université de Caen, ENSICAEN, CNRS, Campus 2, 14032 Caen Cedex, France; gbagan@info.unicaen.fr; grandjean@info.unicaen.fr
Frédéric Olive
Affiliation:
LIF, Université Aix-Marseille 1, CNRS, 39 rue Joliot Curie, 13453 Marseille Cedex 13, France; frederic.olive@lif.univ-mrs.fr
Get access

Abstract

We design algorithms of “optimal" data complexity for several natural problems about first-order queries on structures of bounded degree. For that purpose, we first introduce a framework to deal with logical or combinatorial problems R ⊂ I x O whose instances x ∈ I may admit of several solutions R(x) = {y ∈ O : (x,y) ∈ R}. One associates to such a problem several specific tasks: compute a random (for the uniform probability distribution) solution y ∈ R(x); enumerate without repetition each solution yj in some specific linear order y0 < y1 < ... < yn-1 where R(x) = {y0,...,yn-1}; compute the solution yj of rankj in the linear order <. Algorithms of “minimal" data complexity are presented for the following problems: given any first-order formula $\varphi(\bar{v})$ 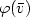and any structure S of bounded degree: (1) compute a random element of $\varphi(S)=\{\bar{a}: (S,\bar{a})\models\varphi(\bar{v})\}$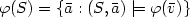; (2) compute the jth element of $\varphi(S)$ 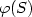for some linear order of $\varphi(S)$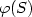; (3) enumerate the elements of $\varphi(S)$ 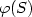in lexicographical order. More precisely, we prove that, for any fixed formula φ, the above problem (1) (resp. (2), (3)) can be computed within average constant time (resp. within constant time, with constant delay) after a linear (O(|S|)) precomputation. Our essential tool for deriving those complexity results is a normalization procedure of first-order formulas on bijective structures.

Keywords

Complexity of enumerationfirst-order queriesstructures of bounded degreelinear timeconstant timeconstant delay
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 1: A nonstandard spirit among computer scientists:a tribute to Serge Grigorieff at the occasion of his 60th birthday , January 2008 , pp. 147 - 164
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagan, G., Mso queries on tree decomposable structures are computable with linear delay, in Proc. 15th Annual Conference of the EACSL (CSL'06). Lect. Notes Comput. Sci. 4207 (2006) 167–181. CrossRef
G. Bagan, A. Durand and E. Grandjean, On acyclic conjunctive queries and constant delay enumeration, in Proc. 16th Annual Conference of the EACSL (CSL'07). Lect. Notes Comput. Sci. (2007) 208–222.
B. Courcelle, Linear delay enumeration and monadic second-order logic. Discrete Appl. Math. (2007) (to appear).
A. Durand and E. Grandjean, First-order queries on structures of bounded degree are computable with constant delay. ACM T. Comput. Logic (2007) 1–18.
Durand, A. and Olive, F., First-order queries over one unary function, in Proc. 15th Annual Conference of the EACSL (CSL'06). Lect. Notes Comput. Sci. 4207 (2006) 334–348. CrossRef
Flum, J., Frick, M. and Grohe, M., Query evaluation via tree decompositions. J. ACM 49 (2002) 716–752. CrossRef
Frick, M. and Grohe, M., Deciding first-order properties of locally tree decomposable structures. J. ACM 48 (2001) 1184–1206. CrossRef
Gottlob, G., Leone, N. and Scarcello, F., The complexity of acyclic conjunctive queries. J. ACM 48 (2001) 431–498. CrossRef
Grigorieff, S., Décidabilité et complexité des théories logiques. Collection Didactique INRIA 8 (1991) 7–97.
Grandjean, E. and Schwentick, T., Machine-independent characterizations and complete problems for deterministic linear time. SIAM J. Comput. 32 (2002) 196–230. CrossRef
L. Libkin, Elements of finite model theory. EATCS Series, Springer (2004).
S. Lindell, A normal form for first-order logic over doubly-linked data structures. Int. J. Found. Comput. Sci. (2006) (to appear).
R. Motwani and P. Raghavan, Randomized algorithms. Cambridge University Press (1995).
Papadimitriou, C. and Yannakakis, M., On the complexity of database queries. J. Comput. Syst. Sci. 58 (1999) 407–427. CrossRef
M.Y. Vardi, On the complexity of bounded-variable queries. Proc. Principles of Databases Systems (PODS'95), ACM Press (1995) 266–276.
Seese, D., Linear time computable problems and first-order descriptions. Math. Structures Comput. Sci. 6 (1996) 505–526.
M. Yannakakis, Algorithms for acyclic database schemes. Proc. Very Large Data Bases Conference (VLDB'81) (1981) 82–94.