Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T01:58:22.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Deciding whether a relation defined inPresburger logic can be defined in weaker logics

Published online by Cambridge University Press:  18 January 2008

Christian Choffrut
Christian Choffrut*
Affiliation:
LIAFA, Université de Paris 7, 2 place Jussieu, 75251 Paris Cedex 05; cc@liafa.jussieu.fr
Get access

Abstract

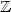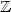We consider logics on $\mathbb{Z}$ and $\mathbb{N}$ which are weaker than Presburger arithmetic and we settle the following decision problem: given a k-ary relation on $\mathbb{Z}$ and $\mathbb{N}$ which are first order definable in Presburger arithmetic, are they definable in these weaker logics? These logics, intuitively, are obtained by considering modulo and threshold counting predicates for differences of two variables.

Keywords

Presburger arithmeticfirst order logicdecidability
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 1: A nonstandard spirit among computer scientists:a tribute to Serge Grigorieff at the occasion of his 60th birthday , January 2008 , pp. 121 - 135
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carton, O., Choffrut, C. and Grigorieff, S.. Decision problems for rational relations. RAIRO-Theor. Inf. Appl. 40 (2006) 255–275. CrossRef
C. Choffrut and M. Goldwurm. Timed automata with periodic clock constraints. J. Algebra Lang. Comput. 5 (2000) 371–404.
S. Eilenberg. Automata, Languages and Machines, volume A. Academic Press (1974).
S. Eilenberg and M.-P. Schützenbeger. Rational sets in commutative monoids. J. Algebra 13 (1969) 173–191.
S. Ginsburg and E.H. Spanier. Bounded regular sets. Proc. Amer. Math. Soc. 17 (1966) 1043–1049.
M. Koubarakis. Complexity results for first-order theories of temporal constraints. KR (1994) 379–390.
H. Läuchli and C. Savioz. Monadic second order definable relations on the binary tree. J. Symbolic Logic 52 (1987) 219–226.
A. Muchnik. Definable criterion for definability in presburger arithmentic and its application (1991). Preprint in russian.
P. Péladeau. Logically defined subsets of ${\mathbb{N}}^k$ . Theoret. Comput. Sci. 93 (1992) 169–193.
J.-E. Pin. Varieties of formal languages. Plenum Publishing Co., New-York (1986). (Traduction de Variétés de langages formels.)
J. Sakarovitch. Eléments de théorie des automates. Vuibert Informatique (2003).
A. Schrijver. Theory of Linear and Integer Programming. John Wiley & sons (1998).
C. Smoryński. Logical Number Theory I: An Introduction. Springer Verlag (1991).