Improved Lower Boundson the Approximabilityof the Traveling Salesman Problem

Abstract

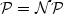This paper deals with lower bounds on the approximability of different subproblems of the TravelingSalesman Problem (TSP) which is known not to admit any polynomial time approximation algorithm in general(unless $\mathcal{P}=\mathcal{NP}$ ). First of all, we present an improved lower bound for the Traveling Salesman Problemwith Triangle Inequality, Delta-TSP for short. Moreover our technique, an extension of the method ofEngebretsen [11], also applies to the case of relaxed and sharpened triangle inequality,respectively, denoted $\Delta_\beta$ 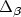-TSP for an appropriate β. In case of theDelta-TSP, we obtain a lowerbound of $\frac{3813}{3812}-\varepsilon$ 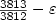on the polynomial-time approximability (for any small $\varepsilon> 0$ 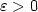), compared to the previous bound of $\frac{5381}{5380}-\varepsilon$ 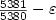in [11]. Incase of the $\Delta_\beta$ 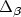-TSP, for the relaxed case ( $\beta> 1$ 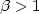) we present a lower bound of $\frac{3803+10\beta}{3804+8\beta}-\varepsilon$ , and for the sharpened triangle inequality( $\frac{1}{2}< \beta< 1$ 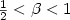), the lower bound is $\frac{7611+10\beta^2+5\beta}{7612+8\beta^2+4\beta}-\varepsilon$ 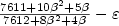. The latter result is of interestespecially since it shows that the TSP is $\mathcal{APX}$ 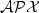-hard even if one comes arbitrarily close to the trivialcase that all edges have the same cost.