Article contents
On possible growths of arithmetical complexity
Published online by Cambridge University Press: 18 October 2006
Abstract
The arithmetical complexity of infinite words, defined by Avgustinovich, Fon-Der-Flaass and the author in 2000, is the number of words of length n which occur in the arithmetical subsequences of the infinite word. This is one of the modifications of the classical function of subword complexity, which is equal to the number of factors of the infinite word of length n. In this paper, we show that the orders of growth of the arithmetical complexity can behave as many sub-polynomial functions. More precisely, for each sequence u of subword complexity ƒu(n) and for each prime p ≥ 3 we build a Toeplitz word on the same alphabet whose arithmetical complexity is $a(n)=\Theta(n f_u(\lceil \log_p n \rceil))$ 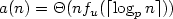 .
.
Information
- Type
- Research Article
- Information
- RAIRO - Theoretical Informatics and Applications , Volume 40 , Issue 3: Word Avoidability Complexity And Morphisms (WACAM) , July 2006 , pp. 443 - 458
- Copyright
- © EDP Sciences, 2006
References
- 9
- Cited by

