Article contents
On the power of randomization for job shop scheduling with k-units length tasks
Published online by Cambridge University Press: 05 June 2008
Abstract
In the job shop scheduling problem k-units-J m , there are m machines and each machine has an integer processing time of at most k time units. Each job consists of a permutation of m tasks corresponding to all machines and thus all jobs have an identicaldilation D. The contribution of this paper are the following results;(i) for $d=o(\sqrt{D})$ 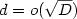 jobs and every fixed k, the makespan of an optimal schedule is at most D+ o(D), which extends the result of [3]for k=1; (ii) a randomized on-line approximation algorithm for k-units-J m ispresented. This is the on-line algorithm with the best known competitiveratio against an oblivious adversary for $d = o(\sqrt{D})$
jobs and every fixed k, the makespan of an optimal schedule is at most D+ o(D), which extends the result of [3]for k=1; (ii) a randomized on-line approximation algorithm for k-units-J m ispresented. This is the on-line algorithm with the best known competitiveratio against an oblivious adversary for $d = o(\sqrt{D})$ 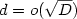 and k > 1; (iii) different processing times yield harder instances than identicalprocessing times. There is no 5/3 competitive deterministic on-linealgorithm for k-units-J m , whereas the competitive ratio of the randomizedon-line algorithm of (ii) still tends to 1 for $d = o(\sqrt{D})$
and k > 1; (iii) different processing times yield harder instances than identicalprocessing times. There is no 5/3 competitive deterministic on-linealgorithm for k-units-J m , whereas the competitive ratio of the randomizedon-line algorithm of (ii) still tends to 1 for $d = o(\sqrt{D})$ 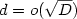 .
.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 2008
References
- 3
- Cited by

