Article contents
Palindromes in infinite ternary words
Published online by Cambridge University Press: 15 September 2009
Abstract
We study infinite words u over an alphabet $\mathcal{A}$  satisfying the property $\mathcal{P} :~\mathcal{P}(n)+\mathcal{P}(n+1) = 1+ \#\mathcal{A}\ {\rm for\ any}\ n \in\mathbb{N}$
satisfying the property $\mathcal{P} :~\mathcal{P}(n)+\mathcal{P}(n+1) = 1+ \#\mathcal{A}\ {\rm for\ any}\ n \in\mathbb{N}$ 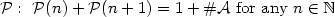 , where $\mathcal{P}(n)$
, where $\mathcal{P}(n)$ 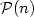 denotes the number ofpalindromic factors of length n occurring in the language of u.We study also infinite words satisfying a strongerproperty $\mathcal{PE}$
denotes the number ofpalindromic factors of length n occurring in the language of u.We study also infinite words satisfying a strongerproperty $\mathcal{PE}$ 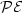 : every palindrome of u has exactly one palindromic extension in u. For binary words, the properties $\mathcal{P}$
: every palindrome of u has exactly one palindromic extension in u. For binary words, the properties $\mathcal{P}$ 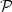 and $\mathcal{PE}$
and $\mathcal{PE}$ 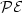 coincide and these properties characterize Sturmian words, i.e.,words with the complexity C(n) = n + 1 for any $n \in \mathbb{N}$
coincide and these properties characterize Sturmian words, i.e.,words with the complexity C(n) = n + 1 for any $n \in \mathbb{N}$ 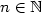 . In this paper, we focus on ternary infinite wordswith the language closed under reversal. For such words u,we prove that if C(n) = 2n + 1 for any $n \in \mathbb{N}$
. In this paper, we focus on ternary infinite wordswith the language closed under reversal. For such words u,we prove that if C(n) = 2n + 1 for any $n \in \mathbb{N}$ 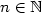 ,then u satisfies the property $\mathcal{P}$
,then u satisfies the property $\mathcal{P}$ 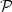 andmoreover u is rich in palindromes. Also a sufficient condition for the property $\mathcal{PE}$
andmoreover u is rich in palindromes. Also a sufficient condition for the property $\mathcal{PE}$ 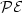 is given.We construct a word demonstrating that $\mathcal{P}$
is given.We construct a word demonstrating that $\mathcal{P}$ 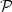 on a ternaryalphabet does not imply $\mathcal{PE}$
on a ternaryalphabet does not imply $\mathcal{PE}$ 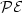 .
.
Information
- Type
- Research Article
- Information
- RAIRO - Theoretical Informatics and Applications , Volume 43 , Issue 4 , October 2009 , pp. 687 - 702
- Copyright
- © EDP Sciences, 2009
References
- 2
- Cited by

