Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:26:32.041Z Has data issue: false hasContentIssue false
  • English
  • Français

State complexity of cyclic shift

Published online by Cambridge University Press:  13 December 2007

Galina Jirásková  and
Alexander Okhotin
Galina Jirásková
Affiliation:
Mathematical Institute, Slovak Academy of Sciences, Grešákova 6, 040 01 Košice, Slovakia; jiraskov@saske.sk
Alexander Okhotin
Affiliation:
Academy of Finland Department of Mathematics, University of Turku, Turku 20014, Finland; alexander.okhotin@utu.fi
Get access

Abstract

The cyclic shift of a language L, defined as SHIFT(L) = {vu | uv ∈ L}, is an operation known to preserve both regularity and context-freeness. Its descriptional complexity has been addressed in Maslov's pioneering paper on the state complexity of regular language operations [Soviet Math. Dokl.11 (1970) 1373–1375], where a high lower bound for partial DFAs using a growing alphabet was given. We improve this result by using a fixed 4-letter alphabet, obtaining a lower bound (n-1)! . 2(n-1)(n-2), which shows that the state complexity of cyclic shift is 2n2+ nlogn - O(n) for alphabets with at least 4 letters. 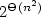For 2- and 3-letter alphabets, we prove $2^{\Theta(n^2)}$ state complexity. We also establish a tight 2n2+1 lower bound for the nondeterministic state complexity of this operation using a binary alphabet.

Keywords

Finite automatadescriptional complexitycyclic shift
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 2 , April 2008 , pp. 335 - 360
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A.V. Aho, J.D. Ullman and M. Yannakakis, On notions of information transfer in VLSI circuits, in Proceedings of 15th ACM STOC, ACM (1983) 133–139.
Birget, J.-C., Intersection and union of regular languages and state complexity. Inform. Process. Lett. 43 (1992) 185–190. CrossRef
Birget, J.-C., Partial orders on words, minimal elements of regular languages, and state complexity. Theor. Comput. Sci. 119 (1993) 267–291. CrossRef
Birget, J.-C., The state complexity of $\overline{\Sigma^*\overline{L}}$ and its connection with temporal logic. Inform. Process. Lett. 58 (1996) 185–188. CrossRef
Câmpeanu, C., Salomaa, K. and Tight, S. Yu lower bound for the state complexity of shuffle of regular languages. J. Autom. Lang. Comb. 7 (2002) 303–310.
Domaratzki, M., State complexity and proportional removals. J. Autom. Lang. Comb. 7 (2002) 455–468.
Domaratzki, M., Kisman, D. and Shallit, J., On the number of distinct languages accepted by finite automata with n states. J. Autom. Lang. Comb. 7 (2002) 469–486.
Geffert, V., Magic numbers in the state hierarchy of finite automata, Mathematical Foundations of Computer Science, MFCS 2006, Stará Lesná, Slovakia, August 28–September 1, 2006, Springer, Berlin. Lect. Notes Comput. Sci. 4162 (2006) 312–423.
Glaister, I. and Shallit, J., A lower bound technique for the size of nondeterministic finite automata. Inform. Process. Lett. 59 (1996) 75–77. CrossRef
Holzer, M. and Kutrib, M., Nondeterministic descriptional complexity of regular languages. Int. J. Found. Comput. Sci. 14 (2003) 1087–1102. CrossRef
J.E. Hopcroft and J.D. Ullman, Introduction to Automata Theory, Languages and Computation. Addison-Wesley (1979).
M. Hricko, G. Jirásková and A. Szabari, Union and intersection of regular languages and descriptional complexity, in Proceedings of DCFS 2005, Como, Italy, June 30–July 2, 2005, 170–181.
J. Hromkovič, Communication Complexity and Parallel Computing. Springer-Verlag, Berlin, Heidelberg (1997).
Hromkovič, J., Descriptional complexity of finite automata: concepts and open problems. J. Autom. Lang. Comb. 7 (2002) 519–531.
K. Iwama, A. Matsuura and M. Paterson, A family of NFAs which need 2n - α deterministic states. Theor. Comput. Sci. 301 (2003), 451–462.
Jirásková, G., State complexity of some operations on binary regular languages. Theor. Comput. Sci. 330 (2005) 287–298. CrossRef
Maslov, A.N., Estimates of the number of states of finite automata. Soviet Mathematics Doklady 11 (1970) 1373–1375.
Maslov, A.N., Cyclic shift operation for languages. Probl. Inf. Transm. 9 (1973) 333–338.
Oshiba, T., Closure property of the family of context-free languages under the cyclic shift operation. T. IECE 55D (1972) 119–122.
Salomaa, A., Wood, D. and On, S. Yu the state complexity of reversals of regular languages. Theor. Comput. Sci. 320 (2004) 315–329. CrossRef
Salomaa, A., Salomaa, K. and State, S. Yu complexity of combined operations. Theor. Comput. Sci. 383 (2007) 140–152. CrossRef
State, S. Yu complexity: recent results and open problems. Fund. Inform. 64 (2005) 471–480.
Yu, S., Zhuang, Q. and Salomaa, K., The state complexity of some basic operations on regular languages. Theor. Comput. Sci. 125 (1994) 315–328. CrossRef
van Zijl, L., Magic numbers for symmetric difference NFAs. Int. J. Found. Comput. Sci. 16 (2005) 1027–1038. CrossRef