Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-11T00:21:50.408Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLETENESS FOR COUNTER-DOXA CONDITIONALS – USING RANKING SEMANTICS

Published online by Cambridge University Press:  30 October 2018

ERIC RAIDL
ERIC RAIDL*
Affiliation:
Department of Philosophy, University of Konstanz
*
*DEPARTMENT OF PHILOSOPHY UNIVERSITY OF KONSTANZ POSTFACH D6, 78457 KONSTANZ, GERMANY E-mail: eric.3.raidl@uni-konstanz.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Standard conditionals 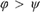$\varphi > \psi$, by which I roughly mean variably strict conditionals à la Stalnaker and Lewis, are trivially true for impossible antecedents. This article investigates three modifications in a doxastic setting. For the neutral conditional, all impossible-antecedent conditionals are false, for the doxastic conditional they are only true if the consequent is absolutely necessary, and for the metaphysical conditional only if the consequent is ‘model-implied’ by the antecedent. I motivate these conditionals logically, and also doxastically by properties of conditional belief and belief revision. For this I show that the Lewisian hierarchy of conditional logics can be reproduced within ranking semantics, provided we slightly stretch the notion of a ranking function. Given this, acceptance of a conditional can be interpreted as a conditional belief. The epistemic and the neutral conditional deviate from Lewis’ weakest system 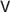$V$, in that ID (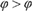$\varphi > \varphi$) or even CN (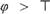$\varphi > \top$) are dropped, and new axioms appear. The logic of the metaphysical conditional is completely axiomatised by 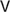$V$ to which we add the known Kripke axioms T5 for the outer modality. Related completeness results for variations of the ranking semantics are obtained as corollaries.

Keywords

03A0503B4503B4203B4703B6568T3791F20conditionalsconditionalisationranking theoryranking semanticscounter-possiblesvacuismnonvacuism
Type
Research Article
Information
The Review of Symbolic Logic , Volume 12 , Issue 4 , December 2019 , pp. 861 - 891
Copyright
Copyright © Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Alchourrón, C. E., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. Journal of Symbolic Logic, 50, 510–530.CrossRefGoogle Scholar
Berto, F., French, R., Priest, G., & Ripley, D. (2018). Williamson on counterpossibles. Journal of Philosophical Logic, 47(4), 693–713.CrossRefGoogle ScholarPubMed
Burgess, J. (1981). Quick completeness proofs for some logics of conditionals. Notre Dame Journal of Formal Logic, 22, 76–84.CrossRefGoogle Scholar
Bjerring, J. C. (2014). On counterpossibles. Philosophical Studies, 168, 327–353.CrossRefGoogle Scholar
Brogaard, B. & Salerno, J. (2013). Remarks on counterpossibles. Synthese, 190, 639–660.CrossRefGoogle Scholar
Chellas, B. F. (1975). Basic conditional logic. Journal of Philosophical Logic, 4, 133–153.CrossRefGoogle Scholar
Darwiche, A. & Pearl, J. (1997). On the logic of iterated belief revision. Artificial Intelligence, 89(1–2), 1–29.CrossRefGoogle Scholar
Fine, K. (1975). Review of counterfactuals. Mind, 84, 451–458.CrossRefGoogle Scholar
Friedman, N. & Halpern, J. (2001). Plausibility measures and default reasoning. Journal of the Association for Computing Machinery, 48(4), 648–685.CrossRefGoogle Scholar
Gärdenfors, P. (1982). Imaging and conditionalization. The Journal of Philosophy, 79(12), 747–760.CrossRefGoogle Scholar
Goldszmidt, M. & Pearl, J. (1996). Qualitative probabilities for default reasoning, belief revision, and causal modelling. Artificial Intelligence, 84, 57–112.CrossRefGoogle Scholar
Halpern, J. (2003). Reasoning About Uncertainty. Cambridge, MA: MIT Press.Google Scholar
Huber, F. (2006). Ranking functions and rankings on languages. Artificial Intelligence, 170, 462–471.CrossRefGoogle Scholar
Huber, F. (2007a). The logic of theory assessment. Journal of Philosophical Logic, 36, 511–538.CrossRefGoogle Scholar
Huber, F. (2007b). The consistency argument for ranking functions. Studia Logica, 86(2), 299–329.CrossRefGoogle Scholar
Huber, F. (2014). New foundations for counterfactuals. Synthese, 91, 2167–2193.CrossRefGoogle Scholar
Huber, F. (2015). What should I believe about what would have been the case? Journal of Philosophical Logic, 44, 81–110.CrossRefGoogle Scholar
Huber, F. (2017). Why follow the royal rule? Synthese, 194(5), 1565–1590.CrossRefGoogle Scholar
Kment, B. (2014). Modality and Explanatory Reasoning. Oxford: Oxford University Press.CrossRefGoogle Scholar
Lauer, S. (2017). ‘I believe’ in a ranking-theoretic analysis of ‘believe’. In van Gessel, T. and Roelofsen, F., editors. Proceedings of the 21st Amsterdam Colloquium. Amsterdam: ILLC, pp. 335–344.Google Scholar
Lewis, D. (1971). Completeness and decidability of three logics of counterfactual conditionals. Theoria, 37(1), 74–85.CrossRefGoogle Scholar
Lewis, D. (1973). Counterfactuals and comparative possibility. Journal of Philosophical Logic, 2, 418–446.CrossRefGoogle Scholar
Loewer, B. M. (1979). Cotenability and counterfactual logics. Journal of Philosophical Logic, 8(1), 99–115.CrossRefGoogle Scholar
Mares, E. D. & Fuhrmann, A. (1995). A relevant theory of conditionals. Journal of Philosophical Logic, 24, 645–665.CrossRefGoogle Scholar
Mayer, J. C. (1981). A misplaced thesis of conditional logic. Journal of Philosophical Logic, 10(2), 235–238.CrossRefGoogle Scholar
Nolan, D. (1997). Impossible worlds: A modest approach. Notre Dame Journal of Formal Logic, 38, 535–572.Google Scholar
Raidl, E. (2018). Ranking semantics for doxastic necessities and conditionals. In Pavel, A. & Lávička, T., editors. Logica Yearbook 2017. London: College Publications, pp. 223–238.Google Scholar
Raidl, E. & Skovgaard-Olsen, N. (2017). Simulating Lewis/Stalnaker Conditionals in Ranking Theory. Unpublished manuscript.Google Scholar
Spohn, W. (1988). Ordinal conditional functions. A dynamic theory of epistemic states. In Harper, W. L. and Skyrms, B. editors. Causation in Decision, Belief Change, and Statistics, Vol. 2. Dordrecht: Kluwer, pp. 105–134.CrossRefGoogle Scholar
Spohn, W. (2012). The Laws of Belief: Ranking Theory and its Philosophical Applications. Oxford: Oxford University Press.CrossRefGoogle Scholar
Spohn, W. (2015). Conditionals: A unifying ranking-theoretic perspective. Philosopher’s Imprint, 15(1), 1–30.Google Scholar
Unterhuber, M. (2016). Beyond system P – Hilbert-Style convergence results for conditional logics with a connexive twist. IFCoLog Journal of Logics and their Application, 3(3), 376–412.Google Scholar
Williamson, T. (2007). The philosophy of philosophy. Oxford: Oxford University Press.CrossRefGoogle Scholar
Williamson, T. (2018). Counterpossibles. Topoi, 37(3), 357–368.CrossRefGoogle Scholar