No CrossRef data available.
Article contents
DECIDABILITY OF INDEPENDENCE-FRIENDLY MODAL LOGIC
Published online by Cambridge University Press: 13 July 2010
Abstract
In this paper we consider an independence-friendly modal logic, IFML. It follows from results in the literature that qua expressive power, IFML is a fragment of second-order existential logic, 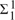 , that cannot be translated into first-order logic. It is also known that IFML lacks the tree structure property. We show that IFML has the ‘truncated structure property’, a weaker version of the tree structure property, and that its satisfiability problem is solvable in 2NEXP. This implies that this paper reveals a new decidable fragment of
, that cannot be translated into first-order logic. It is also known that IFML lacks the tree structure property. We show that IFML has the ‘truncated structure property’, a weaker version of the tree structure property, and that its satisfiability problem is solvable in 2NEXP. This implies that this paper reveals a new decidable fragment of  . We also show that IFML becomes undecidable if we add the identity symbol to its vocabulary by means of a reduction from the tiling problem.
. We also show that IFML becomes undecidable if we add the identity symbol to its vocabulary by means of a reduction from the tiling problem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010

