Article contents
THE FINE STRUCTURE OF THE INTUITIONISTIC BOREL HIERARCHY
Published online by Cambridge University Press: 01 March 2009
Abstract
In intuitionistic analysis, a subset of a Polish space like ℝ or 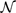 is called positively Borel if and only if it is an open subset of the space or a closed subset of the space or the result of forming either the countable union or the countable intersection of an infinite sequence of (earlier constructed) positively Borel subsets of the space. The operation of taking the complement is absent from this inductive definition, and, in fact, the complement of a positively Borel set is not always positively Borel itself (see Veldman, 2008a). The main result of Veldman (2008a) is that, assuming Brouwer's Continuity Principle and an Axiom of Countable Choice, one may prove that the hierarchy formed by the positively Borel sets is genuinely growing: every level of the hierarchy contains sets that do not occur at any lower level. The purpose of the present paper is a different one: we want to explore the truly remarkable fine structure of the hierarchy. Brouwer's Continuity Principle again is our main tool. A second axiom proposed by Brouwer, his Thesis on Bars is also used, but only incidentally.
is called positively Borel if and only if it is an open subset of the space or a closed subset of the space or the result of forming either the countable union or the countable intersection of an infinite sequence of (earlier constructed) positively Borel subsets of the space. The operation of taking the complement is absent from this inductive definition, and, in fact, the complement of a positively Borel set is not always positively Borel itself (see Veldman, 2008a). The main result of Veldman (2008a) is that, assuming Brouwer's Continuity Principle and an Axiom of Countable Choice, one may prove that the hierarchy formed by the positively Borel sets is genuinely growing: every level of the hierarchy contains sets that do not occur at any lower level. The purpose of the present paper is a different one: we want to explore the truly remarkable fine structure of the hierarchy. Brouwer's Continuity Principle again is our main tool. A second axiom proposed by Brouwer, his Thesis on Bars is also used, but only incidentally.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2009
References
BIBLIOGRAPHY
- 2
- Cited by

