Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T03:42:01.068Z Has data issue: false hasContentIssue false
  • English
  • Français

FREGE’S CONSTRAINT AND THE NATURE OF FREGE’S FOUNDATIONAL PROGRAM

Published online by Cambridge University Press:  05 December 2018

MARCO PANZA  and
ANDREA SERENI
MARCO PANZA*
Affiliation:
CNRS, IHPST, Paris (CNRS and University of Paris 1, Panthéon-Sorbonne), Chapman University
ANDREA SERENI*
Affiliation:
Scuola Universitaria Superiore IUSS Pavia
*
*CNRS, IHPST 13 RUE DU FOUR PARIS 75006, FRANCE (CNRS AND UNIV. PARIS 1, PANTHÉON-SORBONNE), E-mail: marco.panza@univ-paris1.fr and CHAPMAN UNIVERSITY ONE UNIVERSITY DRIVE ORANGE, CA 92866, USA E-mail: panza@chapman.edu
†SCUOLA UNIVERSITARIA SUPERIORE IUSS PAVIA NETS CENTER PIAZZA DELLA VITTORIA, 15 27100 PAVIA, ITALY E-mail: andrea.sereni@iusspavia.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent discussions on Fregean and neo-Fregean foundations for arithmetic and real analysis pay much attention to what is called either ‘Application Constraint’ (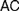$AC$) or ‘Frege Constraint’ (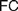$FC$), the requirement that a mathematical theory be so outlined that it immediately allows explaining for its applicability. We distinguish between two constraints, which we, respectively, denote by the latter of these two names, by showing how 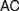$AC$ generalizes Frege’s views while 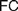$FC$ comes closer to his original conceptions. Different authors diverge on the interpretation of 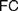$FC$ and on whether it applies to definitions of both natural and real numbers. Our aim is to trace the origins of 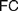$FC$ and to explore how different understandings of it can be faithful to Frege’s views about such definitions and to his foundational program. After rehearsing the essential elements of the relevant debate (§1), we appropriately distinguish 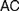$AC$ from 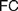$FC$ (§2). We discuss six rationales which may motivate the adoption of different instances of 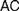$AC$ and 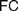$FC$ (§3). We turn to the possible interpretations of 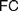$FC$ (§4), and advance a Semantic 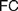$FC$ (§4.1), arguing that while it suits Frege’s definition of natural numbers (4.1.1), it cannot reasonably be imposed on definitions of real numbers (§4.1.2), for reasons only partly similar to those offered by Crispin Wright (§4.1.3). We then rehearse a recent exchange between Bob Hale and Vadim Batitzky to shed light on Frege’s conception of real numbers and magnitudes (§4.2). We argue that an Architectonic version of 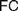$FC$ is indeed faithful to Frege’s definition of real numbers, and compatible with his views on natural ones. Finally, we consider how attributing different instances of $FC$ to Frege and appreciating the role of the Architectonic 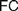$FC$ can provide a more perspicuous understanding of his foundational program, by questioning common pictures of his logicism (§5).

Keywords

00A3003A0503A10Frege’s Constraintapplicability of mathematicsFrege’s foundational programlogicism
Type
Research Article
Information
The Review of Symbolic Logic , Volume 12 , Issue 1 , March 2019 , pp. 97 - 143
Copyright
Copyright © Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Batitsky, V. (2002). Some measurement-theoretic concerns about Hale’s ‘Reals by Abstraction’. Philosophia Mathematica, 10(3), 286–303.CrossRefGoogle Scholar
Benacerraf, P. (1965). What numbers could not be. Philosophical Review, 74(1), 47–73.CrossRefGoogle Scholar
Benacerraf, P. (1981). Frege: The last logicist. Midwest Studies in Philosophy, 6(1), 17–36.CrossRefGoogle Scholar
Boccuni, F. & Panza, M. (Manuscript). On the logicality of Frege’s definition of real numbers.Google Scholar
Currie, G. (1986). Continuity and change in Frege’s philosophy of mathematics. In Haaparanta, L. and Hintikka, J., editors. Frege Synthetisized. Esays on the Philosophical and Foundational Work of Gottlob Frege. Dordrecht, Boston, Lancaster, Tokyo: D. Reidel, pp. 345–373.Google Scholar
Dedekind, R. (1888). Was sind und was sollen die Zahlen. Braunschweig: F. Vieweg und Sohn. Also in Dedekind, R. (1930–1932). Gesammelte Mathematische Werke (Herausgegeben, E. N. von, Fricke, R., and Ore, Ö., editors), Vol. 3. Braunschweig: Vieweg, Chapter LI, 335–391.Google Scholar
Díez, J. A. (1997). A hundred years of numbers. An historical introduction to measurement theory 1887–1990. Studies in History and Philophy of Sciences, 28, 167–185, 237–265.CrossRefGoogle Scholar
Dummett, M. (1991). Frege. Philosophy of Mathematics. Cambridge (Massachusetts): Harvard University Press.Google Scholar
Frege, G. (1884). Die Grundlagen der Arithmetik. Eine Logische Mathematische Untersuchung über den Begriff der Zahl. Breslau: Verrlag von W. Koebner.Google Scholar
Frege, G. (1893–1903). Die Grundgesetze der Arithmetick, Vol. I–II. Jena: Hermann Pohle.Google Scholar
Frege, G. (1903). Über die Grundlagen der Geometrie. Jahresbericht der Deutschen Mathematiker-Vereinigung, 12, 319–324, 368–375.Google Scholar
Frege, G. (1950). The Foundations of Arithmetic. A logico-mathematical enquiry into the concept of number (Translated by Austin, J. L., second revised edition). New York: Harper & Brothers.Google Scholar
Frege, G. (1971). On the Foundations of Geometry and Formal Theories of Arithmetic. Edited and translated by Kluge, E.-H. W. New Haven: Yale University Press.Google Scholar
Frege, G. (1976). Nachgelassene Schriften und Wissenschaftlicher Briefwechsel (Hermes, H., Kambartel, H., and Kaulbach, F., editors). Hamburg: Felix Meiner Verlag.Google Scholar
Frege, G. (2013). Basic Laws of Arithmetic. Tranlated and edited by Ebert, P. A. and Rossberg, M. with Wright, C.. Oxford: Oxford University Press.Google Scholar
Gandon, S. (2012). Russell’s Unknown Logicism. Palgrave MacMillan.CrossRefGoogle Scholar
Gauss, C. F. (1831). Announcement of the Commentatio secunda to the Theoria residuorum biquadraticorum. Gottingische gelehrte Anzeigen, 1, 625–638. Also in Gauss, C. F. (1863–1917). Werke, Vol. 2. Herausgegeben von der Königlichen Gesellchaft der Wissenschaften zu Göttingen. Göttingen: Dietrich, pp. 169–178.Google Scholar
Goldfarb, W. (2001). Frege’s conception of logic. In Floyd, J. and Shieh, S., editors. Future Pasts: The Analytic Tradition in Twentieth-Century Philosophy, Oxford, New York: Oxford University Press, pp. 25–41.CrossRefGoogle Scholar
Hale, B. (2000). Reals by abstraction. Philosophia Mathematica (III), 8, 100–123.CrossRefGoogle Scholar
Hale, B. (2002). Real numbers, quantities, and measurement. Philosophia Mathematica, 10(3), 304–323.CrossRefGoogle Scholar
Hale, B. (2016). Definitions of numbers and their applications. In Ebert, P. A. and Rossberg, M., editors. Abstractionism: Essays in Philosophy of Mathematics, Oxford, New York: Oxford University Press, pp. 332–349.CrossRefGoogle Scholar
Hankel, H. (1687). Theorie der Complexen Zahlensysteme […]. Theil I der Vorlesugen über die Complexen Zahlen […] in Zwei Theilen. Leipzig: Leopold Voss.Google Scholar
Helmholtz, H. (1868). Ueber die Thatsachen, die der Geometrie zum Grunde liegen. Nachrichten von der Königlichen Gesellschaft der Wissenschaften […], 9, Juni 3, pp. 193–221.Google Scholar
Helmoltz, H. v. (1887). Zählen und Messen, erkenntnisstheoretisch betrachtet. In Philosophische Aufsätze, Eduard Zeller zu seinem fünfzigjährigen Doctorjubiläum gewidmet, Leipzig: Fues’ Verlag, pp. 17–52.Google Scholar
Hölder, O. (1901). Die axiome der quantität und die lehre vom mass. Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, mathematisch-physischen Classe, 53, 1–64.Google Scholar
Jeshion, R. (2001). Frege’s notions of self-evidence. Mind, 110(440), 937–976.CrossRefGoogle Scholar
Kant, I. (1998). Critique of Pure Reason. Cambridge: Cambridge University Press. Tranlated and edited by Guyer, P. and Wood, A. W..CrossRefGoogle Scholar
Kitcher, P. (1979). Frege’s epistemology. Philosophical Review, 88(2), 235–262.CrossRefGoogle Scholar
Krantz, D. H., Luce, R. D., Suppes, P., & Tversky, A. (1971–1990). Foundations of Measurement , Vol. 3. New York: Acedemic Press.Google Scholar
Kutschera, F. v. (1966). Freges begründung der analysis. Archiv für mathematische Logik und Grundlagenforschung, 9, 102–111.CrossRefGoogle Scholar
MacFarlane, J. (2002). Frege, Kant, and the logic in logicism. The Philosophical Review, 111(1), 25–65.CrossRefGoogle Scholar
McCallion, P. (2016). On Frege‘s applications constraint. In Ebert, P. A. and Rossberg, M., editors. Abstractionism: Essays in Philosophy of Mathematics. Oxford, New York: Oxford University Press, pp. 311–322.CrossRefGoogle Scholar
Menge, H. (editor) (1846). Euclidis Data. Lipsiæ: B. G. Tuebneri.Google Scholar
Mill, J. S. (1872). A System Of Logic, Ratiocinative And Inductive […], Eight Edition, Vol. 2. London: Longmans, Green, Reader, and Dyer.Google Scholar
Mill, J. S. (1877). System der Deductiven und Inductiven Logik […]. In’s Deutsche überetragen von J. Schiel. Vierte deutsche nach der Achten des Originals erweiterte Auflage, Vol. 2. Braunschweig: Friedrich Vieweg und Sohn.Google Scholar
Panza, M. (2016). Abstraction and epistemic economy. In Costreie, S., editor. Early Analytic Philosophy. New Perspective on the Tradition, Springer, Cham, Heidelberg, pp. 387–428.Google Scholar
Panza, M. (2018). Was Frege a logicist for arithmetic. In Coliva, A., Leonardi, P., and Moruzzi, S., editors. Eva Picardi on Language, Analysis and History. London, New York: Palgrave Macmillan, pp. 87–112.CrossRefGoogle Scholar
Peacocke, C. (2015). Magnitudes: Metaphysics, explanation, and perception. In Moyal-Sharrock, D., Munz, V., and Coliva, A., editors. Mind, Language and Action: Proceedings of the 36th International Wittgenstein Symposium, Berlin, Munich, Boston: De Gruyter, pp. 357–387.Google Scholar
Riemann, B (1866–1867). Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. Abhandlungen der Königlichen Gesellshaft der Wissenshaften zu Göttingen, 13, 133–150.Google Scholar
Riemann, B. (2016). Bernhard Riemann. On the Hypotheses Which Lie at the Bases of Geometry. Switzerland: Birkhäuser, Springer International Publishing. Edited by Jost, Jürgen.CrossRefGoogle Scholar
Russell, B. (1903). The Principles of Mathematics. Cambridge: Cambridge University Press.Google Scholar
Russell, B. & Whitehead, A. N. (1910–1913). Principia Mathematica, Vol. 3. Cambridge: Cambridge University Press.Google Scholar
Sereni, A. (manuscript). On the Philosophical Significance of Frege’s Constraint.Google Scholar
Shapiro, S. (1997). Philosophy of Mathematics: Structure and Ontology, Vol.2. Oxford: Oxford University Press.Google Scholar
Shapiro, S. (2000). Frege meets dedekind: A Neologicist treatment of real analysis. Notre Dame Journal of Formal Logic, 4, 317–421.Google Scholar
Shapiro, S. (2009). We hold these truths to be self-evident: But what do we mean by that? Review of Symbolic Logic, 2(1), 175–207.CrossRefGoogle Scholar
Simons, P. (1987). Frege’s theory of real numbers. History and Philosophy of Logic, 8, 25–44. Also in Demopoulos, W. (1995). Frege’s Philosopjy of Mathematics. Cambridge, MA: Harvard University Press, pp. 358–383.Google Scholar
Snyder, E., Samuels, R., & Shapiro, S. (2018). Neologicism, Frege’s constraint, and the Frege-Heck condition. Noûs, doi: 10.1111/nous.12249.CrossRefGoogle Scholar
Steiner, M. (1998). The Applicability of Mathematics as a Philosophical Problem. Cambridge (Massachusetts): Harvard University Press.Google Scholar
Steiner, M. (2005). Mathematics: Application and applicability. In Shapiro, S., editor. Oxford Handbook of the Philosophy of Mathematics and Logic, Oxford, New York: Oxford University Press, pp. 625–650.CrossRefGoogle Scholar
Taisbak, C. M. (2003). ΔEΔOMENA. Euclid’s Data or The Importance of Being Given. Copenhagen: Museaum Tusculanum Press.Google Scholar
Weiner, J. (1984). The philosopher behind the last lsogicist. Philosophical Quarterly, 34(136), 242–264.CrossRefGoogle Scholar
Weiner, J. (1990). Frege in Perspective. Cornell University Press.Google Scholar
Wright, C. (2000). Neo-Fregean foundations for real analysis: Some reflections on Frege’s constraint. Notre Dame Journal of Formal Logic, 41(4), 317–334.Google Scholar