No CrossRef data available.
Article contents
LOGICS ABOVE S4 AND THE LEBESGUE MEASURE ALGEBRA
Published online by Cambridge University Press: 28 October 2016
Abstract
We study the measure semantics for propositional modal logics, in which formulas are interpreted in the Lebesgue measure algebra 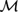 ${\cal M}$ , or algebra of Borel subsets of the real interval [0,1] modulo sets of measure zero. It was shown in Lando (2012) and Fernández-Duque (2010) that the propositional modal logic S4 is complete for the Lebesgue measure algebra. The main result of the present paper is that every logic L aboveS4 is complete for some subalgebra of
${\cal M}$ , or algebra of Borel subsets of the real interval [0,1] modulo sets of measure zero. It was shown in Lando (2012) and Fernández-Duque (2010) that the propositional modal logic S4 is complete for the Lebesgue measure algebra. The main result of the present paper is that every logic L aboveS4 is complete for some subalgebra of 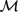 ${\cal M}$ . Indeed, there is a single model over a subalgebra of
${\cal M}$ . Indeed, there is a single model over a subalgebra of 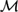 ${\cal M}$ in which all nontheorems of L are refuted. This work builds on recent work by Bezhanishvili, Gabelaia, & Lucero-Bryan (2015) on the topological semantics for logics above S4. In Bezhanishvili et al., (2015), it is shown that there are logics above that are not the logic of any subalgebra of the interior algebra over the real line,
${\cal M}$ in which all nontheorems of L are refuted. This work builds on recent work by Bezhanishvili, Gabelaia, & Lucero-Bryan (2015) on the topological semantics for logics above S4. In Bezhanishvili et al., (2015), it is shown that there are logics above that are not the logic of any subalgebra of the interior algebra over the real line, 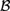 ${\cal B}$ (ℝ), but that every logic above is the logic of some subalgebra of the interior algebra over the rationals,
${\cal B}$ (ℝ), but that every logic above is the logic of some subalgebra of the interior algebra over the rationals, 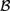 ${\cal B}$ (ℚ), and the interior algebra over Cantor space,
${\cal B}$ (ℚ), and the interior algebra over Cantor space, 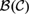 ${\cal B}\left( {\cal C} \right)$ .
${\cal B}\left( {\cal C} \right)$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2016

