Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-11T07:18:39.509Z Has data issue: false hasContentIssue false
  • English
  • Français

LOGICS FOR PROPOSITIONAL DETERMINACY AND INDEPENDENCE

Published online by Cambridge University Press:  02 April 2018

VALENTIN GORANKO  and
ANTTI KUUSISTO
VALENTIN GORANKO*
Affiliation:
Department of Philosophy, Stockholm University Department of Mathematics, University of Johannesburg (visiting professorship)
ANTTI KUUSISTO*
Affiliation:
FB03: Mathematics/Computer Science, University of Bremen
*
*DEPARTMENT OF PHILOSOPHY STOCKHOLM UNIVERSITY STOCKHOLM, SWEDEN and DEPARTMENT OF MATHEMATICS UNIVERSITY OF JOHANNESBURG (VISITING PROFESSORSHIP) JOHANNESBURG, SOUTH AFRICA E-mail: valentin.goranko@philosophy.su.se
†FB03: MATHEMATICS/COMPUTER SCIENCE UNIVERSITY OF BREMEN BREMEN, GERMANY E-mail:antti.j.kuusisto@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates formal logics for reasoning about determinacy and independence. Propositional Dependence Logic 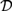${\cal D}$ and Propositional Independence Logic 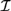${\cal I}$ are recently developed logical systems, based on team semantics, that provide a framework for such reasoning tasks. We introduce two new logics 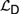${{\cal L}_D}$ and 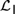${{\cal L}_{\,I\,}}$, based on Kripke semantics, and propose them as alternatives for 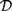${\cal D}$ and ${\cal I}$, respectively. We analyse the relative expressive powers of these four logics and discuss the way these systems relate to natural language. We argue that 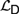${{\cal L}_D}$ and 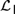${{\cal L}_{\,I\,}}$ naturally resolve a range of interpretational problems that arise in 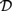${\cal D}$ and 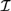${\cal I}$. We also obtain sound and complete axiomatizations for 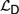${{\cal L}_D}$ and 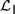${{\cal L}_{\,I\,}}$.

Keywords

03A0503B4503B6003B65determinancydependenceteam semanticsmodal logicnatural language
Type
Research Article
Information
The Review of Symbolic Logic , Volume 11 , Issue 3 , September 2018 , pp. 470 - 506
Copyright
Copyright © Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This document and all that is needed to prepare documents for ASL publications are posted in the ASL Typesetting Office Website, http://www.math.ucla.edu/∼asl/asltex. August 20, 2000.

References

BIBLIOGRAPHY

Aloni, M. (2016). Disjunction. In Zalta, E. N., editor. The Stanford Encyclopedia of Philosophy. Stanford: Stanford University. Available at: https://plato.stanford.edu/archives/win2016/entries/disjunction/.Google Scholar
Armstrong, W. (1974). Dependency structures of database relationships. In Rosenfeld, J. L., editor. IFIP’74. Amsterdam, The Netherlands: North-Holland, pp. 580–583.Google Scholar
Ciardelli, I. (2009). Inquisitive Semantics and Intermediate Logics. Master’s Thesis, University of Amsterdam.Google Scholar
Ciardelli, I. (2016). Dependency as question entailment. In Väänänen, J., Abramsky, S., Kontinen, J., and Vollmer, H., editors. Dependence Logic: Theory and Applications. Switzerland: Springer International Publishing, pp. 129–181.CrossRefGoogle Scholar
Ciardelli, I. (2016). Questions in Logic. Ph.D. Thesis, University of Amsterdam.Google Scholar
Ciardelli, I. & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40(1), 55–94.CrossRefGoogle Scholar
Ciardelli, I. & Roelofsen, F. (2015). Inquisitive dynamic epistemic logic. Synthese, 192(6), 1643–1687.CrossRefGoogle Scholar
Demri, S. (1997). A completeness proof for a logic with an alternative necessity operator. Studia Logica, 58(1), 99–112.CrossRefGoogle Scholar
Fan, J. (2016). A modal logic of supervenience. Preprint, arXiv:1611.04740v1.Google Scholar
Fan, J., Wang, Y., & van Ditmarsch, H. (2015). Contingency and knowing whether. Review of Symbolic Logic, 8(1), 75 –107.CrossRefGoogle Scholar
Galliani, P. (2012). Inclusion and exclusion dependencies in team semantics - on some logics of imperfect information. Annals of Pure and Applied Logic, 163(1), 68–84.CrossRefGoogle Scholar
Galliani, P. (2013). Epistemic operators in dependence logic. Studia Logica, 101(2), 367–397.CrossRefGoogle Scholar
Galliani, P. & Väänänen, J. (2014). On dependence logic. In Baltag, A. and Smets, S., editors. Johan F. A. K. van Benthem on Logical and Informational Dynamics. Berlin: Springer, pp. 101–119.Google Scholar
Goranko, V. & Kuusisto, A. (2016). Logics for propositional determinacy and independence. Preprint, arXiv:1609.07398.Google Scholar
Goranko, V. & Passy, S. (1992). Using the universal modality: Gains and questions. Journal of Logic and Computation, 2(1), 5–30.CrossRefGoogle Scholar
Grädel, E. & Väänänen, J. (2013). Dependence and independence. Studia Logica, 101(2), 399–410.CrossRefGoogle Scholar
Grelling, K. (1939). A logical theory of dependence. Proceedings of the 5th International Congress for the Unity of Science.Cambridge, MA. Reprinted in Smith, B. & von Ehrenfels, C. (1988). Foundations of Gestalt Theory. Philosophia Resources Library. Munich: Philosophia Verlag.Google Scholar
Hannula, M., Kontinen, J., Virtema, J., & Vollmer, H. (2015). Complexity of propositional independence and inclusion logic. In Italiano, G. F., Pighizzini, G., and Sannella, D. T., editors. MFCS 2015, Proceedings, Part I. Berlin: Springer, pp. 269–280.Google Scholar
Hella, L., Kuusisto, A., Meier, A., & Vollmer, H. (2015). Modal inclusion logic: Being lax is simpler than being strict. In Italiano, G. F., Pighizzini, G., and Sannella, D. T., editors. MFCS 2015, Proceedings, Part I. Berlin: Springer, pp. 281–292.Google Scholar
Hella, L., Luosto, K., Sano, K. & Virtema, J. (2014). The expressive power of modal dependence logic. In Goré, R., Kooi, B., and Kurucz, A., editors. AiML 10. London: College Publications, pp. 294–312.Google Scholar
Hintikka, J. (1996). The Principles of Mathematics Revisited. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Hintikka, J. & Sandu, G. (1989). Informational independence as a semantical phenomenon. In Fenstad, J. E., Frolov, I. T., and Hilpinen, R., editors. Logic, Methodology and Philosophy of Science, Vol. 8. Amsterdam: Elsevier, pp. 571–589.Google Scholar
Hodges, W. (1997). Compositional semantics for a language of imperfect information. Logic Journal of the IGPL, 5(4), 539–563.CrossRefGoogle Scholar
Humberstone, L. (1992). Some structural and logical aspects of the notion of supervenience. Logique et Analyse, 35, 101–137.Google Scholar
Humberstone, L. (1993). Functional dependencies, supervenience, and consequence relations. Journal of Logic, Language and Information, 2(4), 309–336.CrossRefGoogle Scholar
Humberstone, L. (1995). The logic of noncontingency. Notre Dame Journal of Formal Logic, 36(2), 214–229.Google Scholar
Humberstone, L. (1998). Note on supervenience and definability. Notre Dame Journal of Formal Logic, 39(2), 243–252.Google Scholar
Humberstone, L. (2002). The modal logic of agreement and noncontingency. Notre Dame Journal of Formal Logic, 43(2), 95–127.CrossRefGoogle Scholar
Humberstone, L. (2017). Supervenience, dependence, disjunction. Unpublished Manuscript.Google Scholar
Janssen, T. (1997). An overview of compositional translations. In Roever, W.-P. de, Langmaack, H., and Pnueli, A., editors. Compositionality: The Significant Difference, International Symposium, COMPOS’97. Berlin: Springer, pp. 327–349.Google Scholar
Kontinen, J. (2013). Dependence logic: A survey of some recent work. Philosophy Compass, 8(10), 950–963.CrossRefGoogle Scholar
Kontinen, J., Müller, J.-S., Schnoor, H., & Vollmer, H. (2014). Modal independence logic. In Goré, R., Kooi, B. P., and Kurucz, A., editors. AiML 10. London: College Publications, pp. 353–372.Google Scholar
Kontinen, J., Müller, J.-S., Schnoor, H., & Vollmer, H. (2015). A van Benthem theorem for modal team semantics. In Kreutzer, S., editor. CSL 2015. Dagstuhl: Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, pp. 277–291.Google Scholar
Kuusisto, A. (2014). A double team semantics for generalized quantifiers. Preprint, arXiv:1310.3032v5.Google Scholar
Kuusisto, A. (2015). A double team semantics for generalized quantifiers. Preprint, arXiv:1310.3032v8.Google Scholar
Kuusisto, A. (2015). A double team semantics for generalized quantifiers. Preprint, arXiv:1310.3032v9.Google Scholar
Lohmann, P. & Vollmer, H. (2013). Complexity results for modal dependence logic. Studia Logica, 101(2), 343–366.CrossRefGoogle Scholar
McLaughlin, B. & Bennett, K. (2018). Supervenience. In Zalta, E. N. editor. The Stanford Encyclopedia of Philosophy. Stanford: Stanford University. Available at: https://plato.stanford.edu/entries/supervenience/.Google Scholar
Montgomery, H. & Routley, R. (1966). Contingency and noncontingency bases for normal modal logics. Logique et Analyse, 9(35), 318–328.Google Scholar
Pizzi, C. (2007). Necessity and relative contingency. Studia Logica, 85(3), 395–410.CrossRefGoogle Scholar
Pizzi, C. (2013). Relative contingency and bimodality. Logica Universalis, 7(1), 113–123.CrossRefGoogle Scholar
Roelofsen, F. (2013). Algebraic foundations for the semantic treatment of inquisitive content. Synthese, 190(1), 79–102.CrossRefGoogle Scholar
Smith, B. & von Ehrenfels, C. (1988). Foundations of Gestalt Theory. Philosophia Resources Library. Munich: Philosophia Verlag.Google Scholar
Väänänen, J. (2007). Dependence Logic - a New Approach to Independence Friendly Logic. London Mathematical Society Student Texts, Vol. 70. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Väänänen, J. (2008). Modal dependence logic. In Apt, K. R. and van Rooij, R., editors. New Perspectives on Games and Interaction. Amsterdam, The Netherlands: Amsterdam University Press, pp. 237–254.Google Scholar
Yang, F. (2014). Extensions and Variants of Dependence Logic. Ph.D. Thesis, University of Helsinki.Google Scholar
Yang, F. (2016). Uniform definability in propositional dependence logic. Preprint, arXiv:1501.00155.Google Scholar
Yang, F. & Väänänen, J. (2016). Propositional logics of dependence. Annals of Pure and Applied Logic, 167(7), 557–589.CrossRefGoogle Scholar