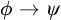CRAIG INTERPOLATION THEOREM FAILS IN BI-INTUITIONISTIC PREDICATE LOGIC

Abstract

In this article we show that bi-intuitionistic predicate logic lacks the Craig Interpolation Property. We proceed by adapting the counterexample given by Mints, Olkhovikov and Urquhart for intuitionistic predicate logic with constant domains [13]. More precisely, we show that there is a valid implication $\phi \rightarrow \psi $ with no interpolant. Importantly, this result does not contradict the unfortunately named ‘Craig interpolation’ theorem established by Rauszer in [24] since that article is about the property more correctly named ‘deductive interpolation’ (see Galatos, Jipsen, Kowalski and Ono’s use of this term in [5]) for global consequence. Given that the deduction theorem fails for bi-intuitionistic logic with global consequence, the two formulations of the property are not equivalent.

1 Introduction

Bi-intuitionistic logic (or Heyting–Brouwer logic) comes rather naturally from adding the algebraic dual of the intuitionistic implication $\rightarrow $ to the language of intuitionistic logic. This connective is known as ‘co-implication’, and we denote it in what follows by ‘ ’. ¹ In the 1970s, Rauszer started an intense study of various technical aspects of both propositional and predicate bi-intuitionistic logic in a series of interesting articles spanning over a decade [18–23]. This work has been picked up in recent years by a number of scholars [1–4, 6, 7, 9, 13, 17, 26, 27] and results on all sorts of proof-theoretic and model-theoretic properties of these systems have been produced.

In this paper we are concerned with refuting the Craig Interpolation Property for predicate bi-intuitionistic logic. In other words, we will show that there are valid implications $\phi \rightarrow \psi $ with no interpolant in the sense of a formula $\theta $ in the intersection of the vocabularies of $\phi $ and $\psi $ such that both $\phi \rightarrow \theta $ and $\theta \rightarrow \psi $ are valid. Our counterexample is extracted from [12] where the Craig interpolation problem for predicate intuitionistic logic with constant domains is solved negatively. More specifically, we consider the implication $\phi \rightarrow \psi $ where

$$ \begin{align*}\phi:= \forall x\exists y(P(y) \wedge (Q(y) \to R(x))) \wedge \neg\forall xR(x), \end{align*} $$

and

$$ \begin{align*}\psi:= \forall x(P(x) \to (Q(x) \vee S)) \to S. \end{align*} $$

One of the reasons why our construction works is because bi-intuitionistic predicate logic is well-known to be sound with respect to its constant domain semantics [21]. Hence, the effect of adding the co-implication connective is that one can restrict attention to Kripke models with constant domains (this has led some authors to question the status of as an intuitionistic connective [11]).

Rauszer had already studied the interpolation problem for both predicate and propositional versions of bi-intuitionistic logic for global consequence (which we will denote by $\models ^g$ ) in [23]. ² However, she had only established interpolation in a much weaker version properly known as ‘deductive interpolation’ (see [5]): if $\phi \vDash ^g \psi $ there is a formula $\theta $ in the intersection of the vocabularies of $\phi $ and $\psi $ such that both $\phi \vDash ^g \theta $ and $\theta \vDash ^g \psi $ . Given that in bi-intuitionistic logic the deduction theorem fails for global consequence, ³ deductive interpolation is not equivalent to the usual Craig interpolation. Craig interpolation for propositional bi-intuitionistic logic was established only recently by a complex proof-theoretic argument [9]. Unfortunately, as we will see, those techniques cannot be extended to the predicate case.

López-Escobar had observed in [11] that bi-intuitionistic predicate logic is not conservative as an extension of intuitionistic predicate logic simply because the axiom of constant domains is derivable in the former. It is known, however, that bi-intuitionistic predicate logic is a conservative extension of constant domain intuitionistic predicate logic [3]. Then, one could wonder whether this trivialises the result in the present paper given the argument refuting interpolation for the latter in [12]. A minute of reflection suffices to show the reader that this is not so, for the argument in [12] only establishes that the interpolant does not exist in the language of predicate intuitionistic logic which does not include the new co-implication connective. It does, on the other hand, indicate that the present result is quite natural.

Recently [25], a number of questions have arisen as to the correctness of Rauszer’s completeness theorem for predicate bi-intuitionistic logic with respect to the Kripke semantics of constant domains. Three fundamental flaws of Rauszer’s proofs are outlined in [25]: (i) the fact that they mistakenly mix up properties of global and local consequence relations, (ii) the contradictory choice of rooted frames in the completeness proof which would validate non-theorems of bi-intuitionistic logic, and (iii) an incorrect application of some results by Gabbay. Incidentally, there is an alternative completeness argument by Klemke in [8], where bi-intuitionistic predicate logic is studied possibly for the first time in print (and, as far as we know, independently from Rauszer’s work) and that contains other errors. This paper appears to have been sadly neglected in the history of the subject and it contains valuable techniques such as a version of the unraveling construction used in [13] (see [8, Definition 4.1]).

Let us note, however, that the central result in the present paper does not actually require any appeal to completeness. All we need is (i) that the axiom of constant domains is a theorem of bi-intuitionistic predicate logic and (ii) that bi-intuitionistic predicate logic is sound with respect to the Kripke semantics for intuitionistic logic of constant domains. This is because our implication $\phi \rightarrow \psi $ described above is a theorem of intuitionistic predicate logic with the addition of the axiom of constant domains, and hence by (i), a theorem of bi-intuitionistic predicate logic. Furthermore, if there would be a proof-theoretic Craig interpolant for this implication, then, by (ii), it would be a semantic interpolant and hence we would get the desired contradiction reasoning as in Theorem 2.

The article is arranged as follows: in $\S $ 2 we introduce all the required technical preliminaries that we will use in the construction of our counterexample, namely the language of the logic and its models, as well as the notion of a bi-asimulation (among a few other things); in $\S $ 3 we introduce the Craig Interpolation Property, Mints’s counterexample from [12] and we show how to adapt the technical argument in that paper to obtain the central result of the present article (Theorem 2); finally, in $\S $ 4 we provide some concluding remarks on the failure of interpolation described here.

2 Preliminaries and notation

2.1 The first-order language

In this paper we will use ‘first-order’ and ‘predicate’ interchangeably as qualifiers for a logic. We start by fixing some general notational conventions. In this paper, we identify the natural numbers with finite ordinals. We denote by $\omega $ the smallest infinite ordinal, and by $\mathbb {N}$ the set $\omega \setminus \{0\}$ . For any $n \in \omega $ , we will denote by $\bar {o}_n$ the sequence $(o_1,\ldots , o_n)$ of objects of any kind; moreover, somewhat abusing the notation, we will denote $\{o_1,\ldots , o_n\}$ by $\{\bar {o}_n\}$ . The ordered $1$ -tuple will be identified with its only member. For any given $m,n \in \omega $ , the notation $(\bar {p}_m)^\frown (\bar {q}_n)$ denotes the concatenation of $\bar {p}_m$ and $\bar {q}_n$ , and the notation $\bar {p}_n\mapsto \bar {q}_n$ denotes the relation $\{(p_i, q_i)\mid 1 \leq i \leq n\}$ ; the latter relation is often explicitly assumed to define a function.

More generally, if f is any function, then we will denote by $dom(f)$ its domain and by $rang(f)$ the image of $dom(f)$ under f; if $rang(f) \subseteq M$ , we will also write $f: dom(f) \to M$ . If $f: X \to Y$ is any function, and Z is any set, then we denote by $[f]Z$ the set $\{q \in Y\mid (\exists p \in Z)(f(p) = q)\}$ ; in particular, if $\bar {p}_n\mapsto \bar {q}_n$ defines a function, then $[\bar {p}_n\mapsto \bar {q}_n]Z$ stands for $\{q_i\mid p_i \in Z,\,1 \leq i \leq n\}$ .

For a given set $\Omega $ and a $k\in \omega $ , the notation $\Omega ^k$ (resp. $\Omega ^{\neq k}$ ) will denote the k-th Cartesian power of $\Omega $ (resp. the set of all k-tuples from $\Omega ^k$ such that their elements are pairwise distinct). We remind the reader that in the special case when $k = 0$ it is usual to define $\Omega ^0:= \{\emptyset \} = 1$ , given our earlier convention about the natural numbers. Moreover we will denote the powerset of $\Omega $ by $\mathscr {P}(\Omega )$ . We also define that $\Omega ^\ast := \bigcup _{n \geq 0}\Omega ^n$ . Finally, the notation $\lvert X\rvert $ will denote the cardinality of the set X, so that, for example, $\lvert X\rvert = \omega $ will mean that X is countably infinite.

In this paper, we consider a first-order language without equality based on any set of predicate letters (including $0$ -ary predicates, that is to say, propositional letters) and individual constants. We do not allow functions, though.

An ordered couple of sets $\Sigma = (Pred_\Sigma , Const_\Sigma )$ comprising all the predicate letters and constants allowed in a given version of the first-order language will be called the signature of this language. Signatures will be denoted by letters $\Sigma $ and $\Theta $ . For a given signature $\Sigma $ , the elements of $Pred_\Sigma $ will be denoted by $P^n$ and $Q^n$ , where $n> 0$ indicates the arity, and the elements of $Const_\Sigma $ will be denoted by lowercase Latin letters like a, b, c, d and so on. All these notations and all of the other notations introduced in this section can be decorated by all sorts of sub- and superscripts. We will often use the notation $\Sigma _n$ for the set of n-ary predicates in a given signature $\Sigma $ . Our signature will not contain function symbols as they are not necessary for the counterexample, and clearly our counterexample in a poorer signature carries over to more complex ones.

Even though we have defined signatures as ordered pairs, we will somewhat abuse the notation in the interest of suggestivity and, given a set $\Pi $ of predicates and a set $\Delta $ of individual constants outside a given signature $\Sigma $ , we will denote by $\Sigma \cup \Pi \cup \Delta $ the signature where the predicates from $\Pi $ are added to $Pred_\Sigma $ with their respective arities and the constants from $\Delta $ are added to $Const_\Sigma $ . Moreover, we will write $\Sigma \subseteq \Theta $ iff there exists a set $\Pi $ of predicates and a set $\Delta $ of individual constants outside $\Sigma $ such that $\Theta = \Sigma \cup \Pi \cup \Delta $ ; in other words, iff $\Theta $ extends $\Sigma $ as a signature. In case $\Pi = Pred_{\Sigma '}$ and $\Delta = Const_{\Sigma '}$ , we also express this same fact by writing $\Theta = \Sigma \cup \Sigma '$ ; furthermore, in case we have $P \in \Pi $ and $c \in \Delta $ , we will write $P \notin \Sigma $ and $c \notin \Sigma $ . Similarly, if $\Theta _1 = \Sigma \cup \Pi _1 \cup \Delta _1$ and $\Theta _2 = \Sigma \cup \Pi _2 \cup \Delta _2$ , for pairwise non-overlapping sets of predicates $\Pi _1$ and $\Pi _2$ and sets of constants $\Delta _1$ and $\Delta _2$ , we will write that $\Sigma = \Theta _1 \cap \Theta _2$ .

If $\Sigma $ is a signature, then the set of first-order formulas is generated from $\Sigma $ in the usual way, using the set of logical symbols (here stands for the bi-intuitionistic co-implication) and the set of (individual) variables $Var := \{ v_i \mid i < \omega \}$ , and will be denoted by $L(\Sigma )$ . The elements of $Var$ will be also denoted by $x,y,z, w$ , and the elements of $L(\Sigma )$ by Greek letters like $\phi $ , $\psi $ and $\theta $ . As is usual, we will use $\neg \phi $ as an abbreviation for $\phi \to \bot $ .

For any given signature $\Sigma $ , and any given $\phi \in L(\Sigma )$ , we define $FV(\phi )$ and $BV(\phi )$ , its sets of free and bound variables, by the usual inductions. These sets are always finite. We will denote the set of $L(\Sigma )$ -formulas with free variables among the elements of $\bar {x}_n \in Var^{\neq n}$ by $L_{\bar {x}_n}(\Sigma )$ ; in particular, $L_\emptyset (\Sigma )$ will stand for the set of $\Sigma $ -sentences. If $\varphi \in L_{\bar {x}_n}(\Sigma )$ (resp. $\Gamma \subseteq L_{\bar {x}_n}(\Sigma )$ ), then we will also express this by writing $\varphi (\bar {x}_n)$ (resp. $\Gamma (\bar {x}_n)$ ).

Similarly, given a $\phi \in L(\Sigma )$ , one can define a signature $\Theta _\phi $ such that, for any signature $\Sigma '$ we have $\phi \in L(\Sigma ')$ iff $\Theta _\phi \subseteq \Sigma '$ . The definition proceeds by induction on the construction of $\phi $ and looks as follows:

• • $\Theta _{P(\bar {t}_n)} = (\{P^n\}, \{\bar {t}_n\}\cap Const_\Sigma )$ , for any $P \in \Sigma _n$ and $\bar {t}_n \in (Var \cup Const_\Sigma )^n$ .

• • $\Theta _\bot = \Theta _\top = \emptyset $ .

• • $\Theta _{\psi \circ \theta } = \Theta _{\psi }\cup \Theta _{\theta }$ for .

• • $\Theta _{\circ \psi } = \Theta _{\psi }$ for $\circ \in \{\forall x, \exists x\mid x \in Var\}$ .

If $X \subseteq Var$ is finite and $f: X \to Const_\Sigma $ , then, for any $\phi \in L(\Sigma )$ , we denote by $\phi [f] \in L(\Sigma )$ the result of simultaneously replacing every free occurrence of every $x \in X$ by $f(x)$ . The precise definition of this operation proceeds by induction on the construction of $\varphi \in L(\Sigma )$ and runs as follows:

• • $P(\bar {t}_n) := P(\bar {s}_n)$ , where $P \in \Sigma _n$ , and $\bar {t}_n, \bar {s}_n \in (Var \cup Const_\Sigma )^n$ are such that, for all $1 \leq i \leq n$ we have:

  $$ \begin{align*} s_i := \begin{cases} f(t_i),\text{ if }t_i \in X,\\ t_i,\text{ otherwise.} \end{cases} \end{align*} $$

• • $(\phi )[f] : = \phi $ for $\phi \in \{\bot , \top \}$ .

• • $(\phi \circ \psi )[f] : = \phi [f]\circ \psi [f]$ , for .

• • $(Qx\phi )[f] : = Qx(\phi [f\upharpoonright (X \setminus \{x\})])$ , for $x \in Var$ and $Q \in \{\forall , \exists \}$ .

Since $dom(f)$ is always finite, we will write $\phi [c_1/x_1,\ldots ,c_n/x_n]$ (or, alternatively, $\phi [\bar {c}_n/\bar {x}_n]$ ) in place of $\varphi [f]$ , whenever f is $\bar {x}_n \mapsto \bar {c}_n$ . It is clear that every $\varphi [f]$ can be written in this format. An important particular case is when $dom(f) = \{x\}$ , so that we can write $\phi [f]$ as $\phi [c/x]$ for the corresponding $c \in Const_\Sigma $ .

The following lemma states that our substitution operations work as expected. We omit the straightforward but tedious inductive proof.

Lemma 1. Let $\Sigma $ be a signature, let $\bar {x}_n \in Var^{\neq n}$ , $\phi \in L_{\bar {x}_n}(\Sigma )$ , $\bar {y}_m \in Var^{\neq m}$ , and $\bar {z}_k \in Var^{\neq k}$ be such that $\{\bar {z}_k\} = \{\bar {x}_n\}\setminus \{\bar {y}_m\}$ . Moreover, let $\bar {c}_m \in (Const_\Sigma )^m$ , and let $(i_1,\ldots ,i_m)$ be a permutation of $(1,\ldots , m)$ . Then the following statements hold:

1. 1. $\phi [\bar {c}_m/\bar {y}_m] \in L_{\bar {z}_k}(\Sigma )$ .

2. 2. $\phi [\bar {c}_m/\bar {y}_m] = \phi [c_{i_1}/y_{i_1},\ldots , c_{i_m}/y_{i_m}]$ .

3. 3. $\phi [\bar {c}_m/\bar {y}_m] = \phi [c_{1}/y_{1}]\ldots [c_{m}/y_{m}]$ .

4. 4. If $FV(\phi ) \cap \{\bar {x}_n\} = \{x_{j_1},\ldots ,x_{j_m}\}$ , then $\phi [\bar {c}_n/\bar {x}_n] = \phi [c_{j_1}/x_{j_1},\ldots ,c_{j_m}/x_{j_m}]$ .

5. 5. If $\psi \in L_{\bar {x}_n}(\Sigma \cup \{\bar {c}_m\})$ , and $\{\bar {y}_m\} \cap (\{\bar {x}_n\} \cup BV(\psi )) = \emptyset $ , then there exists a $\chi \in L_{(\bar {x}_n)^\frown (\bar {y}_m)}(\Sigma )$ such that $\chi [\bar {c}_m/\bar {y}_m] = \psi $ .

6. 6. $\Theta _{\phi [\bar {c}_m/\bar {y}_m]} \subseteq \Theta _\phi \cup \{\bar {c}_m\}$ .

Note that Part 2 of the lemma holds just by the notational convention, since permutations of the set of the ordered pairs define one and the same function. Moreover, the joint effect of Parts 2 and 3 is that one can break up $[\bar {c}_n/\bar {x}_n]$ into a finite set of parts of arbitrary size and then apply those parts to a given $\phi $ in arbitrary order without affecting the result of a substitution. The latter is something that does not hold for the substitutions of arbitrary terms but is valid in our case due to the restriction to constants.

The notion of substitution is necessary for a correct inductive definition of a sentence that is independent from the inductive definition of an arbitrary formula. More precisely, let $\Sigma $ be a signature and let c be any constant, perhaps outside $\Sigma $ . Then $L_\emptyset (\Sigma )$ is the smallest subset $Sent(\Sigma )$ of $L(\Sigma )$ satisfying the following conditions:

• • $P(\bar {c}_n), \bot , \top \in Sent(\Sigma )$ for all $n \geq 1$ , $P \in \Sigma _n$ , and $\bar {c}_n \in (Const_\Sigma )^n$ .

• • If $\phi , \psi \in Sent(\Sigma )$ , then $(\phi \circ \psi ) \in Sent(\Sigma )$ for all .

• • If $x \in Var$ and $\phi [c/x] \in Sent(\Sigma \cup \{c\})$ , then $\forall x\phi , \exists x\phi \in Sent(\Sigma )$ .

2.2 Semantics

For any given signature $\Sigma $ , a constant domain intuitionistic Kripke $\Sigma $ -model is a structure of the form $\mathcal {M} = (W, \prec , D, V, I)$ such that:

• • W is a non-empty set of worlds, or nodes.

• • The accessibility relation $\prec \subseteq W \times W$ is reflexive and transitive (i.e., a pre-order).

• • D is a non-empty set (or domain) of objects which is disjoint from W.

• • The mapping V is a function from $Pred_\Sigma \times W$ into the set $\bigcup _{n \geq 0}\mathscr {P}(D^n)$ such that, for every $n \geq 0$ , every $P \in \Sigma _n$ , and all $w, v \in W$ , it is true that $V(P, w) \subseteq D^n$ and

  $$ \begin{align*} w \prec v \Rightarrow V(P, w) \subseteq V(P, v). \end{align*} $$

  Given a $P \in \Sigma _n$ , we will sometimes consider the unary projection functions of the form $V_P:W \to \mathscr {P}(D^n)$ arising from the binary function V. It is clear that we may view V as the union of the corresponding family of the unary functions, that is to say, that we can assume $V = \bigcup _{P \in Pred_\Sigma }V_P$ .

• • $I: Const_\Sigma \to D$ is the function interpreting the individual constants.

In what follows, we will always assume the particular case when I is just the identity function on $Const_\Sigma $ ; in other words, we will only consider the constants that are names of themselves.

An interesting particular case arises when $P \in \Sigma _0$ . In this case, our definition says that $V_P:W \to \mathscr {P}(D^0)$ , but $\mathscr {P}(D^0) = \mathscr {P}(\{\emptyset \}) = \{\emptyset , \{\emptyset \}\} = \{0,1\} = 2$ , given our identification of natural numbers with the finite ordinals. Therefore, $V_{P}$ in this case is, in effect, a function from W to $\{0, 1\}$ , and $V_{P}$ returns $1$ for a given w iff $P^0$ holds at w in $\mathcal {M}$ .

Since we will only consider in this paper the models of the type described above, we will simply call them $\Sigma $ -models.

When we use subscripts and other decorated model notations, we strive for consistency in this respect. Some examples of this notational principle are given below:

$$ \begin{align*}\mathcal{M} = (W, \prec, D, V, I),\, \mathcal{M}' = (W', \prec', D', V', I'),\, \mathcal{M}_n = (W_n, \prec_n, D_n, V_n, I_n). \end{align*} $$

As is usual, we denote the reduct of a $\Sigma $ -model $\mathcal {M}$ to a signature $\Theta \subseteq \Sigma $ by $\mathcal {M}\upharpoonright \Theta $ .

As for the reverse operation of expanding a model of a smaller signature to a model of a larger signature, if $\mathcal {M}$ is a $\Sigma $ -model, $P^{n_1}_1, \ldots , P^{n_k}_k \notin \Sigma $ are pairwise distinct, and $\mathbf {A} \subseteq D$ , then, for any given sequence of $\pi _1:W\to \mathscr {P}(D^{n_1}), \ldots , \pi _k:W\to \mathscr {P}(D^{n_k})$ of functions monotonic relative to $\prec $ , we will denote by $(\mathcal {M}; \bar {P}_k\mapsto \bar {\pi }_k; \mathbf {A})$ the unique $\Sigma \cup \{ P^{n_1}_1, \ldots ,P^{n_k}_k\}\cup \mathbf {A}$ -model $\mathcal {M}'$ such that $\mathcal {M}'\upharpoonright \Sigma = \mathcal {M}$ , $V'(P^{n_i}_i, w) = \pi _i(w)$ for all $w \in W$ , and $I'(a) = a$ for all $1 \leq i \leq k$ and all $a \in \mathbf {A}$ . In case $k = 0$ or $\mathbf {A} = \emptyset $ , we will write $(\mathcal {M};\mathbf {A})$ or $(\mathcal {M}; \bar {P}_k\mapsto \bar {\pi }_k)$ , respectively.

The semantics is given by the following forcing relation defined by induction on the construction of a sentence. If $\Sigma $ is a signature, $\mathcal {M}$ is a $\Sigma $ -model, $w \in W$ , and $\phi \in L_\emptyset (\Sigma \cup D)$ , then we write that $(\mathcal {M}; D), w \models \phi $ and say that $\phi $ is true at w in $(\mathcal {M}; D)$ iff it follows from the following clauses:

In the clauses given above, as well as in the similar places below, like Lemma 2 and Definition 4, we also use the symbols $\forall $ and $\exists $ in the defining part to denote the (classical) quantifiers in the meta-language. We are certain that this creates no ambiguities.

Note that the assumption of constant domains allows for a simplification of the clause treating the universal quantifier. The following lemma then spells out the consequences of our definition for the defined connective $\neg $ .

Lemma 2. If $\Sigma $ is a signature, $\mathcal {M}$ is a $\Sigma $ -model, $w \in W$ , and $\phi \in L_\emptyset (\Sigma \cup D)$ then we have

$$ \begin{align*} (\mathcal{M}; D), w\models \neg\phi &\Leftrightarrow (\forall v\succ w)((\mathcal{M}; D), v\not\models \phi). \end{align*} $$

The proof is immediate by the definition and is omitted.

We then extend this semantics to arbitrary models by setting that for a $\Sigma $ -model $\mathcal {M}$ , and for a $\phi \in L_\emptyset (\Sigma )$ , we have $\mathcal {M}, w\models \phi $ iff $(\mathcal {M};D), w\models \phi $ . The following theorem is then immediate.

Theorem 1. Let $\Sigma , \Theta $ be signatures such that $\Sigma \subseteq \Theta $ , let $\mathcal {M}$ be a $\Theta $ -model, let $w \in W$ , and let $\phi \in L_\emptyset (\Sigma )$ . Then $\mathcal {M}, w \models \phi $ iff $\mathcal {M}\upharpoonright \Sigma , w \models \phi $ .

Theorem 1 is often referred to as Expansion Property in the literature on abstract model theory.

Next, we adopt the standard definitions of validity, satisfiability and of semantic consequence relation. In particular, given a signature $\Sigma $ , a $\Gamma \cup \{\phi \} \subseteq L_\emptyset (\Sigma )$ , a $\Sigma $ -model $\mathcal {M}$ , and a $w \in W$ , we say that $(\mathcal {M}, w)$ satisfies $\Gamma $ , and write $\mathcal {M}, w\models \Gamma $ iff we have $\mathcal {M}, w\models \psi $ for all $\psi \in \Gamma $ . Furthermore, we say that $\phi $ is a consequence of $\Gamma $ and write $\Gamma \models \phi $ iff for every $\Sigma $ -model $\mathcal {M}$ , and every $w \in W$ , $\mathcal {M}, w\models \Gamma $ implies that $\mathcal {M}, w\models \phi $ . In case $\Gamma = \{\psi \}$ for some $\psi \in L_\emptyset (\Sigma )$ , we will omit the brackets and simply write $\psi \models \phi $ , and in case $\Gamma = \emptyset $ we will write $\models \phi $ omitting $\Gamma $ altogether.

Having now both the language and its semantic apparatus in place, we can speak of the logical system $\mathsf {FOBIL}$ of bi-intuitionistic predicate logic. As a model-theoretic language, $\mathsf {FOBIL}$ can be presented as a fragment of classical first-order logic $\mathsf {FOCL}$ by means of an appropriate standard translation along the lines of [15]. On the other hand, $\mathsf {FOBIL}$ can be seen as resulting from intuitionistic predicate logic $\mathsf {FOIL}$ by first restricting its semantics to the constant-domain Kripke models and then adding as the new connective to the language. An even closer relation exists between $\mathsf {FOBIL}$ and the intuitionistic logic of constant domains $\mathsf {CD}$ which can be viewed as the -free fragment of $\mathsf {FOBIL}$ .

2.3 Bi-asimulations

An important semantic concept related to bi-intuitionistic predicate logic is the notion of first-order bi-asimulation. This notion can be defined as follows.

Definition 1. Let $\Sigma $ be a signature, and let $\mathcal {M}_0$ , $\mathcal {M}_1$ be $\Sigma $ -models. A non-empty relation A is called a first-order bi-asimulation iff the following conditions are satisfied for all $i,j$ such that $\{i,j\} = \{0,1\}$ , and for all $n \in \omega $ , all $P \in \Sigma _m$ , all (maybe non-distinct) $j_1, \ldots , j_m \leq n$ , all $(w)^\frown (\bar {a}_n) \in W_i\times (D_i)^n$ and all $(v)^\frown (\bar {b}_n) \in W_j\times (D_j)^n$ such that $(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$ :

(type) $$ \begin{align} &A \subseteq \bigcup_{n \in \omega}((W_0\times (D_0)^n) \times (W_1\times (D_1)^n) )\cup ((W_1\times (D_1)^n) \times (W_0\times (D_0)^n) ), \end{align} $$

(atom) $$ \begin{align} &(\mathcal{M}_i; D_i), w\models P(a_{j_1},\ldots,a_{j_m}) \Rightarrow (\mathcal{M}_j; D_j), v\models P(b_{j_1},\ldots,b_{j_m}), \end{align} $$

(back) $$ \begin{align} &(\mathsf{\forall} v_0 \succ_j v)(\exists w_0\succ_i w)((w_0)^\frown(\bar{a}_n)\mathrel{A}(v_0)^\frown(\bar{b}_n)\,\&\,(v_0)^\frown(\bar{b}_n)\mathrel{A}(w_0)^\frown(\bar{a}_n)), \end{align} $$

(forth) $$ \begin{align} &(\forall w_0 \prec_i w)(\exists v_0\prec_j v)((w_0)^\frown(\bar{a}_n)\mathrel{A}(v_0)^\frown(\bar{b}_n)\,\&\,(v_0)^\frown(\bar{b}_n)\mathrel{A}(w_0)^\frown(\bar{a}_n)), \end{align} $$

(left) $$ \begin{align} &(\forall b \in D_j)(\exists a\in D_i)((w)^\frown(\bar{a}_n)^\frown(a)\mathrel{A}(v)^\frown(\bar{b}_n)^\frown(b)), \end{align} $$

(right) $$ \begin{align} &(\forall a \in D_i)(\exists b\in D_j)((w)^\frown(\bar{a}_n)^\frown(a)\mathrel{A}(v)^\frown(\bar{b}_n)^\frown(b)). \end{align} $$

In the case where we have $(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$ in the assumptions of Definition 1, we will say that the first-order bi-asimulation A is from $(w)^\frown (\bar {a}_n)$ to $(v)^\frown (\bar {b}_n)$ . Since we are not going to discuss any other kinds of bi-asimulation relations in this paper, we will omit in what follows the qualification ‘first-order’ and will simply speak of bi-asimulations. The following lemma shows that first-order bi-intuitionistic formulas are preserved under bi-asimulations.

Lemma 3. Let $\Sigma $ be a signature, let $\mathcal {M}_0$ , $\mathcal {M}_1$ be $\Sigma $ -models, let $n \in \omega $ , let $i,j$ be such that $\{i,j\} = \{0,1\}$ , let $(w)^\frown (\bar {a}_n) \in W_i\times (D_i)^n$ and $(v)^\frown (\bar {b}_n) \in W_j\times (D_j)^n$ , and let A be a bi-asimulation between $\mathcal {M}_0$ and $\mathcal {M}_1$ such that $(w)^\frown (\bar {a}_n)\mathrel {A}(v)^\frown (\bar {b}_n)$ . Then for every tuple $\bar {x}_n \in Var^{\neq n}$ and every $\phi \in L_{\bar {x}_n}(\Sigma )$ it is true that

$$ \begin{align*} (\mathcal{M}_i; D_i), w\models \phi[\bar{a}_n/\bar{x}_n] \Rightarrow (\mathcal{M}_j; D_j), v\models \phi[\bar{b}_n/\bar{x}_n]. \end{align*} $$

Proof. By induction on the construction of $\phi $ .

Induction basis. If $\phi = P(x_{j_1},\ldots ,x_{j_m})$ for some (maybe non-distinct) $j_1, \ldots , j_m \leq n$ and some $P \in \Sigma _m$ , then the statement of the Lemma follows from condition (atom) of Definition 1 and the fact that we have $\phi [\bar {a}_n/\bar {x}_n] = P(a_{j_1},\ldots ,a_{j_m})$ and $\phi [\bar {b}_n/\bar {x}_n] = P(b_{j_1},\ldots ,b_{j_m})$ .

Induction step. The cases when $\phi = \psi \wedge \theta $ and when $\phi = \psi \vee \theta $ are straightforward. We consider the remaining cases:

Case 1. $\phi = \psi \to \theta $ . If $(\mathcal {M}_j; D_j), v\not \models (\psi \to \theta )[\bar {b}_n/\bar {x}_n]$ , then $(\mathcal {M}_j; D_j), v\not \models \psi [\bar {b}_n/\bar {x}_n] \to \theta [\bar {b}_n/\bar {x}_n]$ , and hence there exists a $v_0 \mathrel {\succ _j}v$ such that both $(\mathcal {M}_j; D_j), v_0\models \psi [\bar {b}_n/\bar {x}_n]$ and $(\mathcal {M}_j; D_j), v_0\not \models \theta [\bar {b}_n/\bar {x}_n]$ . But then, by condition (back), there must be a $w_0 \mathrel {\succ _i}w$ such that both $(w_0)^\frown (\bar {a}_n)\mathrel {A}(v_0)^\frown (\bar {b}_n)$ and $(v_0)^\frown (\bar {b}_n)\mathrel {A}(w_0)^\frown (\bar {a}_n)$ . Now the Induction Hypothesis implies that both $(\mathcal {M}_i; D_i), w_0\models \psi [\bar {a}_n/\bar {x}_n]$ and $(\mathcal {M}_i; D_i), w_0\not \models \theta [\bar {a}_n/\bar {x}_n]$ . Thus we get that

$$ \begin{align*} (\mathcal{M}_i; D_i), w\not\models (\psi[\bar{a}_n/\bar{x}_n] \to \theta[\bar{a}_n/\bar{x}_n]) = (\psi \to \theta)[\bar{a}_n/\bar{x}_n]. \end{align*} $$

Case 2. . The case is dual to Case 1.

Case 3. $\phi = \forall x\psi $ . Then we might have $x \in \{\bar {x}_n\}$ , but we can always avoid this inconvenience by choosing an $m \geq 0$ , and some pairwise distinct $j_1,\ldots , j_m \leq n$ such that $\{x_{j_1},\ldots ,x_{j_m}\} = FV(\forall x\phi )\cap \{\bar {x}_n\}$ . For this m-tuple, we will have, $x \notin \{x_{j_1},\ldots ,x_{j_m}\}$ , and Lemma 1.4 implies that

$$ \begin{align*} (\forall x\psi)[\bar{b}_n/\bar{x}_n] = (\forall x\psi)[b_{j_1}/x_{j_1},\ldots,b_{j_m}/x_{j_m}] = \forall x(\psi[b_{j_1}/x_{j_1},\ldots,b_{j_m}/x_{j_m}]). \end{align*} $$

But then we reason as follows. If $(\mathcal {M}_j; D_j), v\not \models (\forall x\psi )[\bar {b}_n/\bar {x}_n] = \forall x(\psi [b_{j_1}/x_{j_1},\ldots , b_{j_m}/x_{j_m}])$ , then we must have $(\mathcal {M}_j; D_j), v\not \models \psi [b_{j_1}/x_{j_1},\ldots ,b_{j_m}/x_{j_m}][b/x]$ for some $b \in D_j$ , and hence $(\mathcal {M}_j; D_j), v\not \models \psi [b_{j_1}/x_{j_1},\ldots ,b_{j_m}/x_{j_m}, b/x]$ by Lemma 1. Moreover, condition (left) of Definition 1 implies that, for some $a \in D_i$ we must have $(w)^\frown (\bar {a}_n)^\frown (a)\mathrel {A}(v)^\frown (\bar {b}_n)^\frown (b)$ . Since also $FV(\psi )\subseteq \{x_{j_1},\ldots ,x_{j_m}\} \cup \{x\}$ , the Induction Hypothesis is applicable and yields that $(\mathcal {M}_i; D_i), w\not \models \psi [a_{j_1}/x_{j_1},\ldots ,a_{j_m}/x_{j_m}, a/x]$ , whence, further, that $(\mathcal {M}_i; D_i), w\not \models \psi [a_{j_1}/x_{j_1},\ldots , a_{j_m}/x_{j_m}][a/x]$ by Lemma 1.

But then it follows (again applying Lemma 1.4) that

$$ \begin{align*} (\mathcal{M}_i; D_i), w\not\models \forall x(\psi[a_{j_1}/x_{j_1},\ldots,a_{j_m}/x_{j_m}]) = (\forall x\psi)[\bar{a}_n/\bar{x}_n]. \end{align*} $$

Case 4. $\phi = \exists x\psi $ . The case is dual to Case 3.

Remark 1. Asimulations had been initially introduced by the first author in studying the expressive power of intuitionistic propositional logic in [14], and they turned out to be equivalent to the intuitionistic bisimulations of [10]. In [15], they were adapted to $\mathsf {FOIL}$ , and only a small step was then required to further adapt them to $\mathsf {CD}$ ; this step was done in [12, Definition 6.1] which only differs from Definition 4 in that the condition (forth) is absent. The latter condition first appeared in [1].

Due to the absence of the Boolean, or classical, negation in intuitionistic and bi-intuitionistic logic, the (bi-)asimulations capture an inclusion of theories at the nodes of Kripke models that they connect to one another, rather than the coincidence of such theories. This asymmetry makes it necessary to define (bi-)asimulations as subsets of $\bigcup _{n \in \omega }((W_0\times (D_0)^n) \times (W_1\times (D_1)^n) )\cup ((W_1\times (D_1)^n) \times (W_0\times (D_0)^n) )$ rather than subsets of $\bigcup _{n \in \omega }(W_0\times (D_0)^n) \times (W_1\times (D_1)^n)$ ; another option, taken up in [1, 10], would be to define (bi-)asimulations as pairs of binary relations, where one relation is a subset of $\bigcup _{n \in \omega }(W_0\times (D_0)^n) \times (W_1\times (D_1)^n)$ and the other one a subset of $\bigcup _{n \in \omega }(W_1\times (D_1)^n) \times (W_0\times (D_0)^n)$ . The asymmetric nature of (bi)-asimulations also shows itself in the fact that condition (atom) can only be given in the form of an implication and not as a bi-conditional.

A more detailed discussion of the intuitions behind different conditions in the asimulation definition can be found in several published articles; we especially recommend [14, pp. 350–351] and [15, p. 812]. Although the explanations there are given relative to the intuitionistic logic, all of them are also applicable to the bi-intuitionistic case. A more general and systematic inquiry into the dependence between the expressive power of a logic and a form of its characteristic simulation relation can be found in [16], where the first author basically shows, among other things, that, in the presence of classical $\vee $ and $\wedge $ in the language, the symmetry of a characteristic simulation is equivalent to a presence of a connective expressing non-constant and non-monotone Boolean function.

Since we are not treating the general theory of bi-asimulations in this paper, but are using them instead, as a technical tool, we omit any further details.

Remark 2. It is rather straightforward to show, by combining the arguments given in [1, 15], that the invariance under bi-asimulations given in Definition 1 defines, for any given signature $\Sigma $ , the set of natural standard translations of first-order bi-intuitionistic formulas into classical first-order logic. Such a proof, however, is beyond the scope of the present paper.

3 Interpolation fails in the bi-intuitionistic setting

3.1 Craig Interpolation Property and Mints’s Counterexample

The Craig Interpolation Property, which was initially defined for $\mathsf {FOCL}$ , can be considered for $\mathsf {FOBIL}$ without any changes in the original definition. Therefore, we will say that $\mathsf {FOBIL}$ has Craig Interpolation Property (CIP) iff for any signature $\Sigma $ , and any $(\phi \to \psi ) \in L_\emptyset (\Sigma )$ such that $\models \phi \to \psi $ , there exists a $\theta \in L_\emptyset (\Theta _\phi \cap \Theta _\psi )$ such that both $\models \phi \to \theta $ and $\models \theta \to \psi $ . Any such $\theta $ is then called an interpolant for $\phi \to \psi $ .

Although CIP holds for both $\mathsf {FOCL}$ and $\mathsf {FOIL}$ , it is known to fail for $\mathsf {CD}$ . The counterexample to CIP for the latter logic was published in [12] and is obtained by setting

$$ \begin{align*}\phi:= \forall x\exists y(P(y) \wedge (Q(y) \to R(x))) \wedge \neg\forall xR(x), \end{align*} $$

and

$$ \begin{align*}\psi:= \forall x(P(x) \to (Q(x) \vee S)) \to S \end{align*} $$

in the definition for CIP given in the previous paragraph. Under these particular settings (fixed throughout the remaining part of this paper), we will call $\phi \to \psi $ Mints’s Counterexample to CIP. It was shown in [12] that $\phi \to \psi $ is valid in $\mathsf {CD}$ , but for no -free $\theta \in L_\emptyset (\Theta _\phi \cap \Theta _\psi ) = L_\emptyset (\{P^1, Q^1\})$ both $\phi \to \theta $ and $\theta \to \psi $ are valid in $\mathsf {CD}$ .

Since $\mathsf {CD}$ is exactly the -free fragment of $\mathsf {FOBIL}$ , the arguments of [12] also show that $\models \phi \to \psi $ . These arguments, however, are insufficient to show that $\phi \to \psi $ lacks an interpolant in $\mathsf {FOBIL}$ due to the richer language of the latter logic. The main purpose of the present paper is to close this gap and to show that Mints’s Counterexample works for $\mathsf {FOBIL}$ as well, and that therefore $\mathsf {FOBIL}$ lacks CIP. The next subsection contains a proof of these claims.

3.2 Refuting CIP

Our proof is an improvement on the proof given in [12]; it uses many of the same ideas albeit their application to this case requires several adjustments and a slight generalization.

We start by setting $\Sigma := \{P^1, Q^1\}$ . We will describe two particular $\Sigma $ -models and a bi-asimulation relation between them, and then we will show how to extend them to models satisfying $\phi $ and failing $\psi $ , respectively. The rest of the argument will then be exactly as in [12].

We start with the definitions of the building blocks for our models (repeating [12, Definition 7.1]).

Definition 2.

1. 1. A quasi-partition $(A,B,C)$ is defined by the following conditions:

   1. (a) $A \cup B \cup C = \mathbb {N}$ ;

   2. (b) $A,B,C$ are pairwise disjoint;

   3. (c) $\lvert A\rvert = \lvert C\rvert = \omega $ ;

   4. (d) $\lvert B\rvert \in \{\emptyset , \omega \}$ .

2. 2. A relation $\trianglelefteq $ on the set of all quasi-partitions is defined by

   $$\begin{align*}(A,B,C) \trianglelefteq (D,E,F) \Leftrightarrow [ A \subseteq D \wedge F \subseteq C]. \end{align*}$$

We immediately fix the following corollary to Definition 2.

Corollary 1. For any quasi-partitions $(A,B,C)$ and $(D,E,F)$ , if $(A,B,C) \trianglelefteq (D,E,F)$ , then $A \cup B \subseteq D \cup E$ .

Proof. If $(A,B,C) \trianglelefteq (D,E,F)$ , then $F \subseteq C$ ; in other words, $\mathbb {N}\setminus (D \cup E) \subseteq \mathbb {N}\setminus (A \cup B)$ . Therefore, by contraposition, $A \cup B \subseteq D \cup E$ .

We now fix two special quasi-partitions $\mathbf {v} = (\mathbf {v}_1, \mathbf {v}_2, \mathbf {v}_3) = ( 3 \mathbb {N}, 3 \mathbb {N} + 1, 3 \mathbb {N} + 2 )$ and $\mathbf {w} = (\mathbf {w}_1, \mathbf {w}_2, \mathbf {w}_3) = ( 2 \mathbb {N}, \emptyset , 2 \mathbb {N} + 1)$ . Our (fixed till the end of the present section) $\Sigma $ -models $\mathcal {M}_1$ and $\mathcal {M}_2$ are then as follows.

Definition 3. The structures $\mathcal {M}_1$ and $\mathcal {M}_2$ are such that:

1. 1. $W_1 = W_2 = W$ is the set of all quasi-partitions.

2. 2. $\prec _2 := \trianglelefteq $ , and, for all $(A,B,C), (D,E,F)\in W$ , we have $(A,B,C)\mathrel {\prec _1}(D,E,F)$ iff $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ and

   $$ \begin{align*} (\mathbf{v} \mathrel{\trianglelefteq} (A, B, C) \,\&\, \lvert B \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert E \cap \mathbf{v}_2\rvert = \omega. \end{align*} $$

3. 3. $D_1 = D_2 = \mathbb {N}$ .

4. 4. $V_i(P,(A,B,C)) = A \cup B$ , $V_i(Q,(A,B,C)) = A$ for all $(A,B,C) \in W$ , and $i \in \{1, 2\}$ .

5. 5. $I_1 = I_2 = \emptyset $ .

We now show that $\mathcal {M}_1$ , $\mathcal {M}_2$ are $\Sigma $ -models that can be extended to models verifying $\phi $ and falsifying $\psi $ , respectively.

Lemma 4. $\mathcal {M}_1$ and $\mathcal {M}_2$ are $\Sigma $ -models.

Proof. The extensions of Q are monotonic relative to $\trianglelefteq $ (hence also relative to $\prec _i$ for $i \in \{1,2\}$ ) by definition of $V_i$ . The extensions of P are monotonic relative to $\trianglelefteq $ (and thus also relative to $\prec _i$ for $i \in \{1,2\}$ ) by Corollary 1.

The relation $\prec _2 = \trianglelefteq $ is clearly a pre-order on W. We show that $\prec _1$ is a pre-order on the same set.

Reflexivity. Let $(A, B, C) \in W$ . We have $(A,B,C)\mathrel {\prec _1}(A,B,C)$ , since both $(A,B,C)\mathrel {\trianglelefteq }(A,B,C)$ and

$$ \begin{align*}(\mathbf{v} \trianglelefteq (A, B, C)\, \&\, \lvert B \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert B \cap \mathbf{v}_2\rvert = \omega \end{align*} $$

are trivially satisfied.

Transitivity. Let $(A, B, C), (D,E,F), (G,H,I) \in W$ be such that $(A,B,C)\mathrel {\prec _1}(D,E,F)$ and $(D,E,F)\mathrel {\prec _1}(G,H,I)$ . Then we must have both $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ and $(D,E,F)\mathrel {\trianglelefteq }(G,H,I)$ , and thus $(A,B,C)\mathrel {\trianglelefteq }(G,H,I)$ .

On the other hand, we must have both:

(1) $$ \begin{align} (\mathbf{v}\mathrel{\trianglelefteq} (A, B, C)\, \&\, \lvert B \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert E \cap \mathbf{v}_2\rvert = \omega \end{align} $$

and

(2) $$ \begin{align} (\mathbf{v} \mathrel{\trianglelefteq} (D,E,F)\, \&\, \lvert E \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert H \cap \mathbf{v}_2\rvert = \omega. \end{align} $$

But then we reason as follows:

(3) $$ \begin{align} & \mathbf{v} \mathrel{\trianglelefteq} (A, B, C) && \text{(premise)},\end{align} $$

(4) $$ \begin{align}&\lvert B \cap \mathbf{v}_2\rvert = \omega &&\text{(premise)},\end{align} $$

(5) $$ \begin{align} &\lvert E \cap \mathbf{v}_2\rvert = \omega &&\text{(by (1), (3) and (4))},\end{align} $$

(6) $$ \begin{align}&\mathbf{v} \trianglelefteq (D,E,F) &&\text{(by (3) and}\ (A,B,C)\mathrel{\trianglelefteq}(D,E,F)),\end{align} $$

(7) $$ \begin{align}&\lvert H \cap \mathbf{v}_2\rvert = \omega &&\text{(by (2), (5) and (6))}.\end{align} $$

Thus we have shown that both $(A,B,C)\mathrel {\trianglelefteq }(G,H,I)$ and

$$ \begin{align*} (\mathbf{v} \trianglelefteq (A,B,C) \& \lvert B \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert H \cap \mathbf{v}_2\rvert = \omega, \end{align*} $$

whence $(A,B,C)\mathrel {\prec _1}(G,H,I)$ also follows.

We pause to state another corollary we need towards our main lemma (Lemma 7).

Lemma 5. For arbitrary $(A,B,C), (D,E,F) \in W$ , the following statements hold:

1. 1. $\mathbf {v}\mathrel {\prec _1}(A,B,C)$ iff $\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$ and $\lvert B \cap \mathbf {v}_2\rvert = \omega $ .

2. 2. If both $\mathbf {v}\mathrel {\prec _1}(A,B,C)$ and $\mathbf {v}\mathrel {\prec _1}(D,E,F)$ , then

   $$ \begin{align*} (A,B,C)\mathrel{\prec_1}(D,E,F) \Leftrightarrow (A,B,C)\mathrel{\trianglelefteq}(D,E,F). \end{align*} $$

3. 3. If both $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ and $(D,E,F)\mathrel {\trianglelefteq }(A,B,C)$ , then $(A,B,C) = (D,E,F)$ .

Proof. (Part 1). We have $\mathbf {v}\mathrel {\prec _1}(A,B,C)$ iff $\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$ and

$$ \begin{align*} (\mathbf{v} \mathrel{\trianglelefteq} \mathbf{v} \,\&\, \lvert \mathbf{v}_2 \cap \mathbf{v}_2\rvert = \omega) \Rightarrow \lvert B \cap \mathbf{v}_2\rvert = \omega, \end{align*} $$

but, since the premise of the latter conditional is trivially true, it holds iff $\lvert B \cap \mathbf {v}_2\rvert = \omega $ .

(Part 2). By definition, $(A,B,C)\mathrel {\prec _1}(D,E,F)$ implies $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ . In the other direction, if $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ and, additionally, $\mathbf {v}\mathrel {\prec _1}(D,E,F)$ , then we must have, by Part 1, that $\lvert E \cap \mathbf {v}_2\rvert = \omega $ . But then also the conditional

$$ \begin{align*} (\mathbf{v} \trianglelefteq \mathbf{v} \& \lvert \mathbf{v}_2 \cap B\rvert = \omega) \Rightarrow \lvert E \cap \mathbf{v}_2\rvert = \omega \end{align*} $$

must be trivially true, whence also $(A,B,C)\mathrel {\prec _1}(D,E,F)$ follows.

(Part 3). If both $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ and $(D,E,F)\mathrel {\trianglelefteq }(A,B,C)$ then we have both $A = D$ and $C = F$ . Now $B = E$ follows by the fact that $(A,B,C), (D,E,F)$ are quasi-partitions.

In case we have $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ but $(A,B,C) \neq (D,E,F)$ , we will write $(A,B,C)\mathrel {\triangleleft }(D,E,F)$ .

Lemma 6. Fix a surjective $f: \mathbb {N} \to \mathbf {v}_2$ , and let $\sigma _1: W \to \mathscr {P}(\mathbb {N})$ and $\sigma _2: W \to \{0,1\}$ be defined as follows for all $(A,B,C) \in W$ :

$$ \begin{align*} \sigma_1(A,B,C):= \{n\mid f(n) \in A \}, \end{align*} $$

$$ \begin{align*} \sigma_2(A,B,C):= \begin{cases} 1,\text{ if } \mathbf{w}\mathrel{\triangleleft}(A,B,C),\\ 0,\text{ otherwise. } \end{cases} \end{align*} $$

Then $\sigma _1, \sigma _2$ are monotonic relative to $\trianglelefteq $ , and hence also relative to $\prec _i$ for all $i \in \{1,2\}$ .

Furthermore, we define that $\mathcal {M}^{\prime }_1 := (\mathcal {M}_1; R^1\mapsto \sigma _1)$ and $\mathcal {M}^{\prime }_2 := (\mathcal {M}_2; S^0\mapsto \sigma _2)$ . Then both $\mathcal {M}^{\prime }_1,\mathbf {v}\models \phi $ and $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \psi $ .

Proof. We deal with the monotonicity claims first. As for $\sigma _1$ , if $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ , and $n \in \sigma _1(A,B,C)$ , then $f(n) \in A \subseteq D$ , hence also $n \in \sigma _1(D,E,F)$ . As for $\sigma _2$ , if $(A,B,C)\mathrel {\trianglelefteq }(D,E,F)$ and $\sigma _2(A,B,C) = 1$ , then $\mathbf {w}\mathrel {\triangleleft }(A,B,C)$ , hence also $\mathbf {w}\mathrel {\triangleleft }(D,E,F)$ and $\sigma _2(D,E,F) = 1$ .

It remains to show the satisfaction claims for the extended models.

( $\mathcal {M}^{\prime }_1,\mathbf {v}\models \phi $ ). Assume that $(A,B,C) \in W$ is such that $\mathbf {v}\mathrel {\prec _1}(A,B,C)$ . Then, by Lemma 5.1, we have $\mathbf {v}\mathrel {\trianglelefteq }(A,B,C)$ and $\lvert B \cap \mathbf {v}_2\rvert = \omega $ . So we choose any $n \in B \cap \mathbf {v}_2$ and any $m \in \mathbb {N}$ such that $f(m) = n$ . Then $f(m) \notin A$ , and hence $m \notin \sigma _1(A,B,C)$ ; in other words, $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\not \models R(m)$ , whence $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\not \models \forall xR(x)$ and, by Expansion Property, $\mathcal {M}^{\prime }_1,(A, B, C)\not \models \forall xR(x)$ . Since the $\prec _1$ -successor to $\mathbf {v}$ was chosen arbitrarily, it follows, by Lemma 2, that $\mathcal {M}^{\prime }_1,\mathbf {v}\models \neg \forall xR(x)$ .

Next, if $n \in \mathbb {N}$ , then consider $f(n) \in \mathbf {v}_2$ . Clearly, we have $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models P(f(n))$ . If now $(A,B,C) \in W$ is such that $\mathbf {v}\mathrel {\prec _1}(A,B,C)$ and $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\models Q(f(n))$ , then $f(n) \in A$ , thus also $n \in \sigma _1(A,B,C)$ and, therefore, $(\mathcal {M}^{\prime }_1; \mathbb {N}),(A, B, C)\models R(n)$ . We have shown that $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models Q(f(n)) \to R(n)$ . Summing up, we get that $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models P(f(n)) \wedge (Q(f(n)) \to R(n))$ for arbitrary $n \in \mathbb {N}$ , therefore also $(\mathcal {M}^{\prime }_1; \mathbb {N}),\mathbf {v}\models \forall x\exists y(P(y) \wedge (Q(y) \to R(x)))$ and $\mathcal {M}^{\prime }_1,\mathbf {v}\models \forall x\exists y(P(y) \wedge (Q(y) \to R(x)))$ by Expansion Property.

( $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \psi $ ). Assume that $n \in \mathbb {N}$ and that $(A,B,C) \in W$ is such that $\mathbf {w}\mathrel {\trianglelefteq }(A,B,C)$ and $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models P(n)$ . Then two cases are possible:

Case 1. $\mathbf {w} = (A,B,C)$ . Then $n \in \mathbf {w}_1 \cup \mathbf {w}_2 = \mathbf {w}_1$ so that $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models Q(n)$ , whence also $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models Q(n) \vee S$ .

Case 2. $\mathbf {w}\mathrel {\triangleleft }(A,B,C)$ . Then $(\mathcal {M}^{\prime }_2; \mathbb {N}),(A, B, C)\models S$ , therefore also $(\mathcal {M}^{\prime }_2; \mathbb {N}), (A, B, C)\models Q(n) \vee S$ .

Summing up, we have shown that $(\mathcal {M}^{\prime }_2; \mathbb {N}),\mathbf {w}\models P(n) \to (Q(n) \vee S)$ for arbitrary $n \in \mathbb {N}$ , whence it follows that $(\mathcal {M}^{\prime }_2; \mathbb {N}),\mathbf {w}\models \forall x(P(x) \to (Q(x) \vee S))$ and, after applying Expansion Property, that $\mathcal {M}^{\prime }_2,\mathbf {w}\models \forall x(P(x) \to (Q(x) \vee S))$ . However, we also have $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models S$ by definition of $\sigma _2$ , and therefore $\psi $ fails at $(\mathcal {M}^{\prime }_2,\mathbf {w})$ .

Next, we define a particular bi-asimulation $\mathbb {A}$ between $\mathcal {M}_1$ and $\mathcal {M}_2$ such that we have $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$ . The definition looks as follows (cf. [12, Definition 7.3]).

Definition 4. Relative to the models ${\cal M}_1$ and ${\cal M}_2$ given in Definition 3, the relation $\mathbb {A}$ is defined as follows:

1. 1. $\mathbb {A} \subseteq \bigcup _{k \geq 0} [ (W \times \mathbb {N}^{k}) \times (W \times \mathbb {N}^{k})]$ ;

2. 2. Given any $(A,B,C), (D,E,F)\in W$ , any $n \geq 0$ and $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ we have $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , iff the following conditions hold:

   1. (a) Binary relation $[\bar {a}_n \mapsto \bar {b}_n]$ defines a bijection.

   2. (b) If $1 \leq k \leq n$ and $a_k \in A$ then $b_k \in D$ .

   3. (c) If $1 \leq k \leq n$ and $a_k \in B$ , then $b_k \in D \cup E$ .

Again, we start by pointing out some easy, but important consequences of our definition:

Corollary 2. For any $(A,B,C), (D,E,F)\in W$ , any $n \geq 0$ , and any $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ , if we have $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , then, for every $1 \leq k \leq n$ , we have

$$ \begin{align*} b_k \in F \Rightarrow a_k \in C. \end{align*} $$

Proof. Indeed, in the assumptions of the corollary we get the following chain of valid implications:

$$ \begin{align*} b_k \in F &\Rightarrow b_k \notin D \cup E &&\text{(by}\ F \cap (D \cup E) = \emptyset)\\ &\Rightarrow a_k \notin A \cup B &&\text{(by}\ (A,B,C)^{\frown}(\bar{a}_n)\mathrel{\mathbb{A}}(D,E,F)^{\frown}(\bar{b}_n))\\ &\Rightarrow a_k \in C&&\text{(by}\ \{\bar{a}_n\}\subseteq \mathbb{N}\ \text{and}\ A \cup B \cup C = \mathbb{N}).\\[-34pt] \end{align*} $$

Corollary 3. For any $(A,B,C), (D,E,F)\in W$ , any $n \geq 0$ , and any $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ , we have both $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ and $(D,E,F)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(A,B,C)^\frown (\bar {a}_n)$ iff the following conditions hold:

1. 1. Binary relation $[\bar {a}_n \mapsto \bar {b}_n]$ defines a bijection.

2. 2. For all $1 \leq k \leq n$ it is true that $a_k \in A$ iff $b_k \in D$ .

3. 3. For all $1 \leq k \leq n$ it is true that $a_k \in C$ iff $b_k \in F$ .

Proof. The $(\Rightarrow )$ -part follows from Corollary 2 and condition 2(b) of Definition 4.

For the $(\Leftarrow )$ -part, we observe that if $[\bar {a}_n \mapsto \bar {b}_n]$ defines a bijection, then $[\bar {b}_n \mapsto \bar {a}_n]$ also defines a bijection. The satisfaction of condition 2(b) of Definition 4 in both directions is then an immediate consequence of condition 2 of the Corollary, and as for Condition 2(c), we get that, if $1 \leq k \leq n$ and $a_k \in B$ , then $a_k \notin C$ , whence $b_k \notin F$ by condition 3 of the Corollary. Therefore, $b_k \in D\cup E$ . Similarly, if $b_k \in E$ , then $b_k \notin F$ , whence $a_k \notin C$ by condition 3 of the Corollary. But then $a_k \in A\cup B$

We can now make the crucial step towards our main result:

Lemma 7. The relation $\mathbb {A}$ , given in Definition 4, is a bi-asimulation between $\mathcal {M}_1$ and $\mathcal {M}_2$ , as given in Definition 3, and we have $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$ .

Proof. We check the satisfaction of the conditions given in Definition 1 by $\mathbb {A}$ . Condition (type) holds by Definition 4.1. Condition (atom) for P and Q follows from Definition 4.2(b) and (c). It is also clear that for any $w, v \in W$ we have $w\mathrel {\mathbb {A}}v$ , so that $\mathbb {A}$ is non-empty, and, in particular, $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$ holds. We check the remaining conditions in more detail:

Condition (back) . Let $i,j$ be such that $\{i, j\} = \{1,2\}$ , let $(A, B, C),(D,E,F)\in W$ , and let, for some $n \geq 0$ , $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ . Assume, moreover, that we have $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , and that some $(G,H,I) \in W$ is such that $(D,E,F)\mathrel {\prec _j}(G,H,I)$ (hence, in particular, $(D,E,F)\trianglelefteq (G,H,I)$ ). We have to consider two cases, since B can be either empty or infinite.

Case B1. $\lvert B\rvert = \omega $ . Then consider the triple $(J,K,L)$ such that:

$$ \begin{align*} J & = (A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G);\\ K & = (B \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](H);\\ L & = (C \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](I). \end{align*} $$

We will show that $(J,K,L)\in W$ and that we have $(A,B,C)\mathrel {\prec _i}(J,K,L)$ , $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$ , and $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$ . We break down the demonstration of this statement into the following series of claims:

Claim B 1.1. $J \cup K \cup L = \mathbb {N}$ .

Indeed, we know that

$$ \begin{align*} [\bar{b}_n \mapsto \bar{a}_n](G) \cup [\bar{b}_n \mapsto \bar{a}_n](H) \cup [\bar{b}_n \mapsto \bar{a}_n](I) &= [\bar{b}_n \mapsto \bar{a}_n](G \cup H \cup I)\\ &=[\bar{b}_n \mapsto \bar{a}_n](\mathbb{N}) = \{\bar{a}_n\} \end{align*} $$

since $(G,H,I)\in W$ and, therefore, $G \cup H \cup I = \mathbb {N}$ . On the other hand, we know that

$$ \begin{align*} (A \setminus \{\bar{a}_n\})\cup (B \setminus \{\bar{a}_n\})\cup (C \setminus \{\bar{a}_n\}) &= (A \cup B \cup C)\setminus \{\bar{a}_n\}\\ &= \mathbb{N}\setminus \{\bar{a}_n\} \end{align*} $$

since $(A,B,C)\in W$ and, therefore, $A \cup B \cup C = \mathbb {N}$ . Adding the two equalities together, we get that

$$ \begin{align*} J \cup K \cup L &= (\mathbb{N}\setminus \{\bar{a}_n\})\cup \{\bar{a}_n\} = \mathbb{N}, \end{align*} $$

as desired.

Claim B1.2. J, K, and L are infinite.

Indeed, A, B, and C are infinite, $\{\bar {a}_n\}$ is finite, and the following inclusions hold:

$$ \begin{align*} &A \setminus \{\bar{a}_n\} \subseteq J,\,B \setminus \{\bar{a}_n\} \subseteq K,\,C \setminus \{\bar{a}_n\} \subseteq L. \end{align*} $$

Claim B1.3. J, K, and L are pairwise disjoint.

Indeed, take J and K, for example. By definition, we have that $J \cap K$ is equal to

$$ \begin{align*}((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap ((B \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$

By application of distributivity laws, we further get that

$$ \begin{align*} J \cap K &= ((A \setminus \{\bar{a}_n\}) \cap (B \setminus \{\bar{a}_n\}))\cup\\ &\qquad\qquad\cup ((A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\qquad\qquad\cup ((B \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](G))\\ &\qquad\qquad\cup ([\bar{b}_n \mapsto \bar{a}_n](G) \cap [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$

Next, we know that $(A,B,C)\in W$ and, therefore, $A \cap B = \emptyset $ , which implies that $(A \setminus \{\bar {a}_n\})\cap (B \setminus \{\bar {a}_n\}) = \emptyset $ .

Moreover, we have

$$ \begin{align*}(A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H) \subseteq (A \setminus \{\bar{a}_n\}) \cap \{\bar{a}_n\} = \emptyset. \end{align*} $$

By a parallel argument, we can see that also $(B \setminus \{\bar {a}_n\}) \cap [\bar {b}_n \mapsto \bar {a}_n](G) = \emptyset $ .

Finally, we observe that $\bar {b}_n \mapsto \bar {a}_n$ is a bijection, and $(G,H,I)\in W$ and, therefore, $G \cap H = \emptyset $ , whence it follows that $[\bar {b}_n \mapsto \bar {a}_n](G) \cap [\bar {b}_n \mapsto \bar {a}_n](H) = \emptyset $ .

Summing up, we see that all the four sets in the union defining $J \cap K$ are empty and that we have that $J \cap K = \emptyset $ . The other cases are similar.

Claim B1.4. $(J,K,L)\in W$ .

By Claims B1.1–3.

Claim B1.5. $(A,B,C)\mathrel {\trianglelefteq }(J,K,L)$ .

Indeed, if $a \in A$ , and $a \notin \{\bar {a}_n\}$ , then $a \in J$ by definition of J. Otherwise we have both $a \in A$ and $a = a_k$ for some $1 \leq k \leq n$ , but then $b_k \in D$ by $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ . Next, note that $(D,E,F)\trianglelefteq (G,H,I)$ implies that $D \subseteq G$ , which means that $b_k \in G$ . But the latter means that $a = a_k \in [\bar {b}_n \mapsto \bar {a}_n](G) \subseteq J$ . Since $a \in A$ was chosen arbitrarily, we have shown that $A \subseteq J$ .

Next, if $a \in L$ , then either $a \in C \setminus \{\bar {a}_n\} \subseteq C$ , or $a \in [\bar {b}_n \mapsto \bar {a}_n](I)$ . In the latter case, $a = a_k$ for some $1 \leq k \leq n$ , and also $b_k \in I$ . Since $(D,E,F)\trianglelefteq (G,H,I)$ implies that $I \subseteq F$ , we get that $b_k \in F$ , but the latter means, by $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ and Corollary 2, that $a_k \in C$ . Since $a \in L$ was chosen arbitrarily, we have shown that $L \subseteq C$ .

Claim B1.6. $(\mathbf {v} \trianglelefteq (A,B,C)\,\&\,\lvert B \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert K \cap \mathbf {v}_2\rvert = \omega $ .

We observe that if $B \cap \mathbf {v}_2$ is infinite, then so is $(B \setminus \{\bar {a}_n\}) \cap \mathbf {v}_2$ , given that $\{\bar {a}_n\}$ is finite. But since, according to our definition of K, we have $(B \setminus \{\bar {a}_n\}) \subseteq K$ , $K \cap \mathbf {v}_2$ must be infinite, too.

Claim B1.7. $(A,B,C)\mathrel {\prec _i}(J,K,L)$ .

By Claims B1.5 and B1.6.

Claim B1.8. $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$ , and $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$ .

Indeed, for any given $1 \leq k \leq n$ , we have $a_k \in J$ iff $a_k \in [\bar {b}_n \mapsto \bar {a}_n](G)$ iff $b_k \in G$ , since $\bar {b}_n \mapsto \bar {a}_n$ defines a bijection. Similarly, we have $a_k \in L$ iff $a_k \in [\bar {b}_n \mapsto \bar {a}_n](I)$ iff $b_k \in I$ . But then our Claim follows from Corollary 3.

The correctness of our construction for Case B1 of condition (back) now follows from Claims B1.4, B1.7, and B1.8.

Case B2. $B = \emptyset $ . In this case, we partition $C \setminus \{\bar {a}_n\}$ into two disjoint infinite sets $C_1$ and $C_2$ , and define $(J,K,L)$ as follows:

$$ \begin{align*} J & = (A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G) ;\\ K & = C_1 \cup [\bar{b}_n \mapsto \bar{a}_n](H);\\ L & = C_2 \cup [\bar{b}_n \mapsto \bar{a}_n](I). \end{align*} $$

We will demonstrate the analogues of all the claims that we have made in the previous case.

Claim B2.1. $J \cup K \cup L = \mathbb {N}$ .

Again, we know that

$$ \begin{align*} [\bar{b}_n \mapsto \bar{a}_n](G) \cup [\bar{b}_n \mapsto \bar{a}_n](H) \cup [\bar{b}_n \mapsto \bar{a}_n](I) &= [\bar{b}_n \mapsto \bar{a}_n](G \cup H \cup I)\\ &=[\bar{b}_n \mapsto \bar{a}_n](\mathbb{N}) = \{\bar{a}_n\} \end{align*} $$

since $(G,H,I)\in W$ and, therefore, $G \cup H \cup I = \mathbb {N}$ . On the other hand, we know that

$$ \begin{align*} (A \setminus \{\bar{a}_n\})\cup C_1 \cup C_2 &= (A \setminus \{\bar{a}_n\}) \cup (C \setminus \{\bar{a}_n\})\\ &= (A \cup C)\setminus \{\bar{a}_n\} = \mathbb{N}\setminus \{\bar{a}_n\} \end{align*} $$

since $(A,B,C)\in W$ and $B = \emptyset $ and, therefore, $A \cup C = \mathbb {N}$ . Adding the two equalities together, we get that

$$ \begin{align*} J \cup K \cup L &= (\mathbb{N}\setminus \{\bar{a}_n\})\cup \{\bar{a}_n\} = \mathbb{N}, \end{align*} $$

as desired.

Claim B2.2. J, K, and L are infinite.

Indeed, A, $C_1$ , and $C_2$ are infinite, $\{\bar {a}_n\}$ is finite, and the following inclusions hold:

$$ \begin{align*} &A \setminus \{\bar{a}_n\} \subseteq J,\,C_1 \subseteq K,\,C_2 \subseteq L. \end{align*} $$

Claim B2.3. J, K, and L are pairwise disjoint.

Indeed, take J and K, for example. By definition, we have that

$$ \begin{align*} J \cap K &= ((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap (C_1 \cup [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\subseteq ((A \setminus \{\bar{a}_n\}) \cup [\bar{b}_n \mapsto \bar{a}_n](G)) \cap ((C \setminus \{\bar{a}_n\})\cup [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$

By application of distributivity laws, we further get that

$$ \begin{align*} J \cap K &\subseteq ((A \setminus \{\bar{a}_n\}) \cap (C \setminus \{\bar{a}_n\}))\cup\\ &\qquad\qquad\cup ((A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H))\\ &\qquad\qquad\cup ((C \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](G))\\ &\qquad\qquad\cup ([\bar{b}_n \mapsto \bar{a}_n](G) \cap [\bar{b}_n \mapsto \bar{a}_n](H)). \end{align*} $$

Next, we know that $(A,B,C)\in W$ and, therefore, $A \cap C = \emptyset $ , which implies that $(A \setminus \{\bar {a}_n\})\cap (C \setminus \{\bar {a}_n\}) = \emptyset $ .

Moreover, we have

$$ \begin{align*}(A \setminus \{\bar{a}_n\}) \cap [\bar{b}_n \mapsto \bar{a}_n](H) \subseteq (A \setminus \{\bar{a}_n\}) \cap \{\bar{a}_n\} = \emptyset. \end{align*} $$

By a parallel argument, we can see that also $(C \setminus \{\bar {a}_n\}) \cap [\bar {b}_n \mapsto \bar {a}_n](G) = \emptyset $ .

Finally, we observe that $\bar {b}_n \mapsto \bar {a}_n$ is a bijection, and $(G,H,I)\in W$ and, therefore, $G \cap H = \emptyset $ , whence it follows that $[\bar {b}_n \mapsto \bar {a}_n](G) \cap [\bar {b}_n \mapsto \bar {a}_n](H) = \emptyset $ .

Summing up, we see that all the four sets in the union extending $J \cap K$ are empty and that we have that $J \cap K = \emptyset $ . The other cases are similar.

Claim B2.4. $(J,K,L)\in W$ .

By Claims B2.1–3.

Claim B2.5. $(A,B,C)\mathrel {\trianglelefteq }(J,K,L)$ .

The argument for $A \subseteq J$ is exactly the same as in Case B1. To see that $L \subseteq C$ , note that $L = C_2 \cup [\bar {b}_n \mapsto \bar {a}_n](I) \subseteq (C \setminus \{\bar {a}_n\}) \cup [\bar {b}_n \mapsto \bar {a}_n](I)$ , so that the argument used for Case B1 is applicable also here.

Claim B2.6. $(\mathbf {v} \trianglelefteq (A,B,C)\,\&\,\lvert B \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert K \cap \mathbf {v}_2\rvert = \omega $ .

The claim holds trivially since $\lvert B \cap \mathbf {v}_2\rvert = \omega $ is falsified by the assumption of Case B2.

Claim B2.7. $(A,B,C)\mathrel {\prec _i}(J,K,L)$ .

By Claims B2.5 and B2.6.

Claim B2.8. $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$ , and $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$ .

Again the claim follows by the argument used for Claim B1.8 of Case B1.

Condition (forth). Let $i,j$ be such that $\{i, j\} = \{1,2\}$ , let $(A, B, C), (D,E,F)\in W$ , and let, for some $n \geq 0$ , $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ . Assume, moreover, that we have $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , and that some $(J,K,L) \in W$ is such that $(J,K,L)\mathrel {\prec _i}(A,B,C)$ (hence, in particular, $(A,B,C)\mathrel {\trianglerighteq }(J,K,L)$ ). Again, we have to consider two cases, since E can be either empty or infinite.

Case F1. $\lvert E\rvert = \omega $ . Then consider the triple $(G,H,I)$ such that:

$$ \begin{align*} G & = (D \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](J);\\ H & = (E \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](K);\\ I & = (F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L). \end{align*} $$

We will show that $(G,H,I)\in W$ and that we have $(G,H,I)\mathrel {\prec _j}(D,E,F)$ , $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$ , and $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$ . We break down the demonstration of this statement into our usual series of eight claims. The arguments, for the most part, just dualize the arguments given for Case B1 of condition (back), but we spell them out nonetheless.

Claim F1.1. $G \cup H \cup I = \mathbb {N}$ .

Indeed, we know that

$$ \begin{align*} [\bar{a}_n \mapsto \bar{b}_n](J) \cup [\bar{a}_n \mapsto \bar{b}_n](K) \cup [\bar{a}_n \mapsto \bar{b}_n](L) &= [\bar{a}_n \mapsto \bar{b}_n](J \cup K \cup L)\\ &=[\bar{a}_n \mapsto \bar{b}_n](\mathbb{N}) = \{\bar{b}_n\} \end{align*} $$

since $(J,K,L)\in W$ and, therefore, $J \cup K \cup L = \mathbb {N}$ . On the other hand, we know that

$$ \begin{align*} (D \setminus \{\bar{b}_n\})\cup (E \setminus \{\bar{b}_n\})\cup (F \setminus \{\bar{b}_n\}) &= (D \cup E \cup F)\setminus \{\bar{b}_n\}\\ &= \mathbb{N}\setminus \{\bar{b}_n\} \end{align*} $$

since $(D,E,F)\in W$ and, therefore, $D \cup E \cup F = \mathbb {N}$ . Adding the two equalities together, we get that

$$ \begin{align*} G \cup H \cup I &= (\mathbb{N}\setminus \{\bar{b}_n\})\cup \{\bar{b}_n\} = \mathbb{N}, \end{align*} $$

as desired.

Claim F1.2. G, H, and I are infinite.

Indeed, D, E, and F are infinite, $\{\bar {b}_n\}$ is finite, and the following inclusions hold:

$$ \begin{align*} &D \setminus \{\bar{b}_n\} \subseteq G,\,E \setminus \{\bar{b}_n\} \subseteq H ,\,F \setminus \{\bar{b}_n\} \subseteq I. \end{align*} $$

Claim F1.3. G, H, and I are pairwise disjoint.

Indeed, take G and H, for example. By definition, we have that $G \cap H$ is equal to

$$ \begin{align*}((D \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](J)) \cap ((E \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](K)), \end{align*} $$

By application of distributivity laws, we further get that

$$ \begin{align*} G \cap H &= ((D \setminus \{\bar{b}_n\}) \cap (E \setminus \{\bar{b}_n\}))\cup\\ &\qquad\qquad\cup ((D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](K))\\ &\qquad\qquad\cup ((E \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\qquad\qquad\cup ([\bar{a}_n \mapsto \bar{b}_n](J) \cap [\bar{a}_n \mapsto \bar{b}_n](K)). \end{align*} $$

Next, we know that $(D,E,F)\in W$ and, therefore, $D \cap E = \emptyset $ , which implies that $(D \setminus \{\bar {b}_n\})\cap (E \setminus \{\bar {b}_n\}) = \emptyset $ .

Moreover, we have

$$ \begin{align*}(D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](K) \subseteq (D \setminus \{\bar{b}_n\}) \cap \{\bar{b}_n\} = \emptyset. \end{align*} $$

By a parallel argument, we can see that also $(E \setminus \{\bar {b}_n\}) \cap [\bar {a}_n \mapsto \bar {b}_n](J) = \emptyset $ .

Finally, we observe that $\bar {a}_n \mapsto \bar {b}_n$ is a bijection, and $(J,K,L)\in W$ and, therefore, $J \cap K = \emptyset $ , whence it follows that $[\bar {a}_n \mapsto \bar {b}_n](J) \cap [\bar {a}_n \mapsto \bar {b}_n](K) = \emptyset $ .

Summing up, we see that all the four sets in the union defining $G \cap H$ are empty and that we have that $G \cap H = \emptyset $ . The other cases are similar.

Claim F1.4. $(G,H,I)\in W$ .

By Claims F1.1–3.

Claim F1.5. $(G,H,I)\mathrel {\trianglelefteq }(D,E,F)$ .

Indeed, if $b \in G$ , then either $b \in D \setminus \{\bar {b}_n\} \subseteq D$ , or $b \in [\bar {a}_n \mapsto \bar {b}_n](J)$ . In the latter case, $b = b_k$ for some $1 \leq k \leq n$ , and also $a_k \in J$ . Since $(J,K,L)\trianglelefteq (A,B,C)$ implies that $J \subseteq A$ , we get that $a_k \in A$ , but the latter means, by $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , that $b_k \in D$ . Since $b \in G$ was chosen arbitrarily, we have shown that $G \subseteq D$ .

Next, if $b \in F$ , and $b \notin \{\bar {b}_n\}$ , then $b \in I$ by definition of F. Otherwise we have both $b \in F$ and $b = b_k$ for some $1 \leq k \leq n$ , but then $a_k \in C$ by $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ and Corollary 2. Now, note that $(J,K,L)\mathrel {\trianglelefteq }(A,B,C)$ implies that $C \subseteq L$ , which means that $a_k \in L$ . But the latter means that $b = b_k \in [\bar {a}_n \mapsto \bar {b}_n](L) \subseteq I$ . Since $b \in F$ was chosen arbitrarily, we have shown that $F \subseteq I$ .

Claim F1.6. $(\mathbf {v} \trianglelefteq (G,H,I)\,\&\,\lvert H \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert E \cap \mathbf {v}_2\rvert = \omega $ .

We observe that if $H \cap \mathbf {v}_2$ is infinite, then so is $(E \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2$ , given that $H = (E \setminus \{\bar {b}_n\}) \cup [\bar {a}_n \mapsto \bar {b}_n](K)$ and $[\bar {a}_n \mapsto \bar {b}_n](K)$ is finite. But then $E \cap \mathbf {v}_2$ must be infinite, too.

Claim F1.7. $(G,H,I)\mathrel {\prec _j}(D,E,F)$ .

By Claims F1.5 and F1.6.

Claim F1.8. $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$ , and $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$ .

Indeed, for any given $1 \leq k \leq n$ , we have $b_k \in G$ iff $b_k \in [\bar {a}_n \mapsto \bar {b}_n](J)$ iff $a_k \in J$ , since $\bar {a}_n \mapsto \bar {b}_n$ defines a bijection. Similarly, we have $b_k \in I$ iff $b_k \in [\bar {a}_n \mapsto \bar {b}_n](L)$ iff $a_k \in L$ . But then our Claim follows from Corollary 3.

The correctness of our construction for Case 1 of condition (forth) now follows from Claims F1.4, F1.7, and F1.8.

Case F2. $E = \emptyset $ . In this case, we partition $D \setminus \{\bar {b}_n\}$ into two disjoint infinite sets $D_1$ and $D_2$ . Additionally, in case both $D \cap \mathbf {v}_1$ and $D \cap \mathbf {v}_2$ are infinite (which means that $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2$ and $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_1$ are infinite, too), we ensure that we have $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_2 \subseteq D_1$ and $(D \setminus \{\bar {b}_n\}) \cap \mathbf {v}_1 \subseteq D_2$ . Then we define $(G,H,I)$ as follows:

$$ \begin{align*} G & = D_1 \cup [\bar{a}_n \mapsto \bar{b}_n](J);\\ H & = D_2 \cup [\bar{a}_n \mapsto \bar{b}_n](K);\\ I & = (F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L). \end{align*} $$

We will demonstrate our usual eight claims in some detail again, even though the arguments mostly dualize the proofs given for the respective claims in Case B2 of condition (back) (Claim F2.6 being, perhaps, the only exception to this rule).

Claim F2.1. $G \cup H \cup I = \mathbb {N}$ .

Again, we know that

$$ \begin{align*} [\bar{a}_n \mapsto \bar{b}_n](J) \cup [\bar{a}_n \mapsto \bar{b}_n](K) \cup [\bar{a}_n \mapsto \bar{b}_n](L) &= [\bar{a}_n \mapsto \bar{b}_n](J \cup K \cup L)\\ &=[\bar{a}_n \mapsto \bar{b}_n](\mathbb{N}) = \{\bar{b}_n\} \end{align*} $$

since $(J,K,L)\in W$ and, therefore, $J \cup K \cup L = \mathbb {N}$ . On the other hand, we know that

$$ \begin{align*} (F \setminus \{\bar{b}_n\})\cup D_1 \cup D_2 &= (F \setminus \{\bar{b}_n\}) \cup (D \setminus \{\bar{b}_n\})\\ &= (F \cup D)\setminus \{\bar{b}_n\} = \mathbb{N}\setminus \{\bar{b}_n\} \end{align*} $$

since $(D,E,F)\in W$ and $E = \emptyset $ and, therefore, $D \cup F = \mathbb {N}$ . Adding the two equalities together, we get that

$$ \begin{align*} G \cup H \cup I &= (\mathbb{N}\setminus \{\bar{b}_n\})\cup \{\bar{b}_n\} = \mathbb{N}, \end{align*} $$

as desired.

Claim F2.2. G, H, and I are infinite.

Indeed, $D_1$ , $D_2$ , and F are infinite, $\{\bar {b}_n\}$ is finite, and the following inclusions hold:

$$ \begin{align*} &D_1 \subseteq G,\,D_2 \subseteq H,\,F \setminus \{\bar{b}_n\} \subseteq I. \end{align*} $$

Claim F2.3. G, H, and I are pairwise disjoint.

Indeed, take G and I, for example. By definition, we have that

$$ \begin{align*} G \cap I &= ((F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L)) \cap (D_1 \cup [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\subseteq ((F \setminus \{\bar{b}_n\}) \cup [\bar{a}_n \mapsto \bar{b}_n](L)) \cap ((D \setminus \{\bar{b}_n\})\cup [\bar{a}_n \mapsto \bar{b}_n](J)). \end{align*} $$

By application of distributivity laws, we further get that

$$ \begin{align*} G \cap I &\subseteq ((F \setminus \{\bar{b}_n\}) \cap (D \setminus \{\bar{b}_n\}))\cup\\ &\qquad\qquad\cup ((F \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J))\\ &\qquad\qquad\cup ((D \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](L))\\ &\qquad\qquad\cup ([\bar{a}_n \mapsto \bar{b}_n](J) \cap [\bar{a}_n \mapsto \bar{b}_n](L)). \end{align*} $$

Next, we know that $(D,E,F)\in W$ and, therefore, $D \cap F = \emptyset $ , which implies that $(D \setminus \{\bar {b}_n\})\cap (F \setminus \{\bar {b}_n\}) = \emptyset $ .

Moreover, we have

$$ \begin{align*}(F \setminus \{\bar{b}_n\}) \cap [\bar{a}_n \mapsto \bar{b}_n](J) \subseteq (F \setminus \{\bar{b}_n\}) \cap \{\bar{b}_n\} = \emptyset. \end{align*} $$

By a parallel argument, we can see that also $(D \setminus \{\bar {b}_n\}) \cap [\bar {a}_n \mapsto \bar {b}_n](L) = \emptyset $ .

Finally, we observe that $\bar {a}_n \mapsto \bar {b}_n$ is a bijection, and $(J,K,L)\in W$ and, therefore, $J \cap L = \emptyset $ , whence it follows that $[\bar {a}_n \mapsto \bar {b}_n](J) \cap [\bar {a}_n \mapsto \bar {b}_n](L) = \emptyset $ .

Summing up, we see that all the four sets in the union extending $G \cap I$ are empty and that we have $G \cap I = \emptyset $ . The other cases are similar.

Claim F2.4. $(G,H,I)\in W$ .

By Claims F2.1–3.

Claim F2.5. $(G,H,I)\mathrel {\trianglelefteq }(D,E,F)$ .

The argument for $F \subseteq I$ is exactly the same as in Case 1. To see that $G \subseteq D$ , note that $G = D_1 \cup [\bar {a}_n \mapsto \bar {b}_n](J) \subseteq (D \setminus \{\bar {b}_n\}) \cup [\bar {a}_n \mapsto \bar {b}_n](J)$ , so that the argument used for Case F1 is applicable also here.

Claim F2.6. $(\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)\,\&\,\lvert H \cap \mathbf {v}_2\rvert = \omega ) \Rightarrow \lvert E \cap \mathbf {v}_2\rvert = \omega $ .

Since we suppose that $E = \emptyset $ , it will suffice to show that assuming both $\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)$ and $\lvert H \cap \mathbf {v}_2\rvert = \omega $ will lead us to a contradiction. Indeed, if $\mathbf {v} \mathrel {\trianglelefteq }(G,H,I)$ , then, in particular, $\mathbf {v}_1 \subseteq G$ , so that $\lvert G \cap \mathbf {v}_1\rvert = \omega $ . But we have $G = D_1 \cup [\bar {a}_n \mapsto \bar {b}_n](J)$ and $[\bar {a}_n \mapsto \bar {b}_n](J)$ is finite; therefore, both $\mathbf {v}_1 \cap D_1$ , and its superset, $\mathbf {v}_1 \cap D$ , must be infinite.

If also $\lvert H \cap \mathbf {v}_2\rvert = \omega $ , then a parallel argument shows that also $\mathbf {v}_2 \cap D_2$ and $\mathbf {v}_2 \cap D$ are infinite.

But, since both $\mathbf {v}_1 \cap D$ and $\mathbf {v}_2 \cap D$ are infinite, we must have, by the choice of $D_1$ and $D_2$ , that $\mathbf {v}_2 \cap (D \setminus \{\bar {b}_n\}) \subseteq D_1$ . On the other hand, $D_2 \subseteq (D \setminus \{\bar {b}_n\})$ implies that $D_2 = D_2 \cap (D \setminus \{\bar {b}_n\})$ .

Therefore,

$$ \begin{align*}\mathbf{v}_2 \cap D_2 = \mathbf{v}_2 \cap (D \setminus \{\bar{b}_n\})\cap D_2 \subseteq D_1 \cap D_2 = \emptyset. \end{align*} $$

Since we have $H = D_2 \cup [\bar {a}_n \mapsto \bar {b}_n](K)$ , and $[\bar {a}_n \mapsto \bar {b}_n](K)$ is clearly finite, the set $H \cap \mathbf {v}_2$ can be at most finite, which is a contradiction.

Claim F2.7. $(G,H,I)\mathrel {\prec _j}(D,E,F)$ .

By Claims F2.5 and F2.6.

Claim F2.8. $(J,K,L)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(G,H,I)^\frown (\bar {b}_n)$ , and $(G,H,I)^\frown (\bar {b}_n)\mathrel {\mathbb {A}}(J,K,L)^\frown (\bar {a}_n)$ .

Again the claim follows by the argument used for Claim F1.8 of Case F1.

Condition (left). Let $i,j$ be such that $\{i, j\} = \{1,2\}$ , let $(A, B, C), (D,E,F)\in W$ , and let, for some $n \geq 0$ , $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ . Assume, moreover, that we have $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , and that $b \in \mathbb {N}$ . If $b = b_k$ for some $1 \leq k \leq n$ , then we set $a: = a_k$ . Otherwise, given that $b \notin \{\bar {b}_n\}$ , we choose any $a \in C \setminus \{\bar {a}_n\}$ . We can do this since C is infinite and $\{\bar {a}_n\}$ is finite. In both cases we get that $(A,B,C)^\frown (\bar {a}_n)^\frown (a)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)^\frown (b)$ by definition of $\mathbb {A}$ .

Condition (right). Let $i,j$ be such that $\{i, j\} = \{1,2\}$ , let $(A, B, C), (D,E,F)\in W$ , and let, for some $n \geq 0$ , $\bar {a}_n, \bar {b}_n \in \mathbb {N}^{n}$ . Assume, moreover, that we have $(A,B,C)^\frown (\bar {a}_n)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)$ , and that $a \in \mathbb {N}$ . If $a = a_k$ for some $1 \leq k \leq n$ , then we set $b: = b_k$ . Otherwise, given that $a \notin \{\bar {a}_n\}$ , we choose any $b \in D \setminus \{\bar {b}_n\}$ . We can do this since D is infinite and $\{\bar {b}_n\}$ is finite. In both cases we get that $(A,B,C)^\frown (\bar {a}_n)^\frown (a)\mathrel {\mathbb {A}}(D,E,F)^\frown (\bar {b}_n)^\frown (b)$ by definition of $\mathbb {A}$ .

At this point, it only remains to reap the fruits of the tedious work towards the host of previous lemmas and corollaries:

Theorem 2. $\mathsf {FOBIL}$ fails CIP.

Proof. Indeed, we have $\models \phi \to \psi $ and $\Theta _\phi \cap \Theta _\psi = \Sigma $ . If now $\theta \in L_\emptyset (\Sigma )$ is such that both $\models \phi \to \theta $ and $\models \theta \to \psi $ , then, by Lemma 6, we must have both $\mathcal {M}^{\prime }_1,\mathbf {v}\models \theta $ and $\mathcal {M}^{\prime }_2,\mathbf {w}\not \models \theta $ . We also have $\mathcal {M}_i = \mathcal {M}^{\prime }_i\upharpoonright \Sigma $ for $i \in \{1,2\}$ and, therefore, by Expansion Property, we get that $\mathcal {M}_1,\mathbf {v}\models \theta $ and $\mathcal {M}_2,\mathbf {w}\not \models \theta $ . On the other hand, we know, by Lemma 7, that the relation $\mathbb {A}$ , given in Definition 4, is a bi-asimulation between $\mathcal {M}_1$ and $\mathcal {M}_2$ and that we have $\mathbf {v}\mathrel {\mathbb {A}}\mathbf {w}$ . Therefore, $\mathcal {M}_1,\mathbf {v}\models \theta $ implies, by Lemma 3, that $\mathcal {M}_2,\mathbf {w}\models \theta $ . The obtained contradiction shows that no interpolant exists for $\phi \to \psi $ .

Remark 3. Note that Lemma 5.1–2 implies that the submodels generated by $\mathbf {v}$ and $\mathbf {w}$ in $\mathcal {M}_1$ and $\mathcal {M}_2$ , respectively, are exactly the models $\mathcal {M}_1$ and $\mathcal {M}_2$ as given in [12, Definition 7.2]. Moreover, the proof of Lemma 7 re-uses the constructions given in the proof of [12, Lemma 7.2] except for the part treating condition (forth) of Definition 1. However, the arguments showing the correctness of these constructions had to be given anew, since the models $\mathcal {M}_1$ and $\mathcal {M}_2$ are not bi-intuitionistically equivalent to the models of [12, Definition 7.2].

Thus our main construction in this paper is, in a very precise sense, just an extension of the main construction given in [12, Section 7].

4 Conclusion

In this article we have refuted the Craig Interpolation Property for predicate bi-intuitionistic logic, showing how different the situation is from the propositional case that was solved positively in [9]. We proved that Mints’s counterexample [12] for predicate intuitionitic logic with constant domains also did the work in the present context. It is clear that, although we allowed constants in our presentation, their role is purely technical, and that due to the nature of Mints’s counterexample, we have also disproved CIP for the purely relational variant of $\mathsf {FOBIL}$ . The present work still leaves some related open questions, such as the status of the Beth definability property in the bi-intuitionistic setting. For the time being, we have left these and other similar matters as topics for future research.