Article contents
SUBJECT-MATTER AND INTENSIONAL OPERATORS III: STATE-SENSITIVE SUBJECT-MATTER AND TOPIC SUFFICIENCY
Published online by Cambridge University Press: 12 July 2023
Abstract
Logical frameworks that are sensitive to features of sentences’ subject-matter—like Berto’s topic-sensitive intentional modals (TSIMs)—demand a maximally faithful model of the topics of sentences. This is an especially difficult task in the case in which topics are assigned to intensional formulae. In two previous papers, a framework was developed whose model of intensional subject-matter could accommodate a wider range of intuitions about particular intensional conditionals. Although resolving a number of counterintuitive features, the work made an implicit assumption that the subject-matter of an intensional conditional is a function of the subject-matters of its subformulae. This assumption—which I will call a principle of topic sufficiency—runs counter to some natural intuitions concerning topic. In this paper, we will investigate topic sufficiency and offer a semantic account that is state-sensitive, providing an implementation through the introduction of topic-sensitive logics related to William Parry’s prototypical 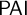 $\mathsf {PAI}$.
$\mathsf {PAI}$.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
BIBLIOGRAPHY
- 9
- Cited by


