Article contents
WHAT MODEL COMPANIONSHIP CAN SAY ABOUT THE CONTINUUM PROBLEM
Published online by Cambridge University Press: 25 April 2023
Abstract
We present recent results on the model companions of set theory, placing them in the context of a current debate in the philosophy of mathematics. We start by describing the dependence of the notion of model companionship on the signature, and then we analyze this dependence in the specific case of set theory. We argue that the most natural model companions of set theory describe (as the signature in which we axiomatize set theory varies) theories of 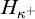 $H_{\kappa ^+}$, as
$H_{\kappa ^+}$, as 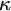 $\kappa $ ranges among the infinite cardinals. We also single out
$\kappa $ ranges among the infinite cardinals. We also single out 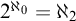 $2^{\aleph _0}=\aleph _2$ as the unique solution of the continuum problem which can (and does) belong to some model companion of set theory (enriched with large cardinal axioms). While doing so we bring to light that set theory enriched by large cardinal axioms in the range of supercompactness has as its model companion (with respect to its first order axiomatization in certain natural signatures) the theory of
$2^{\aleph _0}=\aleph _2$ as the unique solution of the continuum problem which can (and does) belong to some model companion of set theory (enriched with large cardinal axioms). While doing so we bring to light that set theory enriched by large cardinal axioms in the range of supercompactness has as its model companion (with respect to its first order axiomatization in certain natural signatures) the theory of 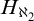 $H_{\aleph _2}$ as given by a strong form of Woodin’s axiom
$H_{\aleph _2}$ as given by a strong form of Woodin’s axiom  $(*)$ (which holds assuming
$(*)$ (which holds assuming 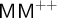 $\mathsf {MM}^{++}$). Finally this model-theoretic approach to set-theoretic validities is explained and justified in terms of a form of maximality inspired by Hilbert’s axiom of completeness.
$\mathsf {MM}^{++}$). Finally this model-theoretic approach to set-theoretic validities is explained and justified in terms of a form of maximality inspired by Hilbert’s axiom of completeness.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
BIBLIOGRAPHY
- 3
- Cited by


