Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T15:39:48.446Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributed collaborative 3D pose estimation of robots from heterogeneous relative measurements: an optimization on manifold approach

Published online by Cambridge University Press:  10 April 2014

Joseph Knuth  and
Prabir Barooah
Joseph Knuth*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL, USA
Prabir Barooah
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL, USA
*
*Corresponding author. E-mail: knuth@ufl.edu
Get access Rights & Permissions [Opens in a new window]

Summary

We propose a distributed algorithm for estimating the 3D pose (position and orientation) of multiple robots with respect to a common frame of reference when Global Positioning System is not available. This algorithm does not rely on the use of any maps, or the ability to recognize landmarks in the environment. Instead, we assume that noisy relative measurements between pairs of robots are intermittently available, which can be any one, or combination, of the following: relative pose, relative orientation, relative position, relative bearing, and relative distance. The additional information about each robot's pose provided by these measurements are used to improve over self-localization estimates. The proposed method is similar to a pose-graph optimization algorithm in spirit: pose estimates are obtained by solving an optimization problem in the underlying Riemannian manifold 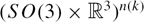$(SO(3)\times{\mathcal R}^3)^{n(k)}$. The proposed algorithm is directly applicable to 3D pose estimation, can fuse heterogeneous measurement types, and can handle arbitrary time variation in the neighbor relationships among robots. Simulations show that the errors in the pose estimates obtained using this algorithm are significantly lower than what is achieved when robots estimate their pose without cooperation. Results from experiments with a pair of ground robots with vision-based sensors reinforce these findings. Further, simulations comparing the proposed algorithm with two state-of-the-art existing collaborative localization algorithms identify under what circumstances the proposed algorithm performs better than the existing methods. In addition, the question of trade-offs between cost (of obtaining a certain type of relative measurement) and benefit (improvement in localization accuracy) for various types of relative measurements is considered.

Keywords

Robot localizationMulti-robot systemsComputer visionMobile robotsSLAM
Type
Articles
Information
Robotica , Volume 33 , Issue 7 , August 2015 , pp. 1507 - 1535
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Absil, P., Mahony, R. and Sepulchre, R., Optimization Algorithms on Matrix Manifolds (Princeton University Press, Princeton, NJ, 2008).Google Scholar
2. Andersson, L. A. A. and Nygards, J., “C-SAM: Multi-Robot SLAM Using Square Root Information Smoothing,” Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, California, USA (May 19–23, 2008) pp. 2798–2805.Google Scholar
3. Aragues, R., Carlone, L., Calafiore, G. and Sagues, C., “Multi-Agent Localization from Noisy Relative Pose Measurements,” Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China (May 9–13, 2011) pp. 364–369.Google Scholar
4. Barooah, P., Russell, W. J. and Hespanha, J. P., “Approximate Distributed Kalman Filtering for Cooperative Multi-Agent Localization,” Proceedings of the International Conference in Distributed Computing in Sensor Systems (DCOSS), Santa Barbara, CA (Jun. 2010) pp. 102–115.Google Scholar
5. Boyd, S. and Vandenberghe, L., Convex Optimization (Cambridge University Press, Cambridge, UK, 2004).Google Scholar
6. Breckenridge, W. G., “Quaternions Proposed Standard Conventions,” Technical Report, Jet Propulsion Laboratory, Pasadena, CA (1999), Interoffice Memorandum IOM 343-79-1199.Google Scholar
7. Caglioti, V., Citterio, A. and Fossati, A., “Cooperative, Distributed Localization in Multi-Robot Systems: A Minimum-Entropy Approach,” Proceedings of the IEEE Workshop on Distributed Intelligent Systems, Czech Republic (Jun. 15–16, 2006) pp. 25–30.Google Scholar
8. Fox, D., Burgard, W., Kruppa, H. and Thrun, S., “A probabilistic approach to collaborative multi-robot localization,” Auton Robots 8 (3), 325–344 (2000).Google Scholar
9. Gallot, S., Hulin, D. and LaFontaine, J., Riemannian Geometry, 3rd ed. (Springer, New York, NY, 2004). ISBN: 3540204938.Google Scholar
10. Grisetti, G., Grzonka, S., Stachniss, C., Pfaff, P., and Burgard, W. “Efficient Estimation of Accurate Maximum Likelihood Maps in 3D,” Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, California (Oct. 29, 2007–Nov. 2, 2007) pp. 3472–3478.Google Scholar
11. Grove, K., Karcher, H. and Ruh, E. A., “Jacobi fields and Finsler metrics on compact Lie groups with an application to differentiable pinching problems,” Math. Ann. 211, 7–21 (1974).Google Scholar
12. Howard, A., “Multi-robot simultaneous localization and mapping using particle filters,” Int. J. Robot. Res. 25 (12), 1243–1256 (Aug. 2006).Google Scholar
13. Howard, A., Matark, M. and Sukhatme, G., “Localization for mobile robot teams using maximum likelihood estimation,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland (Sep. 2002) vol. 1, pp. 434–439.Google Scholar
14. Indelman, V., Gurfil, P., Rivlin, E. and Rotstein, H., “Distributed Vision-Aided Cooperative Localization and Navigation Based on Three-View Geometry,” IEEE Aerospace Conference, Big Sky, MT (Mar. 5–12, 2011) pp. 1–20.Google Scholar
15. Kim, B., Kaess, M., Fletcher, L., Leonard, J., Bachrach, A., Roy, N. and Teller, S., “Multiple Relative Pose Graphs for Robust Cooperative Mapping,” Proceedings of the International Conference on Robotics and Automation (ICRA), Anchorage, Alaska (2010), pp. 3185–3192.Google Scholar
16. Knuth, J., “A Study of Single and Multi-Robot Localization: A Manifold Approach,” PhD Thesis, University of Florida (Apr. 2013).Google Scholar
17. Knuth, J. and Barooah, P., “Distributed Collaborative Localization of Multiple Vehicles from Relative Pose Measurements,” Proceedings of the 47th Annual Allerton Conference on Communication, Control, and Computing, Allerton, IL (Oct. 2009), pp. 314–321. doi:10.1109/ALLERTON.2009.5394785.Google Scholar
18. Knuth, J. and Barooah, P., “Collaborative 3D Localization of Robots from Relative Pose Measurements Using Gradient Descent on Manifolds,” Proceedings of the IEEE International Conference on Robotics and Automation, St. Paul, MN (May 2012) pp. 1101–1106.Google Scholar
19. Knuth, J. and Barooah, P., “Error growth in position estimation from noisy relative pose measurements,” Robot. Auton. Syst. 61 (3), 229–244 (Mar. 2013).Google Scholar
20. Kummerle, R., Grisetti, G., Strasdat, H., Konolige, K. and Burgard, W., “g2o: A General Framework for Graph Optimization,” Proceedings of the ICRA 2011, Shanghai, China (Feb. 2011), pp. 1–7.Google Scholar
21. Leung, K. Y., Barfoot, T. and Liu, H., “Decentralized localization of sparsely communicating robot networks: A centralized-equivalent approach,” IEEE Trans. Robot. 26 (1), 62–77 (2010).Google Scholar
22. Long, A., Wolfe, K., Mashner, M. and Chirikjian, G., “The Banana Distribution is Gaussian: A Localization Study with Exponential Coordinates,” 2012 Robotics: Science and Systems Conference, University of Sydney, Sydney, NSW (Jul. 2012).Google Scholar
23. Ma, Y., Košecká, J. and Sastry, S., “Optimization Criteria and Geometric Algorithms for Motion and Structure Estimation,” Int. J. Comput. Vis. 44 (3), 219–249 (2001).Google Scholar
24. Mardia, K. V. and Jupp, P. E., Directional Statistics, Wiley Series in Probability and Statistics (Wiley, River Street Hoboken, NJ, 2000).Google Scholar
25. Martinelli, A., Pont, F. and Siegwart, R., “Multi-Robot Localization Using Relative Observations,” Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain (Apr. 18–22, 2005).Google Scholar
26. Melnyk, I. V., Hesch, J. A. and Roumeliotis, S. I., “Cooperative Vision-Aided Inertial Navigation Using Overlapping Views,” IEEE International Conference on Robotics and Automation, St. Paul, MN (2012) pp. 936–943.Google Scholar
27. Nerurkar, E., Roumeliotis, S. and Martinelli, A., “Distributed Maximum a Posteriori Estimation for Multi-Robot Cooperative Localization,” IEEE International Conference on Robotics and Automation, Kobe, Japan (May 2009), pp. 1402–1409.Google Scholar
28. Ni, K., Steedly, D., and Dellaert, F., “Tectonic SAM: Exact, Out-of-Core, Submap-Based SLAM,” Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy (Apr. 10–14, 2007) pp. 1678–1685.Google Scholar
29. Olson, C. F., Matthies, L. H., Schoppers, M. and Maimone, M. W., “Rover navigation using stereo ego-motion,” Robot. Auton. Syst. 43 (4), 215–229 (Jun. 2003).Google Scholar
30. Panzieri, S., Pascucci, F. and Setola, R., “Multirobot Localisation Using Interlaced Extended Kalman Filter,” Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. (IEEE, New York, NY, 2006) pp. 2816–2821. doi:10.1109/IROS.2006.282065.Google Scholar
31. Rekleitis, I., Dudek, G. and Milios, E., “Multi-robot Cooperative Localization: A Study of Trade-Offs between Efficiency and Accuracy,” IEEE/RSJ International Conference on Intelligent Robots and Systems, EPFL, Switzerland (Sep. 2002), vol. 3, pp. 2690–2695.Google Scholar
32. Roumeliotis, S. and Bekey, G., “Distributed multirobot localization,” IEEE Trans. Robot. Autom. 18 (5), 781–795 (Oct. 2002).Google Scholar
33. Sanderson, C., “A distributed algorithm for cooperative navigation among multiple mobile robots,” Adv. Robot. 12 (4), 335–349 (1998).Google Scholar
34. Sibley, G., Mei, C., Reid, I. and Newman, P., “Adaptive Relative Bundle Adjustment,” In: Robotics: Science and Systems (RSS), University of Washington, Seattle, WA (MIT Press, Cambridge, MA, 2009).Google Scholar
35. Tron, R. and Vidal, R., “Distributed Image-Based 3-D Localization of Camera Sensor Networks,” Proceedings of the IEEE Conference on Decision and Control, Shanghai, China (Dec. 15–18, 2009) pp. 901–908.Google Scholar
36. Wolfe, K. C., Mashner, M. and Chirikjian, G. S., “Bayesian fusion on Lie groups,” J. Algebr. Stat. 2 (1), 75–97 (2011).Google Scholar
37. Yershova, A., Jain, S., LaValle, S. and Mitchell, J., “Generating uniform incremental grids on SO(3) using the Hopf fibration,” Int. J. Robot. Res. 29 (7) (2010) pp. 801–812.Google Scholar