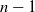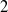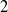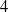1. Introduction
1.1. Motivations and state of the art
Under-actuated systems are a particular class of dynamic systems in which one or more joints are not equipped with motors but are connected to the rest of the kinematic chain only by means of springs (elastic joints). Actually, the motor torques of the actuated joints can indirectly control the motion of the elastic joints.
In the last years, there has been a significant growth in research on under-actuated systems, resulting in the development of various applications for different purposes. There are jointed arm under-actuated robots [Reference Agrawal and Sangwan1–Reference Qin, Ji, Cheng, Zhao, Pan, Shi and Song3], cable-driven under-actuated robots [Reference Barbazza, Zanotto, Rosati and Agrawal4, Reference Zanotto, Rosati and Agrawal5], and under-actuated walking robots [Reference Gupta and Kumar6, Reference He, Wang and Liu7].
The jointed arm under-actuated robots are more appealing than fully actuated robots when the weight and the cost of the robot are important issues. Moreover, increasing the DOF with the same number of actuators increases robot dexterity, reducing the risk of collision [Reference Bottin, Boschetti and Rosati8, Reference Tonan, Doria, Bottin and Rosati9]. Other noteworthy examples of under-actuated systems include a prosthetic device as detailed in ref. [Reference Loutan and Persad10], an autonomous sea surface launch, and recovery robot presented in [Reference Angelini, Ida’, Bertin, Carricato, Mantovani, Bazzi and Orassi11], and innovative gripper designs discussed in ref. [Reference Becedas, Payo and Feliu12–Reference Okken, Dekker, de Jong and Brouwer14]. In general, under-actuated systems are hard to control. Over the years, many solutions have been proposed to overcome their limitations, recent solutions can be found in ref. [Reference Bettega, Richiedei, Tamellin and Trevisani15, Reference Xin, Wang and Liu16].
The differential flatness is an interesting property of some dynamic systems that was discovered some years ago [Reference Sira-Ramirez and Agrawal17] to gain the controllability of the system. In a differentially flat system, the state variables can be expressed as functions of a privileged set of variables, which are named flat variables [Reference Murray, Rathinam and Sluis18]. The mathematical operation that allows the mapping from the state variables to the flat variables is named diffeomorphism. Most of the applications of differential flatness refer to the control of linear time-invariant dynamic systems [Reference Yong, Paden and Frazzoli19, Reference Zanotto, Rosati and Agrawal20], but there are interesting applications in the field of the control of non-linear systems as well [Reference Mounier and Rudolph21, Reference Ryu and Agrawal22].
The concept of differential flatness is useful for planning point-to-point motions of under-actuated robots built with specific inertia properties [Reference Franch, Agrawal and Sangwan23]. The necessary and sufficient conditions under which an under-actuated
![]() $n-$
DOF planar jointed robot arm with one or two actuators is differential flat were presented in ref. [Reference Franch, Agrawal and Sangwan23]. This analysis was extended in ref. [Reference Franch, Reyes and Agrawal24] for
$n-$
DOF planar jointed robot arm with one or two actuators is differential flat were presented in ref. [Reference Franch, Agrawal and Sangwan23]. This analysis was extended in ref. [Reference Franch, Reyes and Agrawal24] for
![]() $n-$
DOF planar jointed arm robots with an arbitrary number of actuators. Many simulations and experimental tests have demonstrated the validity of the control of under-actuated robots based on flat variables, but have highlighted the presence of some mechanical phenomena that usually are not taken into account in the model of the under-actuated robot based on flat variables. In particular, in ref. [Reference Sangwan, Kuebler and Agrawal25] the presence of friction in the gearbox of the actuated joint was detected and a controller with a torque inner loop was developed, to compensate for friction. In ref. [Reference Bottin and Rosati26], the vibrations of an under-actuated robot at given configurations were analyzed, taking into account the effect of the compliance of the actuated joints.
$n-$
DOF planar jointed arm robots with an arbitrary number of actuators. Many simulations and experimental tests have demonstrated the validity of the control of under-actuated robots based on flat variables, but have highlighted the presence of some mechanical phenomena that usually are not taken into account in the model of the under-actuated robot based on flat variables. In particular, in ref. [Reference Sangwan, Kuebler and Agrawal25] the presence of friction in the gearbox of the actuated joint was detected and a controller with a torque inner loop was developed, to compensate for friction. In ref. [Reference Bottin and Rosati26], the vibrations of an under-actuated robot at given configurations were analyzed, taking into account the effect of the compliance of the actuated joints.
The extension of the differential flatness concepts to under-actuated robots with viscous friction has been performed by Sangwan and Agrawal in 2018 [Reference Sangwan and Agrawal27]. On the one hand, the exact introduction of viscous friction leads to a great complication in the mathematical model. On the other hand, friction in robots and automatic machines is a complex non-linear phenomenon [Reference Agrawal and Sangwan28] that sometimes is simplified considering an equivalent viscous friction [Reference Canudas de Wit, Olsson, Astrom and Lischinsky29]. More detailed friction models have been developed for applications requiring high-precision motions [Reference Astrom and Canudas-De-Wit30, Reference Genta and Amati31]. Nonetheless, friction effects are typically eliminated or compensated by means of specifically designed controllers [Reference Liu, Huda, Sun and Yu32]. In ref. [Reference Lee, Tan and Huang33], a new compensation technique for the dynamic friction based on a PD control scheme was presented. Other researchers in [Reference Na, Chen, Ren and Guo34] proposed a continuously differentiable friction model to account for the friction non-linearities.
Another technique was presented in ref. [Reference Martínez and Álvarez35] to design a dynamic continuous controller for a mechanical system with dry friction. In ref. [Reference Cornejo and Alvarez-Icaza36], the internal states of a LuGre friction model are included as generalized coordinates in a Hamiltonian formulation for the complete mechanical system. In ref. [Reference Markus, Agee and Jimoh37], an approach that utilizes differential flatness and feedback for controlling a conventional
![]() $2$
-DOF robot arm with two actuated joints with friction was presented.
$2$
-DOF robot arm with two actuated joints with friction was presented.
1.2. Contributions of the paper
This paper deals with point-to-point control of planar
![]() $n$
-DOF robots with
$n$
-DOF robots with
![]() $n-1$
actuated joints plus one final passive joint with stiffness and viscous friction properties. An open-loop control strategy based on motor torque calculation is adopted. The focus is on oscillation suppression at the endpoint, since in many applications residual oscillations of the end-effector position may cause collisions or may lead to a longer task time to wait for the rest position of the end-effector. If under-actuated robots satisfy the differential flatness conditions, the equations of motion have a particular structure, and the last equations are linear. Hence, the last motor torque depends linearly on the flat variable. The paper exploits this property to derive an explicit expression of the robot motor torques in the presence of viscous friction; by applying such torques to the robot, oscillation-free point-to-point motions are obtained. The main contributions of the paper are as follows:
$n-1$
actuated joints plus one final passive joint with stiffness and viscous friction properties. An open-loop control strategy based on motor torque calculation is adopted. The focus is on oscillation suppression at the endpoint, since in many applications residual oscillations of the end-effector position may cause collisions or may lead to a longer task time to wait for the rest position of the end-effector. If under-actuated robots satisfy the differential flatness conditions, the equations of motion have a particular structure, and the last equations are linear. Hence, the last motor torque depends linearly on the flat variable. The paper exploits this property to derive an explicit expression of the robot motor torques in the presence of viscous friction; by applying such torques to the robot, oscillation-free point-to-point motions are obtained. The main contributions of the paper are as follows:
-
The calculation of the last motor torque in the presence of viscous friction on the passive joint, adopting a Laplace transform method. The torques of the other motors are calculated with the Newton-Euler method and include non-linear terms.
-
The analysis of the dynamic behavior of the system in the Laplace domain, that shows why an open-loop control taking into account joint friction avoids oscillations of the last link.
-
The experimental and numerical demonstration of the effectiveness of the inclusion of viscous friction in the calculation of the motor torques.
The paper is organized as follows. Section 2 presents the general model of a
![]() $n$
-DOF robot with the last non-actuated joint having stiffness and viscous friction properties. The analysis of under-actuated robots in the Laplace domain is presented in Section 3. Experimental and numerical results for a
$n$
-DOF robot with the last non-actuated joint having stiffness and viscous friction properties. The analysis of under-actuated robots in the Laplace domain is presented in Section 3. Experimental and numerical results for a
![]() $2$
-DOF robot are presented in Section 4. The model is employed to simulate a
$2$
-DOF robot are presented in Section 4. The model is employed to simulate a
![]() $4$
-DOF robot in Section 5. Finally, in Section 6 conclusions are drawn.
$4$
-DOF robot in Section 5. Finally, in Section 6 conclusions are drawn.
2. Mathematical model of the under-actuated robot
The robots studied in this paper are designed according to the theory of the differentially flat system [Reference Franch, Agrawal and Sangwan23]. A robot must satisfy certain criteria to be differentially flat. Specifically, in the case of an
![]() $n$
-DOF robot, the following conditions must be met:
$n$
-DOF robot, the following conditions must be met:
-
the center of mass of the final link (
 $n$
) must be positioned along the
$n$
) must be positioned along the
 $n$
-th joint axis;
$n$
-th joint axis; -
the center of mass of both links
 $n$
and
$n$
and
 $n-1$
must be located along the
$n-1$
must be located along the
 $(n-1)$
-th joint axis.
$(n-1)$
-th joint axis.
These conditions are iteratively applied until the center of mass of the final
![]() $j$
links (i.e.,
$j$
links (i.e.,
![]() $n, n-1, \ldots, n-j+1$
) is positioned on the
$n, n-1, \ldots, n-j+1$
) is positioned on the
![]() $(n-j+1)$
-th joint axis, as described in ref. [Reference Franch, Agrawal and Sangwan23]. As a result, the last
$(n-j+1)$
-th joint axis, as described in ref. [Reference Franch, Agrawal and Sangwan23]. As a result, the last
![]() $j$
links are called “fully balanced.” The actuators for the system are located on the
$j$
links are called “fully balanced.” The actuators for the system are located on the
![]() $(n-j+1)$
-th joint, while the
$(n-j+1)$
-th joint, while the
![]() $(j-1)$
preceding joints are equipped with torsional springs. In this paper, only one non-actuated joint is considered, hence
$(j-1)$
preceding joints are equipped with torsional springs. In this paper, only one non-actuated joint is considered, hence
![]() $j=2$
. Therefore, it is necessary to balance the robot up to the
$j=2$
. Therefore, it is necessary to balance the robot up to the
![]() $n-j+1 = n-1$
joint. Fig. 1 shows the scheme of an
$n-j+1 = n-1$
joint. Fig. 1 shows the scheme of an
![]() $n$
-DOF robot with the last passive joint.
$n$
-DOF robot with the last passive joint.
![]() $q_1$
represents the rotation of link 1 with respect to the base frame
$q_1$
represents the rotation of link 1 with respect to the base frame
![]() $x-y$
, and
$x-y$
, and
![]() $q_i$
is the relative rotation of link
$q_i$
is the relative rotation of link
![]() $i$
with respect to
$i$
with respect to
![]() $i-1$
link, with
$i-1$
link, with
![]() $i = 2,3,\dots, n$
. Only the last joint is not actuated, and the last link
$i = 2,3,\dots, n$
. Only the last joint is not actuated, and the last link
![]() $n$
is connected with link
$n$
is connected with link
![]() $n-1$
by a torsional spring with stiffness
$n-1$
by a torsional spring with stiffness
![]() $k_n$
, and by a viscous damper with damping coefficient
$k_n$
, and by a viscous damper with damping coefficient
![]() $c_n$
.
$c_n$
.

Figure 1. Scheme of the mechanical system with
![]() $n-$
DOF.
$n-$
DOF.
Coming to mass distribution, the term
![]() $m_k$
is the mass of the
$m_k$
is the mass of the
![]() $k$
-th link,
$k$
-th link,
![]() $I_{Gk}$
is the barycentric moment of inertia of the
$I_{Gk}$
is the barycentric moment of inertia of the
![]() $k$
-th element,
$k$
-th element,
![]() $a_{Gk}$
is the distance of the center of mass of
$a_{Gk}$
is the distance of the center of mass of
![]() $k$
-th link from the
$k$
-th link from the
![]() $k$
-th joint and
$k$
-th joint and
![]() $a_k$
is the total length of the
$a_k$
is the total length of the
![]() $k$
-th links (with
$k$
-th links (with
![]() $k = 1,2,\dots, n$
). Regarding the last
$k = 1,2,\dots, n$
). Regarding the last
![]() $n-1$
and
$n-1$
and
![]() $n$
balanced links,
$n$
balanced links,
![]() $m_{c(n-1)}$
and
$m_{c(n-1)}$
and
![]() $m_{c(n)}$
are the counterbalancing masses of
$m_{c(n)}$
are the counterbalancing masses of
![]() $n-1$
and
$n-1$
and
![]() $n$
links, respectively. Similarly,
$n$
links, respectively. Similarly,
![]() $a_{C(n-1)}$
and
$a_{C(n-1)}$
and
![]() $a_{C(n)}$
are the distances of the counterbalancing masses from the
$a_{C(n)}$
are the distances of the counterbalancing masses from the
![]() $n-1$
and
$n-1$
and
![]() $n$
joint axis, respectively.
$n$
joint axis, respectively.
The dynamic model of the system can be derived by means of the Lagrangian approach, the result is a system of equations that can be written in matrix form:
 \begin{equation} \boldsymbol{M}_n(\boldsymbol{q}) \begin{bmatrix} \ddot{q}_1 \\[5pt] \ddot{q}_2 \\[5pt] \vdots \\[5pt] \ddot{q}_{n-2}\\[5pt] \ddot{q}_{n-1}\\[5pt] \ddot{q}_{n}\\[5pt] \end{bmatrix} + \boldsymbol{C}_n \begin{bmatrix} \dot{q}_1 \\[5pt] \dot{q}_2 \\[5pt] \vdots \\[5pt] \dot{q}_{n-2}\\[5pt] \dot{q}_{n-1}\\[5pt] \dot{q}_{n}\\[5pt] \end{bmatrix} + \boldsymbol{K}_n \begin{bmatrix} q_1 \\[5pt] q_2\\[5pt] \vdots \\[5pt] q_{n-2}\\[5pt] q_{n-1}\\[5pt] q_n \end{bmatrix} + \begin{bmatrix} b_1(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] b_2(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] \vdots \\[5pt] b_{n-2}(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] 0\\[5pt] 0 \end{bmatrix}+ \begin{bmatrix} g_1(\boldsymbol{q}) \\[5pt] g_2(\boldsymbol{q}) \\[5pt] \vdots \\[5pt] g_{n-2}(\boldsymbol{q}) \\[5pt] 0\\[5pt] 0 \end{bmatrix} = \begin{bmatrix} \tau _1 \\[5pt] \tau _2 \\[5pt] \vdots \\[5pt] \tau _{n-2}\\[5pt] \tau _{n-1}\\[5pt] 0 \end{bmatrix} \end{equation}
\begin{equation} \boldsymbol{M}_n(\boldsymbol{q}) \begin{bmatrix} \ddot{q}_1 \\[5pt] \ddot{q}_2 \\[5pt] \vdots \\[5pt] \ddot{q}_{n-2}\\[5pt] \ddot{q}_{n-1}\\[5pt] \ddot{q}_{n}\\[5pt] \end{bmatrix} + \boldsymbol{C}_n \begin{bmatrix} \dot{q}_1 \\[5pt] \dot{q}_2 \\[5pt] \vdots \\[5pt] \dot{q}_{n-2}\\[5pt] \dot{q}_{n-1}\\[5pt] \dot{q}_{n}\\[5pt] \end{bmatrix} + \boldsymbol{K}_n \begin{bmatrix} q_1 \\[5pt] q_2\\[5pt] \vdots \\[5pt] q_{n-2}\\[5pt] q_{n-1}\\[5pt] q_n \end{bmatrix} + \begin{bmatrix} b_1(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] b_2(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] \vdots \\[5pt] b_{n-2}(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] 0\\[5pt] 0 \end{bmatrix}+ \begin{bmatrix} g_1(\boldsymbol{q}) \\[5pt] g_2(\boldsymbol{q}) \\[5pt] \vdots \\[5pt] g_{n-2}(\boldsymbol{q}) \\[5pt] 0\\[5pt] 0 \end{bmatrix} = \begin{bmatrix} \tau _1 \\[5pt] \tau _2 \\[5pt] \vdots \\[5pt] \tau _{n-2}\\[5pt] \tau _{n-1}\\[5pt] 0 \end{bmatrix} \end{equation}
in which the vector
![]() $ \boldsymbol{b}(\boldsymbol{q},\dot{\boldsymbol{q}}) = [b_1(\boldsymbol{q},\dot{\boldsymbol{q}}),b_2(\boldsymbol{q},\dot{\boldsymbol{q}}) \dots b_{n-2}(\boldsymbol{q},\dot{\boldsymbol{q}}),0,0]^T$
contains the Coriolis-centrifugal terms, while
$ \boldsymbol{b}(\boldsymbol{q},\dot{\boldsymbol{q}}) = [b_1(\boldsymbol{q},\dot{\boldsymbol{q}}),b_2(\boldsymbol{q},\dot{\boldsymbol{q}}) \dots b_{n-2}(\boldsymbol{q},\dot{\boldsymbol{q}}),0,0]^T$
contains the Coriolis-centrifugal terms, while
![]() $ \boldsymbol{g}(\boldsymbol{q}) = [g_1(\boldsymbol{q}),g_2(\boldsymbol{q}) \dots g_{n-2}(\boldsymbol{q}),0,0]^T$
is the vector of gravity terms. It is worth noting that the last two elements of the vectors are null since the last
$ \boldsymbol{g}(\boldsymbol{q}) = [g_1(\boldsymbol{q}),g_2(\boldsymbol{q}) \dots g_{n-2}(\boldsymbol{q}),0,0]^T$
is the vector of gravity terms. It is worth noting that the last two elements of the vectors are null since the last
![]() $[n-1,n]$
links are fully balanced.
$[n-1,n]$
links are fully balanced.
![]() $\tau _i$
is the motor torque applied on
$\tau _i$
is the motor torque applied on
![]() $i-$
th motor (with
$i-$
th motor (with
![]() $i=1,2,\dots, n-1$
). All the actuated joints are considered to be infinitely stiff and frictionless. Mass matrix
$i=1,2,\dots, n-1$
). All the actuated joints are considered to be infinitely stiff and frictionless. Mass matrix
![]() $\boldsymbol{M}_n$
, damping matrix
$\boldsymbol{M}_n$
, damping matrix
![]() $\boldsymbol{C}_n$
, and stiffness matrix
$\boldsymbol{C}_n$
, and stiffness matrix
![]() $\boldsymbol{K}_n$
are defined as follows:
$\boldsymbol{K}_n$
are defined as follows:
 \begin{equation} \boldsymbol{M}_n (\boldsymbol{q}) = \left [ \begin{array}{c@{\quad}c@{\quad}c} & I_{n-1}^* & I_{n}^* \\[5pt] & I_{n-1}^* & I_{n}^* \\[5pt] \boldsymbol{I}^*_{(n-2)\times (n-2)}(\boldsymbol{q}) & \vdots & \vdots \\[5pt] & I_{n-1}^* & I_{n}^* \\[5pt] I_{n-1}^* \;\;\; \cdots \;\;\; I_{n-1}^* & I_{n-1}^* & I_{n}^*\\[5pt] I_{n}^* \;\;\; \cdots \;\;\; I_{n}^* & I_{n}^* & I_{n}^*\\[5pt] \end{array} \right ], \boldsymbol{C}_n = \left [ \begin{array}{c@{\quad}c} & 0 \\[5pt] \textbf{0}_{(n-1)\times (n-1)} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\;\; \cdots \;\;\; 0 & c_n \end{array} \right ], \boldsymbol{K}_n = \left [ \begin{array}{c@{\quad}c} & 0 \\[5pt] \textbf{0}_{(n-1)\times (n-1)} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\;\; \cdots \;\;\; 0 & k_n \end{array} \right ] \end{equation}
\begin{equation} \boldsymbol{M}_n (\boldsymbol{q}) = \left [ \begin{array}{c@{\quad}c@{\quad}c} & I_{n-1}^* & I_{n}^* \\[5pt] & I_{n-1}^* & I_{n}^* \\[5pt] \boldsymbol{I}^*_{(n-2)\times (n-2)}(\boldsymbol{q}) & \vdots & \vdots \\[5pt] & I_{n-1}^* & I_{n}^* \\[5pt] I_{n-1}^* \;\;\; \cdots \;\;\; I_{n-1}^* & I_{n-1}^* & I_{n}^*\\[5pt] I_{n}^* \;\;\; \cdots \;\;\; I_{n}^* & I_{n}^* & I_{n}^*\\[5pt] \end{array} \right ], \boldsymbol{C}_n = \left [ \begin{array}{c@{\quad}c} & 0 \\[5pt] \textbf{0}_{(n-1)\times (n-1)} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\;\; \cdots \;\;\; 0 & c_n \end{array} \right ], \boldsymbol{K}_n = \left [ \begin{array}{c@{\quad}c} & 0 \\[5pt] \textbf{0}_{(n-1)\times (n-1)} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\;\; \cdots \;\;\; 0 & k_n \end{array} \right ] \end{equation}
In Eq. (2),
![]() $\textbf{0}_{(n-1)\times (n-1)}$
is the zero matrix with dimension
$\textbf{0}_{(n-1)\times (n-1)}$
is the zero matrix with dimension
![]() $n-1$
. Since the last
$n-1$
. Since the last
![]() $[n-1,n]$
links are fully balanced, the mass matrix of the system includes a
$[n-1,n]$
links are fully balanced, the mass matrix of the system includes a
![]() $(n-2)\times (n-2)$
configuration-dependent sub-matrix, two constant rows and two constant columns. The constant columns are the transpose of the rows.
$(n-2)\times (n-2)$
configuration-dependent sub-matrix, two constant rows and two constant columns. The constant columns are the transpose of the rows.
From Eq. (1), differential flatness can be used to define a set of flat variables [Reference Agrawal and Sangwan1]. For a
![]() $n$
-DOF system with one non-actuated joint, the vector of flat variables
$n$
-DOF system with one non-actuated joint, the vector of flat variables
![]() $\boldsymbol{Y} = [y_1,\ldots,y_{n-1}]$
can be defined as:
$\boldsymbol{Y} = [y_1,\ldots,y_{n-1}]$
can be defined as:
 \begin{equation} \begin{gathered} y_1 = \sum _{i=1}^n q_i\\[5pt] y_{i} = q_{i-1}\quad \text{with} \quad i = 2,3,\dots,n-1 \end{gathered} \end{equation}
\begin{equation} \begin{gathered} y_1 = \sum _{i=1}^n q_i\\[5pt] y_{i} = q_{i-1}\quad \text{with} \quad i = 2,3,\dots,n-1 \end{gathered} \end{equation}
for example,
![]() $n=4$
,
$n=4$
,
![]() $\boldsymbol{Y} = [q_1+q_2+q_3+q_4,q_1,q_2]$
. It is worth noting that flat variable
$\boldsymbol{Y} = [q_1+q_2+q_3+q_4,q_1,q_2]$
. It is worth noting that flat variable
![]() $y_1$
has the physical meaning of orientation of the last link with respect to the fixed reference frame.
$y_1$
has the physical meaning of orientation of the last link with respect to the fixed reference frame.
Flat variables can be used to control point-to-point motions of under-actuated systems and depend on the constraints on the joint values (position and derivatives) and on the total motion time
![]() $t_f$
. Although
$t_f$
. Although
![]() $\boldsymbol{Y}$
can be defined by means of any function, in most cases, polynomials are used [Reference Biagiotti and Melchiorri38]. In order to achieve the full controllability of the system, it is necessary to express all torques as a function of flat variables
$\boldsymbol{Y}$
can be defined by means of any function, in most cases, polynomials are used [Reference Biagiotti and Melchiorri38]. In order to achieve the full controllability of the system, it is necessary to express all torques as a function of flat variables
![]() $\boldsymbol{Y}$
.
$\boldsymbol{Y}$
.
If
![]() $c_n$
is equal to zero, starting from the last
$c_n$
is equal to zero, starting from the last
![]() $[n-1,n]$
rows of Eq. (1), it is possible to derive the angular position
$[n-1,n]$
rows of Eq. (1), it is possible to derive the angular position
![]() $q_n$
of the non-actuated joint as a function of the first flat variable:
$q_n$
of the non-actuated joint as a function of the first flat variable:
The motor torque applied to the
![]() $n-1$
joint can be calculated from the
$n-1$
joint can be calculated from the
![]() $n-1$
row of Eq. (1) and using Eq. (4). It results:
$n-1$
row of Eq. (1) and using Eq. (4). It results:
Since
![]() $I_n^*$
and
$I_n^*$
and
![]() $I_{n-1}^*$
are constant,
$I_{n-1}^*$
are constant,
![]() $\tau _{n-1}$
is a linear function of the derivatives of
$\tau _{n-1}$
is a linear function of the derivatives of
![]() $y_1$
. The other motor torques can be calculated starting from
$y_1$
. The other motor torques can be calculated starting from
![]() $\tau _{(n-1)}$
by means of the Newton-Euler formula [Reference Sciavicco and Siciliano39]:Footnote 1
$\tau _{(n-1)}$
by means of the Newton-Euler formula [Reference Sciavicco and Siciliano39]:Footnote 1
with
![]() $i=1,2,\dots n-2$
. The flat variable
$i=1,2,\dots n-2$
. The flat variable
![]() ${y}_{k+1}$
has the subscript
${y}_{k+1}$
has the subscript
![]() $k+1$
because the first flat variable is defined as the sum of all angular positions of the robot. Owing to the presence of the Coriolis-centrifugal terms, the gravity terms, and the configuration-dependent inertial terms, these motor torques are non-linear functions of flat variables.
$k+1$
because the first flat variable is defined as the sum of all angular positions of the robot. Owing to the presence of the Coriolis-centrifugal terms, the gravity terms, and the configuration-dependent inertial terms, these motor torques are non-linear functions of flat variables.
Only under the hypothesis of a frictionless non-actuated joint, Equation (4) can be obtained. If
![]() $c_n \neq 0$
, the analytical expression of
$c_n \neq 0$
, the analytical expression of
![]() $q_n$
as a function of only
$q_n$
as a function of only
![]() $y_1$
is difficult to obtain. In the next section, an analytical method in the Laplace domain to express the joint variable
$y_1$
is difficult to obtain. In the next section, an analytical method in the Laplace domain to express the joint variable
![]() $q_n$
as a function of a flat variable in the presence of viscous friction is presented.
$q_n$
as a function of a flat variable in the presence of viscous friction is presented.
3. Laplace domain analysis of the last two motion equations
The last two rows of Eq. (1) are linear since the last
![]() $[n-1,n]$
links satisfy the differential flatness rules and are fully balanced. Hence, the Laplace transform can be rigorously calculated.
$[n-1,n]$
links satisfy the differential flatness rules and are fully balanced. Hence, the Laplace transform can be rigorously calculated.
3.1. Motor torque calculation in the presence of viscous damping
The flat variable
![]() $y_1 = \sum _{i=1}^n q_i$
with
$y_1 = \sum _{i=1}^n q_i$
with
![]() $i=1,2,\dots,n$
, and its derivatives can be written in the Laplace domain as follows:
$i=1,2,\dots,n$
, and its derivatives can be written in the Laplace domain as follows:
 \begin{equation} \begin{aligned} \mathcal{L}(y_1 (t))& = Y_1(s) = \sum _{i=1}^n Q_i(s) \\[5pt] \mathcal{L}(\dot{y}_1(t))& = s Y_1(s) =s \sum _{i=1}^n Q_i(s)\\[5pt] \mathcal{L}(\ddot{y}_1(t))& = s^2 Y_1(s) = s^2 \sum _{i=1}^n Q_i(s) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \mathcal{L}(y_1 (t))& = Y_1(s) = \sum _{i=1}^n Q_i(s) \\[5pt] \mathcal{L}(\dot{y}_1(t))& = s Y_1(s) =s \sum _{i=1}^n Q_i(s)\\[5pt] \mathcal{L}(\ddot{y}_1(t))& = s^2 Y_1(s) = s^2 \sum _{i=1}^n Q_i(s) \end{aligned} \end{equation}
in which
![]() $\mathcal{L}$
means Laplace transform.
$\mathcal{L}$
means Laplace transform.
The last two equations of motion considering the damping coefficient
![]() $c_n\neq 0$
can be rewritten as follows:
$c_n\neq 0$
can be rewritten as follows:
 \begin{equation} \begin{cases} I_{n-1}^*s^2(Y_1(s)-Q_n(s))+ I_n^* s^2Q_n(s) = T_{n-1}(s)\\[5pt] I_{n}^*s^2Y_1(s)+(c_n s+k_n)Q_n(s) = 0\\[5pt] \end{cases} \end{equation}
\begin{equation} \begin{cases} I_{n-1}^*s^2(Y_1(s)-Q_n(s))+ I_n^* s^2Q_n(s) = T_{n-1}(s)\\[5pt] I_{n}^*s^2Y_1(s)+(c_n s+k_n)Q_n(s) = 0\\[5pt] \end{cases} \end{equation}
in which
![]() $T_{n-1}(s)$
is the motor torque of the last non-actuated joint. The joint variable
$T_{n-1}(s)$
is the motor torque of the last non-actuated joint. The joint variable
![]() $Q_n(s)$
can be obtained from the last row of Eq. (8):
$Q_n(s)$
can be obtained from the last row of Eq. (8):
The torque that the last actuated joint has to generate can be obtained from the first row of Eq. (8) introducing Eq. (9):
in which
![]() $\tilde{T}_{(n-1)}(s)$
is the motor torque that takes into account the damping coefficient and
$\tilde{T}_{(n-1)}(s)$
is the motor torque that takes into account the damping coefficient and
![]() $\tilde{k}_n = k_n+sc_n$
is the complex stiffness of the non-actuated joint.
$\tilde{k}_n = k_n+sc_n$
is the complex stiffness of the non-actuated joint.
Equation (10) can be rewritten collecting the stiffness
![]() $k_n$
from the second term, it results:
$k_n$
from the second term, it results:
Usually, the damping coefficient
![]() $c_n$
is much smaller than torsion spring stiffness, especially if low-friction bearings are used. For this reason, the term
$c_n$
is much smaller than torsion spring stiffness, especially if low-friction bearings are used. For this reason, the term
![]() $(1+c_n/k_n\,s)^{-1}$
can be approximated using its Taylor expansion arrested at the first order. Hence, Eq. (11) can be written as follows:
$(1+c_n/k_n\,s)^{-1}$
can be approximated using its Taylor expansion arrested at the first order. Hence, Eq. (11) can be written as follows:
Hence, the expression of the motor torque
![]() $\tilde{T}_{n-1}$
in the Laplace domain takes the final form:
$\tilde{T}_{n-1}$
in the Laplace domain takes the final form:
Finally, it is possible to express motor torque
![]() $\tilde{T}_{n-1}(s)$
in the time domain by means of the inverse Laplace transform (the initial condition are zero):
$\tilde{T}_{n-1}(s)$
in the time domain by means of the inverse Laplace transform (the initial condition are zero):
It is worth noting that the introduction of viscous friction leads to an increase in the order of the derivative of the flat variable that appears in the expression of the motor torque. Hence, the degree of the polynomial representing
![]() $y_1$
must increase to satisfy constraints on the fifth derivative. Equation (6) is still valid if the damped motor torque
$y_1$
must increase to satisfy constraints on the fifth derivative. Equation (6) is still valid if the damped motor torque
![]() $\tilde{\tau }_{n-1}$
is used instead of
$\tilde{\tau }_{n-1}$
is used instead of
![]() $\tau _{n-1}$
:
$\tau _{n-1}$
:
with
![]() $i=1,2,\dots n-2$
.
$i=1,2,\dots n-2$
.
3.2. Natural frequencies
Free vibrations analysis makes it possible to identify the resonances of the system and is preliminary to forced vibrations analysis.
In the actual operation of the robot, the sum of the joint variables is an output that depends on the motor torques which are functions of the commanded flat variables. Hence, in the analysis of natural frequencies and forced response, the sum of joint variables in the Laplace domain is named
![]() $\Theta _n(s)$
.
$\Theta _n(s)$
.
The last equations of motion considering the damping coefficient (
![]() $c_n\neq 0$
) can be rewritten as follows in the Laplace domain:
$c_n\neq 0$
) can be rewritten as follows in the Laplace domain:
 \begin{equation} \begin{cases} s^2 I_{n-1}^*(\Theta _n(s)-Q_n(s))+s^2 I_n^* Q_n(s) = T_{n-1}(s)\\[5pt] s^2 I_{n}^*\Theta _n(s)+(c_n s+k_n)Q_n(s) = 0\\[5pt] \end{cases} \end{equation}
\begin{equation} \begin{cases} s^2 I_{n-1}^*(\Theta _n(s)-Q_n(s))+s^2 I_n^* Q_n(s) = T_{n-1}(s)\\[5pt] s^2 I_{n}^*\Theta _n(s)+(c_n s+k_n)Q_n(s) = 0\\[5pt] \end{cases} \end{equation}
in which
![]() $T_{n-1}(s)$
is the motor torque for the last non-actuated joint.
$T_{n-1}(s)$
is the motor torque for the last non-actuated joint.
If the motor torque
![]() $T_{n-1}(s)$
and
$T_{n-1}(s)$
and
![]() $c_n$
are set to zero, the equations of free undamped vibrations are obtained. The natural frequencies of the undamped system can be determined by finding the roots of the determinant of the matrix that multiplies the vector of unknowns:
$c_n$
are set to zero, the equations of free undamped vibrations are obtained. The natural frequencies of the undamped system can be determined by finding the roots of the determinant of the matrix that multiplies the vector of unknowns:
 \begin{equation} \begin{bmatrix} I_{n-1}^*s^2 & (I_{n}^*-I_{n-1}^*)s^2 \\[5pt] I_{n}^*s^2 & k_n \\[5pt] \end{bmatrix} \begin{bmatrix} \Theta _1(s)\\[5pt] Q_{n}(s) \end{bmatrix} = \begin{bmatrix} 0\\[5pt] 0 \end{bmatrix} \end{equation}
\begin{equation} \begin{bmatrix} I_{n-1}^*s^2 & (I_{n}^*-I_{n-1}^*)s^2 \\[5pt] I_{n}^*s^2 & k_n \\[5pt] \end{bmatrix} \begin{bmatrix} \Theta _1(s)\\[5pt] Q_{n}(s) \end{bmatrix} = \begin{bmatrix} 0\\[5pt] 0 \end{bmatrix} \end{equation}
The determinant of the matrix at the left-hand side of Eq. (17) is:
Equation (18) shows that one solution is null since it corresponds to a rigid motion of the system. The other non-null solution is the natural frequency of the system:
 \begin{equation} \omega _n = \sqrt{\frac{k_n I_{n-1}^*}{I_{n}^*(I_{n-1}^*-I_{n}^*)}} \end{equation}
\begin{equation} \omega _n = \sqrt{\frac{k_n I_{n-1}^*}{I_{n}^*(I_{n-1}^*-I_{n}^*)}} \end{equation}
3.3. Forced vibrations
Coming back to Eq. (16), the transfer function of the system between the joint variable
![]() $Q_n(s)$
and the generic input
$Q_n(s)$
and the generic input
![]() $T_{n-1}(s)$
can be calculated as follows:
$T_{n-1}(s)$
can be calculated as follows:
Since Eq. (20) shows that the transfer function
![]() $Q_n(s)/T_{n-1}(s)$
has a pair of complex conjugate poles, in general, the response is characterized by damped oscillations.
$Q_n(s)/T_{n-1}(s)$
has a pair of complex conjugate poles, in general, the response is characterized by damped oscillations.
If the particular torque input, calculated with the flat variable (Eq. (10)), is considered:
when Eq. (21) is introduced in Eq. (20), a zero-pole cancelation takes place:
which corresponds to the disappearance of the oscillations.
Conversely, if the torque input is calculated by setting the damping coefficient
![]() $c_n$
equal to
$c_n$
equal to
![]() $0$
, Eq. (10) takes the following form:
$0$
, Eq. (10) takes the following form:
When this torque is introduced in Eq. (20), the zero-pole cancelation does not take place, and owing to the complex conjugate poles oscillations may occur:
4. Numerical and experimental results for a
 $2$
-DOF robot
$2$
-DOF robot
The robot designed for the experimental validation of the mathematical model has
![]() $2$
-DOF (
$2$
-DOF (
![]() $n=2$
), with one motor and one non-actuated joint. It moves on the horizontal plane, and link 2 is fully balanced. The first link does not need to be balanced, since its moment of inertia about joint
$n=2$
), with one motor and one non-actuated joint. It moves on the horizontal plane, and link 2 is fully balanced. The first link does not need to be balanced, since its moment of inertia about joint
![]() $1$
is always constant [Reference Agrawal and Sangwan1].
$1$
is always constant [Reference Agrawal and Sangwan1].
For such a robot, Eq. (1) takes the following form:
 \begin{equation} \boldsymbol{M}_2 \begin{bmatrix} \ddot{q}_1 \\[5pt] \ddot{q}_2 \end{bmatrix} + \boldsymbol{C}_2 \begin{bmatrix} \dot{q}_1 \\[5pt] \dot{q}_2 \end{bmatrix} + \boldsymbol{K}_2 \begin{bmatrix} q_1 \\[5pt] q_2 \end{bmatrix} = \begin{bmatrix} \tau _1 \\[5pt] 0 \end{bmatrix} \end{equation}
\begin{equation} \boldsymbol{M}_2 \begin{bmatrix} \ddot{q}_1 \\[5pt] \ddot{q}_2 \end{bmatrix} + \boldsymbol{C}_2 \begin{bmatrix} \dot{q}_1 \\[5pt] \dot{q}_2 \end{bmatrix} + \boldsymbol{K}_2 \begin{bmatrix} q_1 \\[5pt] q_2 \end{bmatrix} = \begin{bmatrix} \tau _1 \\[5pt] 0 \end{bmatrix} \end{equation}
where
![]() $\tau _1$
is the motor torque and the matrices are defined as follows:
$\tau _1$
is the motor torque and the matrices are defined as follows:
 \begin{equation} \boldsymbol{M}_2 = \begin{bmatrix} I_1^* & I_2^* \\[5pt] I_2^* & I_2^* \\[5pt] \end{bmatrix}, \boldsymbol{C}_2 = \begin{bmatrix} 0 & 0 \\[5pt] 0 & c_2 \\[5pt] \end{bmatrix}, \boldsymbol{K}_2 = \begin{bmatrix} 0 & 0 \\[5pt] 0 & k_2 \\[5pt] \end{bmatrix} \end{equation}
\begin{equation} \boldsymbol{M}_2 = \begin{bmatrix} I_1^* & I_2^* \\[5pt] I_2^* & I_2^* \\[5pt] \end{bmatrix}, \boldsymbol{C}_2 = \begin{bmatrix} 0 & 0 \\[5pt] 0 & c_2 \\[5pt] \end{bmatrix}, \boldsymbol{K}_2 = \begin{bmatrix} 0 & 0 \\[5pt] 0 & k_2 \\[5pt] \end{bmatrix} \end{equation}
in which the moments of inertia are
![]() $I_1^* = I_{G1} + m_1 a_{G1}^2 + (m_2+m_{c2}) a_{1}^2 + I_{G2}+m_2a_{G2}^2+m_{c2}a_{c2}^2$
, and
$I_1^* = I_{G1} + m_1 a_{G1}^2 + (m_2+m_{c2}) a_{1}^2 + I_{G2}+m_2a_{G2}^2+m_{c2}a_{c2}^2$
, and
![]() $I_2^* = I_{G2}+m_2a_{G2}^2+m_{c2}a_{c2}^2$
, and
$I_2^* = I_{G2}+m_2a_{G2}^2+m_{c2}a_{c2}^2$
, and
![]() $c_2$
is the damping coefficient of the second joint. It is worth noting that, in this case, the mass matrix is constant and the Coriolis-centrifugal and gravity terms are null because the second link is balanced and the system works in the horizontal plane.
$c_2$
is the damping coefficient of the second joint. It is worth noting that, in this case, the mass matrix is constant and the Coriolis-centrifugal and gravity terms are null because the second link is balanced and the system works in the horizontal plane.
Only one flat variable is required:
![]() $y_1=q_1+q_2$
. If
$y_1=q_1+q_2$
. If
![]() $c_2 = 0$
, the motor torque of the first joint is calculated by means of Eq. (5):
$c_2 = 0$
, the motor torque of the first joint is calculated by means of Eq. (5):
whereas the motor torque for the damped systems is calculated by means of Eq. (14):
The flat variable is chosen to obtain a specific position, velocity, acceleration, jerk, and snap of
![]() $q_1$
and
$q_1$
and
![]() $q_2$
at the beginning and at the end of the motion (
$q_2$
at the beginning and at the end of the motion (
![]() $t_f$
). For the undamped system, a
$t_f$
). For the undamped system, a
![]() $9$
-th degree polynomial is sufficient, and the corresponding constraints on the flat variable
$9$
-th degree polynomial is sufficient, and the corresponding constraints on the flat variable
![]() $y_1$
are as follows:
$y_1$
are as follows:
 \begin{equation} \begin{cases} y_1(t_i) = q_{1i}+q_{2i}\\[5pt] y_1(t_f) = q_{1f}+q_{2f} \\[5pt] \dot{y}_1(t_i) = \ddot{y}_1(t_i) = y_1^{(3)}(t_i) = y_1^{(4)}(t_i) = 0\\[5pt] \dot{y}_1(t_f) = \ddot{y}_1(t_f) = y_1^{(3)}(t_f) = y_1^{(4)}(t_f) = 0 \end{cases} \end{equation}
\begin{equation} \begin{cases} y_1(t_i) = q_{1i}+q_{2i}\\[5pt] y_1(t_f) = q_{1f}+q_{2f} \\[5pt] \dot{y}_1(t_i) = \ddot{y}_1(t_i) = y_1^{(3)}(t_i) = y_1^{(4)}(t_i) = 0\\[5pt] \dot{y}_1(t_f) = \ddot{y}_1(t_f) = y_1^{(3)}(t_f) = y_1^{(4)}(t_f) = 0 \end{cases} \end{equation}
where
![]() $q_{1i}$
,
$q_{1i}$
,
![]() $q_{1f}$
,
$q_{1f}$
,
![]() $q_{2i}$
, and
$q_{2i}$
, and
![]() $q_{2f}$
are the initial and final angular positions of joint 1 and joint 2, respectively. For the damped system, at least an
$q_{2f}$
are the initial and final angular positions of joint 1 and joint 2, respectively. For the damped system, at least an
![]() $11$
-th degree polynomial must be used to obtain a continuous fifth derivative
$11$
-th degree polynomial must be used to obtain a continuous fifth derivative
![]() $y_1^{(5)}$
. Hence,
$y_1^{(5)}$
. Hence,
![]() $y_1$
is defined by an
$y_1$
is defined by an
![]() $11$
-th degree polynomial, and the boundary conditions are the same as Eq. (29) with the addition of the constraints on the crackle:
$11$
-th degree polynomial, and the boundary conditions are the same as Eq. (29) with the addition of the constraints on the crackle:
 \begin{equation} \begin{cases} y^{(5)}_1(t_i) = 0\\[5pt] y^{(5)}_1(t_f) = 0 \end{cases} \end{equation}
\begin{equation} \begin{cases} y^{(5)}_1(t_i) = 0\\[5pt] y^{(5)}_1(t_f) = 0 \end{cases} \end{equation}
The constants of the polynomial are obtained by solving the linear system:
in which
![]() $\boldsymbol{A}$
is the matrix associated with the boundary conditions,
$\boldsymbol{A}$
is the matrix associated with the boundary conditions,
![]() $\boldsymbol{x}$
is the vector of the polynomial coefficients and
$\boldsymbol{x}$
is the vector of the polynomial coefficients and
![]() $\boldsymbol{b}$
is the vector that contains the boundary conditions [Reference Jazar40].
$\boldsymbol{b}$
is the vector that contains the boundary conditions [Reference Jazar40].
The prototype was built using additive manufacturing and moves in the horizontal plane as depicted in Fig. 2. The first joint is actuated by means of a direct drive Portescap 35NT2R82 426SP brushed DC motor. The non-actuated joint is equipped with a small torsional spring with a stiffness of 0.0026
![]() $Nm/rad$
identified via modal analysis directly on the prototype [Reference Tonan, Bottin, Doria and Rosati41]. The inertial properties of links 1 and 2 are summarized in Table I. It should be noted that the
$Nm/rad$
identified via modal analysis directly on the prototype [Reference Tonan, Bottin, Doria and Rosati41]. The inertial properties of links 1 and 2 are summarized in Table I. It should be noted that the
![]() $m_i$
term represents the mass of the
$m_i$
term represents the mass of the
![]() $i$
-th link without considering any balancing mass
$i$
-th link without considering any balancing mass
![]() $m_{ci}$
. The details of stiffness, damping coefficient, and the commanded point-to-point motion are listed in Table II. It is worth noting that, for a point-to-point motion, the initial and final angles of the under-actuated joint (i.e.,
$m_{ci}$
. The details of stiffness, damping coefficient, and the commanded point-to-point motion are listed in Table II. It is worth noting that, for a point-to-point motion, the initial and final angles of the under-actuated joint (i.e.,
![]() $q_{2i}$
and
$q_{2i}$
and
![]() $q_{2f}$
) must be null [Reference Bottin and Rosati26]. The damping coefficient of the under-actuated joint
$q_{2f}$
) must be null [Reference Bottin and Rosati26]. The damping coefficient of the under-actuated joint
![]() $c_2$
is identified by means of free vibration tests on the prototype using the logarithmic decrement method [Reference Kelly42]. The experimental natural frequencies of the prototype robot are
$c_2$
is identified by means of free vibration tests on the prototype using the logarithmic decrement method [Reference Kelly42]. The experimental natural frequencies of the prototype robot are
![]() $0$
and
$0$
and
![]() $1.4\,\,Hz$
. They are in good agreement with the analytical values calculated by means of the formulas of Section 3.2.
$1.4\,\,Hz$
. They are in good agreement with the analytical values calculated by means of the formulas of Section 3.2.

Figure 2. The
![]() $2$
-DOF robot used in the experimental tests. The motor of the device is located under the black plane to avoid interference with the vision system.
$2$
-DOF robot used in the experimental tests. The motor of the device is located under the black plane to avoid interference with the vision system.
The response of the prototype robot to the torques calculated by means of the standard and the improved diffeomorphism (with viscous friction) is studied both experimentally and numerically. For the experimental validation, the measurement of joint variables is needed. The angle of the actuated joint (
![]() $q_1$
) is obtained by means of an incremental optical encoder LIKA Electronic I58-L-5000ZCU16R installed on the motor of joint 1. A second encoder, for the measurement of the passive joint angle (
$q_1$
) is obtained by means of an incremental optical encoder LIKA Electronic I58-L-5000ZCU16R installed on the motor of joint 1. A second encoder, for the measurement of the passive joint angle (
![]() $q_2$
), would represent an added mass. Hence, the second link is equipped with two markers, and its trajectory is tracked by the industrial camera Dalsa Genie Nano GM30-M2050, having a resolution of
$q_2$
), would represent an added mass. Hence, the second link is equipped with two markers, and its trajectory is tracked by the industrial camera Dalsa Genie Nano GM30-M2050, having a resolution of
![]() $2064\times 1544$
pixels and using a sensor Sony IMX252.
$2064\times 1544$
pixels and using a sensor Sony IMX252.
For the simulations, the model of Eq. (25) with the parameters of Tables I and II is implemented in Simulink.
Three scenarios are studied:
-
Control based on the simple diffeomorphism (
 $c_2=0$
) with
$c_2=0$
) with
 $y_1$
represented by a
$y_1$
represented by a
 $9$
-th degree polynomial.
$9$
-th degree polynomial. -
Control based on the simple diffeomorphism (
 $c_2=0$
) with
$c_2=0$
) with
 $y_1$
represented by an
$y_1$
represented by an
 $11$
-th degree polynomial.
$11$
-th degree polynomial. -
Control based on the new diffeomorphism (
 $c_2\neq 0$
) with
$c_2\neq 0$
) with
 $y_1$
represented by an
$y_1$
represented by an
 $11$
-th degree polynomial.
$11$
-th degree polynomial.
Figs. 3 and 4 depict the simulated and measured motion when the joint 1 torque is calculated according to the simple diffeomorphism (
![]() $c_2=0$
) with a
$c_2=0$
) with a
![]() $9$
-th degree polynomial, and with an
$9$
-th degree polynomial, and with an
![]() $11$
-th degree polynomial, respectively. In both cases, there is a good agreement between numerical and experimental results. The end-effector of the robot describes a trajectory with a cusp. It is worth noting that the area swept by the robot is smaller than the area swept by a
$11$
-th degree polynomial, respectively. In both cases, there is a good agreement between numerical and experimental results. The end-effector of the robot describes a trajectory with a cusp. It is worth noting that the area swept by the robot is smaller than the area swept by a
![]() $1$
-DOF robot made by a unique link with length
$1$
-DOF robot made by a unique link with length
![]() $a_1+a_2$
. The increase in the order of the polynomial modifies the shape of the trajectory near the cusp. In both cases, the end-effector has an overshoot and before stopping oscillates around the final position. It is worth noting that the robot is not aligned to the
$a_1+a_2$
. The increase in the order of the polynomial modifies the shape of the trajectory near the cusp. In both cases, the end-effector has an overshoot and before stopping oscillates around the final position. It is worth noting that the robot is not aligned to the
![]() $x$
-axis at the end of the planned motion (
$x$
-axis at the end of the planned motion (
![]() $t=0.6\,\,s$
), since it is still oscillating.
$t=0.6\,\,s$
), since it is still oscillating.
Table I. Inertial parameters of the simulated and experimental robot.

Table II. Stiffness and damping coefficient of the non-actuated joint used in the simulated and experimental robot and the motion parameters.


Figure 3.
![]() $2$
-DOF robot trajectory of the end-effector in
$2$
-DOF robot trajectory of the end-effector in
![]() $x-y$
plane obtained with
$x-y$
plane obtained with
![]() $y_1$
described by a
$y_1$
described by a
![]() $9$
-th degree polynomial, without the viscous friction on the non-actuated joint (
$9$
-th degree polynomial, without the viscous friction on the non-actuated joint (
![]() $c_2=0$
). The black trajectory is obtained by a
$c_2=0$
). The black trajectory is obtained by a
![]() $1$
-DOF robot with only one link of length
$1$
-DOF robot with only one link of length
![]() $a_1+a_2$
.
$a_1+a_2$
.

Figure 4.
![]() $2$
-DOF robot trajectory of the end-effector in
$2$
-DOF robot trajectory of the end-effector in
![]() $x-y$
plane obtained with
$x-y$
plane obtained with
![]() $y_1$
described by an
$y_1$
described by an
![]() $11$
-th degree polynomial, without the viscous friction on the non-actuated joint (
$11$
-th degree polynomial, without the viscous friction on the non-actuated joint (
![]() $c_2=0$
). The black trajectory is obtained by a
$c_2=0$
). The black trajectory is obtained by a
![]() $1$
-DOF robot with only one link of length
$1$
-DOF robot with only one link of length
![]() $a_1+a_2$
.
$a_1+a_2$
.
Fig. 5 shows the effect of the torque calculated taking into account joint viscous friction (
![]() $c_2\neq 0$
). In this case, the overshoot and the oscillations are strongly reduced and at the end of the planned motion, the two links are aligned. The agreement between experimental and numerical results is good.
$c_2\neq 0$
). In this case, the overshoot and the oscillations are strongly reduced and at the end of the planned motion, the two links are aligned. The agreement between experimental and numerical results is good.

Figure 5.
![]() $2$
-DOF robot trajectory of the end-effector in
$2$
-DOF robot trajectory of the end-effector in
![]() $x-y$
plane obtained with
$x-y$
plane obtained with
![]() $y_1$
described by an
$y_1$
described by an
![]() $11$
-th degree polynomial, with the viscous friction on the non-actuated joint (
$11$
-th degree polynomial, with the viscous friction on the non-actuated joint (
![]() $c_2\neq 0$
). The black trajectory is obtained by a
$c_2\neq 0$
). The black trajectory is obtained by a
![]() $1$
-DOF robot with only one link of length
$1$
-DOF robot with only one link of length
![]() $a_1+a_2$
.
$a_1+a_2$
.
It is worth noticing that the shape of the trajectory changes with the polynomial degree and with the inclusion of viscous friction. End-effector trajectory is also influenced by the non-actuated joint stiffness and the motion time, as shown in ref. [Reference Tonan, Doria, Bottin and Rosati9].
To highlight the effect of the diffeomorphism on the oscillation of the robot, the simulated and measured joint variables are depicted in Fig. 6. There is a good agreement between the two sets of results. The comparison between
![]() $q_1$
and
$q_1$
and
![]() $q_2$
depicted in Fig. 6 shows that the oscillations at the end of the planned motion chiefly involve the second joint which is non-actuated. The right side of Fig. 6 shows that if the simple diffeomorphism is adopted, there are large oscillations of
$q_2$
depicted in Fig. 6 shows that the oscillations at the end of the planned motion chiefly involve the second joint which is non-actuated. The right side of Fig. 6 shows that if the simple diffeomorphism is adopted, there are large oscillations of
![]() $q_2$
whose frequency is equal to
$q_2$
whose frequency is equal to
![]() $\omega _n$
. The increase in the order of the polynomial has a small effect on the amplitude of such oscillations. Conversely, the adoption of the new diffeomorphism leads to a nearly complete disappearance of oscillations of
$\omega _n$
. The increase in the order of the polynomial has a small effect on the amplitude of such oscillations. Conversely, the adoption of the new diffeomorphism leads to a nearly complete disappearance of oscillations of
![]() $q_2$
. The suppression of oscillations at the end of the trajectory is due to the zero-pole cancelation described in Section 3.3.
$q_2$
. The suppression of oscillations at the end of the trajectory is due to the zero-pole cancelation described in Section 3.3.

Figure 6.
![]() $2$
-DOF robot numerical and experimental joint rotations (left:
$2$
-DOF robot numerical and experimental joint rotations (left:
![]() $q_1$
; right:
$q_1$
; right:
![]() $q_2$
) in the case of three different open-loop controls: frictionless control with
$q_2$
) in the case of three different open-loop controls: frictionless control with
![]() $9$
-th degree polynomial law for
$9$
-th degree polynomial law for
![]() $y_1$
(top), frictionless control with
$y_1$
(top), frictionless control with
![]() $11$
-th degree polynomial (middle), friction compensation control with
$11$
-th degree polynomial (middle), friction compensation control with
![]() $11$
-th degree polynomial (bottom).
$11$
-th degree polynomial (bottom).
5. Numerical results for a
 $4$
-DOF robot
$4$
-DOF robot
This section aims to show the application of the general theory to a more complex under-actuated robot with
![]() $4$
-DOF having non-linear terms and operating in the horizontal plane. Trajectories are simulated to highlight the effect of torques calculated with and without viscous friction. For this robot, Eq. (1) becomes:
$4$
-DOF having non-linear terms and operating in the horizontal plane. Trajectories are simulated to highlight the effect of torques calculated with and without viscous friction. For this robot, Eq. (1) becomes:
 \begin{equation} \boldsymbol{M}_4 (\boldsymbol{q}) \begin{bmatrix} \ddot{q}_1 \\[5pt] \ddot{q}_2 \\[5pt] \ddot{q}_3 \\[5pt] \ddot{q}_4 \end{bmatrix} + \boldsymbol{C}_4 \begin{bmatrix} \dot{q}_1 \\[5pt] \dot{q}_2 \\[5pt] \dot{q}_3 \\[5pt] \dot{q}_4 \end{bmatrix} + \boldsymbol{K}_4 \begin{bmatrix} q_1 \\[5pt] q_2 \\[5pt] q_3 \\[5pt] q_4 \end{bmatrix} + \begin{bmatrix} b_1(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] b_2(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] 0 \\[5pt] 0 \end{bmatrix}= \boldsymbol{\tau } \end{equation}
\begin{equation} \boldsymbol{M}_4 (\boldsymbol{q}) \begin{bmatrix} \ddot{q}_1 \\[5pt] \ddot{q}_2 \\[5pt] \ddot{q}_3 \\[5pt] \ddot{q}_4 \end{bmatrix} + \boldsymbol{C}_4 \begin{bmatrix} \dot{q}_1 \\[5pt] \dot{q}_2 \\[5pt] \dot{q}_3 \\[5pt] \dot{q}_4 \end{bmatrix} + \boldsymbol{K}_4 \begin{bmatrix} q_1 \\[5pt] q_2 \\[5pt] q_3 \\[5pt] q_4 \end{bmatrix} + \begin{bmatrix} b_1(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] b_2(\boldsymbol{q},\dot{\boldsymbol{q}}) \\[5pt] 0 \\[5pt] 0 \end{bmatrix}= \boldsymbol{\tau } \end{equation}
in which
![]() $\boldsymbol{M}_4 (\boldsymbol{q})$
,
$\boldsymbol{M}_4 (\boldsymbol{q})$
,
![]() $\boldsymbol{C}_4$
, and
$\boldsymbol{C}_4$
, and
![]() $\boldsymbol{K}_4$
are the mass, damping, and stiffness matrices, respectively. These matrices are defined as follows:
$\boldsymbol{K}_4$
are the mass, damping, and stiffness matrices, respectively. These matrices are defined as follows:
 \begin{equation} \boldsymbol{M}_4 (\boldsymbol{q}) = \begin{bmatrix} I_{11}^*(\boldsymbol{q}) & I_{12}^*(\boldsymbol{q}) & I_{3}^* & I_{4}^* \\[5pt] I_{21}^*(\boldsymbol{q}) & I_{22}^*(\boldsymbol{q}) & I_{3}^* & I_{4}^* \\[5pt] I_{3}^* & I_{3}^* & I_{3}^* & I_{4}^* \\[5pt] I_{4}^* & I_{4}^* & I_{4}^* & I_{4}^* \end{bmatrix} \boldsymbol{C}_4 = \left [ \begin{array}{cc} & 0 \\[5pt] \textbf{0}_{3\times 3} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\;\; \cdots \;\;\; 0 & c_4 \end{array} \right ], \quad \boldsymbol{K}_4 = \left [ \begin{array}{c@{\quad}c} & 0 \\[5pt] \textbf{0}_{3\times 3} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\; \cdots \;\; 0 & k_4 \end{array} \right ] \end{equation}
\begin{equation} \boldsymbol{M}_4 (\boldsymbol{q}) = \begin{bmatrix} I_{11}^*(\boldsymbol{q}) & I_{12}^*(\boldsymbol{q}) & I_{3}^* & I_{4}^* \\[5pt] I_{21}^*(\boldsymbol{q}) & I_{22}^*(\boldsymbol{q}) & I_{3}^* & I_{4}^* \\[5pt] I_{3}^* & I_{3}^* & I_{3}^* & I_{4}^* \\[5pt] I_{4}^* & I_{4}^* & I_{4}^* & I_{4}^* \end{bmatrix} \boldsymbol{C}_4 = \left [ \begin{array}{cc} & 0 \\[5pt] \textbf{0}_{3\times 3} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\;\; \cdots \;\;\; 0 & c_4 \end{array} \right ], \quad \boldsymbol{K}_4 = \left [ \begin{array}{c@{\quad}c} & 0 \\[5pt] \textbf{0}_{3\times 3} & \vdots \\[5pt] & 0 \\[5pt] 0 \;\; \cdots \;\; 0 & k_4 \end{array} \right ] \end{equation}
The elements of the mass matrix
![]() $\boldsymbol{M}_4 (\boldsymbol{q})$
and of the vector of Coriolis-centrifugal terms are rather complex and are reported in the Appendix.
$\boldsymbol{M}_4 (\boldsymbol{q})$
and of the vector of Coriolis-centrifugal terms are rather complex and are reported in the Appendix.
The vector
![]() $\boldsymbol{\tau }$
contains the motor torques of the first, second, and third actuated joints. According to Eq. (3), the three flat variables are
$\boldsymbol{\tau }$
contains the motor torques of the first, second, and third actuated joints. According to Eq. (3), the three flat variables are
![]() $\boldsymbol{Y}=[y_1,y_2,y_3] = [q_1+q_2+q_3+q_4, q_1, q_2]$
. The motor torques without considering the viscous friction can be calculated from Equations (5) and (6) imposing
$\boldsymbol{Y}=[y_1,y_2,y_3] = [q_1+q_2+q_3+q_4, q_1, q_2]$
. The motor torques without considering the viscous friction can be calculated from Equations (5) and (6) imposing
![]() $n=4$
.
$n=4$
.
 \begin{equation} \begin{gathered}{\tau }_3 = I_{3}^* \ddot{y}_1 + \frac{ I_4^*(I_{3}^*-I_4^*) }{k_4} y_1^{(4)}\\[5pt] {\tau }_2 = \left (I_{21}^*(y_3)-I_{3}^*\right ) \ddot{y}_{2}+\left (I_{22}^*(y_3)-I_{3}^*\right ) \ddot{y}_{3}+b_2(y_3,\dot{y}_2)+{\tau }_{3} \\[5pt] {\tau }_1 = \left (I_{11}^*(y_3)-I_{21}^*(y_3)\right ) \ddot{y}_{2}+\left (I_{12}^*(y_3)-I_{22}^*(y_3)\right ) \ddot{y}_{3}+\left (b_1(y_3,\dot{y}_2,\dot{y}_3)-b_2(y_3,\dot{y}_2)\right )+{\tau }_{2}\\[5pt] \end{gathered} \end{equation}
\begin{equation} \begin{gathered}{\tau }_3 = I_{3}^* \ddot{y}_1 + \frac{ I_4^*(I_{3}^*-I_4^*) }{k_4} y_1^{(4)}\\[5pt] {\tau }_2 = \left (I_{21}^*(y_3)-I_{3}^*\right ) \ddot{y}_{2}+\left (I_{22}^*(y_3)-I_{3}^*\right ) \ddot{y}_{3}+b_2(y_3,\dot{y}_2)+{\tau }_{3} \\[5pt] {\tau }_1 = \left (I_{11}^*(y_3)-I_{21}^*(y_3)\right ) \ddot{y}_{2}+\left (I_{12}^*(y_3)-I_{22}^*(y_3)\right ) \ddot{y}_{3}+\left (b_1(y_3,\dot{y}_2,\dot{y}_3)-b_2(y_3,\dot{y}_2)\right )+{\tau }_{2}\\[5pt] \end{gathered} \end{equation}
The motor torques with viscous friction can be calculated from Equations (14) and (15) imposing
![]() $n=4$
, the expressions are as follows:
$n=4$
, the expressions are as follows:
 \begin{equation} \begin{gathered} \tilde{\tau }_3 = I_{3}^* \ddot{y}_1 + \frac{ I_4^*(I_{3}^*-I_4^*) }{k_4} y_1^{(4)} - \frac{c_4 I_4^*(I_{3}^*-I_4^*)}{k_4^2} y_1^{(5)}\\[5pt] \tilde{\tau }_2 = \left (I_{21}^*(y_3)-I_{3}^*\right ) \ddot{y}_{2}+\left (I_{22}^*(y_3)-I_{3}^*\right ) \ddot{y}_{3}+b_2(y_3,\dot{y}_2)+\tilde{\tau }_{3} \\[5pt] \tilde{\tau }_1 = \left (I_{11}^*(y_3)-I_{21}^*(y_3)\right ) \ddot{y}_{2}+\left (I_{12}^*(y_3)-I_{22}^*(y_3)\right ) \ddot{y}_{3}+\left (b_1(y_3,\dot{y}_2,\dot{y}_3)-b_2(y_3,\dot{y}_2)\right )+\tilde{\tau }_{2}\\[5pt] \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \tilde{\tau }_3 = I_{3}^* \ddot{y}_1 + \frac{ I_4^*(I_{3}^*-I_4^*) }{k_4} y_1^{(4)} - \frac{c_4 I_4^*(I_{3}^*-I_4^*)}{k_4^2} y_1^{(5)}\\[5pt] \tilde{\tau }_2 = \left (I_{21}^*(y_3)-I_{3}^*\right ) \ddot{y}_{2}+\left (I_{22}^*(y_3)-I_{3}^*\right ) \ddot{y}_{3}+b_2(y_3,\dot{y}_2)+\tilde{\tau }_{3} \\[5pt] \tilde{\tau }_1 = \left (I_{11}^*(y_3)-I_{21}^*(y_3)\right ) \ddot{y}_{2}+\left (I_{12}^*(y_3)-I_{22}^*(y_3)\right ) \ddot{y}_{3}+\left (b_1(y_3,\dot{y}_2,\dot{y}_3)-b_2(y_3,\dot{y}_2)\right )+\tilde{\tau }_{2}\\[5pt] \end{gathered} \end{equation}
The flat variables
![]() $\boldsymbol{y}$
are the same for both cases and are calculated by means of polynomial functions, in particular, an
$\boldsymbol{y}$
are the same for both cases and are calculated by means of polynomial functions, in particular, an
![]() $11$
-th degree polynomial for
$11$
-th degree polynomial for
![]() $y_1$
and a
$y_1$
and a
![]() $5$
-th degree polynomial for
$5$
-th degree polynomial for
![]() $y_2$
and
$y_2$
and
![]() $y_3$
. The polynomial coefficients are calculated by means of Eq. (31), and the initial and final conditions are defined as follows:
$y_3$
. The polynomial coefficients are calculated by means of Eq. (31), and the initial and final conditions are defined as follows:
 \begin{equation} \begin{cases} y_1(t_i) = \sum _{k=1}^4 (q_k)_i \\[5pt] y_1(t_f) = \sum _{k=1}^4 (q_k)_f \\[5pt] y_2(t_i) = q_{1i}\\[5pt] y_2(t_f) = q_{1f}\\[5pt] y_3(t_i) = q_{2i}\\[5pt] y_3(t_f) = q_{2f}\\[5pt] \dot{y}_1(t_i) = \ddot{y}_1(t_i) = y_1^{(3)}(t_i) = y_1^{(4)}(t_i) = y_1^{(5)}(t_i) = \dot{y}_2(t_i) = \ddot{y}_2(t_i) = \dot{y}_3(t_i) = \ddot{y}_3(t_i) = 0\\[5pt] \dot{y}_1(t_f) = \ddot{y}_1(t_f) = y_1^{(3)}(t_f) = y_1^{(4)}(t_f) = y_1^{(5)}(t_f) = \dot{y}_2(t_f) = \ddot{y}_2(t_f) = \dot{y}_3(t_f) = \ddot{y}_3(t_f) = 0 \end{cases} \end{equation}
\begin{equation} \begin{cases} y_1(t_i) = \sum _{k=1}^4 (q_k)_i \\[5pt] y_1(t_f) = \sum _{k=1}^4 (q_k)_f \\[5pt] y_2(t_i) = q_{1i}\\[5pt] y_2(t_f) = q_{1f}\\[5pt] y_3(t_i) = q_{2i}\\[5pt] y_3(t_f) = q_{2f}\\[5pt] \dot{y}_1(t_i) = \ddot{y}_1(t_i) = y_1^{(3)}(t_i) = y_1^{(4)}(t_i) = y_1^{(5)}(t_i) = \dot{y}_2(t_i) = \ddot{y}_2(t_i) = \dot{y}_3(t_i) = \ddot{y}_3(t_i) = 0\\[5pt] \dot{y}_1(t_f) = \ddot{y}_1(t_f) = y_1^{(3)}(t_f) = y_1^{(4)}(t_f) = y_1^{(5)}(t_f) = \dot{y}_2(t_f) = \ddot{y}_2(t_f) = \dot{y}_3(t_f) = \ddot{y}_3(t_f) = 0 \end{cases} \end{equation}
Table III. Parameters of the simulated
![]() $4$
-DOF robot.
$4$
-DOF robot.


Figure 7. Simulated joint variables of the
![]() $4$
-DOF robot considering the torque calculated without and with the viscous friction. An
$4$
-DOF robot considering the torque calculated without and with the viscous friction. An
![]() $11$
-th degree polynomial has been used for
$11$
-th degree polynomial has been used for
![]() $y_1$
and a
$y_1$
and a
![]() $5$
-th degree polynomial for
$5$
-th degree polynomial for
![]() $y_2$
and
$y_2$
and
![]() $y_3$
in both cases.
$y_3$
in both cases.
The simulations are performed considering a motion time equal
![]() $t_f=0.5 \,s$
. The start configuration is
$t_f=0.5 \,s$
. The start configuration is
![]() $\boldsymbol{q}_i=[\!-\!20, -20, -20, 0]\,deg$
, while the end configuration is
$\boldsymbol{q}_i=[\!-\!20, -20, -20, 0]\,deg$
, while the end configuration is
![]() $\boldsymbol{q}_f=[185,35,20,0]\,deg$
. The parameters of
$\boldsymbol{q}_f=[185,35,20,0]\,deg$
. The parameters of
![]() $4$
-DOF robot are summarized in Table III.
$4$
-DOF robot are summarized in Table III.

Figure 8. Simulated trajectories of the end-effector of the
![]() $4$
-DOF robot in
$4$
-DOF robot in
![]() $x-y$
plane considering the torque calculated without and with the viscous friction. An
$x-y$
plane considering the torque calculated without and with the viscous friction. An
![]() $11$
-th degree polynomial has been used for
$11$
-th degree polynomial has been used for
![]() $y_1$
and a
$y_1$
and a
![]() $5$
-th degree polynomial for
$5$
-th degree polynomial for
![]() $y_2$
and
$y_2$
and
![]() $y_3$
in both cases.
$y_3$
in both cases.
Fig. 7 depicts the joint variables of the robot. The behavior of the
![]() $4$
-DOF robot is very similar to the one of the
$4$
-DOF robot is very similar to the one of the
![]() $2$
-DOF robot in which motor torque has been calculated by means of
$2$
-DOF robot in which motor torque has been calculated by means of
![]() $11$
-th degree polynomials (Fig. 6). The introduction of viscous friction has a direct effect on torque
$11$
-th degree polynomials (Fig. 6). The introduction of viscous friction has a direct effect on torque
![]() $\tilde{\tau }_3$
and an indirect effect on the other motor torques through the Newton-Euler recursive formula (Eq. (15)). As a result,
$\tilde{\tau }_3$
and an indirect effect on the other motor torques through the Newton-Euler recursive formula (Eq. (15)). As a result,
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are poorly affected by viscous friction,
$q_2$
are poorly affected by viscous friction,
![]() $q_3$
is slightly affected by viscous friction, and
$q_3$
is slightly affected by viscous friction, and
![]() $q_4$
is strongly affected by viscous friction, especially at the end of the motion, since
$q_4$
is strongly affected by viscous friction, especially at the end of the motion, since
![]() $q_4$
shows oscillations about the final value if viscous friction is not considered in the calculation of torques.
$q_4$
shows oscillations about the final value if viscous friction is not considered in the calculation of torques.
Fig. 8 shows the simulated trajectories of the end-effector considering the torque calculated without and with viscous friction. The difference between the trajectories is relevant near the cusp and at the end of the motion. Moreover, the zoom of the end of the trajectories (depicted in Fig. 8) clearly shows that the end-effector presents oscillations at the end of the planned motion if viscous friction is not taken into account in torque calculation. Such a behavior is not suitable for many applications, in which the motion is considered complete when the amplitude of residual end-effector vibrations is reduced within a small range. Conversely, if torques are calculated taking into account the viscous friction, the system does not show residual vibrations.
These results show that large improvements in point-to-point motion can be achieved with a proper open-loop system without any feedback from the non-actuated joint.
6. Conclusions
If a differentially flat under-actuated robot with friction in the last joint is driven by torques calculated without considering friction in the diffeomorphism, large oscillations occur at the end of the motion. To cope with this problem, a Laplace transform analysis has been proposed, exploiting the linear characteristics of the last rows of the dynamic equations of the system.
First, the proposed method has made it possible to understand the source of the above-mentioned oscillations. Second, a novel approximate method for the calculation of the torques considering viscous friction has been proposed. Third, experimental and numerical results have shown the validity of the proposed method.
The proposed method can be used for improving the control of a planar differentially flat robot, when it is based on the dynamic model of the robot. Let us consider, for example, the control scheme presented in [Reference Agrawal and Sangwan28], which exploits the actuator torques calculated from flat variables and includes a term for friction compensation in the actuated joints. Such a control scheme may be further improved by adding to the calculated torques the friction compensation term proposed in this paper (Eq. 14), so as to take into account the viscous friction of the passive joint in addition to that of the active joints, thus suppressing the oscillations of the last link which occur especially in the execution of fast motions.
The main limit of such method lies in the fact that a small viscous friction of the joint is considered. While this assumption holds true for well-lubricated joints, other forms of friction may be present in actual robotic joints. In this case, the proposed method still can be used considering an equivalent viscous damper that dissipates in a vibration cycle the same amount of energy as the actual dissipative phenomenon. But a further approximation is introduced, which may lead to positioning errors and/or oscillations.
Future developments of this research will be experimental tests on non-actuated joints having different friction characteristics with the extension of the proposed method to consider other forms of friction. Another possible development will be the extension of the proposed method to under-actuated spatial manipulators.
Author contributions
Authors equally contributed to the writing of this paper.
Financial support
This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Competing interests
The authors declare no competing interests exist.
Ethical approval
Not applicable.
Appendix
The terms of the mass matrix of the
![]() $4$
-DOF robot are as follows:
$4$
-DOF robot are as follows:
 \begin{equation} \begin{aligned} I_{11}^*(\boldsymbol{q}) = & \;I_{1}+I_{2}+I_{3}+I_{4}+\\[5pt] &({a_{1}}^2\frac{a_{3}}{a_{c3}}+{a_{2}}^2\frac{a_{3}}{a_{c3}}+{a_{1}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}}+{a_{2}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}}+a_1^2+a_2^2+{a_{3}}^2+a_{3}a_{c3}+\\[5pt] &{a_{1}}^2\frac{a_{g4}}{a_{c4}}+{a_{2}}^2\frac{a_{g4}}{a_{c4}}+{a_{3}}^2\frac{a_{g4}}{a_{c4}}+a_{3}{a_{c3}}\frac{a_{g4}}{a_{c4}}+{a_{g4}}^2+{a_{c4}}a_{g4})m_4+\\[5pt] & \left ({a_{1}}^2+{a_{2}}^2+{a_{1}}^2\frac{a_{g3}}{a_{c3}}+{a_{2}}^2\frac{a_{g3}}{a_{c3}}+{a_{g3}}^2+{a_{c3}}^2\frac{a_{g3}}{a_{c3}}\right )m_3+\\[5pt] & \left ({a_{1}}^2+{a_{g2}}^2\right )m_2+{a_{g1}}^2m_{1}+\frac{2\cos\!\left (q_{2}\right )}{a_{c3}a_{c4}}(a_{1}a_{2}a_{3}a_{c4}m_{4}+a_{1}a_{2}a_{3}a_{g4}m_{4}+a_{1}a_{2}a_{c3}a_{c4}m_{3}+\\[5pt] &a_{1}a_{2}a_{c3}a_{c4}m_{4}+a_{1}a_{2}a_{c4}a_{g3}m_{3}+a_{1}a_{2}a_{c3}a_{g4}m_{4}+a_{1}a_{c3}a_{c4}a_{g2}m_{2}) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} I_{11}^*(\boldsymbol{q}) = & \;I_{1}+I_{2}+I_{3}+I_{4}+\\[5pt] &({a_{1}}^2\frac{a_{3}}{a_{c3}}+{a_{2}}^2\frac{a_{3}}{a_{c3}}+{a_{1}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}}+{a_{2}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}}+a_1^2+a_2^2+{a_{3}}^2+a_{3}a_{c3}+\\[5pt] &{a_{1}}^2\frac{a_{g4}}{a_{c4}}+{a_{2}}^2\frac{a_{g4}}{a_{c4}}+{a_{3}}^2\frac{a_{g4}}{a_{c4}}+a_{3}{a_{c3}}\frac{a_{g4}}{a_{c4}}+{a_{g4}}^2+{a_{c4}}a_{g4})m_4+\\[5pt] & \left ({a_{1}}^2+{a_{2}}^2+{a_{1}}^2\frac{a_{g3}}{a_{c3}}+{a_{2}}^2\frac{a_{g3}}{a_{c3}}+{a_{g3}}^2+{a_{c3}}^2\frac{a_{g3}}{a_{c3}}\right )m_3+\\[5pt] & \left ({a_{1}}^2+{a_{g2}}^2\right )m_2+{a_{g1}}^2m_{1}+\frac{2\cos\!\left (q_{2}\right )}{a_{c3}a_{c4}}(a_{1}a_{2}a_{3}a_{c4}m_{4}+a_{1}a_{2}a_{3}a_{g4}m_{4}+a_{1}a_{2}a_{c3}a_{c4}m_{3}+\\[5pt] &a_{1}a_{2}a_{c3}a_{c4}m_{4}+a_{1}a_{2}a_{c4}a_{g3}m_{3}+a_{1}a_{2}a_{c3}a_{g4}m_{4}+a_{1}a_{c3}a_{c4}a_{g2}m_{2}) \end{aligned} \end{equation}
 \begin{equation} \begin{aligned} I_{12}^*(\boldsymbol{q}) = & \; I_{21}^*(\boldsymbol{q})= I_2+I_3+I_4+\\[5pt] & ({a_{2}}^2+{a_{3}}^2+{a_{g4}}^2+a_{3}{a_{c3}}+{a_{c4}}a_{g4}+{a_{2}}^2\frac{a_{3}}{a_{c3}}+{a_{2}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}}+\\[5pt] &{a_{2}}^2\frac{a_{g4}}{a_{c4}}+a_{3}{a_{c3}}\frac{a_{g4}}{a_{c4}}+{a_{3}}^2\frac{a_{g4}}{a_{c4}})m_4+\\[5pt] & \left ({a_{2}}^2+{a_{g3}}^2+{a_{c3}}a_{g3}+{a_{2}}^2\frac{a_{g3}}{a_{c3}}\right )m_3+\left ({a_{g2}}^2\right )m_2+\\[5pt] & \frac{\cos \left (q_{2}\right )}{a_{c3}a_{c4}} (a_{1}a_{2}a_{3}a_{c4}m_{4}+a_{1}a_{2}a_{3}a_{g4}m_{4}+a_{1}a_{2}a_{c3}a_{c4}m_{3}+a_{1}a_{2}a_{c3}a_{c4}m_{4}+\\[5pt] &a_{1}a_{2}a_{c4}a_{g3}m_{3}+a_{1}a_{2}a_{c3}a_{g4}m_{4}+a_{1}a_{c3}a_{c4}a_{g2}m_{2}) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} I_{12}^*(\boldsymbol{q}) = & \; I_{21}^*(\boldsymbol{q})= I_2+I_3+I_4+\\[5pt] & ({a_{2}}^2+{a_{3}}^2+{a_{g4}}^2+a_{3}{a_{c3}}+{a_{c4}}a_{g4}+{a_{2}}^2\frac{a_{3}}{a_{c3}}+{a_{2}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}}+\\[5pt] &{a_{2}}^2\frac{a_{g4}}{a_{c4}}+a_{3}{a_{c3}}\frac{a_{g4}}{a_{c4}}+{a_{3}}^2\frac{a_{g4}}{a_{c4}})m_4+\\[5pt] & \left ({a_{2}}^2+{a_{g3}}^2+{a_{c3}}a_{g3}+{a_{2}}^2\frac{a_{g3}}{a_{c3}}\right )m_3+\left ({a_{g2}}^2\right )m_2+\\[5pt] & \frac{\cos \left (q_{2}\right )}{a_{c3}a_{c4}} (a_{1}a_{2}a_{3}a_{c4}m_{4}+a_{1}a_{2}a_{3}a_{g4}m_{4}+a_{1}a_{2}a_{c3}a_{c4}m_{3}+a_{1}a_{2}a_{c3}a_{c4}m_{4}+\\[5pt] &a_{1}a_{2}a_{c4}a_{g3}m_{3}+a_{1}a_{2}a_{c3}a_{g4}m_{4}+a_{1}a_{c3}a_{c4}a_{g2}m_{2}) \end{aligned} \end{equation}
 \begin{equation} \begin{aligned} I_{22}^*(\boldsymbol{q}) = & \; I_{2}+I_{3}+I_{4}+({a_{2}}^2+{a_{3}}^2+{a_{g4}}^2+a_{3}a_{c3}+a_{c4}a_{g4}+{a_{2}}^2\frac{a_{3}}{a_{c3}}+{a_{2}}^2\frac{a_{g4}}{a_{c4}}+{a_{3}}^2\frac{a_{g4}}{a_{c4}}+\\[5pt] &a_{3}a_{c3}\frac{a_{g4}}{a_{c4}}+{a_{2}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}})m_4+ \left ({a_{2}}^2+{a_{g3}}^2+a_{c3}a_{g3}+{a_{2}}^2\frac{a_{g3}}{a_{c3}}\right )m_{3}+ \left ({a_{g2}}^2\right )m_{2} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} I_{22}^*(\boldsymbol{q}) = & \; I_{2}+I_{3}+I_{4}+({a_{2}}^2+{a_{3}}^2+{a_{g4}}^2+a_{3}a_{c3}+a_{c4}a_{g4}+{a_{2}}^2\frac{a_{3}}{a_{c3}}+{a_{2}}^2\frac{a_{g4}}{a_{c4}}+{a_{3}}^2\frac{a_{g4}}{a_{c4}}+\\[5pt] &a_{3}a_{c3}\frac{a_{g4}}{a_{c4}}+{a_{2}}^2\frac{a_{3}a_{g4}}{a_{c3}a_{c4}})m_4+ \left ({a_{2}}^2+{a_{g3}}^2+a_{c3}a_{g3}+{a_{2}}^2\frac{a_{g3}}{a_{c3}}\right )m_{3}+ \left ({a_{g2}}^2\right )m_{2} \end{aligned} \end{equation}
 \begin{equation} \begin{aligned} I_{3}^* = & \; I_{3}+I_{4}+\left ({a_{3}}^2+{a_{3}}^2\frac{a_{g4}}{a_{c4}}+{a_{g4}}^2+{a_{c4}}a_{g4}+a_{3}a_{c3}+a_{3}a_{c3}\frac{a_{g4}}{a_{c4}}\right )m_{4} \\[5pt] &+\left ({a_{g3}}^2m_{3}+a_{c3}a_{g3}\right )m_{3} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} I_{3}^* = & \; I_{3}+I_{4}+\left ({a_{3}}^2+{a_{3}}^2\frac{a_{g4}}{a_{c4}}+{a_{g4}}^2+{a_{c4}}a_{g4}+a_{3}a_{c3}+a_{3}a_{c3}\frac{a_{g4}}{a_{c4}}\right )m_{4} \\[5pt] &+\left ({a_{g3}}^2m_{3}+a_{c3}a_{g3}\right )m_{3} \end{aligned} \end{equation}
The Coriolis-centrifugal terms for the
![]() $4$
-DOF robot are as follows:
$4$
-DOF robot are as follows:
 \begin{equation} \begin{aligned} b_{1} (\boldsymbol{q},\dot{\boldsymbol{q}}) = & \; -\frac{1}{a_{c3}a_{c4}}(a_{1}\sin\!\left (q_{2}\right )\left (2\dot{q}_1+\dot{q}_2\right )\dot{q}_2(a_{2}a_{3}a_{c4}m_{4}+a_{2}a_{3}a_{g4}m_{4}+\\[5pt] &a_{2}a_{c3}a_{c4}m_{3}+a_{2}a_{c3}a_{c4}m_{4}+a_{2}a_{c4}a_{g3}m_{3}+a_{2}a_{c3}a_{g4}m_{4}+a_{c3}a_{c4}a_{g2}m_{2})) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} b_{1} (\boldsymbol{q},\dot{\boldsymbol{q}}) = & \; -\frac{1}{a_{c3}a_{c4}}(a_{1}\sin\!\left (q_{2}\right )\left (2\dot{q}_1+\dot{q}_2\right )\dot{q}_2(a_{2}a_{3}a_{c4}m_{4}+a_{2}a_{3}a_{g4}m_{4}+\\[5pt] &a_{2}a_{c3}a_{c4}m_{3}+a_{2}a_{c3}a_{c4}m_{4}+a_{2}a_{c4}a_{g3}m_{3}+a_{2}a_{c3}a_{g4}m_{4}+a_{c3}a_{c4}a_{g2}m_{2})) \end{aligned} \end{equation}
 \begin{equation} \begin{aligned} b_{2} (\boldsymbol{q},\dot{\boldsymbol{q}}) = & \;-\frac{1}{a_{c3}a_{c4}}(a_{1}\sin\!\left (q_{2}\right ){\dot{q}_1}^2(a_{2}a_{3}a_{c4}m_{4}+a_{2}a_{3}a_{g4}m_{4}+a_{2}a_{c3}a_{c4}m_{3}+\\[5pt] &a_{2}a_{c3}a_{c4}m_{4}+a_{2}a_{c4}a_{g3}m_{3}+a_{2}a_{c3}a_{g4}m_{4}+a_{c3}a_{c4}a_{g2}m_{2})) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} b_{2} (\boldsymbol{q},\dot{\boldsymbol{q}}) = & \;-\frac{1}{a_{c3}a_{c4}}(a_{1}\sin\!\left (q_{2}\right ){\dot{q}_1}^2(a_{2}a_{3}a_{c4}m_{4}+a_{2}a_{3}a_{g4}m_{4}+a_{2}a_{c3}a_{c4}m_{3}+\\[5pt] &a_{2}a_{c3}a_{c4}m_{4}+a_{2}a_{c4}a_{g3}m_{3}+a_{2}a_{c3}a_{g4}m_{4}+a_{c3}a_{c4}a_{g2}m_{2})) \end{aligned} \end{equation}