Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T07:14:38.536Z Has data issue: false hasContentIssue false
  • English
  • Français

A Few Points on the Stability of the Solar System

Published online by Cambridge University Press:  07 August 2017

J. Laskar
J. Laskar*
Affiliation:
Bureau des Longitudes, URA CNRS 707 77 Avenue Denfert-Rochereau, 75014, Paris, France e-mail: laskar@friap51.bitnet

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The secular equations which were used to exhibit the chaotic behaviour of the solar system (Laskar, 1989) are established here in a Hamiltonian framework. The integration of the former secular equations over 400 Myr showed that the two resonant arguments 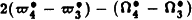and 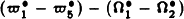given in (Laskar, 1990) present both transitions from libration to circulation. During the circulation of the first argument, temporary libration of the argument 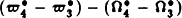is observed, revealing resonance overlap beetween these two resonances, which explains the existence of a large chaotic zone for the motion of the solar system.

Type
Part I - The Planetary System
Information
Symposium - International Astronomical Union , Volume 152: Chaos, Resonance and Collective Dynamical Phenomena in the Solar System , 1992 , pp. 1 - 16
Copyright
Copyright © Kluwer 1992 

References

Arnold, V.I.: 1963, ‘Small denominators and problems of stability of motion in classical and celestial mechanics’, Russ. Math. Surv. , 135, 427 vol 18 N6, 85-192.Google Scholar
Chirikov, B.V.: 1979, ‘A universal instability of many-dimensional oscillator systems’, Phys. Reports 52, 265.Google Scholar
Laskar, J.: 1985, ‘Accurate methods in general planetary theory’, Astron. Astrophys. 144, 133–146.Google Scholar
Laskar, J.: 1986, ‘Secular terms of classical planetary theories using the results of general theory’, Astron. Astrophys. 157, 59–70 Google Scholar
Laskar, J.: 1987, ‘Secular evolution, proper modes and resonances in the inner Solar System’, in Resonances in the Solar System , Sidlichovsky, M. ed., Prague.Google Scholar
Laskar, J.: 1988, ‘Secular evolution of the Solar System over 10 million years’, Astron. Astrophys. 198, 341–362.Google Scholar
Laskar, J.: 1989, ‘A numerical experiment on the chaotic behaviour of the Solar System’, Nature , 338, 237–238.Google Scholar
Laskar, J.: 1990, ‘The chaotic motion of the solar system. A numerical estimate of the size of the chaotic zones’, Icarus , 88,266–291.CrossRefGoogle Scholar
Laskar, J.: 1991, ‘Analytical framework in Poincaré variables for the motion of the solar system’, in Predictability, Stability and Chaos in n-body Dynamical Systems , Roy, A., ed., Plenum Press.Google Scholar
Laskar, J., Quinn, T., Tremaine, S.: 1991, ‘Confirmation of Resonant Structure in the Solar System’, submitted to Icarus. Google Scholar
Laskar, J., Froeschlé, Cl., Celletti, A.: 1991 ‘The Measure of Chaos by the Numerical Analysis of the Fundamental Frequencies. Application to the Standard Mapping’, submitted to Physica D. Google Scholar
Poincaré, H.: 1892, Méthodes Nouvelles de la Mécanique Celeste Vol. 1 (Gauthier-Villars, Paris).Google Scholar
Poincaré, H.: 1896, ‘Une forme nouvelle des équations du problème des trois corps’, C. R. Acad. Sc. 123, 1031–1035.Google Scholar
Quinn, T.R., Tremaine, S., Duncan, M.: 1991, ‘A three million year integration of the Earth's orbit’, Astron. J. 101, 2287–2305.Google Scholar
Sussman, G.J., Wisdom, J.: 1988, ‘Numerical evidence that the motion of Pluto is chaotic’. Science 241, 433–437.Google Scholar
Sussman, G.J., Wisdom, J.: 1991, these proceedings Google Scholar
Williams, J.G.: 1984, ‘Determining Asteroid Masses from Perturbations on Mars’, Icarus , 57, 1–13.Google Scholar
Wisdom, J.: 1983, ‘Chaotic Behaviour and the origin of the 3/1 Kirkwood Gap’, Icarus , 56, 51–74 Google Scholar