No CrossRef data available.
Published online by Cambridge University Press: 03 August 2017
It is shown that the solutions for the non-linear equations governing the motion of a stratified self-gravitating isothermal fluid are generated by a sine-Gordon equation (SG) which has well-known soliton solutions. Starting with two solutions of the SG-equation which are related via an auto-Baecklund-transformation, the physical quantities, density, velocity and gravitational potential are expressed in a parametric form in terms of characteristic coordinates. The zero-solution and the one-soliton solution of SG generate a single hump in the density moving with constant velocity. The typical non-linear feature is the relation between amplitude A and width 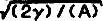 (y = square of the speed of sound). The 1-soliton together with the 2-sollton solution of SG produces two moving humps in the density which come to rest asymptotically. As a result of the interaction the ratio amplitude/width is different from the corresponding ratio of the single soliton. Due to a certain exchange symmetry in the transformation procedure relating the SG to the gravity system it is possible to generate another solution out of the 2-soliton. Which represents a single hump moving on a homogeneous background. The remarkable property is that the density becomes infinite in a finite time depending on the amplitude. The “breather”-solutlon of SG produces a density distribution that represents two pulses colliding onto a central hump at rest which are separated from each other by a discontinuity in the density and the velocity field. These solutions may have applications to the non-linear evolution of flat structures arising in the process of galaxy formation.
(y = square of the speed of sound). The 1-soliton together with the 2-sollton solution of SG produces two moving humps in the density which come to rest asymptotically. As a result of the interaction the ratio amplitude/width is different from the corresponding ratio of the single soliton. Due to a certain exchange symmetry in the transformation procedure relating the SG to the gravity system it is possible to generate another solution out of the 2-soliton. Which represents a single hump moving on a homogeneous background. The remarkable property is that the density becomes infinite in a finite time depending on the amplitude. The “breather”-solutlon of SG produces a density distribution that represents two pulses colliding onto a central hump at rest which are separated from each other by a discontinuity in the density and the velocity field. These solutions may have applications to the non-linear evolution of flat structures arising in the process of galaxy formation.