Article contents
Topology of the Negative Energy-Manifold of the Kepler Motion
Published online by Cambridge University Press: 14 August 2015
Extract
The motion of a particle of mass m according to the central force of Newton, is denoted by
 where K is a constant. x=0 corresponds to singular points of this equations. The domain of (1), denoted by
where K is a constant. x=0 corresponds to singular points of this equations. The domain of (1), denoted by 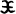 = (R3 −{0})×R3, is called the phase space of the Kepler motion. In the sequel we set m=K=1 for simplicity and also transform the independent variable from t to s by dt =|x|ds (x≠0), then the Kepler motion in the phase space
= (R3 −{0})×R3, is called the phase space of the Kepler motion. In the sequel we set m=K=1 for simplicity and also transform the independent variable from t to s by dt =|x|ds (x≠0), then the Kepler motion in the phase space 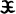 is written as
is written as
 Further, we shall confine the following discussion to the case of the negative energy value, except the preliminary discussion.
Further, we shall confine the following discussion to the case of the negative energy value, except the preliminary discussion.
- Type
- Part I: Stability, N- and 3-Body Problems, Variable Mass
- Information
- Symposium - International Astronomical Union , Volume 81: Dynamics of the Solar System , 1979 , pp. 45 - 48
- Copyright
- Copyright © Reidel 1979
References
- 1
- Cited by


