Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T17:18:26.920Z Has data issue: false hasContentIssue false
  • English
  • Français

MV-Datalog+-: Effective Rule-based Reasoning with Uncertain Observations

Published online by Cambridge University Press:  26 July 2022

MATTHIAS LANZINGER ,
STEFANO SFERRAZZA Open the ORCID record for STEFANO SFERRAZZA [Opens in a new window]  and
GEORG GOTTLOB
MATTHIAS LANZINGER
Affiliation:
University of Oxford, Oxford OX1 2JD, UK (e-mail: matthias.lanzinger@cs.ox.ac.uk)
STEFANO SFERRAZZA
Affiliation:
University of Oxford, Oxford OX1 2JD, UK, Technische Universität Wien, Vienna, Austria (e-mail: stefano.sferrazza@cs.ox.ac.uk)
GEORG GOTTLOB
Affiliation:
University of Oxford, Oxford OX1 2JD, UK (e-mail: georg.gottlob@cs.ox.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Modern applications combine information from a great variety of sources. Oftentimes, some of these sources, like machine-learning systems, are not strictly binary but associated with some degree of (lack of) confidence in the observation. We propose MV-Datalog and 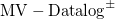$\mathrm{MV-Datalog}^\pm$ as extensions of Datalog and 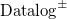$\mathrm{Datalog}^\pm$ , respectively, to the fuzzy semantics of infinite-valued Łukasiewicz logic 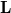$\mathbf{L}$ as languages for effectively reasoning in scenarios where such uncertain observations occur. We show that the semantics of MV-Datalog exhibits similar model theoretic properties as Datalog. In particular, we show that (fuzzy) entailment can be decided via minimal fuzzy models. We show that when they exist, such minimal fuzzy models are unique and can be characterised in terms of a linear optimisation problem over the output of a fixed-point procedure. On the basis of this characterisation, we propose similar many-valued semantics for rules with existential quantification in the head, extending 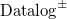$\mathrm{Datalog}^\pm$ .

Keywords

Datalogfuzzy logic programminglogic programmingŁukasiewiczlogicuncertainty in AIDatalog±
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 22 , Issue 5: 38th International Conference on Logic Programming Special Issue II , September 2022 , pp. 678 - 692
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Stefano Sferrazza was supported by the Austrian Science Fund (FWF):P30930. Georg Gottlob is a Royal Society Research Professor and acknowledges support by the Royal Society in this role through the “RAISON DATA” project (Reference No. RP\R1\201074). Matthias Lanzinger acknowledges support by the Royal Society “RAISON DATA” project (Reference No. RP\R1\201074).

References

Achs, Á. and Kiss, A. 1995. Fuzzy extension of datalog. Acta Cybernetica 12, 2, 153–166.Google Scholar
Bach, S. H., Broecheler, M., Huang, B. and Getoor, L. 2017. Hinge-Loss Markov random fields and probabilistic soft logic. Journal of Machine Learning Research 18, 109:1–109:67.Google Scholar
Bellomarini, L., Gottlob, G., Pieris, A. and Sallinger, E. 2017. Swift logic for big data and knowledge graphs. In Proceedings of IJCAI. ijcai.org, 2–10.Google Scholar
Bellomarini, L., Laurenza, E., Sallinger, E. and Sherkhonov, E. 2020. Reasoning under uncertainty in knowledge graphs. In RuleML+RR. Springer, 131–139.Google Scholar
Bobillo, F. and Straccia, U. 2016. The fuzzy ontology reasoner fuzzydl. Knowledge-Based Systems 95, 12–34.CrossRefGoogle Scholar
Borgwardt, S., Cerami, M. and PeÑaloza, R. 2017. Łukasiewicz fuzzy EL is undecidable. In Proceedings of DL. CEUR Workshop Proceedings, vol. 1879. CEUR-WS.org.Google Scholar
Borgwardt, S. and PeÑaloza, R. 2017. Fuzzy description logics - A survey. In Proceedings of SUM. Lecture Notes in Computer Science, vol. 10564. Springer, 31–45.Google Scholar
CalÌ, A., Gottlob, G. and Kifer, M. 2013. Taming the infinite chase: Query answering under expressive relational constraints. JAIR 48, 115–174.CrossRefGoogle Scholar
CalÌ, A., Gottlob, G. and Lukasiewicz, T. 2012. A general Datalog-based framework for tractable query answering over ontologies. Journal of Web Semantics 14, 57–83.CrossRefGoogle Scholar
Cavallo, R. and Pittarelli, M. 1987. The theory of probabilistic databases. In VLDB’87. Morgan Kaufmann, 71–81.Google Scholar
Dantsin, E., Eiter, T., Gottlob, G. and Voronkov, A. 2001. Complexity and expressive power of logic programming. ACM Computing Surveys 33, 3, 374–425.CrossRefGoogle Scholar
Ebrahim, R. 2001. Fuzzy logic programming. Fuzzy Sets and Systems 117, 2, 215–230.CrossRefGoogle Scholar
Fagin, R., Kolaitis, P. G., Miller, R. J. and Popa, L. 2005. Data exchange: Semantics and query answering. Theoretical Computer Science 336, 1, 89–124.CrossRefGoogle Scholar
Fjellstad, A. and Olsen, J.-F. 2021. ${\mathrm{IKT}^{\omega }}$ and Łukasiewicz-Models. Notre Dame Journal of Formal Logic 62, 2, 247–256.Google Scholar
HÁjek, P. 1998. Metamathematics of Fuzzy Logic. Trends in Logic, vol. 4. Kluwer.Google Scholar
Iranzo, P. J. and SÁenz-PÉrez, F. 2018. A fuzzy datalog deductive database system. IEEE Transactions on Fuzzy Systems 26, 5, 2634–2648.CrossRefGoogle Scholar
Khachiyan, L. G. 1979. A polynomial algorithm in linear programming. In Doklady Akademii Nauk, vol. 244. Russian Academy of Sciences, 1093–1096.Google Scholar
Lanzinger, M., Sferrazza, S. and Gottlob, G. 2022. Mv-datalog+-: Effective rule-based reasoning with uncertain observations. CoRR, abs/2202.01718.CrossRefGoogle Scholar
Lee, H. S., Jung, H., Agarwal, A. A. and Kim, J. 2017. Can deep neural networks match the related objects?: A survey on imagenet-trained classification models. CoRR, abs/1709.03806.Google Scholar
Lukasiewicz, T. and Straccia, U. 2008. Managing uncertainty and vagueness in description logics for the semantic web. Journal of Web Semantics 6, 4, 291–308.CrossRefGoogle Scholar
Maier, D., Tekle, K. T., Kifer, M. and Warren, D. S. 2018. Datalog: Concepts, history, and outlook. In Declarative Logic Programming: Theory, Systems, and Applications. ACM/Morgan & Claypool.CrossRefGoogle Scholar
Mishkin, D., Sergievskiy, N. and Matas, J. 2017. Systematic evaluation of convolution neural network advances on the imagenet. Computer Vision and Image Understanding 161, 11–19.CrossRefGoogle Scholar
Preining, N. 2010. GÖdel logics - A survey. In Proceedings of LPAR. Lecture Notes in Computer Science, vol. 6397. Springer, 30–51.Google Scholar
Raedt, L. D., Kimmig, A. and Toivonen, H. 2007. Problog: A probabilistic prolog and its application in link discovery. In Proceedings of IJCAI, 2462–2467.Google Scholar
Richardson, M. and Domingos, P. M. 2006. Markov logic networks. Machine Learning 62, 1–2, 107–136.CrossRefGoogle Scholar
Stoilos, G., Stamou, G. B., Pan, J. Z., Tzouvaras, V. and Horrocks, I. 2007. Reasoning with very expressive fuzzy description logics. Journal of Artificial Intelligence Research 30, 273–320.CrossRefGoogle Scholar
Suciu, D., Olteanu, D., RÉ, C. and Koch, C. 2011. Probabilistic Databases. Synthesis Lectures on Data Management. Morgan & Claypool Publishers.Google Scholar
VojtÁs, P. 2001. Fuzzy logic programming. Fuzzy Sets and Systems 124, 3, 361–370.CrossRefGoogle Scholar
Supplementary material: PDF

Lanzinger et al. supplementary material

Lanzinger et al. supplementary material

Download Lanzinger et al. supplementary material(PDF)
PDF 309.3 KB