Article contents
Deriving conclusions from non-monotonic cause-effect relations*
Published online by Cambridge University Press: 14 October 2016
Abstract
We present an extension of Logic Programming (under stable models semantics) that, not only allows concluding whether a true atom is a cause of another atom, but also deriving new conclusions from these causal-effect relations. This is expressive enough to capture informal rules like “if some agent's actions 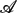 have been necessary to cause an event E then conclude atom caused(
have been necessary to cause an event E then conclude atom caused(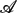 , E),” something that, to the best of our knowledge, had not been formalised in the literature. To this aim, we start from a first attempt that proposed extending the syntax of logic programs with so-called causal literals. These causal literals are expressions that can be used in rule bodies and allow inspecting the derivation of some atom A in the program with respect to some query function ψ. Depending on how these query functions are defined, we can model different types of causal relations such as sufficient, necessary or contributory causes, for instance. The initial approach was specifically focused on monotonic query functions. This was enough to cover sufficient cause-effect relations but, unfortunately, necessary and contributory are essentially non-monotonic. In this work, we define a semantics for non-monotonic causal literals showing that, not only extends the stable model semantics for normal logic programs, but also preserves many of its usual desirable properties for the extended syntax. Using this new semantics, we provide precise definitions of necessary and contributory causal relations and briefly explain their behaviour on a pair of typical examples from the Knowledge Representation literature.
, E),” something that, to the best of our knowledge, had not been formalised in the literature. To this aim, we start from a first attempt that proposed extending the syntax of logic programs with so-called causal literals. These causal literals are expressions that can be used in rule bodies and allow inspecting the derivation of some atom A in the program with respect to some query function ψ. Depending on how these query functions are defined, we can model different types of causal relations such as sufficient, necessary or contributory causes, for instance. The initial approach was specifically focused on monotonic query functions. This was enough to cover sufficient cause-effect relations but, unfortunately, necessary and contributory are essentially non-monotonic. In this work, we define a semantics for non-monotonic causal literals showing that, not only extends the stable model semantics for normal logic programs, but also preserves many of its usual desirable properties for the extended syntax. Using this new semantics, we provide precise definitions of necessary and contributory causal relations and briefly explain their behaviour on a pair of typical examples from the Knowledge Representation literature.
Information
- Type
- Regular Papers
- Information
- Theory and Practice of Logic Programming , Volume 16 , Special Issue 5-6: 32nd International Conference on Logic Programming , September 2016 , pp. 670 - 687
- Copyright
- Copyright © Cambridge University Press 2016
Footnotes
This research was partially supported by Spanish Project TIN2013-42149-P.
References
- 6
- Cited by

