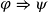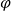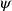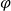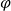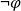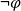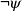1 Introduction
People use conditional sentences and reason with them in everyday life. From an early stage of artificial intelligence (AI), researchers represent conditional sentences as if-then rules and perform deductive inference using them. Production systems or logic programming are examples of this type of systems. However, human conditional reasoning is not always logically valid. In psychology and cognitive science, it is well known that humans are more likely to perform logically invalid but pragmatic inference. For instance, consider the following three sentences:
S: If the team wins the first round tournament, then it advances to the final round.
P: The team wins the first round tournament.
C: The team advances to the final round.
Given the conditional sentence S and the premise P, affirming the antecedent (AA) (or modus ponens) concludes the consequence C. Given S and the negation of the consequence
![]() $\neg\, C$
, denying the consequent (DC) (or modus tollens) concludes the negation of the premise
$\neg\, C$
, denying the consequent (DC) (or modus tollens) concludes the negation of the premise
![]() $\neg\, P$
. AA and DC are logically valid. On the other hand, people often infer P from S and C or infer
$\neg\, P$
. AA and DC are logically valid. On the other hand, people often infer P from S and C or infer
![]() $\neg\, C$
from S and
$\neg\, C$
from S and
![]() $\neg\, P$
. The former is called affirming the consequent (AC), and the latter is called denying the antecedent (DA). Both AC and DA are logically invalid and often called logical fallacies.
$\neg\, P$
. The former is called affirming the consequent (AC), and the latter is called denying the antecedent (DA). Both AC and DA are logically invalid and often called logical fallacies.
In the pragmatics of conditional reasoning, it is assumed that a conditional sentence is often interpreted as bi-conditional, that is, “ if” is interpreted as “ if and only if,” and such conditional perfection produces AC or DA as invited inference (Geis and Zwicky Reference Geis and Zwicky1971; Horn Reference Horn2000). Psychological studies empirically show that a conditional sentence “p if q" is rephrased into the form “p only if q" with greater frequency for permission/obligation statements (Cheng and Holyoak Reference Cheng and Holyoak1985; Byrne Reference Byrne2005). For instance, the sentence “a customer can drink an alcoholic beverage if he is over 18" is rephrased into “a customer can drink an alcoholic beverage only if he is over 18." It is also reported that AA is easier than DC when a conditional is given as “ if p then q." When a conditional is given as “p only if q," on the other hand, it is rephrased as “ if not q then not p" and this paraphrase yields a directionality opposite which makes DC easier than AA (Braine Reference Braine1978). The fact that people do not necessarily make inferences as in standard logic brings several proposals of new interpretation of conditional sentences in cognitive psychology. Mental logic (Braine and O’Brien 1998) interprets “ if’’ as conveying supposition and introduces a set of pragmatic inference schemas for if-conditionals. Mental model theory (Johnson-Laird Reference Johnson-Laird1983), on the other hand, considers that the meanings of conditionals are not truth-functional, and represents the meaning of a conditional sentence by models of the possibilities compatible with the sentence. A probabilistic approach interprets a conditional sentence “
![]() $p\Rightarrow q$
" in terms of conditional probability
$p\Rightarrow q$
" in terms of conditional probability
![]() $P(q\mid p)$
, then the acceptance rates of four conditional inferences are represented by their respective conditional probabilities (Oaksford and Chater Reference Oaksford and Chater2001). Eichhorn et al. (Reference Eichhorn, Kern-Isberner and Ragni2018) use conditional logic and define inference patterns as combination of four inference rules (AA, DC, AC, DA). Given a conditional sentence “ if p then q," four possible worlds (combination of truth values of p and q) are considered. An inference in each pattern is then defined by imposing corresponding constraints on the plausibility relation over the worlds.
$P(q\mid p)$
, then the acceptance rates of four conditional inferences are represented by their respective conditional probabilities (Oaksford and Chater Reference Oaksford and Chater2001). Eichhorn et al. (Reference Eichhorn, Kern-Isberner and Ragni2018) use conditional logic and define inference patterns as combination of four inference rules (AA, DC, AC, DA). Given a conditional sentence “ if p then q," four possible worlds (combination of truth values of p and q) are considered. An inference in each pattern is then defined by imposing corresponding constraints on the plausibility relation over the worlds.
In this way, the need of considering the pragmatics of conditional reasoning has been widely recognized in psychology and cognitive science. On the other hand, relatively little attention has been paid for realizing such pragmatic inference in computational logic or logic programming (Stenning and Lambalgen 2008; Kowalski Reference Kowalski2011). From a practical perspective, however, people would expect AI to reason like humans, that is, one would expect AI to conclude P from S and C, or
![]() $\neg\, C$
from S and
$\neg\, C$
from S and
![]() $\neg\, P$
in the introductory example, rather than conclude unknown. Logic programming is a context-independent language and has a general-purpose inference mechanism by its nature. By contrast, pragmatic inference is governed by context-sensitive mechanisms, rather than context-free and general-purpose mechanisms (Cheng and Holyoak Reference Cheng and Holyoak1985; Cosmides and Tooby Reference Cosmides, Tooby, Barkow, Cosmides and Tooby1992). As argued by Dietz et al. (Reference Dietz, Hölldobler and Ragni2012), computational approaches to explain human reasoning should be cognitively adequate, that is, they appropriately represent human knowledge ( conceptually adequate) and computations behave similarly to human reasoning ( inferentially adequate). Then if we use logic programming for representing knowledge in daily life, it is useful to have a mechanism of automatic transformation of a knowledge base to simulate human reasoning depending on the context in which conditional sentences are used. That is, transform a program to a conceptually adequate form in order to make computation in the program inferentially adequate.
$\neg\, P$
in the introductory example, rather than conclude unknown. Logic programming is a context-independent language and has a general-purpose inference mechanism by its nature. By contrast, pragmatic inference is governed by context-sensitive mechanisms, rather than context-free and general-purpose mechanisms (Cheng and Holyoak Reference Cheng and Holyoak1985; Cosmides and Tooby Reference Cosmides, Tooby, Barkow, Cosmides and Tooby1992). As argued by Dietz et al. (Reference Dietz, Hölldobler and Ragni2012), computational approaches to explain human reasoning should be cognitively adequate, that is, they appropriately represent human knowledge ( conceptually adequate) and computations behave similarly to human reasoning ( inferentially adequate). Then if we use logic programming for representing knowledge in daily life, it is useful to have a mechanism of automatic transformation of a knowledge base to simulate human reasoning depending on the context in which conditional sentences are used. That is, transform a program to a conceptually adequate form in order to make computation in the program inferentially adequate.
In this paper, we realize human conditional reasoning in answer set programming (ASP) (Gelfond and Lifschitz Reference Gelfond and Lifschitz1991). ASP is one of the most popular frameworks that realize declarative knowledge representation and commonsense reasoning. ASP is a language of logic programming and conditional sentences are represented by rules in a program. Inference in ASP is deduction based on default logic (Reiter Reference Reiter1980), while modus tollens or DC is not considered in ASP. AC and DA are partly realized by abductive logic programming (Kakas et al. Reference Kakas, Kowalski and Toni1992) and program completion (Clark Reference Clark and Press1978), respectively. As will be argued in this paper, however, AC and DA produce different results from them in general. We realize pragmatic AC and DA inferences as well as DC inference in ASP in a uniform and modular way. We introduce the notions of AC completion, DC completion, DA completion, and their variants. We investigate formal properties of those completions and characterize human reasoning tasks in cognitive psychology. We also address applications to commonsense reasoning in AI. The rest of this paper is organized as follows. Section 2 reviews basic notions of ASP programs considered in this paper. Section 3 introduces different types of completions for human conditional reasoning, and Section 4 presents their variants as default reasoning. Section 5 characterizes human reasoning tasks in the literature, and Section 6 addresses applications to commonsense reasoning. Section 7 discusses related works and Section 8 summarizes the paper.
2 Preliminaries
In this paper, we consider logic programs with disjunction, default negation, and explicit negation. A general extended disjunctive program (GEDP) (Lifschitz andWoo Reference Lifschitz, Woo and Kaufmann1992; Inoue and Sakama Reference Inoue and Sakama1998)
![]() $\Pi$
is a set of rules of the form:
$\Pi$
is a set of rules of the form:
where
![]() $L_i$
’s
$L_i$
’s
![]() $(1\le i\le n)$
are (positive or negative) literals and
$(1\le i\le n)$
are (positive or negative) literals and
![]() $0\leq k\leq l\leq m\leq n$
. A program might contain two types of negation: default negation (or negation as failure) not and explicit negation
$0\leq k\leq l\leq m\leq n$
. A program might contain two types of negation: default negation (or negation as failure) not and explicit negation
![]() $\neg$
. For any literal L,
$\neg$
. For any literal L,
![]() $not\,L$
is called an NAF-literal and define
$not\,L$
is called an NAF-literal and define
![]() $\neg\neg L=L$
. We often use the letter
$\neg\neg L=L$
. We often use the letter
![]() $\ell$
to mean either a literal L or an NAF-literal
$\ell$
to mean either a literal L or an NAF-literal
![]() $not\,L$
. The left of “
$not\,L$
. The left of “
![]() $\leftarrow$
" is a disjunction of literals and NAF-literals (called head), and the right of “
$\leftarrow$
" is a disjunction of literals and NAF-literals (called head), and the right of “
![]() $\leftarrow$
" is a conjunction of literals and NAF-literals (called body). Given a rule r of the form (1), define
$\leftarrow$
" is a conjunction of literals and NAF-literals (called body). Given a rule r of the form (1), define
![]() $head^+(r)=\{L_1,\ldots,L_k\}$
,
$head^+(r)=\{L_1,\ldots,L_k\}$
,
![]() $head^-(r)=\{L_{k+1},\ldots,L_l\}$
,
$head^-(r)=\{L_{k+1},\ldots,L_l\}$
,
![]() $body^+(r)=\{L_{l+1},\ldots,L_m\}$
, and
$body^+(r)=\{L_{l+1},\ldots,L_m\}$
, and
![]() $body^-(r)=\{L_{m+1},\ldots,L_n\}$
. A rule (1) is called a fact if
$body^-(r)=\{L_{m+1},\ldots,L_n\}$
. A rule (1) is called a fact if
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
, and it is called a constraint if
$body^{+}(r)=body^{-}(r)={\varnothing}$
, and it is called a constraint if
![]() $head^+(r)=head^-(r)={\varnothing}$
. A GEDP
$head^+(r)=head^-(r)={\varnothing}$
. A GEDP
![]() $\Pi$
is called not- free if
$\Pi$
is called not- free if
![]() $head^-(r)=body^-(r)={\varnothing}$
for each rule r in
$head^-(r)=body^-(r)={\varnothing}$
for each rule r in
![]() $\Pi$
.
$\Pi$
.
A GEDP
![]() $\Pi$
coincides with an extended disjunctive program (EDP) of Gelfond and Lifschitz (Reference Gelfond and Lifschitz1991) if
$\Pi$
coincides with an extended disjunctive program (EDP) of Gelfond and Lifschitz (Reference Gelfond and Lifschitz1991) if
![]() $head^-(r)={\varnothing}$
for any rule r in
$head^-(r)={\varnothing}$
for any rule r in
![]() $\Pi$
. An EDP
$\Pi$
. An EDP
![]() $\Pi$
is called (i) an extended logic program (ELP) if
$\Pi$
is called (i) an extended logic program (ELP) if
![]() $\mid\!\! head^+(r)\!\!\mid\,\le 1$
for any
$\mid\!\! head^+(r)\!\!\mid\,\le 1$
for any
![]() $r\in\Pi$
and (ii) a normal disjunctive program (NDP) if
$r\in\Pi$
and (ii) a normal disjunctive program (NDP) if
![]() $\Pi$
contains no negative literal. An NDP
$\Pi$
contains no negative literal. An NDP
![]() $\Pi$
is called (i) a positive disjunctive program (PDP) if
$\Pi$
is called (i) a positive disjunctive program (PDP) if
![]() $\Pi$
contains no NAF-literal and (ii) a normal logic program (NLP) if
$\Pi$
contains no NAF-literal and (ii) a normal logic program (NLP) if
![]() $\mid\!\! head^+(r)\!\!\mid\,\le 1$
for any
$\mid\!\! head^+(r)\!\!\mid\,\le 1$
for any
![]() $r\in\Pi$
. In this paper, we consider ground programs containing no variable and a program means a (ground) GEDP unless stated otherwise.
$r\in\Pi$
. In this paper, we consider ground programs containing no variable and a program means a (ground) GEDP unless stated otherwise.
Let Lit be the set of all ground literals in the language of a program. A set of ground literals
![]() $S\subseteq Lit$
satisfies a ground rule r of the form (1) iff
$S\subseteq Lit$
satisfies a ground rule r of the form (1) iff
![]() $body^+(r)\subseteq S$
and
$body^+(r)\subseteq S$
and
![]() $body^-(r)\cap S={\varnothing}$
imply either
$body^-(r)\cap S={\varnothing}$
imply either
![]() $head^+(r)\cap S\neq{\varnothing}$
or
$head^+(r)\cap S\neq{\varnothing}$
or
![]() $head^-(r)\not\subseteq S$
. In particular, when
$head^-(r)\not\subseteq S$
. In particular, when
![]() $head^+(r)=head^-(r)={\varnothing}$
,
$head^+(r)=head^-(r)={\varnothing}$
,
![]() $S\subseteq Lit$
satisfies a constraint r iff
$S\subseteq Lit$
satisfies a constraint r iff
![]() $body^+(r)\not\subseteq S$
or
$body^+(r)\not\subseteq S$
or
![]() $body^-(r)\cap S\neq{\varnothing}$
. The answer sets of a GEDP are defined by the following two steps. First, let
$body^-(r)\cap S\neq{\varnothing}$
. The answer sets of a GEDP are defined by the following two steps. First, let
![]() $\Pi$
be a not-free GEDP and
$\Pi$
be a not-free GEDP and
![]() $S\subseteq Lit$
. Then, S is an answer set of
$S\subseteq Lit$
. Then, S is an answer set of
![]() $\Pi$
iff S is a minimal set satisfying the conditions: (i) S satisfies every rule from
$\Pi$
iff S is a minimal set satisfying the conditions: (i) S satisfies every rule from
![]() $\Pi$
, that is, for each ground rule:
$\Pi$
, that is, for each ground rule:
from
![]() $\Pi$
,
$\Pi$
,
![]() $\{L_{l+1},\ldots,L_m\}\subseteq S$
implies
$\{L_{l+1},\ldots,L_m\}\subseteq S$
implies
![]() $\{L_1,\ldots,L_k\}\cap S\ne{\varnothing}$
. (ii) If S contains a pair of complementary literals L and
$\{L_1,\ldots,L_k\}\cap S\ne{\varnothing}$
. (ii) If S contains a pair of complementary literals L and
![]() $\neg L$
, then
$\neg L$
, then
![]() $S=Lit$
.Footnote 1
$S=Lit$
.Footnote 1
Second, let
![]() $\Pi$
be any GEDP and
$\Pi$
be any GEDP and
![]() $S\subseteq Lit$
. The reduct
$S\subseteq Lit$
. The reduct
![]() $\Pi^S$
of
$\Pi^S$
of
![]() $\Pi$
by S is a not-free EDP obtained as follows: a rule
$\Pi$
by S is a not-free EDP obtained as follows: a rule
![]() $r^S$
of the form (2) is in
$r^S$
of the form (2) is in
![]() $\Pi^S$
iff there is a ground rule r of the form (1) from
$\Pi^S$
iff there is a ground rule r of the form (1) from
![]() $\Pi$
such that
$\Pi$
such that
![]() $head^-(r)\subseteq S$
and
$head^-(r)\subseteq S$
and
![]() $body^-(r)\cap S={\varnothing}$
. For programs of the form
$body^-(r)\cap S={\varnothing}$
. For programs of the form
![]() $\Pi^S$
, their answer sets have already been defined. Then, S is an answer set of
$\Pi^S$
, their answer sets have already been defined. Then, S is an answer set of
![]() $\Pi$
iff S is an answer set of
$\Pi$
iff S is an answer set of
![]() $\Pi^S$
.
$\Pi^S$
.
When a program
![]() $\Pi$
is an EDP, the above definition of answer sets coincides with that given by Gelfond and Lifschitz (Reference Gelfond and Lifschitz1991). It is shown that every answer set of a GEDP
$\Pi$
is an EDP, the above definition of answer sets coincides with that given by Gelfond and Lifschitz (Reference Gelfond and Lifschitz1991). It is shown that every answer set of a GEDP
![]() $\Pi$
satisfies every rule from
$\Pi$
satisfies every rule from
![]() $\Pi$
(Inoue and Sakama Reference Inoue and Sakama1998). An answer set is consistent if it is not Lit. A program
$\Pi$
(Inoue and Sakama Reference Inoue and Sakama1998). An answer set is consistent if it is not Lit. A program
![]() $\Pi$
is consistent if it has a consistent answer set; otherwise,
$\Pi$
is consistent if it has a consistent answer set; otherwise,
![]() $\Pi$
is inconsistent. When a program
$\Pi$
is inconsistent. When a program
![]() $\Pi$
is inconsistent, there are two different cases. If
$\Pi$
is inconsistent, there are two different cases. If
![]() $\Pi$
has the single answer set Lit,
$\Pi$
has the single answer set Lit,
![]() $\Pi$
is called contradictory; else if
$\Pi$
is called contradictory; else if
![]() $\Pi$
has no answer set,
$\Pi$
has no answer set,
![]() $\Pi$
is called incoherent. The difference of two cases is illustrated by the following example.
$\Pi$
is called incoherent. The difference of two cases is illustrated by the following example.
Example 2.1 The program
![]() $\Pi_1\,{=}\,\{\,p\leftarrow not\,q,\;\; \neg p\leftarrow \,\}$
is incoherent, while
$\Pi_1\,{=}\,\{\,p\leftarrow not\,q,\;\; \neg p\leftarrow \,\}$
is incoherent, while
![]() $\Pi_2\,{=}\,\{\,p\leftarrow q,\;\;~q\leftarrow,\;\; \neg p\leftarrow\,\}$
is contradictory. Note that Lit is not the answer set of
$\Pi_2\,{=}\,\{\,p\leftarrow q,\;\;~q\leftarrow,\;\; \neg p\leftarrow\,\}$
is contradictory. Note that Lit is not the answer set of
![]() $\Pi_1$
because Lit is not the answer set of
$\Pi_1$
because Lit is not the answer set of
![]() $\Pi_1^{Lit}=\{\,\neg p\leftarrow\,\}$
.
$\Pi_1^{Lit}=\{\,\neg p\leftarrow\,\}$
.
We write
![]() $\Pi\models_c L$
(resp.
$\Pi\models_c L$
(resp.
![]() $\Pi\models_s L$
) if a literal L is included in some (resp. every) consistent answer set of
$\Pi\models_s L$
) if a literal L is included in some (resp. every) consistent answer set of
![]() $\Pi$
.Footnote 2 Two programs
$\Pi$
.Footnote 2 Two programs
![]() $\Pi_1$
and
$\Pi_1$
and
![]() $\Pi_2$
are equivalent if they have the same set of answer sets. Two programs
$\Pi_2$
are equivalent if they have the same set of answer sets. Two programs
![]() $\Pi_1$
and
$\Pi_1$
and
![]() $\Pi_2$
are strongly equivalent if
$\Pi_2$
are strongly equivalent if
![]() $\Pi_1\cup\Pi$
and
$\Pi_1\cup\Pi$
and
![]() $\Pi_2\cup\Pi$
are equivalent for any program
$\Pi_2\cup\Pi$
are equivalent for any program
![]() $\Pi$
(Lifschitz et al. Reference Lifschitz, Pearce and Valverde2001). In particular, two rules
$\Pi$
(Lifschitz et al. Reference Lifschitz, Pearce and Valverde2001). In particular, two rules
![]() $r_1$
and
$r_1$
and
![]() $r_2$
are strongly equivalent if
$r_2$
are strongly equivalent if
![]() $\Pi\cup\{r_1\}$
and
$\Pi\cup\{r_1\}$
and
![]() $\Pi\cup\{r_2\}$
are equivalent for any program
$\Pi\cup\{r_2\}$
are equivalent for any program
![]() $\Pi$
.
$\Pi$
.
An answer set of a GEDP is not always minimal, that is, a program
![]() $\Pi$
may have two answer sets S and T such that
$\Pi$
may have two answer sets S and T such that
![]() $S\subset T$
. This is in contrast with the case of EDPs where every answer set is minimal.
$S\subset T$
. This is in contrast with the case of EDPs where every answer set is minimal.
Example 2.2 Let
![]() $\Pi$
be the program:
$\Pi$
be the program:
Then,
![]() $\Pi$
has two answer sets
$\Pi$
has two answer sets
![]() ${\varnothing}$
and
${\varnothing}$
and
![]() $\{p,q\}$
.
$\{p,q\}$
.
By definition, a contradictory GEDP has exactly one answer set Lit, while a consistent GEDP may have the answer set Lit.
Example 2.3 Let
![]() $\Pi$
be the program:
$\Pi$
be the program:
Then
![]() $\Pi$
has two answer sets
$\Pi$
has two answer sets
![]() ${\varnothing}$
and Lit.
${\varnothing}$
and Lit.
In EDPs, on the other hand, no consistent program has the answer set Lit, and every contradictory program has exactly one answer set Lit (Gelfond and Lifschitz Reference Gelfond and Lifschitz1991).
Suppose a rule r such that
![]() $head^+(r)={\varnothing}$
:
$head^+(r)={\varnothing}$
:
Define a rule
![]() $\eta(r)$
of the form:
$\eta(r)$
of the form:
that is obtained by shifting “
![]() $not\,L_{k+1}\,;\cdots ;\,not\,L_l $
" in
$not\,L_{k+1}\,;\cdots ;\,not\,L_l $
" in
![]() $head^-(r)$
to “
$head^-(r)$
to “
![]() $L_{k+1},\,\ldots,\,L_l$
" in
$L_{k+1},\,\ldots,\,L_l$
" in
![]() $body^+(\eta(r))$
. The two rules (3) and (4) are strongly equivalent under the answer set semantics.
$body^+(\eta(r))$
. The two rules (3) and (4) are strongly equivalent under the answer set semantics.
Proposition 2.1 (Inoue and Sakama Reference Inoue and Sakama1998)
Let
![]() $\Pi$
be a program and
$\Pi$
be a program and
![]() $\Phi=\{\,r\mid r\in\Pi\;\;\mbox{and}\;\; head^+(r)={\varnothing}\}$
. Also let
$\Phi=\{\,r\mid r\in\Pi\;\;\mbox{and}\;\; head^+(r)={\varnothing}\}$
. Also let
![]() $\Pi'=(\Pi\setminus \Phi)\cup \{\, \eta(r)\mid r\in\Phi\,\}$
. Then
$\Pi'=(\Pi\setminus \Phi)\cup \{\, \eta(r)\mid r\in\Phi\,\}$
. Then
![]() $\Pi$
and
$\Pi$
and
![]() $\Pi'$
have the same answer sets.
$\Pi'$
have the same answer sets.
Proposition 2.2 Let
![]() $\Pi$
be a program and
$\Pi$
be a program and
![]() $\Psi=\{\,r\mid r\in\Pi,\; head^+(r)={\varnothing}\;\mbox{and}\; head^-(r)\cap body^-(r)\neq{\varnothing}\}$
. Then,
$\Psi=\{\,r\mid r\in\Pi,\; head^+(r)={\varnothing}\;\mbox{and}\; head^-(r)\cap body^-(r)\neq{\varnothing}\}$
. Then,
![]() $\Pi$
and
$\Pi$
and
![]() $\Pi\setminus\Psi$
have the same answer sets.
$\Pi\setminus\Psi$
have the same answer sets.
Proof. By Proposition 2.1, every rule (3) in
![]() $\Pi$
is transformed to a strongly equivalent constraint (4). When
$\Pi$
is transformed to a strongly equivalent constraint (4). When
![]() $head^-(r)\cap body^-(r)\neq{\varnothing}$
for some
$head^-(r)\cap body^-(r)\neq{\varnothing}$
for some
![]() $r\in\Phi$
,
$r\in\Phi$
,
![]() $\{ L_{k+1},\ldots,L_l\}\cap \{L_{m+1},\ldots,L_n\}\neq{\varnothing}$
in
$\{ L_{k+1},\ldots,L_l\}\cap \{L_{m+1},\ldots,L_n\}\neq{\varnothing}$
in
![]() $\eta(r)$
of the form (4). Then,
$\eta(r)$
of the form (4). Then,
![]() $\{ L_{k+1},\ldots,L_l\}\subseteq S$
implies
$\{ L_{k+1},\ldots,L_l\}\subseteq S$
implies
![]() $\{L_{m+1},\ldots,L_n\}\cap S\neq{\varnothing}$
for any set S, and the constraint
$\{L_{m+1},\ldots,L_n\}\cap S\neq{\varnothing}$
for any set S, and the constraint
![]() $\eta(r)$
is satisfied by any answer set. Hence,
$\eta(r)$
is satisfied by any answer set. Hence,
![]() $\Psi$
is removed from
$\Psi$
is removed from
![]() $\Pi$
and the result follows.
$\Pi$
and the result follows.
Example 2.4 For any program
![]() $\Pi$
,
$\Pi$
,
is equivalent to the following program (Proposition 2.1):
which is further simplified to
![]() $\Pi$
(Proposition 2.2).
$\Pi$
(Proposition 2.2).
Proposition 2.3 Let
![]() $\Pi$
be a not-free GEDP. If there is a constraint in
$\Pi$
be a not-free GEDP. If there is a constraint in
![]() $\Pi$
, then
$\Pi$
, then
![]() $\Pi$
is not contradictory.
$\Pi$
is not contradictory.
Proof. If there is a constraint “
![]() $\leftarrow L_1,\ldots,L_m$
" in
$\leftarrow L_1,\ldots,L_m$
" in
![]() $\Pi$
, it is included in
$\Pi$
, it is included in
![]() $\Pi^{Lit}$
. Since Lit does not satisfy the constraint, it does not become the answer set of
$\Pi^{Lit}$
. Since Lit does not satisfy the constraint, it does not become the answer set of
![]() $\Pi^{Lit}$
. Hence,
$\Pi^{Lit}$
. Hence,
![]() $\Pi$
is not contradictory.
$\Pi$
is not contradictory.
3 Human conditional reasoning in ASP
ASP computes answer sets by deduction that is reasoning by AA. In this section, we present methods for reasoning by AC, DC, and DA in ASP.
3.1 AC completion
We first introduce a framework for reasoning by affirming the consequent (AC) in ASP. In GEDPs, a conditional sentence “
![]() ${\varphi}\Rightarrow \psi$
" ( if
${\varphi}\Rightarrow \psi$
" ( if
![]() ${\varphi}$
then
${\varphi}$
then
![]() $\psi$
) is represented by the rule “
$\psi$
) is represented by the rule “
![]() $\psi~\leftarrow~{\varphi}$
" where
$\psi~\leftarrow~{\varphi}$
" where
![]() $\psi$
is a disjunction “
$\psi$
is a disjunction “
![]() $L_1\,;\,\cdots\,;\, L_k\, ;\, not\,L_{k+1}\,;\cdots ;\,not\,L_l$
" and
$L_1\,;\,\cdots\,;\, L_k\, ;\, not\,L_{k+1}\,;\cdots ;\,not\,L_l$
" and
![]() ${\varphi}$
is a conjunction “
${\varphi}$
is a conjunction “
![]() $L_{l+1},\,\ldots,\,L_m,\,not\,L_{m+1},\,\ldots,\,not\,L_n$
". To realize reasoning backward from
$L_{l+1},\,\ldots,\,L_m,\,not\,L_{m+1},\,\ldots,\,not\,L_n$
". To realize reasoning backward from
![]() $\psi$
to
$\psi$
to
![]() ${\varphi}$
, we extend a program
${\varphi}$
, we extend a program
![]() $\Pi$
by introducing new rules.
$\Pi$
by introducing new rules.
Definition 3.1 (AC completion) Let
![]() $\Pi$
be a program and
$\Pi$
be a program and
![]() $r\in\Pi$
a rule of the form:
$r\in\Pi$
a rule of the form:
1. For each disjunct in
 $head^+(r)$
and
$head^+(r)$
and
 $head^-(r)$
, converse the implication: (5)
$head^-(r)$
, converse the implication: (5) \begin{eqnarray}&& L_{l+1},\,\ldots,\,L_m,\, not\,L_{m+1},\,\ldots,\,not\,L_n \;\leftarrow\; L_j \;\;\; (1\leq j\leq k), \end{eqnarray}
\begin{eqnarray}&& L_{l+1},\,\ldots,\,L_m,\, not\,L_{m+1},\,\ldots,\,not\,L_n \;\leftarrow\; L_j \;\;\; (1\leq j\leq k), \end{eqnarray}
In (5) and (6), the conjunction “
![]() $L_{l+1},\,\ldots,\,L_m,\, not\,L_{m+1},\,\ldots,\,not\,L_n$
" appears on the left of “
$L_{l+1},\,\ldots,\,L_m,\, not\,L_{m+1},\,\ldots,\,not\,L_n$
" appears on the left of “
![]() $\leftarrow$
". The produced (5) (resp. (6)) is considered an abbreviation of the collection of
$\leftarrow$
". The produced (5) (resp. (6)) is considered an abbreviation of the collection of
![]() $(n-l)$
rules:
$(n-l)$
rules:
![]() $(L_{l+1}\leftarrow L_j),\ldots, (not\,L_n\leftarrow L_j)$
(resp.
$(L_{l+1}\leftarrow L_j),\ldots, (not\,L_n\leftarrow L_j)$
(resp.
![]() $(L_{l+1}\leftarrow not\,L_j),\ldots, (not\,L_n\leftarrow not\,L_j)$
)Footnote 3, hence we abuse the term “rule” and call (5) or (6) a rule. In particular, (5) is not produced if
$(L_{l+1}\leftarrow not\,L_j),\ldots, (not\,L_n\leftarrow not\,L_j)$
)Footnote 3, hence we abuse the term “rule” and call (5) or (6) a rule. In particular, (5) is not produced if
![]() $head^+(r)={\varnothing}$
or
$head^+(r)={\varnothing}$
or
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
, and (6) is not produced if
$body^{+}(r)=body^{-}(r)={\varnothing}$
, and (6) is not produced if
![]() $head^-(r)={\varnothing}$
or
$head^-(r)={\varnothing}$
or
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
. The set of all rules (5) and (6) is denoted as conv(r).
$body^{+}(r)=body^{-}(r)={\varnothing}$
. The set of all rules (5) and (6) is denoted as conv(r).
2. Define
where each \begin{eqnarray*}ac(\Pi)&\!=\!& \{\; \Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; \ell_j \;\mid\\&& \quad \Sigma_i\leftarrow \ell_j \;\, (1\le i\le p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\, conv(r)\, \}\end{eqnarray*}
\begin{eqnarray*}ac(\Pi)&\!=\!& \{\; \Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; \ell_j \;\mid\\&& \quad \Sigma_i\leftarrow \ell_j \;\, (1\le i\le p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\, conv(r)\, \}\end{eqnarray*}
 $\Sigma_i$
$\Sigma_i$
 $(1\le i\le p)$
is a conjunction of literals and NAF-literals, and
$(1\le i\le p)$
is a conjunction of literals and NAF-literals, and
 $\ell_j$
is either a literal
$\ell_j$
is either a literal
 $L_j$
$L_j$
 $(1\le j\le k)$
or an NAF-literal
$(1\le j\le k)$
or an NAF-literal
 $not\,L_j$
$not\,L_j$
 $(k+1\le j\le l)$
.
$(k+1\le j\le l)$
.3. The AC completion of
 $\Pi$
is defined as: (5) and (6) in conv(r) represent converse implications from the disjunction in the head of r to the conjunction in the body of r.
$\Pi$
is defined as: (5) and (6) in conv(r) represent converse implications from the disjunction in the head of r to the conjunction in the body of r. $$ AC(\Pi) = \Pi \;\cup\; ac(\Pi). $$
$$ AC(\Pi) = \Pi \;\cup\; ac(\Pi). $$
 $ac(\Pi)$
collects rules “
$ac(\Pi)$
collects rules “
 $\Sigma_i\leftarrow \ell_j$
"
$\Sigma_i\leftarrow \ell_j$
"
 $(1\le i\le p)$
having the same (NAF-)literal
$(1\le i\le p)$
having the same (NAF-)literal
 $\ell_j$
on the right of “
$\ell_j$
on the right of “
 $\leftarrow$
", and constructs “
$\leftarrow$
", and constructs “
 $\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; \ell_j$
," which we call an extended rule. Introducing
$\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; \ell_j$
," which we call an extended rule. Introducing
 $ac(\Pi)$
to
$ac(\Pi)$
to
 $\Pi$
realizes reasoning by AC in
$\Pi$
realizes reasoning by AC in
 $\Pi$
.
$\Pi$
.
The set
![]() $ac(\Pi)$
contains an extended rule having a disjunction of conjunctions in its head, while it is transformed to rules of a GEDP. That is, the extended rule:
$ac(\Pi)$
contains an extended rule having a disjunction of conjunctions in its head, while it is transformed to rules of a GEDP. That is, the extended rule:
is identified with the set of
![]() $(m_1\times\cdots\times m_p)$
rules of the form:
$(m_1\times\cdots\times m_p)$
rules of the form:
By this fact,
![]() $AC(\Pi)$
is viewed as a GEDP and we do not distinguish extended rules and rules of a GEDP hereafter. The semantics of
$AC(\Pi)$
is viewed as a GEDP and we do not distinguish extended rules and rules of a GEDP hereafter. The semantics of
![]() $AC(\Pi)$
is defined by its answer sets.
$AC(\Pi)$
is defined by its answer sets.
Example 3.1 Let
![]() $\Pi$
be the program:
$\Pi$
be the program:
Then,
![]() $ac(\Pi)$
becomes
$ac(\Pi)$
becomes
where the first rule “
![]() $(r,\, not\,s)\,;\, q\leftarrow p$
" is identified with
$(r,\, not\,s)\,;\, q\leftarrow p$
" is identified with
and the second rule “
![]() $r,\, not\,s\leftarrow not\,q$
" is identified with
$r,\, not\,s\leftarrow not\,q$
" is identified with
Then,
![]() $AC(\Pi)\cup \{p\leftarrow\}$
has two answer sets
$AC(\Pi)\cup \{p\leftarrow\}$
has two answer sets
![]() $\{p,q\}$
and
$\{p,q\}$
and
![]() $\{p,r\}$
.
$\{p,r\}$
.
By definition, if there is more than one rule in
![]() $\Pi$
having the same (NAF-)literal in the heads, they are collected to produce a single converse rule in
$\Pi$
having the same (NAF-)literal in the heads, they are collected to produce a single converse rule in
![]() $ac(\Pi)$
. For instance,
$ac(\Pi)$
. For instance,
![]() $\Pi=\{\, p\leftarrow~q,\;\; p\leftarrow~r\,\}$
produces
$\Pi=\{\, p\leftarrow~q,\;\; p\leftarrow~r\,\}$
produces
![]() $ac(\Pi)=\{\, q\,;\,r\leftarrow p\,\}$
but not
$ac(\Pi)=\{\, q\,;\,r\leftarrow p\,\}$
but not
![]() $\Lambda=\{\, q\leftarrow p,\;\; r\leftarrow p\,\}$
. Then,
$\Lambda=\{\, q\leftarrow p,\;\; r\leftarrow p\,\}$
. Then,
![]() $AC(\Pi)\cup\{ p\leftarrow\}$
has two answer sets
$AC(\Pi)\cup\{ p\leftarrow\}$
has two answer sets
![]() $\{p,q\}$
and
$\{p,q\}$
and
![]() $\{p,r\}$
. Suppose that the new fact “
$\{p,r\}$
. Suppose that the new fact “
![]() $\neg\, q\leftarrow$
" is added to
$\neg\, q\leftarrow$
" is added to
![]() $\Pi$
. Put
$\Pi$
. Put
![]() $\Pi'=\Pi\cup\{\,\neg\, q\leftarrow\,\}$
. Then,
$\Pi'=\Pi\cup\{\,\neg\, q\leftarrow\,\}$
. Then,
![]() $AC(\Pi')\cup\{ p\leftarrow\}$
has the answer set
$AC(\Pi')\cup\{ p\leftarrow\}$
has the answer set
![]() $\{p,r\}$
, which represents the result of AC reasoning in
$\{p,r\}$
, which represents the result of AC reasoning in
![]() $\Pi'$
. If
$\Pi'$
. If
![]() $\Lambda$
is used instead of
$\Lambda$
is used instead of
![]() $ac(\Pi)$
, however,
$ac(\Pi)$
, however,
![]() $\Pi'\cup\Lambda\cup\{ p\leftarrow\}$
has the answer set Lit. The result is too strong because r is consistently inferred from
$\Pi'\cup\Lambda\cup\{ p\leftarrow\}$
has the answer set Lit. The result is too strong because r is consistently inferred from
![]() $\Pi'\cup\{ p\leftarrow\}$
by AC reasoning. As a concrete example, put
$\Pi'\cup\{ p\leftarrow\}$
by AC reasoning. As a concrete example, put
![]() $p=wet\mbox{-}grass$
,
$p=wet\mbox{-}grass$
,
![]() $q=rain$
, and
$q=rain$
, and
![]() $r=sprinkler\mbox{-}on$
. Then,
$r=sprinkler\mbox{-}on$
. Then,
![]() $AC(\Pi')\cup\{wet\mbox{-}grass\leftarrow\,\}$
has the answer set
$AC(\Pi')\cup\{wet\mbox{-}grass\leftarrow\,\}$
has the answer set
![]() $\{\,wet\mbox{-}grass, \neg\, rain, sprinkler\mbox{-}on\,\}$
, while
$\{\,wet\mbox{-}grass, \neg\, rain, sprinkler\mbox{-}on\,\}$
, while
![]() $\Pi'\cup\Lambda\cup\{wet\mbox{-}grass\leftarrow\,\}$
has the answer set Lit. AC completion derives an antecedent from a consequent, but it does not derive negation of antecedent by its nature. For instance, given
$\Pi'\cup\Lambda\cup\{wet\mbox{-}grass\leftarrow\,\}$
has the answer set Lit. AC completion derives an antecedent from a consequent, but it does not derive negation of antecedent by its nature. For instance, given
![]() $\Pi=\{\, p\,;\,q\leftarrow r,\;\;\; p\leftarrow\,\}$
,
$\Pi=\{\, p\,;\,q\leftarrow r,\;\;\; p\leftarrow\,\}$
,
![]() $AC(\Pi)\models_s r$
but
$AC(\Pi)\models_s r$
but
![]() $AC(\Pi)\not\models_c \neg\,q$
.
$AC(\Pi)\not\models_c \neg\,q$
.
Note that in Definition 3.1, the converse of constraints and facts are not produced. When
![]() $head^+(r)=head^-(r)={\varnothing}$
, r is considered a rule with
$head^+(r)=head^-(r)={\varnothing}$
, r is considered a rule with
![]() $\mathit{false}$
in the head, then (5) and (6) become
$\mathit{false}$
in the head, then (5) and (6) become
which has no effect as a rule. On the other hand, when
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
, r is considered a rule with
$body^{+}(r)=body^{-}(r)={\varnothing}$
, r is considered a rule with
![]() $\mathit{true}$
in the body, then (5) and (6) respectively become
$\mathit{true}$
in the body, then (5) and (6) respectively become
We do not include this type of rules for constructing
![]() $ac(\Pi)$
because it would disable AC reasoning. For instance, transform
$ac(\Pi)$
because it would disable AC reasoning. For instance, transform
![]() $\Pi=\{\, p\leftarrow q,\;\;\; p\leftarrow\,\}$
to
$\Pi=\{\, p\leftarrow q,\;\;\; p\leftarrow\,\}$
to
![]() $\Pi'=\Pi\cup\{ q\,; true\leftarrow p\}$
. Then,
$\Pi'=\Pi\cup\{ q\,; true\leftarrow p\}$
. Then,
![]() $\{p\}$
is the minimal set satisfying
$\{p\}$
is the minimal set satisfying
![]() $\Pi'$
, and q is not included in the answer set of
$\Pi'$
, and q is not included in the answer set of
![]() $\Pi'$
. With this reason, constraints and facts are not completed at the first step of Definition 3.1.
$\Pi'$
. With this reason, constraints and facts are not completed at the first step of Definition 3.1.
The result of AC completion is syntax-dependent in general. That is, two (strongly) equivalent programs may produce different AC completions.
Example 3.2 Let
![]() $\Pi_1=\{\, not\,p\leftarrow q\,\}$
and
$\Pi_1=\{\, not\,p\leftarrow q\,\}$
and
![]() $\Pi_2=\{\, \leftarrow p,q \,\}$
. By Proposition 2.1,
$\Pi_2=\{\, \leftarrow p,q \,\}$
. By Proposition 2.1,
![]() $\Pi_1$
and
$\Pi_1$
and
![]() $\Pi_2$
are equivalent, but
$\Pi_2$
are equivalent, but
![]() $AC(\Pi_1)=\Pi_1\cup \{\, q\leftarrow not\,p\,\}$
and
$AC(\Pi_1)=\Pi_1\cup \{\, q\leftarrow not\,p\,\}$
and
![]() $AC(\Pi_2)=\Pi_2$
. As a result,
$AC(\Pi_2)=\Pi_2$
. As a result,
![]() $AC(\Pi_1)$
has the answer set
$AC(\Pi_1)$
has the answer set
![]() $\{q\}$
while
$\{q\}$
while
![]() $AC(\Pi_2)$
has the answer set
$AC(\Pi_2)$
has the answer set
![]() ${\varnothing}$
.
${\varnothing}$
.
In the above example, “
![]() $not\,p\leftarrow q$
” is a conditional sentence which is subject to AC inference, while “
$not\,p\leftarrow q$
” is a conditional sentence which is subject to AC inference, while “
![]() $\leftarrow p,q$
” is a constraint which is not subject to AC inference by definition. For instance, given the conditional sentence “if it is sunny, the grass is not wet" and the fact “the grass is not wet.," people would infer “it is sunny" by AC inference. On the other hand, given the constraint “it does not happen that wet-grass and sunny-weather at the same time" and the fact “the grass is not wet," the number of people who infer “it is sunny" by AC would be smaller because the cause-effect relation between “sunny" and “not wet" is not explicitly expressed in the constraint.
$\leftarrow p,q$
” is a constraint which is not subject to AC inference by definition. For instance, given the conditional sentence “if it is sunny, the grass is not wet" and the fact “the grass is not wet.," people would infer “it is sunny" by AC inference. On the other hand, given the constraint “it does not happen that wet-grass and sunny-weather at the same time" and the fact “the grass is not wet," the number of people who infer “it is sunny" by AC would be smaller because the cause-effect relation between “sunny" and “not wet" is not explicitly expressed in the constraint.
Reasoning by AC is nonmonotonic in the sense that
![]() $\Pi\models_c L$
(or
$\Pi\models_c L$
(or
![]() $\Pi\models_s L$
) does not imply
$\Pi\models_s L$
) does not imply
![]() $AC(\Pi)\models_c L$
(or
$AC(\Pi)\models_c L$
(or
![]() $AC(\Pi)\models_s L$
) in general.
$AC(\Pi)\models_s L$
) in general.
Example 3.3 The program
![]() $\Pi=\{\, p\leftarrow not\,q,\;\; r\leftarrow q,\;\; r\leftarrow \,\}$
has the answer set
$\Pi=\{\, p\leftarrow not\,q,\;\; r\leftarrow q,\;\; r\leftarrow \,\}$
has the answer set
![]() $\{p,r\}$
, while
$\{p,r\}$
, while
![]() $AC(\Pi)=\Pi\cup\{\, not\,q\leftarrow p,\;\; q\leftarrow r\,\}$
has the answer set
$AC(\Pi)=\Pi\cup\{\, not\,q\leftarrow p,\;\; q\leftarrow r\,\}$
has the answer set
![]() $\{q,r\}$
.
$\{q,r\}$
.
In Example 3.3, reasoning by AC produces q which blocks deriving p using the first rule in
![]() $\Pi$
. As a concrete example, an online-meeting is held on time if no network trouble arises. However, it turns that the web browser is unconnected and one suspects that there is some trouble on the network. Put p=“online-meeting is held on time," q=“network trouble," r=“the web browser is unconnected." In this case, one may withdraw the conclusion p after knowing r. As such, additional rules
$\Pi$
. As a concrete example, an online-meeting is held on time if no network trouble arises. However, it turns that the web browser is unconnected and one suspects that there is some trouble on the network. Put p=“online-meeting is held on time," q=“network trouble," r=“the web browser is unconnected." In this case, one may withdraw the conclusion p after knowing r. As such, additional rules
![]() $ac(\Pi)$
may change the results of
$ac(\Pi)$
may change the results of
![]() $\Pi$
. One can see the effect of AC reasoning in a program
$\Pi$
. One can see the effect of AC reasoning in a program
![]() $\Pi$
by comparing answer sets of
$\Pi$
by comparing answer sets of
![]() $\Pi$
and
$\Pi$
and
![]() $AC(\Pi)$
.
$AC(\Pi)$
.
A consistent program
![]() $\Pi$
may produce an inconsistent
$\Pi$
may produce an inconsistent
![]() $AC(\Pi)$
. In converse, an inconsistent
$AC(\Pi)$
. In converse, an inconsistent
![]() $\Pi$
may produce a consistent
$\Pi$
may produce a consistent
![]() $AC(\Pi)$
.
$AC(\Pi)$
.
Example 3.4
![]() $\Pi_1=\{\, p\leftarrow \neg\, p,\;\;\; p\leftarrow\,\}$
is consistent, but
$\Pi_1=\{\, p\leftarrow \neg\, p,\;\;\; p\leftarrow\,\}$
is consistent, but
![]() $AC(\Pi_1)=\Pi_1\cup \{\, \neg\,p\leftarrow p\,\}$
is contradictory.
$AC(\Pi_1)=\Pi_1\cup \{\, \neg\,p\leftarrow p\,\}$
is contradictory.
![]() $\Pi_2=\{\, \leftarrow not\,p,\;\;\; q\leftarrow p,\;\;\; q\leftarrow\,\}$
is incoherent, but
$\Pi_2=\{\, \leftarrow not\,p,\;\;\; q\leftarrow p,\;\;\; q\leftarrow\,\}$
is incoherent, but
![]() $AC(\Pi_2)=\Pi_2\cup \{\, p\leftarrow q\,\}$
is consistent.
$AC(\Pi_2)=\Pi_2\cup \{\, p\leftarrow q\,\}$
is consistent.
A sufficient condition for the consistency of
![]() $AC(\Pi)$
is given below.
$AC(\Pi)$
is given below.
Proposition 3.1 If a PDP
![]() $\Pi$
contains no constraint, then
$\Pi$
contains no constraint, then
![]() $AC(\Pi)$
is consistent. Moreover, for any answer set S of
$AC(\Pi)$
is consistent. Moreover, for any answer set S of
![]() $\Pi$
, there is an answer set T of
$\Pi$
, there is an answer set T of
![]() $AC(\Pi)$
such that
$AC(\Pi)$
such that
![]() $S\subseteq T$
.
$S\subseteq T$
.
Proof. A PDP
![]() $\Pi$
contains no NAF-literal and every literal in
$\Pi$
contains no NAF-literal and every literal in
![]() $\Pi$
is a positive literal (or an atom). Then,
$\Pi$
is a positive literal (or an atom). Then,
![]() $ac(\Pi)$
is the set of rules
$ac(\Pi)$
is the set of rules
![]() $(\Sigma_1;\cdots;\Sigma_p\leftarrow A_j)$
where
$(\Sigma_1;\cdots;\Sigma_p\leftarrow A_j)$
where
![]() $A_j$
is an atom and
$A_j$
is an atom and
![]() $\Sigma_i$
is a conjunction of atoms. When
$\Sigma_i$
is a conjunction of atoms. When
![]() $\Pi$
contains no constraint, the additional rules in
$\Pi$
contains no constraint, the additional rules in
![]() $ac(\Pi)$
do not cause inconsistency in
$ac(\Pi)$
do not cause inconsistency in
![]() $AC(\Pi)=\Pi\cup ac(\Pi)$
. Suppose that S is an answer set (or a minimal model) of
$AC(\Pi)=\Pi\cup ac(\Pi)$
. Suppose that S is an answer set (or a minimal model) of
![]() $\Pi$
. Then S is a minimal set satisfying all rules in
$\Pi$
. Then S is a minimal set satisfying all rules in
![]() $\Pi$
. Let
$\Pi$
. Let
![]() $U=\{\, A\, \mid\, A\in head^+(r)\;\mbox{for any rule}\; r\in ac(\Pi)\;\mbox{such that}\; body^+(r)\subseteq S\,\}$
. Then, there is an answer set T of
$U=\{\, A\, \mid\, A\in head^+(r)\;\mbox{for any rule}\; r\in ac(\Pi)\;\mbox{such that}\; body^+(r)\subseteq S\,\}$
. Then, there is an answer set T of
![]() $AC(\Pi)$
such that
$AC(\Pi)$
such that
![]() $T=S\cup V$
where
$T=S\cup V$
where
![]() $V\subseteq U$
. Hence, the result holds.
$V\subseteq U$
. Hence, the result holds.
Proposition 3.2 If a program
![]() $\Pi$
has the answer set Lit, then
$\Pi$
has the answer set Lit, then
![]() $AC(\Pi)$
has the answer set Lit.
$AC(\Pi)$
has the answer set Lit.
Proof. If
![]() $\Pi$
has the answer set Lit, the reduct
$\Pi$
has the answer set Lit, the reduct
![]() $\Pi^{Lit}$
has the answer set Lit. By definition,
$\Pi^{Lit}$
has the answer set Lit. By definition,
![]() $AC(\Pi)^{Lit}=\Pi^{Lit} \cup ac(\Pi)^{Lit}$
where
$AC(\Pi)^{Lit}=\Pi^{Lit} \cup ac(\Pi)^{Lit}$
where
![]() $ac(\Pi)^{Lit}$
is the reduct of
$ac(\Pi)^{Lit}$
is the reduct of
![]() $ac(\Pi)$
by Lit. Introducing not-free rules in
$ac(\Pi)$
by Lit. Introducing not-free rules in
![]() $ac(\Pi)^{Lit}$
does not change the answer set Lit of
$ac(\Pi)^{Lit}$
does not change the answer set Lit of
![]() $\Pi^{Lit}$
. Then, Lit is the answer set of
$\Pi^{Lit}$
. Then, Lit is the answer set of
![]() $AC(\Pi)^{Lit}$
and the result follows.
$AC(\Pi)^{Lit}$
and the result follows.
3.2 DC completion
We next introduce a framework for reasoning by denying the consequent (DC) in ASP. There are two ways for negating a literal – one is using explicit negation and the other is using default negation. Accordingly, there are two ways of completing a program for the purpose of reasoning by DC.
Definition 3.2 (DC completion) Let
![]() $\Pi$
be a program. For each rule
$\Pi$
be a program. For each rule
![]() $r\in\Pi$
of the form:
$r\in\Pi$
of the form:
define wdc(r) as the rule:
and define sdc(r) as the rule:
In particular, (7) or (8) becomes a fact if
![]() $head^+(r)=head^-(r)={\varnothing}$
, and it becomes a constraint if
$head^+(r)=head^-(r)={\varnothing}$
, and it becomes a constraint if
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
. The weak DC completion and the strong DC completion of
$body^{+}(r)=body^{-}(r)={\varnothing}$
. The weak DC completion and the strong DC completion of
![]() $\Pi$
are respectively defined as:
$\Pi$
are respectively defined as:
By definition,
![]() $WDC(\Pi)$
and
$WDC(\Pi)$
and
![]() $SDC(\Pi)$
introduce contrapositive rules in two different ways. In (7), literals
$SDC(\Pi)$
introduce contrapositive rules in two different ways. In (7), literals
![]() $L_i$
$L_i$
![]() $(1\leq i\leq k;\,l+1\leq i\leq m)$
are negated using default negation not and NAF-literals
$(1\leq i\leq k;\,l+1\leq i\leq m)$
are negated using default negation not and NAF-literals
![]() $not\,L_j$
$not\,L_j$
![]() $(k+1\leq i\leq l;\,m+1\leq i\leq n)$
are converted to
$(k+1\leq i\leq l;\,m+1\leq i\leq n)$
are converted to
![]() $L_j$
. In (8), on the other hand, literals
$L_j$
. In (8), on the other hand, literals
![]() $L_i$
$L_i$
![]() $(1\leq i\leq k;\,l+1\leq i\leq m)$
are negated using explicit negation
$(1\leq i\leq k;\,l+1\leq i\leq m)$
are negated using explicit negation
![]() $\neg$
and NAF-literals
$\neg$
and NAF-literals
![]() $not\,L_j$
$not\,L_j$
![]() $(k+1\leq i\leq l;\,m+1\leq i\leq n)$
are converted to
$(k+1\leq i\leq l;\,m+1\leq i\leq n)$
are converted to
![]() $L_j$
.
$L_j$
.
![]() $WDC(\Pi)$
and
$WDC(\Pi)$
and
![]() $SDC(\Pi)$
are GEDPs, and their semantics are defined by their answer sets. In particular,
$SDC(\Pi)$
are GEDPs, and their semantics are defined by their answer sets. In particular,
![]() $SDC(\Pi)$
becomes an EDP if
$SDC(\Pi)$
becomes an EDP if
![]() $\Pi$
is an EDP.
$\Pi$
is an EDP.
Note that contraposition of facts or constraints is produced in WDC/SDC. For instance, the fact “
![]() $p\leftarrow$
" produces the constraint “
$p\leftarrow$
" produces the constraint “
![]() $\leftarrow not\,p$
" by WDC and “
$\leftarrow not\,p$
" by WDC and “
![]() $\leftarrow \neg p$
" by SDC. The fact “
$\leftarrow \neg p$
" by SDC. The fact “
![]() $not\,p\leftarrow$
" produces the constraint “
$not\,p\leftarrow$
" produces the constraint “
![]() $\leftarrow p$
" by WDC and SDC. On the other side, the constraint “
$\leftarrow p$
" by WDC and SDC. On the other side, the constraint “
![]() $\leftarrow p$
" produces the fact “
$\leftarrow p$
" produces the fact “
![]() $not\,p\leftarrow$
" by WDC and “
$not\,p\leftarrow$
" by WDC and “
![]() $\neg p\leftarrow$
" by SDC. The constraint “
$\neg p\leftarrow$
" by SDC. The constraint “
![]() $\leftarrow not\,p$
" produces the fact “
$\leftarrow not\,p$
" produces the fact “
![]() $p\leftarrow$
" by WDC and SDC.
$p\leftarrow$
" by WDC and SDC.
The WDC and SDC produce different results in general.
Example 3.5 Given
![]() $\Pi=\{\,p\leftarrow not\, q\,\}$
, it becomes
$\Pi=\{\,p\leftarrow not\, q\,\}$
, it becomes
Then,
![]() $WDC(\Pi)$
has two answer sets
$WDC(\Pi)$
has two answer sets
![]() $\{p\}$
and
$\{p\}$
and
![]() $\{q\}$
, while
$\{q\}$
, while
![]() $SDC(\Pi)$
has the single answer set
$SDC(\Pi)$
has the single answer set
![]() $\{ p\}$
.
$\{ p\}$
.
Example 3.5 shows that WDC is nonmonotonic as
![]() $\Pi\models_s p$
but
$\Pi\models_s p$
but
![]() $WDC(\Pi)\not\models_s p$
. SDC is also nonmonotonic (see Example 3.8). The result of DC completion is syntax-dependent in general.
$WDC(\Pi)\not\models_s p$
. SDC is also nonmonotonic (see Example 3.8). The result of DC completion is syntax-dependent in general.
Example 3.6 Let
![]() $\Pi_1=\{\, not\,p\leftarrow q\,\}$
and
$\Pi_1=\{\, not\,p\leftarrow q\,\}$
and
![]() $\Pi_2=\{\, \leftarrow p,q \,\}$
where
$\Pi_2=\{\, \leftarrow p,q \,\}$
where
![]() $\Pi_1$
and
$\Pi_1$
and
![]() $\Pi_2$
are equivalent (Proposition 2.1). Then,
$\Pi_2$
are equivalent (Proposition 2.1). Then,
![]() $SDC(\Pi_1)=\Pi_1\cup \{\, \neg\,q\leftarrow p\,\}$
and
$SDC(\Pi_1)=\Pi_1\cup \{\, \neg\,q\leftarrow p\,\}$
and
![]() $SDC(\Pi_2)=\Pi_2\cup\{\,\neg\,p\,; \neg\,q\leftarrow\,\}$
. As a result,
$SDC(\Pi_2)=\Pi_2\cup\{\,\neg\,p\,; \neg\,q\leftarrow\,\}$
. As a result,
![]() $SDC(\Pi_1)$
has the answer set
$SDC(\Pi_1)$
has the answer set
![]() ${\varnothing}$
, while
${\varnothing}$
, while
![]() $SDC(\Pi_2)$
has two answer sets
$SDC(\Pi_2)$
has two answer sets
![]() $\{\neg\,p\}$
and
$\{\neg\,p\}$
and
![]() $\{\neg\,q\}$
.
$\{\neg\,q\}$
.
WDC preserves the consistency of the original program.
Proposition 3.3 If a program
![]() $\Pi$
has a consistent answer set S, then S is an answer set of
$\Pi$
has a consistent answer set S, then S is an answer set of
![]() $WDC(\Pi)$
.
$WDC(\Pi)$
.
Proof. Suppose a consistent answer set S of
![]() $\Pi$
. Then, for any rule (
$\Pi$
. Then, for any rule (
![]() $L_1\, ;\,\cdots\, ;\, L_k \leftarrow L_{l+1},\,\ldots,\,L_m$
) in
$L_1\, ;\,\cdots\, ;\, L_k \leftarrow L_{l+1},\,\ldots,\,L_m$
) in
![]() $\Pi^S$
, either
$\Pi^S$
, either
![]() $\{L_1,\ldots,L_k\}\cap S\neq{\varnothing}$
or
$\{L_1,\ldots,L_k\}\cap S\neq{\varnothing}$
or
![]() $\{L_{l+1},\ldots,L_m\}\not\subseteq S$
. In each case, the rule (7) is eliminated in
$\{L_{l+1},\ldots,L_m\}\not\subseteq S$
. In each case, the rule (7) is eliminated in
![]() $\Pi^S$
. Then, S is an answer set of
$\Pi^S$
. Then, S is an answer set of
![]() $WDC(\Pi)^S$
; hence, the result holds.
$WDC(\Pi)^S$
; hence, the result holds.
The converse of Proposition 3.3 does not hold in general.
Example 3.7 The program
![]() $\Pi=\{\, \leftarrow not\,p \,\}$
has no answer set, while
$\Pi=\{\, \leftarrow not\,p \,\}$
has no answer set, while
![]() $WDC(\Pi)=\{\, \leftarrow~not\,p,\;\; p\leftarrow \,\}$
has the answer set
$WDC(\Pi)=\{\, \leftarrow~not\,p,\;\; p\leftarrow \,\}$
has the answer set
![]() $\{p\}$
.
$\{p\}$
.
For
![]() $SDC(\Pi)$
, the next result holds.
$SDC(\Pi)$
, the next result holds.
Proposition 3.4 Let
![]() $\Pi$
be a consistent program such that every constraint in
$\Pi$
be a consistent program such that every constraint in
![]() $\Pi$
is not-free (i.e.
$\Pi$
is not-free (i.e.
![]() $head^+(r)=head^-(r)={\varnothing}$
implies
$head^+(r)=head^-(r)={\varnothing}$
implies
![]() $body^-(r)={\varnothing}$
for any
$body^-(r)={\varnothing}$
for any
![]() $r\in\Pi$
). Then,
$r\in\Pi$
). Then,
![]() $SDC(\Pi)$
does not have the answer set Lit.
$SDC(\Pi)$
does not have the answer set Lit.
Proof. Consider
![]() $SDC(\Pi)^{Lit}=(\Pi \;\cup\; \{sdc(r) \,\mid\, r\in \Pi \,\})^{Lit}=\Pi^{Lit}\;\cup\; \{sdc(r) \,\mid\, r\in \Pi \,\}$
.
$SDC(\Pi)^{Lit}=(\Pi \;\cup\; \{sdc(r) \,\mid\, r\in \Pi \,\})^{Lit}=\Pi^{Lit}\;\cup\; \{sdc(r) \,\mid\, r\in \Pi \,\}$
.
(a) If there is a constraint
![]() $r\in \Pi$
such that
$r\in \Pi$
such that
![]() $head^+(r)=head^-(r)={\varnothing}$
, then
$head^+(r)=head^-(r)={\varnothing}$
, then
![]() $body^-(r)={\varnothing}$
by the assumption. Then,
$body^-(r)={\varnothing}$
by the assumption. Then,
![]() $r\in\Pi^{Lit}$
and
$r\in\Pi^{Lit}$
and
![]() $SDC(\Pi)^{Lit}$
does not have the answer set Lit (Proposition 2.3). (b) Else if there is no constraint in
$SDC(\Pi)^{Lit}$
does not have the answer set Lit (Proposition 2.3). (b) Else if there is no constraint in
![]() $\Pi$
, then
$\Pi$
, then
![]() $\{sdc(r) \,\mid\, r\in \Pi \,\}$
contains no fact by Definition 3.2. Consider two cases. (i) When there is a fact
$\{sdc(r) \,\mid\, r\in \Pi \,\}$
contains no fact by Definition 3.2. Consider two cases. (i) When there is a fact
![]() $r\in\Pi$
, sdc(r) becomes a not-free constraint by Definition 3.2. As
$r\in\Pi$
, sdc(r) becomes a not-free constraint by Definition 3.2. As
![]() $SDC(\Pi)^{Lit}$
contains this constraint, it does not have the answer set Lit (Proposition 2.3). (ii) When there is no fact in
$SDC(\Pi)^{Lit}$
contains this constraint, it does not have the answer set Lit (Proposition 2.3). (ii) When there is no fact in
![]() $\Pi$
, both
$\Pi$
, both
![]() $\Pi^{Lit}$
and
$\Pi^{Lit}$
and
![]() $\{sdc(r) \,\mid\, r\in \Pi \,\}$
contain no fact, so
$\{sdc(r) \,\mid\, r\in \Pi \,\}$
contain no fact, so
![]() $SDC(\Pi)^{Lit}$
contains no fact. In this case, no literal is deduced in
$SDC(\Pi)^{Lit}$
contains no fact. In this case, no literal is deduced in
![]() $SDC(\Pi)^{Lit}$
and it does not have the answer set Lit. By (a) and (b),
$SDC(\Pi)^{Lit}$
and it does not have the answer set Lit. By (a) and (b),
![]() $SDC(\Pi)^{Lit}$
does not have the answer set Lit. Hence, the result follows.
$SDC(\Pi)^{Lit}$
does not have the answer set Lit. Hence, the result follows.
A program
![]() $\Pi$
satisfying the condition of Proposition 3.4 may produce an incoherent
$\Pi$
satisfying the condition of Proposition 3.4 may produce an incoherent
![]() $SDC(\Pi)$
.
$SDC(\Pi)$
.
Example 3.8 The program
![]() $\Pi = \{\, p\leftarrow q,\;\;\; p\leftarrow \neg q,\;\;\; \neg\,p\leftarrow\, \}$
has the answer set
$\Pi = \{\, p\leftarrow q,\;\;\; p\leftarrow \neg q,\;\;\; \neg\,p\leftarrow\, \}$
has the answer set
![]() $\{\neg\,p\}$
, but
$\{\neg\,p\}$
, but
is incoherent.
Proposition 3.5 If a program
![]() $\Pi$
has the answer set Lit, then both
$\Pi$
has the answer set Lit, then both
![]() $WDC(\Pi)$
and
$WDC(\Pi)$
and
![]() $SDC(\Pi)$
have the answer set Lit. In particular, if
$SDC(\Pi)$
have the answer set Lit. In particular, if
![]() $\Pi$
is a contradictory EDP, then
$\Pi$
is a contradictory EDP, then
![]() $SDC(\Pi)$
is contradictory.
$SDC(\Pi)$
is contradictory.
Proof. The proof is similar to Proposition 3.2. In particular, if
![]() $\Pi$
is an EDP, then
$\Pi$
is an EDP, then
![]() $SDC(\Pi)$
is an EDP and the result holds.
$SDC(\Pi)$
is an EDP and the result holds.
Note that in GEDPs, contraposition of a rule does not hold in general. Thus, the program
![]() $\Pi=\{\, p\leftarrow q,\;\; \neg\,p\leftarrow \,\}$
does not deduce
$\Pi=\{\, p\leftarrow q,\;\; \neg\,p\leftarrow \,\}$
does not deduce
![]() $\neg\,q$
. SDC completes the program as
$\neg\,q$
. SDC completes the program as
![]() $SDC(\Pi)=\Pi\cup \{\, \neg\,q\leftarrow \neg\,p,\;\; \leftarrow p\,\}$
and makes
$SDC(\Pi)=\Pi\cup \{\, \neg\,q\leftarrow \neg\,p,\;\; \leftarrow p\,\}$
and makes
![]() $\neg\,q$
deducible. In this sense, SDC has the effect of making explicit negation closer to classical negation in GEDP.
$\neg\,q$
deducible. In this sense, SDC has the effect of making explicit negation closer to classical negation in GEDP.
3.3 DA completion
As a third extension, we introduce a framework for reasoning by denying the antecedent (DA) in ASP. As in the case of DC completion, two different ways of completion are considered depending on the choice of negation.
Definition 3.3 (weak DA completion) Let
![]() $\Pi$
be a program and
$\Pi$
be a program and
![]() $r\in\Pi$
a rule of the form:
$r\in\Pi$
a rule of the form:
1. For each disjunct in
 $head^+(r)$
and
$head^+(r)$
and
 $head^-(r)$
, inverse the implication: (9)
$head^-(r)$
, inverse the implication: (9) \begin{eqnarray}not\,L_i &\leftarrow& not\,L_{l+1}\,;\,\cdots\, ;\, not\,L_m\,;\, L_{m+1}\,;\cdots\, ;\, L_n\;\; (1\leq i\leq k), \end{eqnarray}
\begin{eqnarray}not\,L_i &\leftarrow& not\,L_{l+1}\,;\,\cdots\, ;\, not\,L_m\,;\, L_{m+1}\,;\cdots\, ;\, L_n\;\; (1\leq i\leq k), \end{eqnarray}
In (9) and (10), the disjunction “
![]() $not\,L_{l+1}\,;\,\cdots\, ;\, not\,L_m\,;\, L_{m+1}\,;\,\cdots\, ;\, L_n$
" appears on the right of “
$not\,L_{l+1}\,;\,\cdots\, ;\, not\,L_m\,;\, L_{m+1}\,;\,\cdots\, ;\, L_n$
" appears on the right of “
![]() $\leftarrow$
". The produced (9) (resp. (10)) is considered an abbreviation of the collection of
$\leftarrow$
". The produced (9) (resp. (10)) is considered an abbreviation of the collection of
![]() $(n-l)$
rules:
$(n-l)$
rules:
![]() $(not\,L_i \leftarrow not\,L_{l+1}),\ldots, (not\,L_i \leftarrow L_n)$
(resp.
$(not\,L_i \leftarrow not\,L_{l+1}),\ldots, (not\,L_i \leftarrow L_n)$
(resp.
![]() $(L_i \leftarrow not\,L_{l+1}),\ldots, (L_i \leftarrow L_n)$
), hence we abuse the term “rule” and call (9) or (10) a rule. In particular, (9) is not produced if
$(L_i \leftarrow not\,L_{l+1}),\ldots, (L_i \leftarrow L_n)$
), hence we abuse the term “rule” and call (9) or (10) a rule. In particular, (9) is not produced if
![]() $head^+(r)={\varnothing}$
or
$head^+(r)={\varnothing}$
or
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
, and (10) is not produced if
$body^{+}(r)=body^{-}(r)={\varnothing}$
, and (10) is not produced if
![]() $head^-(r)={\varnothing}$
or
$head^-(r)={\varnothing}$
or
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
. The set of rules (9)–(10) is denoted as winv(r).
$body^{+}(r)=body^{-}(r)={\varnothing}$
. The set of rules (9)–(10) is denoted as winv(r).
2. Define
where \begin{eqnarray*}wda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; winv(r)\,\}\end{eqnarray*}
\begin{eqnarray*}wda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; winv(r)\,\}\end{eqnarray*}
 $\ell_i$
is either a literal
$\ell_i$
is either a literal
 $L_i$
$L_i$
 $(k+1\le i\le l)$
or an NAF-literal
$(k+1\le i\le l)$
or an NAF-literal
 $not\,L_i$
$not\,L_i$
 $(1\le i\le k)$
, and each
$(1\le i\le k)$
, and each
 $\Gamma_j$
$\Gamma_j$
 $(1\le j\le p)$
is a disjunction of literals and NAF-literals.
$(1\le j\le p)$
is a disjunction of literals and NAF-literals.3. The weak DA completion of
 $\Pi$
is defined as:
$\Pi$
is defined as:  $$ WDA(\Pi)=\Pi \;\cup\; wda(\Pi).$$
$$ WDA(\Pi)=\Pi \;\cup\; wda(\Pi).$$
(9) and (10) in winv(r) represent inverse implication from the (default) negation of the conjunction in the body of r to the (default) negation of the disjunction in the head of r.
![]() $wda(\Pi)$
collects rules “
$wda(\Pi)$
collects rules “
![]() $\ell_i\leftarrow \Gamma_j$
"
$\ell_i\leftarrow \Gamma_j$
"
![]() $(1\leq j\leq p)$
having the same (NAF-)literal
$(1\leq j\leq p)$
having the same (NAF-)literal
![]() $\ell_i$
on the left of “
$\ell_i$
on the left of “
![]() $\leftarrow,$
" and constructs “
$\leftarrow,$
" and constructs “
![]() $\ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p$
," which we call an extended rule. Introducing
$\ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p$
," which we call an extended rule. Introducing
![]() $wda(\Pi)$
to
$wda(\Pi)$
to
![]() $\Pi$
realizes reasoning by weak DA. An extended rule has a conjunction of disjunctions in its body, while it is transformed to rules of a GEDP as the case of AC completion. That is, the extended rule:
$\Pi$
realizes reasoning by weak DA. An extended rule has a conjunction of disjunctions in its body, while it is transformed to rules of a GEDP as the case of AC completion. That is, the extended rule:
is identified with the set of
![]() $(m_1\times\cdots\times m_p)$
rules of the form:
$(m_1\times\cdots\times m_p)$
rules of the form:
By this fact,
![]() $WDA(\Pi)$
is viewed as a GEDP and we do not distinguish extended rules and rules of a GEDP hereafter. The semantics of
$WDA(\Pi)$
is viewed as a GEDP and we do not distinguish extended rules and rules of a GEDP hereafter. The semantics of
![]() $WDA(\Pi)$
is defined by its answer sets.
$WDA(\Pi)$
is defined by its answer sets.
Example 3.9 Let
![]() $\Pi$
be the program:
$\Pi$
be the program:
 \begin{eqnarray*}&& p\,;\,q\leftarrow r,\, not\,s,\\&& q\,;\,not\,r\leftarrow t,\\&& s\leftarrow.\end{eqnarray*}
\begin{eqnarray*}&& p\,;\,q\leftarrow r,\, not\,s,\\&& q\,;\,not\,r\leftarrow t,\\&& s\leftarrow.\end{eqnarray*}
Then,
![]() $wda(\Pi)$
becomes
$wda(\Pi)$
becomes
 \begin{eqnarray*}&& not\,p\leftarrow not\,r\, ;\, s,\\&& not\,q\leftarrow (not\,r\,;\, s),\, not\,t,\\&& r\leftarrow not\,t\end{eqnarray*}
\begin{eqnarray*}&& not\,p\leftarrow not\,r\, ;\, s,\\&& not\,q\leftarrow (not\,r\,;\, s),\, not\,t,\\&& r\leftarrow not\,t\end{eqnarray*}
where the first rule “
![]() $not\,p\leftarrow not\,r\, ;\, s$
" is identified with
$not\,p\leftarrow not\,r\, ;\, s$
" is identified with
and the second rule “
![]() $not\,q\leftarrow (not\,r\,;\, s),\, not\,t$
" is identified with
$not\,q\leftarrow (not\,r\,;\, s),\, not\,t$
" is identified with
Then,
![]() $WDA(\Pi)$
has the answer set
$WDA(\Pi)$
has the answer set
![]() $\{ s, r\}$
.
$\{ s, r\}$
.
As in the case of AC completion, if there is more than one rule having the same (NAF-)literal in the heads, they are collected to produce a single inverse rule. For instance,
![]() $\Pi=\{\,p\leftarrow q,\;\; p\leftarrow~r\,\}$
produces
$\Pi=\{\,p\leftarrow q,\;\; p\leftarrow~r\,\}$
produces
![]() $wda(\Pi)=\{\, not\,p\leftarrow not\,q,\,not\,r\,\}$
but not
$wda(\Pi)=\{\, not\,p\leftarrow not\,q,\,not\,r\,\}$
but not
![]() $\Lambda=\{\, not\,p\leftarrow not\,q,\;\; not\,p\leftarrow not\,r\,\}$
. Suppose that the new fact “
$\Lambda=\{\, not\,p\leftarrow not\,q,\;\; not\,p\leftarrow not\,r\,\}$
. Suppose that the new fact “
![]() $r\leftarrow$
” is added to
$r\leftarrow$
” is added to
![]() $\Pi$
. Put
$\Pi$
. Put
![]() $\Pi'=\Pi\cup\{ r\leftarrow\}$
. Then,
$\Pi'=\Pi\cup\{ r\leftarrow\}$
. Then,
![]() $WDA(\Pi')$
has the answer set
$WDA(\Pi')$
has the answer set
![]() $\{p,r\}$
. If
$\{p,r\}$
. If
![]() $\Lambda$
is used instead of
$\Lambda$
is used instead of
![]() $wda(\Pi)$
, however,
$wda(\Pi)$
, however,
![]() $\Pi'\cup\Lambda$
is incoherent because the first rule of
$\Pi'\cup\Lambda$
is incoherent because the first rule of
![]() $\Lambda$
is not satisfied. The result is too strong because p is deduced by “
$\Lambda$
is not satisfied. The result is too strong because p is deduced by “
![]() $p\leftarrow r$
" and “
$p\leftarrow r$
" and “
![]() $r\leftarrow,$
" and it has no direct connection to DA inference in the first rule of
$r\leftarrow,$
" and it has no direct connection to DA inference in the first rule of
![]() $\Lambda$
. Hence, we conclude
$\Lambda$
. Hence, we conclude
![]() $not\,p$
if both q and r are negated in
$not\,p$
if both q and r are negated in
![]() $wda(\Pi)$
.
$wda(\Pi)$
.
The strong DA completion is defined in a similar manner.
Definition 3.4 (strong DA completion) Let
![]() $\Pi$
be a program and
$\Pi$
be a program and
![]() $r\in\Pi$
a rule of the form:
$r\in\Pi$
a rule of the form:
1. For each disjunct in
 $head^+(r)$
and
$head^+(r)$
and
 $head^-(r)$
, inverse the implication: (11)
$head^-(r)$
, inverse the implication: (11) \begin{eqnarray}\neg\,L_i &\leftarrow& \neg\,L_{l+1}\,;\,\cdots\, ;\, \neg\,L_m\,;\, L_{m+1}\,;\cdots\, ;\, L_n\;\; (1\leq i\leq k), \end{eqnarray}
\begin{eqnarray}\neg\,L_i &\leftarrow& \neg\,L_{l+1}\,;\,\cdots\, ;\, \neg\,L_m\,;\, L_{m+1}\,;\cdots\, ;\, L_n\;\; (1\leq i\leq k), \end{eqnarray}
As in the case of WDA, the produced (11) (resp. (12)) is considered an abbreviation of the collection of
![]() $(n-l)$
rules:
$(n-l)$
rules:
![]() $(\neg\,L_i \leftarrow \neg\,L_{l+1}),\ldots, (\neg\,L_i \leftarrow L_n)$
(resp.
$(\neg\,L_i \leftarrow \neg\,L_{l+1}),\ldots, (\neg\,L_i \leftarrow L_n)$
(resp.
![]() $(L_i \leftarrow \neg\,L_{l+1}),\ldots, (L_i \leftarrow L_n)$
), hence we call (11) or (12) a rule. In particular, (11) is not produced if
$(L_i \leftarrow \neg\,L_{l+1}),\ldots, (L_i \leftarrow L_n)$
), hence we call (11) or (12) a rule. In particular, (11) is not produced if
![]() $head^+(r)={\varnothing}$
or
$head^+(r)={\varnothing}$
or
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
, and (12) is not produced if
$body^{+}(r)=body^{-}(r)={\varnothing}$
, and (12) is not produced if
![]() $head^-(r)={\varnothing}$
or
$head^-(r)={\varnothing}$
or
![]() $body^{+}(r)=body^{-}(r)={\varnothing}$
. The set of rules (11)–(12) is denoted as sinv(r).
$body^{+}(r)=body^{-}(r)={\varnothing}$
. The set of rules (11)–(12) is denoted as sinv(r).
2. Define
where \begin{eqnarray*}sda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; sinv(r)\,\}\end{eqnarray*}
\begin{eqnarray*}sda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; sinv(r)\,\}\end{eqnarray*}
 $\ell_i$
is either a literal
$\ell_i$
is either a literal
 $L_i$
$L_i$
 $(k+1\le i\le l)$
or
$(k+1\le i\le l)$
or
 $\neg\,L_i$
$\neg\,L_i$
 $(1\le i\le k)$
, and each
$(1\le i\le k)$
, and each
 $\Gamma_j$
$\Gamma_j$
 $(1\le j\le p)$
is a disjunction of positive/negative literals.
$(1\le j\le p)$
is a disjunction of positive/negative literals.3. The strong DA completion of
 $\Pi$
is defined as:
$\Pi$
is defined as:  $$ SDA(\Pi)=\Pi \;\cup\; sda(\Pi).$$
$$ SDA(\Pi)=\Pi \;\cup\; sda(\Pi).$$
As in the case of WDA, extended rules in
![]() $sda(\Pi)$
are transformed to rules of a GEDP. Then,
$sda(\Pi)$
are transformed to rules of a GEDP. Then,
![]() $SDA(\Pi)$
is viewed as a GEDP and its semantics is defined by its answer sets. In particular,
$SDA(\Pi)$
is viewed as a GEDP and its semantics is defined by its answer sets. In particular,
![]() $SDA(\Pi)$
becomes an EDP if
$SDA(\Pi)$
becomes an EDP if
![]() $\Pi$
is an EDP.
$\Pi$
is an EDP.
The result of DA completion is syntax-dependent in general.
Example 3.10 Let
![]() $\Pi_1=\{\, not\,p\leftarrow q\,\}$
and
$\Pi_1=\{\, not\,p\leftarrow q\,\}$
and
![]() $\Pi_2=\{\, \leftarrow p,q \,\}$
where
$\Pi_2=\{\, \leftarrow p,q \,\}$
where
![]() $\Pi_1$
and
$\Pi_1$
and
![]() $\Pi_2$
are equivalent (Proposition 2.1). Then,
$\Pi_2$
are equivalent (Proposition 2.1). Then,
![]() $WDA(\Pi_1)=\Pi_1\cup \{\, p\leftarrow not\,q\,\}$
and
$WDA(\Pi_1)=\Pi_1\cup \{\, p\leftarrow not\,q\,\}$
and
![]() $WDA(\Pi_2)=\Pi_2$
. As a result,
$WDA(\Pi_2)=\Pi_2$
. As a result,
![]() $WDA(\Pi_1)$
has the answer set
$WDA(\Pi_1)$
has the answer set
![]() $\{p\}$
while
$\{p\}$
while
![]() $WDA(\Pi_2)$
has the answer set
$WDA(\Pi_2)$
has the answer set
![]() ${\varnothing}$
.
${\varnothing}$
.
Both WDA and SDA are nonmonotonic in general.
Example 3.11 (1)
![]() $\Pi_1=\{\, p\leftarrow not\,q,\;\; not\,q\leftarrow p\,\}$
produces
$\Pi_1=\{\, p\leftarrow not\,q,\;\; not\,q\leftarrow p\,\}$
produces
![]() $WDA(\Pi_1)=\Pi_1\cup \{\, not\,p\leftarrow q,\;\; q\leftarrow not\,p\,\}$
. Then,
$WDA(\Pi_1)=\Pi_1\cup \{\, not\,p\leftarrow q,\;\; q\leftarrow not\,p\,\}$
. Then,
![]() $\Pi_1\models_s p$
but
$\Pi_1\models_s p$
but
![]() $WDA(\Pi_1)\not\models_s p$
. (2)
$WDA(\Pi_1)\not\models_s p$
. (2)
![]() $\Pi_2=\{\, p\leftarrow not\,\neg r,\;\; r\leftarrow not\,q,\;\; q\leftarrow\,\}$
produces
$\Pi_2=\{\, p\leftarrow not\,\neg r,\;\; r\leftarrow not\,q,\;\; q\leftarrow\,\}$
produces
![]() $SDA(\Pi_2)=\Pi_2\cup \{\, \neg\,p\leftarrow \neg\,r,\;\; \neg\,r\leftarrow q\,\}$
. Then,
$SDA(\Pi_2)=\Pi_2\cup \{\, \neg\,p\leftarrow \neg\,r,\;\; \neg\,r\leftarrow q\,\}$
. Then,
![]() $\Pi_2\models_c p$
but
$\Pi_2\models_c p$
but
![]() $SDA(\Pi_2)\not\models_c p$
.
$SDA(\Pi_2)\not\models_c p$
.
When a program is a consistent EDP, the WDA does not introduce a new answer set.
Proposition 3.6 Let
![]() $\Pi$
be an EDP. If S is a consistent answer set of
$\Pi$
be an EDP. If S is a consistent answer set of
![]() $WDA(\Pi)$
, then S is an answer set of
$WDA(\Pi)$
, then S is an answer set of
![]() $\Pi$
.
$\Pi$
.
Proof. When
![]() $\Pi$
is an EDP, the rules (10) are not included in winv(r). By the rules (9) in winv(r), rules of the form (
$\Pi$
is an EDP, the rules (10) are not included in winv(r). By the rules (9) in winv(r), rules of the form (
![]() $not\,L_i\leftarrow \Gamma_1,\ldots, \Gamma_p$
) are produced in
$not\,L_i\leftarrow \Gamma_1,\ldots, \Gamma_p$
) are produced in
![]() $wda(\Pi)$
, which are identified with the collection of rules (
$wda(\Pi)$
, which are identified with the collection of rules (
![]() $not\,L_i\leftarrow \ell_{j_1}^1,\ldots \ell_{j_p}^p$
) where
$not\,L_i\leftarrow \ell_{j_1}^1,\ldots \ell_{j_p}^p$
) where
![]() $\ell_{j_k}^p$
$\ell_{j_k}^p$
![]() $(1\le k\le p)$
is an (NAF-)literal. These rules are converted into the strongly equivalent constraint (
$(1\le k\le p)$
is an (NAF-)literal. These rules are converted into the strongly equivalent constraint (
![]() $\leftarrow L_i,\ell_{j_1}^1,\ldots, \ell_{j_p}^p$
) (Proposition 2.1). The additional constraints may eliminate answer sets of
$\leftarrow L_i,\ell_{j_1}^1,\ldots, \ell_{j_p}^p$
) (Proposition 2.1). The additional constraints may eliminate answer sets of
![]() $\Pi$
, but do not introduce new answer sets. Thus, a consistent answer set S of
$\Pi$
, but do not introduce new answer sets. Thus, a consistent answer set S of
![]() $WDA(\Pi)$
is also a consistent answer set of
$WDA(\Pi)$
is also a consistent answer set of
![]() $\Pi$
.
$\Pi$
.
Proposition 3.7 If a program
![]() $\Pi$
has the answer set Lit, then both
$\Pi$
has the answer set Lit, then both
![]() $WDA(\Pi)$
and
$WDA(\Pi)$
and
![]() $SDA(\Pi)$
have the answer set Lit. In particular, if
$SDA(\Pi)$
have the answer set Lit. In particular, if
![]() $\Pi$
is a contradictory EDP, then
$\Pi$
is a contradictory EDP, then
![]() $SDA(\Pi)$
is contradictory.
$SDA(\Pi)$
is contradictory.
Proof. The proof is similar to Proposition 3.2. In particular, if
![]() $\Pi$
is an EDP, then
$\Pi$
is an EDP, then
![]() $SDA(\Pi)$
is an EDP and the result holds.
$SDA(\Pi)$
is an EDP and the result holds.
As in the case of AC, a consistent program
![]() $\Pi$
may produce an inconsistent
$\Pi$
may produce an inconsistent
![]() $WDA(\Pi)$
or
$WDA(\Pi)$
or
![]() $SDA(\Pi)$
. In converse, an incoherent
$SDA(\Pi)$
. In converse, an incoherent
![]() $\Pi$
may produce a consistent
$\Pi$
may produce a consistent
![]() $WDA(\Pi)$
or
$WDA(\Pi)$
or
![]() $SDA(\Pi)$
.
$SDA(\Pi)$
.
(1)
 $\Pi_1=\{\, not\, p\leftarrow p\,\}$
, which is equivalent to
$\Pi_1=\{\, not\, p\leftarrow p\,\}$
, which is equivalent to
 $\{\,\leftarrow p\,\}$
(Proposition 2.1), is consistent, but
$\{\,\leftarrow p\,\}$
(Proposition 2.1), is consistent, but
 $WDA(\Pi_1)=\Pi_1\cup\{\, p\leftarrow not\,p\,\}$
is incoherent.
$WDA(\Pi_1)=\Pi_1\cup\{\, p\leftarrow not\,p\,\}$
is incoherent.(2)
 $\Pi_2=\{\,\neg\,p\leftarrow p,\;\; \neg\,p\leftarrow\,\}$
is consistent, but
$\Pi_2=\{\,\neg\,p\leftarrow p,\;\; \neg\,p\leftarrow\,\}$
is consistent, but
 $SDA(\Pi_2)\!=\Pi_2\cup\{\, p\leftarrow \neg\,p\,\}$
is contradictory.
$SDA(\Pi_2)\!=\Pi_2\cup\{\, p\leftarrow \neg\,p\,\}$
is contradictory.(3)
 $\Pi_3=\{\, not\,p\leftarrow q,\;\;\leftarrow not\,p\,\}$
, which is equivalent to
$\Pi_3=\{\, not\,p\leftarrow q,\;\;\leftarrow not\,p\,\}$
, which is equivalent to
 $\{\,\leftarrow p,q,\;\; \leftarrow not\,p\,\}$
(Proposition 2.1), is incoherent, but
$\{\,\leftarrow p,q,\;\; \leftarrow not\,p\,\}$
(Proposition 2.1), is incoherent, but
 $WDA(\Pi_3)=\Pi_3\cup\{\, p\leftarrow not\,q\,\}$
is consistent (having the answer set
$WDA(\Pi_3)=\Pi_3\cup\{\, p\leftarrow not\,q\,\}$
is consistent (having the answer set
 $\{p\}$
).
$\{p\}$
).(4)
 $\Pi_4=\{\, \leftarrow not\,p,\;\; \neg\, p\leftarrow not\,q,\;\; q\leftarrow\,\}$
is incoherent, but
$\Pi_4=\{\, \leftarrow not\,p,\;\; \neg\, p\leftarrow not\,q,\;\; q\leftarrow\,\}$
is incoherent, but
 $SDA(\Pi_4)=\Pi_4\cup\{\, p\leftarrow q\,\}$
is consistent (having the answer set
$SDA(\Pi_4)=\Pi_4\cup\{\, p\leftarrow q\,\}$
is consistent (having the answer set
 $\{p,q\}$
).
$\{p,q\}$
).
4 AC and DA as default reasoning
AC and DA are logically invalid and additional rules for AC and DA often make a program inconsistent. In this section, we relax the effects of the AC or DA completion by introducing additional rules as default rules in the sense of Reiter (Reference Reiter1980). More precisely, we capture AC and DA as the following default inference rules:
 \begin{eqnarray*}({\bf default\, AC}) &&\frac{({\varphi}\Rightarrow \psi)\wedge \psi : {\varphi}}{{\varphi}} \\({\bf default\, DA}) && \frac{({\varphi}\Rightarrow \psi)\wedge \neg{\varphi} : \neg\psi}{\neg\psi}\end{eqnarray*}
\begin{eqnarray*}({\bf default\, AC}) &&\frac{({\varphi}\Rightarrow \psi)\wedge \psi : {\varphi}}{{\varphi}} \\({\bf default\, DA}) && \frac{({\varphi}\Rightarrow \psi)\wedge \neg{\varphi} : \neg\psi}{\neg\psi}\end{eqnarray*}
The default AC rule says: given the conditional “
![]() ${\varphi}\Rightarrow \psi$
" and the fact
${\varphi}\Rightarrow \psi$
" and the fact
![]() $\psi$
, conclude
$\psi$
, conclude
![]() ${\varphi}$
as a default consequence. Likewise, the default DA rule says: given the conditional “
${\varphi}$
as a default consequence. Likewise, the default DA rule says: given the conditional “
![]() ${\varphi}\Rightarrow \psi$
" and the fact
${\varphi}\Rightarrow \psi$
" and the fact
![]() $\neg{\varphi}$
, conclude
$\neg{\varphi}$
, conclude
![]() $\neg\psi$
as a default consequence. We encode these rules in ASP.
$\neg\psi$
as a default consequence. We encode these rules in ASP.
4.1 Default AC completion
The AC completion is modified for default AC reasoning.
Definition 4.1 (default AC completion) Let
![]() $\Pi$
be a program. For each rule
$\Pi$
be a program. For each rule
![]() $r\in\Pi$
of the form:
$r\in\Pi$
of the form:
define dac(r) as the set of rules:
where
![]() $\Delta=not\,\neg\,L_{l+1},\,\ldots,\,not\,\neg\, L_m,\, not\,L_{m+1},\,\ldots,\,not\,L_n$
. As before, (13) is not produced if
$\Delta=not\,\neg\,L_{l+1},\,\ldots,\,not\,\neg\, L_m,\, not\,L_{m+1},\,\ldots,\,not\,L_n$
. As before, (13) is not produced if
![]() $head^+(r)={\varnothing}$
or
$head^+(r)={\varnothing}$
or
![]() $body^+(r)=body^-(r)={\varnothing}$
; and (14) is not produced if
$body^+(r)=body^-(r)={\varnothing}$
; and (14) is not produced if
![]() $head^-(r)={\varnothing}$
or
$head^-(r)={\varnothing}$
or
![]() $body^+(r)=body^-(r)={\varnothing}$
. The default AC completion of
$body^+(r)=body^-(r)={\varnothing}$
. The default AC completion of
![]() $\Pi$
is defined as:
$\Pi$
is defined as:
in which
 \begin{eqnarray*}dac(\Pi)&\!=\!& \{\; \Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; \ell_j,\,\Delta_i \;\mid\\&& \quad \Sigma_i\leftarrow \ell_j,\,\Delta_i \;\, (1\le i\le p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\, dac(r)\, \}\end{eqnarray*}
\begin{eqnarray*}dac(\Pi)&\!=\!& \{\; \Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; \ell_j,\,\Delta_i \;\mid\\&& \quad \Sigma_i\leftarrow \ell_j,\,\Delta_i \;\, (1\le i\le p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\, dac(r)\, \}\end{eqnarray*}
where each
![]() $\Sigma_i$
$\Sigma_i$
![]() $(1\le i\le p)$
is a conjunction of literals and NAF-literals, and
$(1\le i\le p)$
is a conjunction of literals and NAF-literals, and
![]() $\ell_j$
is either a literal
$\ell_j$
is either a literal
![]() $L_j$
$L_j$
![]() $(1\le j\le k)$
or an NAF-literal
$(1\le j\le k)$
or an NAF-literal
![]() $not\,L_j$
$not\,L_j$
![]() $(k+1\le j\le l)$
.
$(k+1\le j\le l)$
.
Like
![]() $AC(\Pi)$
, rules in
$AC(\Pi)$
, rules in
![]() $dac(\Pi)$
are converted into the form of a GEDP, then
$dac(\Pi)$
are converted into the form of a GEDP, then
![]() $DAC(\Pi)$
is viewed as a GEDP. Compared with the AC completion, the DAC completion introduces the conjunction
$DAC(\Pi)$
is viewed as a GEDP. Compared with the AC completion, the DAC completion introduces the conjunction
![]() $\Delta$
of NAF-literals to the body of each rule. Then, the rules “
$\Delta$
of NAF-literals to the body of each rule. Then, the rules “
![]() $\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \,\leftarrow \, \ell_j,\,\Delta_i$
" having the same head with different bodies are constructed for
$\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \,\leftarrow \, \ell_j,\,\Delta_i$
" having the same head with different bodies are constructed for
![]() $i=1,\ldots,p$
.
$i=1,\ldots,p$
.
Example 4.1 Let
![]() $\Pi=\{\,p\leftarrow q,\;\; p\leftarrow r,\;\; p\leftarrow,\;\; \neg r\leftarrow\,\}$
. Then,
$\Pi=\{\,p\leftarrow q,\;\; p\leftarrow r,\;\; p\leftarrow,\;\; \neg r\leftarrow\,\}$
. Then,
![]() $DAC(\Pi)=\Pi\cup dac(\Pi)$
where
$DAC(\Pi)=\Pi\cup dac(\Pi)$
where
As a result,
![]() $DAC(\Pi)$
has the answer set
$DAC(\Pi)$
has the answer set
![]() $\{p,q,\neg r\}$
.
$\{p,q,\neg r\}$
.
We say that a set S of ground literals satisfies the conjunction “
![]() $L_1,\ldots,L_k$
" of ground literals if
$L_1,\ldots,L_k$
" of ground literals if
![]() $\{L_1,\ldots,L_k\}\subseteq S$
; and S satisfies the conjunction “
$\{L_1,\ldots,L_k\}\subseteq S$
; and S satisfies the conjunction “
![]() $not\,L_1,\ldots,not\,L_k$
" of ground NAF-literals if
$not\,L_1,\ldots,not\,L_k$
" of ground NAF-literals if
![]() $\{L_1,\ldots,L_k\}\cap S={\varnothing}$
.
$\{L_1,\ldots,L_k\}\cap S={\varnothing}$
.
When
![]() $AC(\Pi)$
has a consistent answer set,
$AC(\Pi)$
has a consistent answer set,
![]() $DAC(\Pi)$
does not change it.
$DAC(\Pi)$
does not change it.
Proposition 4.1 Let
![]() $\Pi$
be a program. If
$\Pi$
be a program. If
![]() $AC(\Pi)$
has a consistent answer set S, then S is an answer set of
$AC(\Pi)$
has a consistent answer set S, then S is an answer set of
![]() $DAC(\Pi)$
.
$DAC(\Pi)$
.
Proof. Suppose that
![]() $AC(\Pi)$
has a consistent answer set S. For each rule (
$AC(\Pi)$
has a consistent answer set S. For each rule (
![]() $\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; L_j$
)
$\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; L_j$
)
![]() $(1\le j\le k)$
in
$(1\le j\le k)$
in
![]() $ac(\Pi)$
,
$ac(\Pi)$
,
![]() $L_j\in S$
implies that S satisfies some conjunction
$L_j\in S$
implies that S satisfies some conjunction
![]() $\Sigma_i$
$\Sigma_i$
![]() $(1\le i\le p)$
. In this case, S satisfies
$(1\le i\le p)$
. In this case, S satisfies
![]() $\Delta_i$
and
$\Delta_i$
and
![]() $L_j\in S$
implies that S satisfies
$L_j\in S$
implies that S satisfies
![]() $\Sigma_i$
for each rule (
$\Sigma_i$
for each rule (
![]() $\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; L_j,\Delta_i$
) in
$\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; L_j,\Delta_i$
) in
![]() $dac(\Pi)$
. Likewise, for each rule (
$dac(\Pi)$
. Likewise, for each rule (
![]() $\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; not\,L_j$
)
$\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; not\,L_j$
)
![]() $(k+1\le j\le l)$
in
$(k+1\le j\le l)$
in
![]() $ac(\Pi)$
,
$ac(\Pi)$
,
![]() $L_j\not\in S$
implies that S satisfies some
$L_j\not\in S$
implies that S satisfies some
![]() $\Sigma_i$
$\Sigma_i$
![]() $(1\le i\le p)$
. In this case, S satisfies
$(1\le i\le p)$
. In this case, S satisfies
![]() $\Delta_i$
and
$\Delta_i$
and
![]() $L_j\not\in S$
implies that S satisfies
$L_j\not\in S$
implies that S satisfies
![]() $\Sigma_i$
for each rule (
$\Sigma_i$
for each rule (
![]() $\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; not\,L_j,\Delta_i$
) in
$\Sigma_1\,;\,\cdots\, ;\,\Sigma_p \;\leftarrow \; not\,L_j,\Delta_i$
) in
![]() $dac(\Pi)$
. Then,
$dac(\Pi)$
. Then,
![]() $AC(\Pi)^S=DAC(\Pi)^S$
and the result follows.
$AC(\Pi)^S=DAC(\Pi)^S$
and the result follows.
DAC does not introduce the contradictory answer set Lit unless the original program has Lit as an answer set.
Proposition 4.2 Let
![]() $\Pi$
be a program. If
$\Pi$
be a program. If
![]() $DAC(\Pi)$
has the answer set Lit, then
$DAC(\Pi)$
has the answer set Lit, then
![]() $\Pi$
has the answer set Lit.
$\Pi$
has the answer set Lit.
Proof. If
![]() $DAC(\Pi)$
has the answer set Lit, then
$DAC(\Pi)$
has the answer set Lit, then
![]() $DAC(\Pi)^{Lit}=\Pi^{Lit}\cup dac(\Pi)^{Lit}$
has the answer set Lit. Since
$DAC(\Pi)^{Lit}=\Pi^{Lit}\cup dac(\Pi)^{Lit}$
has the answer set Lit. Since
![]() $dac(\Pi)^{Lit}={\varnothing}$
,
$dac(\Pi)^{Lit}={\varnothing}$
,
![]() $\Pi^{Lit}$
has the answer set Lit. Hence,
$\Pi^{Lit}$
has the answer set Lit. Hence,
![]() $\Pi$
has the answer set Lit.
$\Pi$
has the answer set Lit.
![]() $DAC(\Pi)$
possibly turns a contradictory
$DAC(\Pi)$
possibly turns a contradictory
![]() $AC(\Pi)$
into a consistent program.
$AC(\Pi)$
into a consistent program.
Example 4.2 (cont. Example 3.4) Let
![]() $\Pi_1=\{\, p\leftarrow \neg\, p,\;\; p\leftarrow \,\}$
. Then,
$\Pi_1=\{\, p\leftarrow \neg\, p,\;\; p\leftarrow \,\}$
. Then,
![]() $DAC(\Pi_1)=\Pi_1\cup \{\, \neg\, p\leftarrow p,\, not\,p \,\}$
has the single answer set
$DAC(\Pi_1)=\Pi_1\cup \{\, \neg\, p\leftarrow p,\, not\,p \,\}$
has the single answer set
![]() $\{\,p\,\}$
. So
$\{\,p\,\}$
. So
![]() $AC(\Pi_1)$
is contradictory, but
$AC(\Pi_1)$
is contradictory, but
![]() $DAC(\Pi_1)$
is consistent.
$DAC(\Pi_1)$
is consistent.
When
![]() $AC(\Pi)$
is incoherent,
$AC(\Pi)$
is incoherent,
![]() $DAC(\Pi)$
does not resolve incoherency in general.
$DAC(\Pi)$
does not resolve incoherency in general.
Example 4.3 Let
![]() $\Pi=\{\, p\leftarrow q,\;\; p\leftarrow,\;\; \leftarrow q \,\}$
. Then,
$\Pi=\{\, p\leftarrow q,\;\; p\leftarrow,\;\; \leftarrow q \,\}$
. Then,
![]() $AC(\Pi)=\Pi\cup \{\, q\leftarrow p \,\}$
is incoherent.
$AC(\Pi)=\Pi\cup \{\, q\leftarrow p \,\}$
is incoherent.
![]() $DAC(\Pi)=\Pi\cup \{\, q\leftarrow p,\, not\,\neg\,q \,\}$
is still incoherent.
$DAC(\Pi)=\Pi\cup \{\, q\leftarrow p,\, not\,\neg\,q \,\}$
is still incoherent.
4.2 Default DA completion
The DA completion is modified for default DA reasoning.
Definition 4.2 (default DA completion) Let
![]() $\Pi$
be a program. Define
$\Pi$
be a program. Define
 \begin{eqnarray*}wdda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p,\,\delta^w_i \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; winv(r)\,\},\\sdda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p,\,\delta^s_i \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; sinv(r)\,\}\end{eqnarray*}
\begin{eqnarray*}wdda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p,\,\delta^w_i \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; winv(r)\,\},\\sdda(\Pi) &\!=\!& \{\, \ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p,\,\delta^s_i \,\mid \\&& \quad \ell_i\leftarrow \Gamma_j\; (1\leq j\leq p)\;\;\mbox{is in}\;\; \bigcup_{r\in\Pi}\; sinv(r)\,\}\end{eqnarray*}
where
![]() $\ell_i$
,
$\ell_i$
,
![]() $\Gamma_j$
, winv(r), and sinv(r) are the same as those in Definitions 3.3 and 3.4. In addition,
$\Gamma_j$
, winv(r), and sinv(r) are the same as those in Definitions 3.3 and 3.4. In addition,
![]() $\delta^w_i=not\,\neg\,L_i$
if
$\delta^w_i=not\,\neg\,L_i$
if
![]() $\ell_i=L_i$
, and
$\ell_i=L_i$
, and
![]() $\delta^w_i=not\,L_i$
if
$\delta^w_i=not\,L_i$
if
![]() $\ell_i=not\,L_i$
;
$\ell_i=not\,L_i$
;
![]() $\delta^s_i=not\,\neg\,L_i$
if
$\delta^s_i=not\,\neg\,L_i$
if
![]() $\ell_i=L_i$
, and
$\ell_i=L_i$
, and
![]() $\delta^s_i=not\,L_i$
if
$\delta^s_i=not\,L_i$
if
![]() $\ell_i=\neg\,L_i$
. The weak default DA completion and the strong default DA completion of
$\ell_i=\neg\,L_i$
. The weak default DA completion and the strong default DA completion of
![]() $\Pi$
are respectively defined as:
$\Pi$
are respectively defined as:
Rules in
![]() $wdda(\Pi)$
and
$wdda(\Pi)$
and
![]() $sdda(\Pi)$
are converted into the form of a GEDP, so
$sdda(\Pi)$
are converted into the form of a GEDP, so
![]() $WDDA(\Pi)$
and
$WDDA(\Pi)$
and
![]() $SDDA(\Pi)$
are viewed as GEDPs. Like the DAC completion, both WDDA and SDDA introduce an additional NAF-literal to each rule.
$SDDA(\Pi)$
are viewed as GEDPs. Like the DAC completion, both WDDA and SDDA introduce an additional NAF-literal to each rule.
When
![]() $WDA(\Pi)$
(resp.
$WDA(\Pi)$
(resp.
![]() $SDA(\Pi)$
) has a consistent answer set,
$SDA(\Pi)$
) has a consistent answer set,
![]() $WDDA(\Pi)$
(resp.
$WDDA(\Pi)$
(resp.
![]() $SDDA(\Pi)$
) does not change it.
$SDDA(\Pi)$
) does not change it.
Proposition 4.3 Let
![]() $\Pi$
be a program. If
$\Pi$
be a program. If
![]() $WDA(\Pi)$
(resp.
$WDA(\Pi)$
(resp.
![]() $SDA(\Pi)$
) has a consistent answer set S, then S is an answer set of
$SDA(\Pi)$
) has a consistent answer set S, then S is an answer set of
![]() $WDDA(\Pi)$
(resp.
$WDDA(\Pi)$
(resp.
![]() $SDDA(\Pi)$
).
$SDDA(\Pi)$
).
Proof. Suppose that
![]() $WDA(\Pi)$
has a consistent answer set S. If
$WDA(\Pi)$
has a consistent answer set S. If
![]() $L_i\in S,$
then
$L_i\in S,$
then
![]() $\neg\,L_i\not\in S$
and
$\neg\,L_i\not\in S$
and
![]() $\delta^w_i=not\,\neg\,L_i$
is eliminated in
$\delta^w_i=not\,\neg\,L_i$
is eliminated in
![]() $WDDA(\Pi)^S$
. Else if
$WDDA(\Pi)^S$
. Else if
![]() $L_i\not\in S$
and
$L_i\not\in S$
and
![]() $\neg\,L_i\in S$
, there is another rule (
$\neg\,L_i\in S$
, there is another rule (
![]() $\ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p,\,\delta^w_i$
) in
$\ell_i \leftarrow \Gamma_1,\ldots, \Gamma_p,\,\delta^w_i$
) in
![]() $wdda(\Pi)$
such that
$wdda(\Pi)$
such that
![]() $\ell_i=\neg\,L_i$
and
$\ell_i=\neg\,L_i$
and
![]() $\delta^w_i=not\,L_i$
. Then,
$\delta^w_i=not\,L_i$
. Then,
![]() $\delta^w_i=not\,L_i$
is eliminated in
$\delta^w_i=not\,L_i$
is eliminated in
![]() $WDDA(\Pi)^S$
. Thus,
$WDDA(\Pi)^S$
. Thus,
![]() $WDA(\Pi)^S=WDDA(\Pi)^S$
. Similarly,
$WDA(\Pi)^S=WDDA(\Pi)^S$
. Similarly,
![]() $SDA(\Pi)^S=SDDA(\Pi)^S$
. Hence, the result follows.
$SDA(\Pi)^S=SDDA(\Pi)^S$
. Hence, the result follows.
WDDA or SDDA does not introduce the contradictory answer set Lit unless the original program has Lit as an answer set.
Proposition 4.4 Let
![]() $\Pi$
be a program. If
$\Pi$
be a program. If
![]() $WDDA(\Pi)$
(or
$WDDA(\Pi)$
(or
![]() $SDDA(\Pi)$
) has the answer set Lit, then
$SDDA(\Pi)$
) has the answer set Lit, then
![]() $\Pi$
has the answer set Lit.
$\Pi$
has the answer set Lit.
Proof. If
![]() $WDDA(\Pi)$
has the answer Lit, then
$WDDA(\Pi)$
has the answer Lit, then
![]() $WDDA(\Pi)^{Lit}=\Pi^{Lit}\cup wdda(\Pi)^{Lit}$
has the answer set Lit. Since
$WDDA(\Pi)^{Lit}=\Pi^{Lit}\cup wdda(\Pi)^{Lit}$
has the answer set Lit. Since
![]() $wdda(\Pi)^{Lit}={\varnothing}$
,
$wdda(\Pi)^{Lit}={\varnothing}$
,
![]() $\Pi^{Lit}$
has the answer set Lit. Hence,
$\Pi^{Lit}$
has the answer set Lit. Hence,
![]() $\Pi$
has the answer set Lit. The case of
$\Pi$
has the answer set Lit. The case of
![]() $SDDA(\Pi)$
is proved in a similar manner.
$SDDA(\Pi)$
is proved in a similar manner.
![]() $WDDA(\Pi)$
(resp.
$WDDA(\Pi)$
(resp.
![]() $SDDA(\Pi)$
) possibly turns a contradictory
$SDDA(\Pi)$
) possibly turns a contradictory
![]() $WDA(\Pi)$
(resp.
$WDA(\Pi)$
(resp.
![]() $SDA(\Pi)$
) into a consistent program, while it does not resolve incoherency in general.
$SDA(\Pi)$
) into a consistent program, while it does not resolve incoherency in general.
Example 4.4 (cont. Example 3.12) Let
![]() $\Pi_1=\{\, not\,p\leftarrow p \,\}$
where
$\Pi_1=\{\, not\,p\leftarrow p \,\}$
where
![]() $WDA(\Pi_1)$
is incoherent.
$WDA(\Pi_1)$
is incoherent.
![]() $WDDA(\Pi_1)=\Pi_1\cup \{\, p\leftarrow not\,p,\, not\,\neg\,p \,\}$
is still incoherent. Let
$WDDA(\Pi_1)=\Pi_1\cup \{\, p\leftarrow not\,p,\, not\,\neg\,p \,\}$
is still incoherent. Let
![]() $\Pi_2=\{\, \neg\, p\leftarrow p,\;\;\; \neg\, p\leftarrow \,\}$
where
$\Pi_2=\{\, \neg\, p\leftarrow p,\;\;\; \neg\, p\leftarrow \,\}$
where
![]() $SDA(\Pi_2)$
is contradictory.
$SDA(\Pi_2)$
is contradictory.
![]() $SDDA(\Pi_2)=\Pi_2\cup \{\, p\leftarrow \neg\,p,\, not\,\neg \,p \,\}$
has the consistent answer set
$SDDA(\Pi_2)=\Pi_2\cup \{\, p\leftarrow \neg\,p,\, not\,\neg \,p \,\}$
has the consistent answer set
![]() $\{\neg p\}$
.
$\{\neg p\}$
.
5 Characterizing human reasoning tasks
5.1 Suppression task
Byrne (Reference Byrne1989) provides an empirical study which shows that human conditional reasoning can be nonmonotonic in the so-called suppression tasks. She verifies the effects in different types of conditional reasoning by experimental testing on college students. Students are divided into three groups: the first group receives simple conditional arguments; the second group receives conditional arguments accompanied by another conditional sentence with an alternative antecedent; and the third group receives conditional arguments accompanied by another conditional sentence with an additional antecedent. More precisely, suppose the following three conditional sentences:
![]() $S_1$
: If she has an essay to write then she will study late in the library.
$S_1$
: If she has an essay to write then she will study late in the library.
![]() $S_2$
: If she has some textbooks to read then she will study late in the library.
$S_2$
: If she has some textbooks to read then she will study late in the library.
![]() $S_3$
: If the library stays open then she will study late in the library.
$S_3$
: If the library stays open then she will study late in the library.
Given the conditional sentence
![]() $S_1$
,
$S_1$
,
![]() $S_2$
represents a sentence with an alternative antecedent, while
$S_2$
represents a sentence with an alternative antecedent, while
![]() $S_3$
represents a sentence with an additional antecedent. The antecedent of
$S_3$
represents a sentence with an additional antecedent. The antecedent of
![]() $S_2$
is considered an alternative sufficient condition for studying late in the library. By contrast, the antecedent of
$S_2$
is considered an alternative sufficient condition for studying late in the library. By contrast, the antecedent of
![]() $S_3$
is considered an additional sufficient condition for studying late in the library. Table 1 presents the percentages of inferences made by subjects from the three kinds of arguments.
$S_3$
is considered an additional sufficient condition for studying late in the library. Table 1 presents the percentages of inferences made by subjects from the three kinds of arguments.
Table 1. The percentages of inferences in experiments (Byrne Reference Byrne1989)

By the table, given the sentence
![]() $S_1$
and the fact: “she will study late in the library," the 71% of the first group concludes: “she has an essay to write" by AC. When
$S_1$
and the fact: “she will study late in the library," the 71% of the first group concludes: “she has an essay to write" by AC. When
![]() $S_1$
is accompanied by a conditional
$S_1$
is accompanied by a conditional
![]() $S_2$
containing an alternative antecedent, on the other hand, the percentage of subjects who perform AC inference reduces to 13%. The reason is that people know that the alternative: “She has some textbooks to read,” could be the case instead. Similar reduction is observed for DA. Byrne argues that those fallacious inferences are suppressed when a conditional is accompanied by an alternative antecedent. She also observes that the inference patterns change when
$S_2$
containing an alternative antecedent, on the other hand, the percentage of subjects who perform AC inference reduces to 13%. The reason is that people know that the alternative: “She has some textbooks to read,” could be the case instead. Similar reduction is observed for DA. Byrne argues that those fallacious inferences are suppressed when a conditional is accompanied by an alternative antecedent. She also observes that the inference patterns change when
![]() $S_1$
is accompanied by a conditional
$S_1$
is accompanied by a conditional
![]() $S_3$
containing an additional antecedent. In Table 1, the number of subjects who conclude: “She will study late in the library" by AA reduces to 38%, and the number of subjects who conclude: “She does not have an essay to write" by DC reduces to 33%. By contrast, the suppression of AC and DA are relaxed, 54% of subjects make AC and 63% of subjects make DA. Byrne then argues that “valid inferences are suppressed in the same way as fallacious inferences."
$S_3$
containing an additional antecedent. In Table 1, the number of subjects who conclude: “She will study late in the library" by AA reduces to 38%, and the number of subjects who conclude: “She does not have an essay to write" by DC reduces to 33%. By contrast, the suppression of AC and DA are relaxed, 54% of subjects make AC and 63% of subjects make DA. Byrne then argues that “valid inferences are suppressed in the same way as fallacious inferences."
The suppression task is characterized in our framework as follows. First, the sentence
![]() $S_1$
is represented as the rule: “
$S_1$
is represented as the rule: “
![]() $library \leftarrow essay$
." Then, four conditional inferences (AA, DC, AC, DA) in simple arguments are respectively represented by the following programs:
$library \leftarrow essay$
." Then, four conditional inferences (AA, DC, AC, DA) in simple arguments are respectively represented by the following programs:
 \begin{eqnarray*}\mbox{(AA)} && \Pi_0=\{\, library \leftarrow essay,\;\;\; essay\leftarrow\,\}, \\\mbox{(DC)} && \Pi_1=\{\, library \leftarrow essay,\;\;\; \neg\, library\leftarrow\,\}, \\\mbox{(AC)} && \Pi_2=\{\, library \leftarrow essay,\;\;\; library\leftarrow\,\}, \\\mbox{(DA)} && \Pi_3=\{\, library \leftarrow essay,\;\;\; \neg\,essay\leftarrow\,\}.\end{eqnarray*}
\begin{eqnarray*}\mbox{(AA)} && \Pi_0=\{\, library \leftarrow essay,\;\;\; essay\leftarrow\,\}, \\\mbox{(DC)} && \Pi_1=\{\, library \leftarrow essay,\;\;\; \neg\, library\leftarrow\,\}, \\\mbox{(AC)} && \Pi_2=\{\, library \leftarrow essay,\;\;\; library\leftarrow\,\}, \\\mbox{(DA)} && \Pi_3=\{\, library \leftarrow essay,\;\;\; \neg\,essay\leftarrow\,\}.\end{eqnarray*}
Then,
![]() $\Pi_0$
has the answer set
$\Pi_0$
has the answer set
![]() $\{\,library, essay\,\}$
in which AA inference is done. By contrast, DC, AC, and DA inferences are not performed in
$\{\,library, essay\,\}$
in which AA inference is done. By contrast, DC, AC, and DA inferences are not performed in
![]() $\Pi_1$
,
$\Pi_1$
,
![]() $\Pi_2$
, and
$\Pi_2$
, and
![]() $\Pi_3$
, respectively. To realize those inferences, consider completions such that
$\Pi_3$
, respectively. To realize those inferences, consider completions such that
 \begin{eqnarray*}SDC(\Pi_1)&=&\Pi_1\cup \{\, \neg\,essay \leftarrow \neg\,library\,\}, \\AC(\Pi_2)&=&\Pi_2\cup\{\, essay\leftarrow library \,\}, \\SDA(\Pi_3)&=&\Pi_3\cup\{\, \neg\,library \leftarrow \neg\,essay\,\}\end{eqnarray*}
\begin{eqnarray*}SDC(\Pi_1)&=&\Pi_1\cup \{\, \neg\,essay \leftarrow \neg\,library\,\}, \\AC(\Pi_2)&=&\Pi_2\cup\{\, essay\leftarrow library \,\}, \\SDA(\Pi_3)&=&\Pi_3\cup\{\, \neg\,library \leftarrow \neg\,essay\,\}\end{eqnarray*}
where
![]() $SDC(\Pi_1)$
has the answer set
$SDC(\Pi_1)$
has the answer set
![]() $\{\,\neg\,library, \neg\,essay\,\}$
,
$\{\,\neg\,library, \neg\,essay\,\}$
,
![]() $AC(\Pi_2)$
has the answer set
$AC(\Pi_2)$
has the answer set
![]() $\{\,library, essay\,\}$
, and
$\{\,library, essay\,\}$
, and
![]() $SDA(\Pi_3)$
has the answer set
$SDA(\Pi_3)$
has the answer set
![]() $\{\,\neg\,library, \neg\,essay\,\}$
. As a result, DC, AC, and DA inferences are performed in
$\{\,\neg\,library, \neg\,essay\,\}$
. As a result, DC, AC, and DA inferences are performed in
![]() $SDC(\Pi_1)$
,
$SDC(\Pi_1)$
,
![]() $AC(\Pi_2)$
, and
$AC(\Pi_2)$
, and
![]() $SDA(\Pi_3)$
, respectively.
$SDA(\Pi_3)$
, respectively.
Next, consider the alternative arguments
![]() $S_1$
and
$S_1$
and
![]() $S_2$
. They are represented by the programs:
$S_2$
. They are represented by the programs:
The program
![]() $\Pi_0^{\rm ALT}$
has the answer set
$\Pi_0^{\rm ALT}$
has the answer set
![]() $\{\,library, essay\,\}$
in which the result of AA inference does not change from
$\{\,library, essay\,\}$
in which the result of AA inference does not change from
![]() $\Pi_0$
. Programs
$\Pi_0$
. Programs
![]() $\Pi_1^{\rm ALT}$
,
$\Pi_1^{\rm ALT}$
,
![]() $\Pi_2^{\rm ALT}$
, and
$\Pi_2^{\rm ALT}$
, and
![]() $\Pi_3^{\rm ALT}$
are completed as follows:
$\Pi_3^{\rm ALT}$
are completed as follows:
 \begin{eqnarray*}SDC(\Pi_1^{\rm ALT})&=&\Pi_1^{\rm ALT}\cup \{\, \neg\,essay \leftarrow \neg\,library,\;\;\; \neg\,text \leftarrow \neg\,library\,\}, \\AC(\Pi_2^{\rm ALT})&=&\Pi_2^{\rm ALT}\cup\{\, essay\,;\, text\leftarrow library \,\}, \\SDA(\Pi_3^{\rm ALT})&=&\Pi_3^{\rm ALT}\cup\{\, \neg\,library \leftarrow \neg\,essay,\,\neg\,text\,\}\end{eqnarray*}
\begin{eqnarray*}SDC(\Pi_1^{\rm ALT})&=&\Pi_1^{\rm ALT}\cup \{\, \neg\,essay \leftarrow \neg\,library,\;\;\; \neg\,text \leftarrow \neg\,library\,\}, \\AC(\Pi_2^{\rm ALT})&=&\Pi_2^{\rm ALT}\cup\{\, essay\,;\, text\leftarrow library \,\}, \\SDA(\Pi_3^{\rm ALT})&=&\Pi_3^{\rm ALT}\cup\{\, \neg\,library \leftarrow \neg\,essay,\,\neg\,text\,\}\end{eqnarray*}
where
![]() $SDC(\Pi_1^{\rm ALT})$
has the answer set
$SDC(\Pi_1^{\rm ALT})$
has the answer set
![]() $\{\,\neg\,library, \neg\,essay, \neg\,text\,\}$
,
$\{\,\neg\,library, \neg\,essay, \neg\,text\,\}$
,
![]() $AC(\Pi_2^{\rm ALT})$
has the two answer sets
$AC(\Pi_2^{\rm ALT})$
has the two answer sets
![]() $\{\,library, essay\,\}$
and
$\{\,library, essay\,\}$
and
![]() $\{\,library, text\,\}$
, and
$\{\,library, text\,\}$
, and
![]() $SDA(\Pi_3^{\rm ALT})$
has the answer set
$SDA(\Pi_3^{\rm ALT})$
has the answer set
![]() $\{\,\neg\,essay\,\}$
. As a result,
$\{\,\neg\,essay\,\}$
. As a result,
![]() $SDC(\Pi_1^{\rm ALT})\models_s \neg\,essay$
,
$SDC(\Pi_1^{\rm ALT})\models_s \neg\,essay$
,
![]() $AC(\Pi_2^{\rm ALT})\not\models_s essay$
, and
$AC(\Pi_2^{\rm ALT})\not\models_s essay$
, and
![]() $SDA(\Pi_3^{\rm ALT})\not\models_s \neg\,library$
, which indicate that AC and DA inferences are suppressed while DC is not suppressed. In this way, the completion successfully represents the effect of suppression of AC/DA inference in alternative arguments.
$SDA(\Pi_3^{\rm ALT})\not\models_s \neg\,library$
, which indicate that AC and DA inferences are suppressed while DC is not suppressed. In this way, the completion successfully represents the effect of suppression of AC/DA inference in alternative arguments.
![]() $\circ$
means that inference succeeds;
$\circ$
means that inference succeeds;
![]() $\times$
means that inference is suppressed.
$\times$
means that inference is suppressed.
In additional arguments, on the other hand, Byrne (Reference Byrne1989)observes that AA/DC inference is also suppressed. Our completion method does not characterize the suppression of AA inference because we enable fallacious inferences by AC/DA completion while still keep the valid AA inference. Byrne (Reference Byrne1989) says “ people may consider that certain other conditions are necessary for this conclusion to hold, for example, the library must remain open. Thus, conditionals are frequently elliptical in that information that can be taken for granted is omitted from them." In the above example, the availability of the library is necessary for studying in it but it is just omitted in the initial premises. Then, it is considered that the rule: “
![]() $library\leftarrow essay$
" in mind is overwritten by the rule: “
$library\leftarrow essay$
" in mind is overwritten by the rule: “
![]() $library\leftarrow essay,\, open$
" when the additional antecedent is given. Let
$library\leftarrow essay,\, open$
" when the additional antecedent is given. Let
 \begin{eqnarray*}&& \Pi_0^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; essay\leftarrow\,\}, \\&& \Pi_1^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; \neg\, library\leftarrow\,\}, \\&& \Pi_2^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; library\leftarrow\,\}, \\&& \Pi_3^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; \neg\,essay\leftarrow\,\}.\end{eqnarray*}
\begin{eqnarray*}&& \Pi_0^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; essay\leftarrow\,\}, \\&& \Pi_1^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; \neg\, library\leftarrow\,\}, \\&& \Pi_2^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; library\leftarrow\,\}, \\&& \Pi_3^{\rm ADD}=\{\, library\leftarrow essay,\,open,\;\;\; \neg\,essay\leftarrow\,\}.\end{eqnarray*}
The program
![]() $\Pi_0^{\rm ADD}$
has the answer set
$\Pi_0^{\rm ADD}$
has the answer set
![]() $\{\,essay\,\}$
, thereby
$\{\,essay\,\}$
, thereby
![]() $\Pi_0^{\rm ADD}\not\models_s library$
. Then, the result of AA inference is suppressed. Programs
$\Pi_0^{\rm ADD}\not\models_s library$
. Then, the result of AA inference is suppressed. Programs
![]() $\Pi_1^{\rm ADD}$
,
$\Pi_1^{\rm ADD}$
,
![]() $\Pi_2^{\rm ADD}$
,
$\Pi_2^{\rm ADD}$
,
![]() $\Pi_3^{\rm ADD}$
are completed as follows:
$\Pi_3^{\rm ADD}$
are completed as follows:
 \begin{eqnarray*}SDC(\Pi_1^{\rm ADD})&=&\Pi_1^{\rm ADD}\cup \{\, \neg\,essay\,;\, \neg\,open \leftarrow \neg\,library\,\}, \\AC(\Pi_2^{\rm ADD})&=&\Pi_2^{\rm ADD}\cup\{\, essay\leftarrow library,\;\;\; open\leftarrow library \,\}, \\SDA(\Pi_3^{\rm ADD})&=&\Pi_3^{\rm ADD}\cup\;\{\, \neg\,library \leftarrow \neg\,essay,\;\;\; \neg\,library \leftarrow \neg\,open\,\}\end{eqnarray*}
\begin{eqnarray*}SDC(\Pi_1^{\rm ADD})&=&\Pi_1^{\rm ADD}\cup \{\, \neg\,essay\,;\, \neg\,open \leftarrow \neg\,library\,\}, \\AC(\Pi_2^{\rm ADD})&=&\Pi_2^{\rm ADD}\cup\{\, essay\leftarrow library,\;\;\; open\leftarrow library \,\}, \\SDA(\Pi_3^{\rm ADD})&=&\Pi_3^{\rm ADD}\cup\;\{\, \neg\,library \leftarrow \neg\,essay,\;\;\; \neg\,library \leftarrow \neg\,open\,\}\end{eqnarray*}
where
![]() $SDC(\Pi_1^{\rm ADD})$
has the two answer sets
$SDC(\Pi_1^{\rm ADD})$
has the two answer sets
![]() $\{\,\neg\,library, \neg\,essay\,\}$
and
$\{\,\neg\,library, \neg\,essay\,\}$
and
![]() $\{\,\neg\,library, \neg\,open\,\}$
,
$\{\,\neg\,library, \neg\,open\,\}$
,
![]() $AC(\Pi_2^{\rm ADD})$
has the answer set
$AC(\Pi_2^{\rm ADD})$
has the answer set
![]() $\{\,library, essay, open\,\}$
, and
$\{\,library, essay, open\,\}$
, and
![]() $SDA(\Pi_3^{\rm ADD})$
has the the answer set
$SDA(\Pi_3^{\rm ADD})$
has the the answer set
![]() $\{\,\neg\,essay, \neg\,library\,\}$
. As a result,
$\{\,\neg\,essay, \neg\,library\,\}$
. As a result,
![]() $SDC(\Pi_1^{\rm ADD})\not\models_s \neg\,essay$
,
$SDC(\Pi_1^{\rm ADD})\not\models_s \neg\,essay$
,
![]() $AC(\Pi_2^{\rm ADD})\models_s essay$
, and
$AC(\Pi_2^{\rm ADD})\models_s essay$
, and
![]() $SDA(\Pi_3^{\rm ADD})\models_s \neg\,library$
. This indicates that DC is suppressed but AC and DA are not suppressed, which explains the results of Byrne (Reference Byrne1989).
$SDA(\Pi_3^{\rm ADD})\models_s \neg\,library$
. This indicates that DC is suppressed but AC and DA are not suppressed, which explains the results of Byrne (Reference Byrne1989).
The results of inferences using completion are summarized in Table 2. By the table, the suppression of AC and DA in face of an alternative antecedent is realized in our framework. The suppression of AA and DC in face of an additional antecedent is also realized if the additional condition is written in the antecedent of the original conditional sentence.
Table 2. Summary of inferences made by completion

5.2 Wason selection task
Wason (Reference Wason1968) introduces the selection task for examining human conditional reasoning. The task is described as follows. There are four cards on a table, each of which has a letter on one side and a number on the other. Suppose that those cards are showing respectively D, K, 3, 7. Given the sentence: “Every card which has the letter D on one side has the number 3 on the other side," then which cards are to be turned over in order to verify the truth of the sentence? Testing on college students, it turns out that a relatively small number of students select the logically correct answer “D and 7” (4%), while others select “D and 3” (46%) or D alone (33%) (Wason and Shapiro Reference Wason and Shapiro1971). The result shows that people are likely to perform AC inference but less likely to perform logically correct DC inference in this task. The situation is characterized in our framework as follows.
The sentence: “Every card which has the letter D on one side has the number 3 on the other side" is rephrased as “If a card has the letter D on one side, then it has the number 3 on the other side." Then, it is represented by the program:
where
![]() $n_3$
means the number 3 and
$n_3$
means the number 3 and
![]() $\ell_D$
means the letter D. Four cards on the desk are represented by the facts:
$\ell_D$
means the letter D. Four cards on the desk are represented by the facts:
Then, each card is checked one by one.
•
 $\Pi_W\cup \{\ell_D\leftarrow\}$
has the answer set
$\Pi_W\cup \{\ell_D\leftarrow\}$
has the answer set
 $\{\ell_D, n_3\}$
. If the other side of
$\{\ell_D, n_3\}$
. If the other side of
 $\ell_D$
is not the number 3, however,
$\ell_D$
is not the number 3, however,
 $\{\ell_D, n_3\}\cup\{\neg n_3\}$
is contradictory. To verify the consistency, one has to turn over the card of D.
$\{\ell_D, n_3\}\cup\{\neg n_3\}$
is contradictory. To verify the consistency, one has to turn over the card of D.•
 $\Pi_W\cup \{\ell_K\leftarrow\}$
has the answer set
$\Pi_W\cup \{\ell_K\leftarrow\}$
has the answer set
 $\{\ell_K\}$
. Since both
$\{\ell_K\}$
. Since both
 $\{\ell_K\}\cup\{n_3\}$
and
$\{\ell_K\}\cup\{n_3\}$
and
 $\{\ell_K\}\cup\{\neg n_3\}$
are consistent, there is no need to turn over the card of K.
$\{\ell_K\}\cup\{\neg n_3\}$
are consistent, there is no need to turn over the card of K.•
 $\Pi_W\cup \{n_3\leftarrow\}$
has the answer set
$\Pi_W\cup \{n_3\leftarrow\}$
has the answer set
 $\{n_3\}$
. Since both
$\{n_3\}$
. Since both
 $\{n_3\}\cup\{\ell_D\}$
and
$\{n_3\}\cup\{\ell_D\}$
and
 $\{n_3\}\cup\{\neg \ell_D\}$
are consistent, there is no need to turn over the card of 3.
$\{n_3\}\cup\{\neg \ell_D\}$
are consistent, there is no need to turn over the card of 3.•
 $\Pi_W\cup \{n_7\leftarrow\}$
has the answer set
$\Pi_W\cup \{n_7\leftarrow\}$
has the answer set
 $\{n_7\}$
. Since both
$\{n_7\}$
. Since both
 $\{n_7\}\cup\{\ell_D\}$
and
$\{n_7\}\cup\{\ell_D\}$
and
 $\{n_7\}\cup\{\neg\ell_D\}$
are consistent, there is no need to turn over the card of D.
$\{n_7\}\cup\{\neg\ell_D\}$
are consistent, there is no need to turn over the card of D.
As the standard ASP does not realize DC inference, it characterizes reasoners who select only D as shown above.
By contrast, people who choose D and 3 are likely to perform AC inference using the conditional sentence. In this case, the situation is represented as
Now
![]() $AC(\Pi_W)\cup \{n_3\leftarrow\}$
has the answer set
$AC(\Pi_W)\cup \{n_3\leftarrow\}$
has the answer set
![]() $\{n_3,\ell_D\}$
. If the other side of
$\{n_3,\ell_D\}$
. If the other side of
![]() $n_3$
is not the letter D, however,
$n_3$
is not the letter D, however,
![]() $\{n_3,\ell_D\}\cup\{\neg\ell_D\}$
is contradictory. To verify the consistency, they opt to turn over the card of 3 as well as the card of D.
$\{n_3,\ell_D\}\cup\{\neg\ell_D\}$
is contradictory. To verify the consistency, they opt to turn over the card of 3 as well as the card of D.
Finally, those who choose D and 7 perform weak DC inference asFootnote 4
The program
![]() $\mathit{WDC}(\Pi_W)\cup \{n_7\leftarrow\}$
has the answer set
$\mathit{WDC}(\Pi_W)\cup \{n_7\leftarrow\}$
has the answer set
![]() $\{n_7\}$
. However, if the other side of
$\{n_7\}$
. However, if the other side of
![]() $n_7$
is the letter D,
$n_7$
is the letter D,
![]() $\mathit{WDC}(\Pi_W)\cup \{n_7\leftarrow\}\cup\{ \ell_D\leftarrow\}\cup \{\leftarrow n_3,n_7\}$
is incoherent, where the constraint “
$\mathit{WDC}(\Pi_W)\cup \{n_7\leftarrow\}\cup\{ \ell_D\leftarrow\}\cup \{\leftarrow n_3,n_7\}$
is incoherent, where the constraint “
![]() $\leftarrow n_3, n_7$
" represents that one card cannot have two numbers. To verify the consistency, they need to turn over the card of 7 as well as the card of D.Footnote 5
$\leftarrow n_3, n_7$
" represents that one card cannot have two numbers. To verify the consistency, they need to turn over the card of 7 as well as the card of D.Footnote 5
It is known that the Wason selection task is context dependent and the results change when, for instance, it is presented with a deontic rule. Griggs and Cox (Reference Griggs and Cox1982) use the rule: “If a person is drinking beer, then the person must be over 19 year of age." There are four cards on a table as before, but this time a person’s age is on one side of a card and on the other side is what the person is drinking. Four cards show, “beer,” “coke,” “16,” and “22,” respectively. Then select the card(s) needed to turn over to determine whether or not no person is violating the rule. In this drinking-age problem, almost 75% of participants select logically correct answers “beer” and “16.” To characterize the situation, (W)DC completion is used for representing selection tasks in deontic contexts.
6 Applications to commonsense reasoning
The AC, DC, DA completions realize human conditional reasoning in ASP. In addition, they are used for computing commonsense reasoning in AI.
6.1 Abduction and prediction
Abduction reasons from an observation to explanations. An abductive logic program (Kakas et al. Reference Kakas, Kowalski and Toni1992) is defined as a pair
![]() $\langle\,\Pi,\Gamma\,\rangle$
where
$\langle\,\Pi,\Gamma\,\rangle$
where
![]() $\Pi$
is a program and
$\Pi$
is a program and
![]() $\Gamma\, (\subseteq Lit$
) is a set of literals called abducibles.Footnote 6 It is assumed that abducibles appear in the head of no rule in
$\Gamma\, (\subseteq Lit$
) is a set of literals called abducibles.Footnote 6 It is assumed that abducibles appear in the head of no rule in
![]() $\Pi$
. Given an observation O as a ground literal, the abduction problem is to find an explanation
$\Pi$
. Given an observation O as a ground literal, the abduction problem is to find an explanation
![]() $E\,(\subseteq \Gamma)$
satisfying (i)
$E\,(\subseteq \Gamma)$
satisfying (i)
![]() $\Pi\cup E\models_x O$
and (ii)
$\Pi\cup E\models_x O$
and (ii)
![]() $\Pi\cup E$
is consistent, where
$\Pi\cup E$
is consistent, where
![]() $\models_x$
is either
$\models_x$
is either
![]() $\models_c$
or
$\models_c$
or
![]() $\models_s$
depending on the problem. Here we consider
$\models_s$
depending on the problem. Here we consider
![]() $\models_c$
that realizes credulous abduction. In GEDP, the abduction problem is characterized as follows. Let us define
$\models_c$
that realizes credulous abduction. In GEDP, the abduction problem is characterized as follows. Let us define
Proposition 6.1 (Inoue and Sakama 1998) Let
![]() $\langle\,\Pi,\Gamma\,\rangle$
be an abductive program. Given an observation O, a set
$\langle\,\Pi,\Gamma\,\rangle$
be an abductive program. Given an observation O, a set
![]() $E\subseteq\Gamma$
is an explanation of O iff
$E\subseteq\Gamma$
is an explanation of O iff
![]() $\Pi\cup abd(\Gamma)\cup \{\,\leftarrow not\,O \,\}$
has a consistent answer set S such that
$\Pi\cup abd(\Gamma)\cup \{\,\leftarrow not\,O \,\}$
has a consistent answer set S such that
![]() $S\cap\Gamma=E$
.
$S\cap\Gamma=E$
.
Example 6.1 Consider
![]() $(\Pi_1,\Gamma_1)$
where
$(\Pi_1,\Gamma_1)$
where
 \begin{eqnarray*}\Pi_1:&& arrive\_on\_time\leftarrow not\;accident,\\&& \neg\,arrive\_on\_time\leftarrow accident. \\\Gamma_1:&& accident.\end{eqnarray*}
\begin{eqnarray*}\Pi_1:&& arrive\_on\_time\leftarrow not\;accident,\\&& \neg\,arrive\_on\_time\leftarrow accident. \\\Gamma_1:&& accident.\end{eqnarray*}
![]() $\Pi_1$
represents that a train arrives on time unless there is an accident. Given the observation
$\Pi_1$
represents that a train arrives on time unless there is an accident. Given the observation
![]() $O=\neg\,arrive\_on\_time$
, it has the explanation
$O=\neg\,arrive\_on\_time$
, it has the explanation
![]() $E=\{accident\}$
. The problem is represented as the GEDP:
$E=\{accident\}$
. The problem is represented as the GEDP:
 \begin{eqnarray*}&& arrive\_on\_time\leftarrow not\;accident,\\&& \neg\,arrive\_on\_time\leftarrow accident, \\&& accident\,;\, not\,accident\leftarrow,\\&& \leftarrow not\,\neg\,arrive\_on\_time\end{eqnarray*}
\begin{eqnarray*}&& arrive\_on\_time\leftarrow not\;accident,\\&& \neg\,arrive\_on\_time\leftarrow accident, \\&& accident\,;\, not\,accident\leftarrow,\\&& \leftarrow not\,\neg\,arrive\_on\_time\end{eqnarray*}
which has the answer set
![]() $S=\{ \neg\,arrive\_on\_time,\; accident \}$
where
$S=\{ \neg\,arrive\_on\_time,\; accident \}$
where
![]() $S\cap\Gamma_1=E$
.
$S\cap\Gamma_1=E$
.
Since abduction reasons backward from an observation, it is characterized using AC inference as follows.
Proposition 6.2 Let
![]() $\langle\,\Pi,\Gamma\,\rangle$
be an abductive program and O an observation.
$\langle\,\Pi,\Gamma\,\rangle$
be an abductive program and O an observation.
(i) A set
 $E\subseteq\Gamma$
is an explanation of O if
$E\subseteq\Gamma$
is an explanation of O if
 $O\in head^+(r)$
for some
$O\in head^+(r)$
for some
 $r\in\Pi$
and
$r\in\Pi$
and
 $AC(\Pi)\cup \{ O\}$
has a consistent answer set S such that
$AC(\Pi)\cup \{ O\}$
has a consistent answer set S such that
 $S\cap\Gamma=E$
.
$S\cap\Gamma=E$
.(ii) If a set
 $E\subseteq\Gamma$
is an explanation of O, then there is
$E\subseteq\Gamma$
is an explanation of O, then there is
 $\Pi'\subseteq\Pi$
such that
$\Pi'\subseteq\Pi$
such that
 $AC(\Pi')\cup \{ O\}$
has a consistent answer set S such that
$AC(\Pi')\cup \{ O\}$
has a consistent answer set S such that
 $S\cap\Gamma=E$
.
$S\cap\Gamma=E$
.
(i) Suppose that
 $O\in head^+(r)$
for some
$O\in head^+(r)$
for some
 $r\in\Pi$
and
$r\in\Pi$
and
 $AC(\Pi)\cup \{ O\}$
has a consistent answer set S such that
$AC(\Pi)\cup \{ O\}$
has a consistent answer set S such that
 $S\cap\Gamma=E$
. By the definition of
$S\cap\Gamma=E$
. By the definition of
 $AC(\Pi)$
, there is a path from O to literals in E in the dependency graphFootnote 7 of the program
$AC(\Pi)$
, there is a path from O to literals in E in the dependency graphFootnote 7 of the program
 $AC(\Pi)^S\cup\{O\}$
where
$AC(\Pi)^S\cup\{O\}$
where
 $AC(\Pi)^S$
is the reduct of
$AC(\Pi)^S$
is the reduct of
 $AC(\Pi)$
by S. In this case, O is reached by reasoning forward from E in
$AC(\Pi)$
by S. In this case, O is reached by reasoning forward from E in
 $\Pi^S$
, and S is an answer set of
$\Pi^S$
, and S is an answer set of
 $\Pi^S\cup E$
such that
$\Pi^S\cup E$
such that
 $O\in S$
. This implies that
$O\in S$
. This implies that
 $\Pi\cup E\cup\{\leftarrow not\,O\}$
has a consistent answer set S such that
$\Pi\cup E\cup\{\leftarrow not\,O\}$
has a consistent answer set S such that
 $abd(\Gamma)^S=E$
, and the result holds by Proposition 6.1
$abd(\Gamma)^S=E$
, and the result holds by Proposition 6.1(ii) If
 $E\subseteq\Gamma$
is an explanation of O, there is
$E\subseteq\Gamma$
is an explanation of O, there is
 $\Pi'\subseteq\Pi$
such that
$\Pi'\subseteq\Pi$
such that
 $\Pi'\cup abd(\Gamma)\cup\{\leftarrow not\,O\}$
has a consistent answer set S satisfying
$\Pi'\cup abd(\Gamma)\cup\{\leftarrow not\,O\}$
has a consistent answer set S satisfying
 $S\cap\Gamma=E$
(Proposition 6.1). Select a minimal set
$S\cap\Gamma=E$
(Proposition 6.1). Select a minimal set
 $\Pi'$
of rules such that there is no
$\Pi'$
of rules such that there is no
 $\Pi''\subset\Pi'$
satisfying the above condition. In this case,
$\Pi''\subset\Pi'$
satisfying the above condition. In this case,
 $abd(\Gamma)^S=E$
is obtained by reasoning backward from O in
$abd(\Gamma)^S=E$
is obtained by reasoning backward from O in
 $(\Pi')^S$
, and S is a minimal set satisfying
$(\Pi')^S$
, and S is a minimal set satisfying
 $(\Pi')^S\cup ac(\Pi')^S\cup\{O\}$
. Then,
$(\Pi')^S\cup ac(\Pi')^S\cup\{O\}$
. Then,
 $AC(\Pi')\cup \{ O\}$
has a consistent answer set S such that
$AC(\Pi')\cup \{ O\}$
has a consistent answer set S such that
 $S\cap\Gamma=E$
.
$S\cap\Gamma=E$
.
In Example 6.1,
![]() $AC(\Pi_1)\cup \{ O\}$
becomes
$AC(\Pi_1)\cup \{ O\}$
becomes
 \begin{eqnarray*}&& not\;accident\leftarrow arrive\_on\_time,\\&& accident\leftarrow \neg\,arrive\_on\_time,\\&& \neg\,arrive\_on\_time \leftarrow,\end{eqnarray*}
\begin{eqnarray*}&& not\;accident\leftarrow arrive\_on\_time,\\&& accident\leftarrow \neg\,arrive\_on\_time,\\&& \neg\,arrive\_on\_time \leftarrow,\end{eqnarray*}
which has the answer set
![]() $S=\{\, \neg\,arrive\_on\_time,\, accident\,\}$
. By
$S=\{\, \neg\,arrive\_on\_time,\, accident\,\}$
. By
![]() $S\cap\Gamma_1=\{\,accident\,\}$
,
$S\cap\Gamma_1=\{\,accident\,\}$
,
![]() $E=\{\,accident\,\}$
is the explanation.
$E=\{\,accident\,\}$
is the explanation.
Note that
![]() $AC(\Pi)$
introduces converse of every rule, while explanations are computed using the AC completion of a subset
$AC(\Pi)$
introduces converse of every rule, while explanations are computed using the AC completion of a subset
![]() $\Pi'\subseteq \Pi$
in general (Proposition 6.2(ii)).
$\Pi'\subseteq \Pi$
in general (Proposition 6.2(ii)).
Example 6.2 Let
![]() $\Pi=\{\, p\leftarrow a,\;\; q\leftarrow \neg a,\;\; q\leftarrow\,\}$
and
$\Pi=\{\, p\leftarrow a,\;\; q\leftarrow \neg a,\;\; q\leftarrow\,\}$
and
![]() $\Gamma=\{a,\neg a\}$
. Then
$\Gamma=\{a,\neg a\}$
. Then
![]() $O=p$
has the explanation
$O=p$
has the explanation
![]() $E=\{a\}$
in
$E=\{a\}$
in
![]() $\langle\,\Pi,\Gamma\,\rangle$
, while
$\langle\,\Pi,\Gamma\,\rangle$
, while
![]() $AC(\Pi)\cup\{O\}=\Pi\cup\{\, a\leftarrow p,\;\; \neg a\leftarrow q,\;\; p\leftarrow\,\}$
is contradictory. By putting
$AC(\Pi)\cup\{O\}=\Pi\cup\{\, a\leftarrow p,\;\; \neg a\leftarrow q,\;\; p\leftarrow\,\}$
is contradictory. By putting
![]() $\Pi'=\{\, p\leftarrow a\,\}$
,
$\Pi'=\{\, p\leftarrow a\,\}$
,
![]() $AC(\Pi')\cup\{O\}$
has the consistent answer set
$AC(\Pi')\cup\{O\}$
has the consistent answer set
![]() $S=\{p,a\}$
where
$S=\{p,a\}$
where
![]() $S\cap\Gamma=\{a\}$
.
$S\cap\Gamma=\{a\}$
.
As illustrated in Example 6.2, abduction and AC completion produce different results in general.
Abductive logic programs of Kakas et al. (Reference Kakas, Kowalski and Toni1992) cannot compute explanations when contrary to the consequent is observed. For instance, consider
![]() $\langle\,\Pi_2,\Gamma_2\,\rangle$
such that
$\langle\,\Pi_2,\Gamma_2\,\rangle$
such that
Given the observation
![]() $O=\neg\,arrive\_on\_time$
, no explanation is obtained from
$O=\neg\,arrive\_on\_time$
, no explanation is obtained from
![]() $\langle\,\Pi_2,\Gamma_2\,\rangle$
. Generally, a program
$\langle\,\Pi_2,\Gamma_2\,\rangle$
. Generally, a program
![]() $\Pi$
does not necessarily contain a pair of rules r and r’ that define L and
$\Pi$
does not necessarily contain a pair of rules r and r’ that define L and
![]() $\neg L$
, respectively. When there is a rule defining L but no rule defining
$\neg L$
, respectively. When there is a rule defining L but no rule defining
![]() $\neg L$
, abduction computes no explanation for the observation
$\neg L$
, abduction computes no explanation for the observation
![]() $O=\neg L$
. The problem is resolved by reasoning by DC. For the rule r in
$O=\neg L$
. The problem is resolved by reasoning by DC. For the rule r in
![]() $\Pi_2$
, sdc(r) becomes
$\Pi_2$
, sdc(r) becomes
Then,
![]() $SDC(\Pi_2)\cup\{O\}$
computes the explanation
$SDC(\Pi_2)\cup\{O\}$
computes the explanation
![]() $\{\,accident\,\}$
.
$\{\,accident\,\}$
.
In contrast to SDC, WDC is used for abduction from negative observations. A negative observation represents that some evidence G is not observed, and it is represented as
![]() $O=not\,G$
, which should be distinguished from the (positive) observation
$O=not\,G$
, which should be distinguished from the (positive) observation
![]() $O=\neg\,G$
meaning that
$O=\neg\,G$
meaning that
![]() $\neg\,G$
is observed. In the abductive program
$\neg\,G$
is observed. In the abductive program
![]() $\langle\,\Pi_2,\Gamma_2\,\rangle$
, the negative observation
$\langle\,\Pi_2,\Gamma_2\,\rangle$
, the negative observation
![]() $O=not\,arrive\_on\_time$
is explained using wdc(r):
$O=not\,arrive\_on\_time$
is explained using wdc(r):
Then,
![]() $WDC(\Pi_2)\cup\{O\}$
has the answer set
$WDC(\Pi_2)\cup\{O\}$
has the answer set
![]() $\{\,accident\,\}$
.
$\{\,accident\,\}$
.
In this way, both AC and DC are used for computing explanations deductively, and DC is used for computing explanations that are not obtained using the framework of Kakas et al. (Reference Kakas, Kowalski and Toni1992). Moreover, AC and DC realize prediction by combining abduction and deduction.
Example 6.3 Consider
![]() $(\Pi_3,\Gamma_3)$
where
$(\Pi_3,\Gamma_3)$
where
 \begin{eqnarray*}\Pi_3:&& arrive\_on\_time\leftarrow not\;accident,\\&& \neg\,arrive\_on\_time\leftarrow accident, \\&& newspaper \leftarrow accident.\\\Gamma_3:&& accident.\end{eqnarray*}
\begin{eqnarray*}\Pi_3:&& arrive\_on\_time\leftarrow not\;accident,\\&& \neg\,arrive\_on\_time\leftarrow accident, \\&& newspaper \leftarrow accident.\\\Gamma_3:&& accident.\end{eqnarray*}
The third rule in
![]() $\Pi_3$
says: if there is an accident, a newspaper will report it. Given the observation
$\Pi_3$
says: if there is an accident, a newspaper will report it. Given the observation
![]() $O=\neg\,arrive\_on\_time$
,
$O=\neg\,arrive\_on\_time$
,
![]() $AC(\Pi_3)\cup \{ O\}\models_s newspaper$
.
$AC(\Pi_3)\cup \{ O\}\models_s newspaper$
.
As such, AC or DC combines abduction and deduction to realize prediction.
6.2 Counterfactual reasoning
A counterfactual is a conditional statement representing what would be the case if its premise were true (although it is not true in fact). Lewis (Reference Lewis1973) introduces two different types of counterfactual sentences. Given two different events
![]() ${\varphi}$
and
${\varphi}$
and
![]() $\psi$
, two counterfactual sentences are considered: “if it were the case that
$\psi$
, two counterfactual sentences are considered: “if it were the case that
![]() ${\varphi}$
, then it would be the case that
${\varphi}$
, then it would be the case that
![]() $\psi$
" (written
$\psi$
" (written
![]() ${\varphi}\,\Box\!\!\!\rightarrow\,\psi$
) and “if it were the case that
${\varphi}\,\Box\!\!\!\rightarrow\,\psi$
) and “if it were the case that
![]() ${\varphi}$
, then it might be the case that
${\varphi}$
, then it might be the case that
![]() $\psi$
" (written
$\psi$
" (written
![]() ${\varphi}\,\Diamond\!\!\!\rightarrow\,\psi$
). Here
${\varphi}\,\Diamond\!\!\!\rightarrow\,\psi$
). Here
![]() $({\varphi}\,\Box\!\!\!\rightarrow\,\psi)$
implies
$({\varphi}\,\Box\!\!\!\rightarrow\,\psi)$
implies
![]() $({\varphi}\,\Diamond\!\!\!\rightarrow\,\psi)$
. We consider counterfactual reasoning such that what would be the case if some facts were not true. We then realize Lewis’s two types of counterfactual reasoning using DA inference in ASP.
$({\varphi}\,\Diamond\!\!\!\rightarrow\,\psi)$
. We consider counterfactual reasoning such that what would be the case if some facts were not true. We then realize Lewis’s two types of counterfactual reasoning using DA inference in ASP.
Definition 6.1 (counterfact) Let
![]() ${\varphi}$
be a fact of the form:
${\varphi}$
be a fact of the form:
Then, the counterfact
![]() $\overline{{\varphi}}$
is the set of facts such that
$\overline{{\varphi}}$
is the set of facts such that
Given a set
![]() $\Sigma$
of facts, define
$\Sigma$
of facts, define
We say that
![]() $\overline{\Sigma}$
satisfies the conjunction “
$\overline{\Sigma}$
satisfies the conjunction “
![]() $L_{l+1},\,\ldots,\,L_m,\,not\,L_{m+1},\,\ldots,\,not\,L_n$
" if
$L_{l+1},\,\ldots,\,L_m,\,not\,L_{m+1},\,\ldots,\,not\,L_n$
" if
![]() $\{\, L_i\leftarrow \,\mid\, l+1\le i\le m\}\subseteq\overline{\Sigma}$
and
$\{\, L_i\leftarrow \,\mid\, l+1\le i\le m\}\subseteq\overline{\Sigma}$
and
![]() $\{\, L_j\leftarrow \,\mid\, m+1\le i\le n\}\cap\overline{\Sigma}={\varnothing}$
.
$\{\, L_j\leftarrow \,\mid\, m+1\le i\le n\}\cap\overline{\Sigma}={\varnothing}$
.
Definition 6.2 (counterfactual program) Let
![]() $\Pi$
be a program and
$\Pi$
be a program and
![]() $\Sigma$
a set of facts in
$\Sigma$
a set of facts in
![]() $\Pi$
. Then, a counterfactual program
$\Pi$
. Then, a counterfactual program
![]() $\Omega$
is defined as
$\Omega$
is defined as
For
![]() $\lambda\in Lit$
, define
$\lambda\in Lit$
, define
By definition,
![]() $\Omega$
is obtained from
$\Omega$
is obtained from
![]() $\Pi$
by removing a set
$\Pi$
by removing a set
![]() $\Sigma$
of facts, and instead introducing a set
$\Sigma$
of facts, and instead introducing a set
![]() $\overline{\Sigma}$
of counterfacts as well as strong DA rules
$\overline{\Sigma}$
of counterfacts as well as strong DA rules
![]() $sda(\Pi)$
.
$sda(\Pi)$
.
![]() $\overline{\Sigma}\;\Box\!\!\!\rightarrow\,\lambda$
(resp.
$\overline{\Sigma}\;\Box\!\!\!\rightarrow\,\lambda$
(resp.
![]() $\overline{\Sigma}\;\Diamond\!\!\!\rightarrow\,\lambda$
) means that if the counterfacts
$\overline{\Sigma}\;\Diamond\!\!\!\rightarrow\,\lambda$
) means that if the counterfacts
![]() $\overline{\Sigma}$
were the case, then
$\overline{\Sigma}$
were the case, then
![]() $\lambda$
is included in every (resp. some) answer set of
$\lambda$
is included in every (resp. some) answer set of
![]() $\Omega$
.
$\Omega$
.
Example 6.4 Consider the program
![]() $\Pi$
:
$\Pi$
:
 \begin{eqnarray*}&& London\,;\,Paris \leftarrow not\; virtual,\\&& virtual\leftarrow pandemic,\\&& pandemic \leftarrow.\end{eqnarray*}
\begin{eqnarray*}&& London\,;\,Paris \leftarrow not\; virtual,\\&& virtual\leftarrow pandemic,\\&& pandemic \leftarrow.\end{eqnarray*}
An event is scheduled to take place in either London or Paris if it is not virtual. The pandemic turns the event into virtual, however. Suppose a counterfactual sentence: “ if there were no pandemic, the event would not be virtual." Putting
![]() $\Sigma=\{\,pandemic\,\}$
,
$\Sigma=\{\,pandemic\,\}$
,
![]() $\Omega$
becomes:
$\Omega$
becomes:
 \begin{eqnarray*}&& London\,;\,Paris \leftarrow not\; virtual,\\&& virtual\leftarrow pandemic,\\&& \neg\,London\leftarrow virtual,\\&& \neg\,Paris\leftarrow virtual,\\&& \neg\,virtual\leftarrow \neg\,pandemic,\\&& \neg\,pandemic \leftarrow.\end{eqnarray*}
\begin{eqnarray*}&& London\,;\,Paris \leftarrow not\; virtual,\\&& virtual\leftarrow pandemic,\\&& \neg\,London\leftarrow virtual,\\&& \neg\,Paris\leftarrow virtual,\\&& \neg\,virtual\leftarrow \neg\,pandemic,\\&& \neg\,pandemic \leftarrow.\end{eqnarray*}
Then,
![]() $\Omega$
has two answer sets:
$\Omega$
has two answer sets:
As a result, it holds that
Given a consistent program
![]() $\Pi$
, it might be the case that the program
$\Pi$
, it might be the case that the program
![]() $\Omega$
is inconsistent. To eliminate contradictory
$\Omega$
is inconsistent. To eliminate contradictory
![]() $\Omega$
, default DA completion is used instead of DA completion. Define
$\Omega$
, default DA completion is used instead of DA completion. Define
![]() $\Omega_D$
that is obtained by replacing
$\Omega_D$
that is obtained by replacing
![]() $sda(\Pi)$
by its default version
$sda(\Pi)$
by its default version
![]() $sdda(\Pi)$
in Definition 6.2. The next result holds by Proposition 4.4.
$sdda(\Pi)$
in Definition 6.2. The next result holds by Proposition 4.4.
Proposition 6.3 Let
![]() $\Pi$
be an EDP and
$\Pi$
be an EDP and
![]() $\Sigma$
a set of facts in
$\Sigma$
a set of facts in
![]() $\Pi$
. If
$\Pi$
. If
![]() $(\Pi\setminus\Sigma)\,\cup\,\overline{\Sigma}$
is consistent, then
$(\Pi\setminus\Sigma)\,\cup\,\overline{\Sigma}$
is consistent, then
![]() $\Omega_D$
is not contradictory.
$\Omega_D$
is not contradictory.
Proof. Put
![]() $\Pi'=(\Pi\setminus\Sigma)\,\cup\,\overline{\Sigma}$
. Since facts are set aside in (SD)DA completion,
$\Pi'=(\Pi\setminus\Sigma)\,\cup\,\overline{\Sigma}$
. Since facts are set aside in (SD)DA completion,
![]() $\Omega_D=\Pi'\cup sdda(\Pi)=\Pi'\cup sdda(\Pi')=SDDA(\Pi')$
. Suppose that
$\Omega_D=\Pi'\cup sdda(\Pi)=\Pi'\cup sdda(\Pi')=SDDA(\Pi')$
. Suppose that
![]() $SDDA(\Pi')$
has the answer set Lit. Then
$SDDA(\Pi')$
has the answer set Lit. Then
![]() $\Pi'$
has the answer set Lit (Proposition 4.4). Since
$\Pi'$
has the answer set Lit (Proposition 4.4). Since
![]() $\Pi'$
is an EDP,
$\Pi'$
is an EDP,
![]() $\Pi'$
is inconsistent, which contradicts the assumption that
$\Pi'$
is inconsistent, which contradicts the assumption that
![]() $\Pi'$
is consistent. Hence, the result holds.
$\Pi'$
is consistent. Hence, the result holds.
6.3 Neighborhood inference
Cooperative query answering analyzes the intent of a query and provides associated information relevant to the query (Chu et al. Reference Chu, Chen and Lee1990). Neighborhood inference (Gaasterland et al. Reference Gaasterland, Godfrey and Minker1992) is a technique used for such a purpose and reasons up/down in a taxonomy of atoms to reach neighboring solutions.
Example 6.5 A travel agency has flight information represented by the program
![]() $\Pi$
:
$\Pi$
:
 \begin{eqnarray*}&& travel(LHR,CDG)\leftarrow flight(AF1681),\\&& travel(LHR,CDG)\leftarrow flight(BA306),\\&& travel(NRT,CDG)\leftarrow flight(AF275),\\&& flight(BA306)\leftarrow,\;\;\; \neg\,flight(AF1681)\leftarrow,\;\;\;flight(AF275)\leftarrow\end{eqnarray*}
\begin{eqnarray*}&& travel(LHR,CDG)\leftarrow flight(AF1681),\\&& travel(LHR,CDG)\leftarrow flight(BA306),\\&& travel(NRT,CDG)\leftarrow flight(AF275),\\&& flight(BA306)\leftarrow,\;\;\; \neg\,flight(AF1681)\leftarrow,\;\;\;flight(AF275)\leftarrow\end{eqnarray*}
where “
![]() $travel(X,Y)\leftarrow flight(Z)$
" means that a flight Z is used for traveling from X to Y. Suppose that a customer asks the availability of a flight AF1681 from LHR to CDG. Unfortunately, no ticket is available on the requested time of a day. The agent then proposes an alternative flight BA306 that is still available.
$travel(X,Y)\leftarrow flight(Z)$
" means that a flight Z is used for traveling from X to Y. Suppose that a customer asks the availability of a flight AF1681 from LHR to CDG. Unfortunately, no ticket is available on the requested time of a day. The agent then proposes an alternative flight BA306 that is still available.
In this scenario, from the request flight(AF1681) the agent understands that the customer wants to travel from London (LHR) to Paris (CDG). The request flight(AF1681) is then relaxed to travel(LHR,CDG) and reaches the fact flight(BA306).
Neighborhood inference consists of two steps: generalization from the body to the head of one rule and specialization from the head to the body of another rule. The generalization is the inference of affirming the antecedent, while the specialization is the inference of affirming the consequent. Then, neighborhood inference is realized by combining AA and AC. In what follows, we consider a binary program
![]() $\Pi$
that consists of ground rules of the form “
$\Pi$
that consists of ground rules of the form “
![]() $L_1\leftarrow L_2$
" where
$L_1\leftarrow L_2$
" where
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are positive/negative literals (
$L_2$
are positive/negative literals (
![]() $L_2$
is possibly empty).
$L_2$
is possibly empty).
![]() $\Pi$
is partitioned into the set of non-factual rules
$\Pi$
is partitioned into the set of non-factual rules
![]() $\Pi_R$
and the set of facts
$\Pi_R$
and the set of facts
![]() $\Pi_F$
, that is,
$\Pi_F$
, that is,
![]() $\Pi=\Pi_R\cup\Pi_F$
.
$\Pi=\Pi_R\cup\Pi_F$
.
Definition 6.3 (neighborhood solution) Let
![]() $\Pi$
be a binary program such that
$\Pi$
be a binary program such that
![]() $\Pi=\Pi_R\cup \Pi_F$
and G a ground literal representing a request. Define
$\Pi=\Pi_R\cup \Pi_F$
and G a ground literal representing a request. Define
If U and V are non-empty and
![]() $\Pi_R\cup ac(V)\cup \{G\}$
has a consistent answer set S, then
$\Pi_R\cup ac(V)\cup \{G\}$
has a consistent answer set S, then
![]() $S\cap \Pi_F$
is called a neighborhood solution of G.
$S\cap \Pi_F$
is called a neighborhood solution of G.
By definition, the AC completion is applied to a part of the program, which realizes neighborhood inference based on a request.
Example 6.6 (cont. Example 6.5) Given the request
![]() $G=flight(AF1681)$
,
$G=flight(AF1681)$
,
![]() $U=\{\, travel(LHR,CDG)\leftarrow flight(AF1681) \,\}$
and
$U=\{\, travel(LHR,CDG)\leftarrow flight(AF1681) \,\}$
and
![]() $V=\{\, travel(LHR,CDG)\leftarrow flight(BA306) \,\}$
. Then,
$V=\{\, travel(LHR,CDG)\leftarrow flight(BA306) \,\}$
. Then,
![]() $ac(V)=\{\,flight(BA306)\leftarrow travel(LHR,CDG)\,\}$
, and
$ac(V)=\{\,flight(BA306)\leftarrow travel(LHR,CDG)\,\}$
, and
![]() $\Pi_R\cup ac(V)$
becomes
$\Pi_R\cup ac(V)$
becomes
 \begin{eqnarray*}&& travel(LHR,CDG)\leftarrow flight(AF1681),\\&& travel(LHR,CDG)\leftarrow flight(BA306),\\&& travel(NRT,CDG)\leftarrow flight(AF275),\\&& flight(BA306) \leftarrow travel(LHR,CDG).\end{eqnarray*}
\begin{eqnarray*}&& travel(LHR,CDG)\leftarrow flight(AF1681),\\&& travel(LHR,CDG)\leftarrow flight(BA306),\\&& travel(NRT,CDG)\leftarrow flight(AF275),\\&& flight(BA306) \leftarrow travel(LHR,CDG).\end{eqnarray*}
![]() $\Pi_R\cup ac(V)\cup \{G\}$
has the answer set
$\Pi_R\cup ac(V)\cup \{G\}$
has the answer set
Hence,
![]() $S\cap \Pi_F=\{ flight(BA306) \}$
is a neighborhood solution of G.
$S\cap \Pi_F=\{ flight(BA306) \}$
is a neighborhood solution of G.
Proposition 6.4 Let
![]() $\Pi$
be a binary program and G a ground literal representing a request. If U and V in Definition 6.3 are non-empty and
$\Pi$
be a binary program and G a ground literal representing a request. If U and V in Definition 6.3 are non-empty and
![]() $AC(\Pi)\cup\{G\}$
is consistent, G has a neighborhood solution.
$AC(\Pi)\cup\{G\}$
is consistent, G has a neighborhood solution.
Proof. Since
![]() $\Pi_R\cup ac(V)\subseteq AC(\Pi)$
,
$\Pi_R\cup ac(V)\subseteq AC(\Pi)$
,
![]() $\Pi_R\cup ac(V)\cup \{G\}$
has a consistent answer set S. In this case, G has a neighborhood solution
$\Pi_R\cup ac(V)\cup \{G\}$
has a consistent answer set S. In this case, G has a neighborhood solution
![]() $S\cap \Pi_F$
.
$S\cap \Pi_F$
.
7 Related work
There is a number of studies on human conditional reasoning in psychology and cognitive science. In this section, we focus on related work based on logic programming and its application to common sense reasoning.
7.1 Completion
The idea of interpreting if-then rules in logic programs as bi-conditional dates back to Clark (Reference Clark and Press1978). He introduces predicate completion in normal logic programs (NLPs), which introduces the only-if part of each rule to a program. Given a propositional NLP
![]() $\Pi$
, Clark completion
$\Pi$
, Clark completion
![]() $Comp(\Pi)$
is obtained by two steps: (i) all rules “
$Comp(\Pi)$
is obtained by two steps: (i) all rules “
![]() $p\leftarrow B_1$
",
$p\leftarrow B_1$
",
![]() $\ldots$
, “
$\ldots$
, “
![]() $p\leftarrow B_k$
" in
$p\leftarrow B_k$
" in
![]() $\Pi$
having the same head p are replaced by “
$\Pi$
having the same head p are replaced by “
![]() $p\leftrightarrow B_1\vee\cdots\vee B_k,$
" where
$p\leftrightarrow B_1\vee\cdots\vee B_k,$
" where
![]() $B_i$
$B_i$
![]() $(1\le i\le k)$
is a conjunction of literals; and (ii) for any atom p appearing in the head of no rule in
$(1\le i\le k)$
is a conjunction of literals; and (ii) for any atom p appearing in the head of no rule in
![]() $\Pi$
, add “
$\Pi$
, add “
![]() $p\leftrightarrow \mathit{false.}$
" The AC completion introduced in this paper extends the technique to the class of GEDP, while the result is generally different from Clark completion in NLPs. For instance, given the program:
$p\leftrightarrow \mathit{false.}$
" The AC completion introduced in this paper extends the technique to the class of GEDP, while the result is generally different from Clark completion in NLPs. For instance, given the program:
Clark completion becomes
where
![]() $\top$
and
$\top$
and
![]() $\bot$
represent true and false, respectively.
$\bot$
represent true and false, respectively.
![]() $Comp(\Pi_1)$
has the single completion model called a supported model (Apt et al. Reference Apt, Blair, Walker and Kaufmann1988)
$Comp(\Pi_1)$
has the single completion model called a supported model (Apt et al. Reference Apt, Blair, Walker and Kaufmann1988)
![]() $\{p\}$
. In contrast,
$\{p\}$
. In contrast,
has the answer set
![]() $\{p,q\}$
. The difference comes from the fact that in
$\{p,q\}$
. The difference comes from the fact that in
![]() $Comp(\Pi_1)$
, q is identified with false but this is not the case in
$Comp(\Pi_1)$
, q is identified with false but this is not the case in
![]() $AC(\Pi_1)$
. In Clark completion, undefined atoms (i.e. atoms appearing in the head of no rule) are interpreted false. We do not use this type of completion because it disturbs the basic type of AC reasoning that infers q from p and “
$AC(\Pi_1)$
. In Clark completion, undefined atoms (i.e. atoms appearing in the head of no rule) are interpreted false. We do not use this type of completion because it disturbs the basic type of AC reasoning that infers q from p and “
![]() $p\leftarrow q$
." Clark completion is extended to normal disjunctive programs by several researchers (Lobo et al. Reference Lobo, Minker, Rajasekar, Press and Cambridge1988; Alviano and Dodaro Reference Alviano and Dodaro2016; Nieves and Osorio Reference Nieves and Osorio2018).Those extensions reduce to Clark completion in NLPs, so that they are different from the AC completion. We also introduce the DC completion and the DA completion. When
$p\leftarrow q$
." Clark completion is extended to normal disjunctive programs by several researchers (Lobo et al. Reference Lobo, Minker, Rajasekar, Press and Cambridge1988; Alviano and Dodaro Reference Alviano and Dodaro2016; Nieves and Osorio Reference Nieves and Osorio2018).Those extensions reduce to Clark completion in NLPs, so that they are different from the AC completion. We also introduce the DC completion and the DA completion. When
![]() $\Pi_2=\{\, p\leftarrow not\,q\,\}$
,
$\Pi_2=\{\, p\leftarrow not\,q\,\}$
,
![]() $Comp(\Pi_2)=\{\, p\leftrightarrow \neg q,\;\; q\leftrightarrow\bot \,\}$
has the supported model
$Comp(\Pi_2)=\{\, p\leftrightarrow \neg q,\;\; q\leftrightarrow\bot \,\}$
has the supported model
![]() $\{p\}$
. On the other hand,
$\{p\}$
. On the other hand,
has two answer sets
![]() $\{p\}$
and
$\{p\}$
and
![]() $\{q\}$
. When
$\{q\}$
. When
![]() $\Pi_3=\{\, p\leftarrow not\,q,\;\; p\leftarrow q,\;\; q\leftarrow p\,\}$
,
$\Pi_3=\{\, p\leftarrow not\,q,\;\; p\leftarrow q,\;\; q\leftarrow p\,\}$
,
![]() $Comp(\Pi_3)=\{\, p\leftrightarrow q\vee\neg q,\;\; q\leftrightarrow p\,\}$
has the supported model
$Comp(\Pi_3)=\{\, p\leftrightarrow q\vee\neg q,\;\; q\leftrightarrow p\,\}$
has the supported model
![]() $\{p,q\}$
. In contrast,
$\{p,q\}$
. In contrast,
has no answer set. As such, completion semantics introduced in this paper is generally different from Clark completion in NLPs.
The weak completion (Hölldobler and Kencana Ramli Reference Hölldobler and Kencana Ramli2009) leaves undefined atoms unknown under 3-valued logic. In the program
![]() $\Pi_1=\{\, p\leftarrow q,\;\; p\leftarrow \,\}$
, the weak completion becomes
$\Pi_1=\{\, p\leftarrow q,\;\; p\leftarrow \,\}$
, the weak completion becomes
which is semantically equivalent to
![]() $\{\, p\leftrightarrow \top \,\}$
. Then, p is true but q is unknown in
$\{\, p\leftrightarrow \top \,\}$
. Then, p is true but q is unknown in
![]() $wcomp(\Pi_1)$
, which is again different from
$wcomp(\Pi_1)$
, which is again different from
![]() $AC(\Pi_1)$
that has the answer set
$AC(\Pi_1)$
that has the answer set
![]() $\{p,q\}$
. In the program
$\{p,q\}$
. In the program
![]() $\Pi_2=\{\, p\leftarrow not\,q\,\}$
, the weak completion becomes
$\Pi_2=\{\, p\leftarrow not\,q\,\}$
, the weak completion becomes
then both p and q are unknown. In contrast,
![]() $WDC(\Pi_2)$
has two answer sets
$WDC(\Pi_2)$
has two answer sets
![]() $\{p\}$
and
$\{p\}$
and
![]() $\{q\}$
, and
$\{q\}$
, and
![]() $WDA(\Pi_2)$
has the single answer set
$WDA(\Pi_2)$
has the single answer set
![]() $\{p\}$
.
$\{p\}$
.
7.2 Human conditional reasoning
Stenning and Lambalgen (2008) formulate human conditional reasoning using Clark’s program completion under the three-valued logic of Fitting (Reference Fitting1985). They represent a conditional sentence “if p then q" as a logic programming rule:Footnote 8
where ab represents an abnormal atom. In this setting, DA is represented as
The rule “
![]() $A\leftarrow\bot$
" means that A is a proposition to which the closed world assumption (Reiter Reference Reiter and Press1978) is applied. If a program does not contain “
$A\leftarrow\bot$
" means that A is a proposition to which the closed world assumption (Reiter Reference Reiter and Press1978) is applied. If a program does not contain “
![]() $A\leftarrow\bot,$
" nor any other rule in which A occurs in its head, then A is interpreted unknown. Then, its completion
$A\leftarrow\bot,$
" nor any other rule in which A occurs in its head, then A is interpreted unknown. Then, its completion
derives “
![]() $q\leftrightarrow\bot$
." On the other hand, completion does not realize AC or DC inference by itself. In their framework, AC is represented as
$q\leftrightarrow\bot$
." On the other hand, completion does not realize AC or DC inference by itself. In their framework, AC is represented as
while its completion
does not derive p. Likewise, DC is represented as
while its completion
does not derive “
![]() $p\leftrightarrow\bot$
." They then interpret “
$p\leftrightarrow\bot$
." They then interpret “
![]() $q\leftarrow p\wedge\neg ab$
" as an integrity constraint meaning that “if q succeeds (resp. fails) then “
$q\leftarrow p\wedge\neg ab$
" as an integrity constraint meaning that “if q succeeds (resp. fails) then “
![]() $p\wedge\neg ab$
” succeeds (resp. fails)" to get the AC consequence p (resp. DC consequence
$p\wedge\neg ab$
” succeeds (resp. fails)" to get the AC consequence p (resp. DC consequence
![]() $\neg p$
).
$\neg p$
).
Stenning and Lambalgen (2008) characterize the suppression task in their formulation. The sentence “If she has an essay to write then she will study late in the library" is represented as:
Given the negation of antecedent
![]() $\neg essay$
(or equivalently, the CWA rule “
$\neg essay$
(or equivalently, the CWA rule “
![]() $essay\leftarrow\bot$
"), the completed program:
$essay\leftarrow\bot$
"), the completed program:
 \begin{eqnarray*} && library\;\leftrightarrow essay\wedge \neg ab_1,\\ && ab_1\leftrightarrow\bot,\\ && essay\leftrightarrow\bot\end{eqnarray*}
\begin{eqnarray*} && library\;\leftrightarrow essay\wedge \neg ab_1,\\ && ab_1\leftrightarrow\bot,\\ && essay\leftrightarrow\bot\end{eqnarray*}
derives “
![]() $library\leftrightarrow\bot$
". Next, suppose that the conditional with an alternative antecedent: “If she has some textbooks to read then she will study late in the library" is given. The program becomes
$library\leftrightarrow\bot$
". Next, suppose that the conditional with an alternative antecedent: “If she has some textbooks to read then she will study late in the library" is given. The program becomes
Given the fact
![]() $\neg essay$
(or equivalently, the CWA rule “
$\neg essay$
(or equivalently, the CWA rule “
![]() $essay\leftarrow\bot$
"), the completed program:
$essay\leftarrow\bot$
"), the completed program:
 \begin{eqnarray*} && library\;\leftrightarrow\; (essay\wedge \neg ab_1)\vee (text\wedge \neg ab_2),\\ && ab_1\leftrightarrow\bot,\\ && ab_2\leftrightarrow\bot,\\ && essay\leftrightarrow\bot\end{eqnarray*}
\begin{eqnarray*} && library\;\leftrightarrow\; (essay\wedge \neg ab_1)\vee (text\wedge \neg ab_2),\\ && ab_1\leftrightarrow\bot,\\ && ab_2\leftrightarrow\bot,\\ && essay\leftrightarrow\bot\end{eqnarray*}
does not derive “
![]() $library\leftrightarrow\bot$
". Thus, the DA inference is suppressed. They also characterize Byrne’s suppression of valid inference. Suppose the conditional with an additional antecedent: “If the library stays open then she will study late in the library." The program becomes
$library\leftrightarrow\bot$
". Thus, the DA inference is suppressed. They also characterize Byrne’s suppression of valid inference. Suppose the conditional with an additional antecedent: “If the library stays open then she will study late in the library." The program becomes
They also introduce interaction of abnormality atoms as
Completing these four rules with “
![]() $ab_1\leftarrow \bot$
" and “
$ab_1\leftarrow \bot$
" and “
![]() $ab_3\leftarrow\bot$
" produces
$ab_3\leftarrow\bot$
" produces
 \begin{eqnarray*}&& library\leftrightarrow (essay\wedge \neg ab_1)\vee (open\wedge \neg ab_3), \\&& ab_1\leftrightarrow \neg open\vee\bot,\\&& ab_3\leftrightarrow \neg essay\vee\bot,\end{eqnarray*}
\begin{eqnarray*}&& library\leftrightarrow (essay\wedge \neg ab_1)\vee (open\wedge \neg ab_3), \\&& ab_1\leftrightarrow \neg open\vee\bot,\\&& ab_3\leftrightarrow \neg essay\vee\bot,\end{eqnarray*}
which reduces to
Then, essay alone does not deduce library, so the AA inference is suppressed. Stenning and Lambalgen (2008) argue that most people represent the effect of an additional premise formally as “
![]() $p\leftarrow q\wedge r$
" and that of an alternative premise formally as “
$p\leftarrow q\wedge r$
" and that of an alternative premise formally as “
![]() $p\leftarrow q\vee r$
." This argument coincides with our view addressed in Section 5.1.
$p\leftarrow q\vee r$
." This argument coincides with our view addressed in Section 5.1.
Dietz et al. (Reference Dietz, Hölldobler and Ragni2012) point out a technical flaw in the formulation by Stenning and Lambalgen (2008). In the above example, open and library are unknown ( U) under the 3-valued logic, then the rule “
![]() $library\,\leftarrow\, open\wedge \neg ab_3$
" becomes “
$library\,\leftarrow\, open\wedge \neg ab_3$
" becomes “
![]() ${\sf U}\leftarrow {\sf U.}$
" Under the Fitting semantics, however, the truth value of the rule “
${\sf U}\leftarrow {\sf U.}$
" Under the Fitting semantics, however, the truth value of the rule “
![]() ${\sf U}\leftarrow {\sf U}$
" is
${\sf U}\leftarrow {\sf U}$
" is
![]() ${\sf U}$
, then it does not represent the truth of the rule “
${\sf U}$
, then it does not represent the truth of the rule “
![]() $library\,\leftarrow\, open\wedge \neg ab_3$
." To remedy the problem, they employ Łukasiewicz’s 3-valued logic which maps “
$library\,\leftarrow\, open\wedge \neg ab_3$
." To remedy the problem, they employ Łukasiewicz’s 3-valued logic which maps “
![]() ${\sf U}\leftarrow {\sf U}$
" to
${\sf U}\leftarrow {\sf U}$
" to
![]() $\top$
. Dietz et al. (Reference Dietz, Hölldobler and Ragni2012) also characterize the suppression effects in AC or DC using an abductive logic program
$\top$
. Dietz et al. (Reference Dietz, Hölldobler and Ragni2012) also characterize the suppression effects in AC or DC using an abductive logic program
![]() $\langle\,\Pi, \Gamma\,\rangle$
with abducibles
$\langle\,\Pi, \Gamma\,\rangle$
with abducibles
![]() $\Gamma=\{\, p\leftarrow\bot,\;\; p\leftarrow\top\,\}$
. Consider
$\Gamma=\{\, p\leftarrow\bot,\;\; p\leftarrow\top\,\}$
. Consider
![]() $\langle\,\Pi_1, \Gamma_1\,\rangle$
where
$\langle\,\Pi_1, \Gamma_1\,\rangle$
where
 \begin{eqnarray*}\Pi_1:&& library\leftarrow essay\wedge \neg ab_1,\\&& ab_1\leftarrow\bot,\\\Gamma_1:&& essay\leftarrow\bot,\;\;\; essay\leftarrow\top,\end{eqnarray*}
\begin{eqnarray*}\Pi_1:&& library\leftarrow essay\wedge \neg ab_1,\\&& ab_1\leftarrow\bot,\\\Gamma_1:&& essay\leftarrow\bot,\;\;\; essay\leftarrow\top,\end{eqnarray*}
the weakly completed program of
![]() $\Pi_1$
becomes
$\Pi_1$
becomes
The observation
![]() $O=(library\leftrightarrow\top)$
derives “
$O=(library\leftrightarrow\top)$
derives “
![]() $essay\leftrightarrow\top$
," then “
$essay\leftrightarrow\top$
," then “
![]() $essay\leftarrow\top$
" is the skeptical explanation of O. When the additional rules and abducibles
$essay\leftarrow\top$
" is the skeptical explanation of O. When the additional rules and abducibles
 \begin{eqnarray*}\Pi_2: && library\leftarrow text\wedge \neg ab_2,\\&& ab_2\leftarrow\bot,\\\Gamma_2: && text\leftarrow\bot,\;\;\; text\leftarrow\top\end{eqnarray*}
\begin{eqnarray*}\Pi_2: && library\leftarrow text\wedge \neg ab_2,\\&& ab_2\leftarrow\bot,\\\Gamma_2: && text\leftarrow\bot,\;\;\; text\leftarrow\top\end{eqnarray*}
are given, the weakly completed program of
![]() $\Pi_1\cup\Pi_2$
becomes
$\Pi_1\cup\Pi_2$
becomes
 \begin{eqnarray*} && library\leftrightarrow (essay\wedge \neg ab_1)\vee (text\wedge\neg ab_2),\\ && ab_1\leftrightarrow\bot,\\ && ab_2\leftrightarrow\bot.\end{eqnarray*}
\begin{eqnarray*} && library\leftrightarrow (essay\wedge \neg ab_1)\vee (text\wedge\neg ab_2),\\ && ab_1\leftrightarrow\bot,\\ && ab_2\leftrightarrow\bot.\end{eqnarray*}
The observation
![]() $O=(library\leftrightarrow\top)$
derives “
$O=(library\leftrightarrow\top)$
derives “
![]() $essay\vee text\leftrightarrow\top,$
" and there are two credulous explanations “
$essay\vee text\leftrightarrow\top,$
" and there are two credulous explanations “
![]() $essay\leftarrow\top$
" and “
$essay\leftarrow\top$
" and “
![]() $text\leftarrow\top$
" in
$text\leftarrow\top$
" in
![]() $\Gamma_1\cup\Gamma_2$
. In this case, “
$\Gamma_1\cup\Gamma_2$
. In this case, “
![]() $essay\leftarrow\top$
" is not concluded under skeptical reasoning, which represents the suppression of AC.
$essay\leftarrow\top$
" is not concluded under skeptical reasoning, which represents the suppression of AC.
Comparing the above mentioned two studies with our approach, there are several differences. First, they translate a conditional sentence “if p then q" into the rule “
![]() $q\leftarrow p\wedge \neg\,ab.$
" However, it is unlikely that people who commit logical fallacies, especially younger children (Rumain et al. Reference Rumain, Connell and Braine1983), translate the conditional sentence into the rule of the above complex form in their mind. We represent the conditional sentence directly as “
$q\leftarrow p\wedge \neg\,ab.$
" However, it is unlikely that people who commit logical fallacies, especially younger children (Rumain et al. Reference Rumain, Connell and Braine1983), translate the conditional sentence into the rule of the above complex form in their mind. We represent the conditional sentence directly as “
![]() $q\leftarrow p$
" and assume that people would interpret it as bi-conditional depending on the context in which it is used. Second, in order to characterize AC or DC reasoning, Stenning and Lambalgen (2008) interpret a conditional sentence as an integrity constraint, while Dietz et al. (Reference Dietz, Hölldobler and Ragni2012) use abductive logic programs. Our framework does not need a specific interpretation of rules (such as integrity constraints) nor need an extra mechanism of abductive logic programs. Third, they use a single (weak) completion for all AC/DA/DC reasoning, while we introduce different types of completions for each inference. By separating respective completions, individual inferences are realized in a modular way and freely combined depending on their application context. For instance, we use AC and (S)DA completion to characterize the suppression task (Section 5.1), while use AC and (W)DC completion to characterize Wason selection task (Section 5.2). Fourth, they handle normal logic programs, while our framework can handle a more general class of logic programs containing disjunction and two different types of negation. For instance, consider the rule: “
$q\leftarrow p$
" and assume that people would interpret it as bi-conditional depending on the context in which it is used. Second, in order to characterize AC or DC reasoning, Stenning and Lambalgen (2008) interpret a conditional sentence as an integrity constraint, while Dietz et al. (Reference Dietz, Hölldobler and Ragni2012) use abductive logic programs. Our framework does not need a specific interpretation of rules (such as integrity constraints) nor need an extra mechanism of abductive logic programs. Third, they use a single (weak) completion for all AC/DA/DC reasoning, while we introduce different types of completions for each inference. By separating respective completions, individual inferences are realized in a modular way and freely combined depending on their application context. For instance, we use AC and (S)DA completion to characterize the suppression task (Section 5.1), while use AC and (W)DC completion to characterize Wason selection task (Section 5.2). Fourth, they handle normal logic programs, while our framework can handle a more general class of logic programs containing disjunction and two different types of negation. For instance, consider the rule: “
![]() $buy\_car \,;\, buy\_house \leftarrow win\_lottery$
" (if she wins the lottery, she buys a car or a house). When it is known that
$buy\_car \,;\, buy\_house \leftarrow win\_lottery$
" (if she wins the lottery, she buys a car or a house). When it is known that
![]() $buy\_car$
is true, one may infer
$buy\_car$
is true, one may infer
![]() $win\_lottery$
by AC inference. The AC completion realizes such an inference by introducing rules: “
$win\_lottery$
by AC inference. The AC completion realizes such an inference by introducing rules: “
![]() $win\_lottery\leftarrow buy\_car$
" and “
$win\_lottery\leftarrow buy\_car$
" and “
![]() $win\_lottery\leftarrow buy\_house.$
"
$win\_lottery\leftarrow buy\_house.$
"
Cramer et al. (Reference Cramer, Hölldobler and Ragnl2021) represent conditionals as in Stenning and Lambalgen (2008) and use the weak completion and abductive logic programs as in Dietz et al. (Reference Dietz, Hölldobler and Ragni2012). They formulate different types of conditionals based on their contexts and argue in which case AC or DC is more likely to happen. More precisely, a conditional sentence whose consequent appears to be obligatory given the antecedent is called an obligation conditional. An example of an obligation conditional is that “ if Paul rides a motorbike, then he must wear a helmet." If the consequence of a conditional is not obligatory, then it is called a factual conditional. The antecedent A of a conditional sentence is said to be necessary iff its consequent C cannot be true unless A is true. For example, the library’s being open is a necessary antecedent for studying in the library. Cramer
![]() $et\,al.$
argue that AA and DA occur independently of the type of a conditional. On the other hand, in AC most people will conclude A from “
$et\,al.$
argue that AA and DA occur independently of the type of a conditional. On the other hand, in AC most people will conclude A from “
![]() $A\Rightarrow C$
" and C, while the number of people who conclude nothing will increase if A is a non-necessary antecedent. In DC, most people will conclude
$A\Rightarrow C$
" and C, while the number of people who conclude nothing will increase if A is a non-necessary antecedent. In DC, most people will conclude
![]() $\neg\,A$
from “
$\neg\,A$
from “
![]() $A\Rightarrow C$
" and
$A\Rightarrow C$
" and
![]() $\neg\,C$
, while the number of people who conclude nothing will increase if the conditional is factual. Those assumptions are verified by questioning participants who do not receive any education in logic beyond high school training. They then formulate the situation by introducing the abducible “
$\neg\,C$
, while the number of people who conclude nothing will increase if the conditional is factual. Those assumptions are verified by questioning participants who do not receive any education in logic beyond high school training. They then formulate the situation by introducing the abducible “
![]() $C\leftarrow\top$
" if the antecedent is non-necessary, and “
$C\leftarrow\top$
" if the antecedent is non-necessary, and “
![]() $ab\leftarrow\top$
" if the conditional is factual. In the former case, the observation C does not imply A because the additional “
$ab\leftarrow\top$
" if the conditional is factual. In the former case, the observation C does not imply A because the additional “
![]() $C\leftarrow\top$
" can make C explainable by itself. As a result, A is not a skeptical explanation of C. In the latter case, the observation
$C\leftarrow\top$
" can make C explainable by itself. As a result, A is not a skeptical explanation of C. In the latter case, the observation
![]() $\neg\, C$
does not imply
$\neg\, C$
does not imply
![]() $\neg\, A$
because if one employs the explanation “
$\neg\, A$
because if one employs the explanation “
![]() $ab\leftarrow\top$
" then “
$ab\leftarrow\top$
" then “
![]() $C\leftarrow A\wedge \neg ab$
" does not produce “
$C\leftarrow A\wedge \neg ab$
" does not produce “
![]() $C\leftrightarrow A$
."
$C\leftrightarrow A$
."
Dietz et al. (Reference Dietz, Fichte and Hamiti2022) use logic programming rules to represent different types of conditionals. For instance,
represents MP that
![]() ${\sf concl}$
follows if a sufficient premise is asserted to be true. By contrast,
${\sf concl}$
follows if a sufficient premise is asserted to be true. By contrast,
represents DA that
![]() ${\sf concl}$
does not follow if a necessary premise is asserted to be false. With these rules, Byrne’s suppression effect is represented as follows. First, given the fact
${\sf concl}$
does not follow if a necessary premise is asserted to be false. With these rules, Byrne’s suppression effect is represented as follows. First, given the fact
![]() ${\sf prem(essay)}$
and
${\sf prem(essay)}$
and
![]() ${\sf sufficient(essay)}$
,
${\sf sufficient(essay)}$
,
implies
![]() ${\sf library}$
. Next, given the additional fact
${\sf library}$
. Next, given the additional fact
![]() ${\sf necessary(open)}$
and in the absence of
${\sf necessary(open)}$
and in the absence of
![]() ${\sf prem(open)}$
${\sf prem(open)}$
has the effect of withdrawing
![]() ${\sf library}$
. In the current study, we do not distinguish different types of conditionals as in Cramer et al. (Reference Cramer, Hölldobler and Ragnl2021) and Dietz et al. (Reference Dietz, Fichte and Hamiti2022). However, completion is done for individual rules, so we could realize partial completion by selecting rules
${\sf library}$
. In the current study, we do not distinguish different types of conditionals as in Cramer et al. (Reference Cramer, Hölldobler and Ragnl2021) and Dietz et al. (Reference Dietz, Fichte and Hamiti2022). However, completion is done for individual rules, so we could realize partial completion by selecting rules
![]() $\Pi'\subseteq \Pi$
that are subject to be completed in practice. More precisely, if a program
$\Pi'\subseteq \Pi$
that are subject to be completed in practice. More precisely, if a program
![]() $\Pi$
consists of rules
$\Pi$
consists of rules
![]() $R_1$
having necessary antecedents and
$R_1$
having necessary antecedents and
![]() $R_2$
having non-necessary antecedents, apply AC completion to
$R_2$
having non-necessary antecedents, apply AC completion to
![]() $R_1$
while keep
$R_1$
while keep
![]() $R_2$
as they are. The resulting program then realizes AC inference using
$R_2$
as they are. The resulting program then realizes AC inference using
![]() $R_1$
only. Likewise, if a program
$R_1$
only. Likewise, if a program
![]() $\Pi$
consists of rules
$\Pi$
consists of rules
![]() $R_3$
having obligatory consequents and
$R_3$
having obligatory consequents and
![]() $R_4$
having factual consequents, apply DC completion to
$R_4$
having factual consequents, apply DC completion to
![]() $R_3$
while keep
$R_3$
while keep
![]() $R_4$
as they are. The resulting program then realizes DC inference using
$R_4$
as they are. The resulting program then realizes DC inference using
![]() $R_3$
only. Such a partial completion is also effectively used for commonsense reasoning in this paper (Proposition 6.2(ii), Definition 6.3).
$R_3$
only. Such a partial completion is also effectively used for commonsense reasoning in this paper (Proposition 6.2(ii), Definition 6.3).
7.3 Commonsense reasoning
Console et al. (Reference Console, Dupré and Torasso1991) and Fung and Kowalski (Reference Fung and Kowalski1997) compute abduction by deduction using Clark completion. Abduction using AC and DC completion is close to those approaches, while the approach based on Clark completion is restricted to normal logic programs (NLPs). We argued that a (positive) observation
![]() $O=\neg G$
is distinguished from a negative observation
$O=\neg G$
is distinguished from a negative observation
![]() $O=not\,G$
, but such a distinction is not considered in NLPs handling only default negation. Inoue and Sakama (Reference Inoue and Sakama1999) introduce transaction programs to compute extended abduction. Extended abduction computes explanations for not only (positive) observations but also negative ones. A transaction program is constructed based on the converse of conditionals, and its semantics is operationally given as a fixpoint of the program. A transaction program is a meta-level specification of the procedure and is different from the current approach. Moreover, a transaction program is defined for NLPs only.
$O=not\,G$
, but such a distinction is not considered in NLPs handling only default negation. Inoue and Sakama (Reference Inoue and Sakama1999) introduce transaction programs to compute extended abduction. Extended abduction computes explanations for not only (positive) observations but also negative ones. A transaction program is constructed based on the converse of conditionals, and its semantics is operationally given as a fixpoint of the program. A transaction program is a meta-level specification of the procedure and is different from the current approach. Moreover, a transaction program is defined for NLPs only.
Pereira et al. (Reference Pereira, Aparício and Alferes1991, 2017) realize counterfactual reasoning in logic programming. In Pereira et al. (Reference Pereira, Aparício and Alferes1991), a counterfactual conditional “
![]() ${\varphi} >\psi$
" (meaning
${\varphi} >\psi$
" (meaning
![]() ${\varphi}\,\Box\!\!\!\rightarrow\,\psi$
) is evaluated in a program
${\varphi}\,\Box\!\!\!\rightarrow\,\psi$
) is evaluated in a program
![]() $\Pi$
by adding
$\Pi$
by adding
![]() ${\varphi}$
to
${\varphi}$
to
![]() $\Pi$
and computing the maximal non-contradictory submodels of the new program. Then, the counterfactual conditional is true iff
$\Pi$
and computing the maximal non-contradictory submodels of the new program. Then, the counterfactual conditional is true iff
![]() $\psi$
holds in all such submodels. Pereira and Saptawijaya (Reference Pereira and Saptawijaya2017) first use abduction to compute possible causes of an event. Next, they assume counterfactual assumption and verify whether an expected outcome will happen under possible causes. These studies consider extended/normal logic programs under the well-founded semantics and realize counterfactual reasoning via program revision or abductive reasoning. Unlike our approach, they do not introduce new rules for DA inference in counterfactual reasoning.
$\psi$
holds in all such submodels. Pereira and Saptawijaya (Reference Pereira and Saptawijaya2017) first use abduction to compute possible causes of an event. Next, they assume counterfactual assumption and verify whether an expected outcome will happen under possible causes. These studies consider extended/normal logic programs under the well-founded semantics and realize counterfactual reasoning via program revision or abductive reasoning. Unlike our approach, they do not introduce new rules for DA inference in counterfactual reasoning.
Gaasterland et al. (Reference Gaasterland, Godfrey and Minker1992) introduce neighborhood inference for query answering in Horn logic programs. The scope of a query is expanded by relaxing the specification, which allows a program to return answers related to the original query. They introduce a meta-interpreter to realize it and argue for control strategies. We show that similar reasoning is simulated in ASP using the AC completion.
8 Conclusion
This paper studies a method of realizing human conditional reasoning in ASP. Different types of completions are introduced to realize logically invalid inferences AC and DA as well as a logically valid inference DC. They are applied to representing human reasoning tasks in the literature and are also used for computing common sense reasoning in AI. In psychology and cognitive science, empirical studies show that people perform AC, DA, or DC inference depending on the context in which a conditional sentence is used. We could import the results of those studies and encode knowledge in a way that people are likely to use it. The proposed theory is used for such a purpose to realize pragmatic inference in ASP and produce results that are close to human reasoning in practice.
Completions introduced in this paper are defined in a modular way, so one can apply respective completion to specific rules of a program according to their contexts. They are combined freely and can be mixed in the same program. Those completions are general in the sense that they are applied to logic programs containing disjunction, explicit, and default negation. Since a completed program is still in the class of GEDPs and a GEDP is transformed to a semantically equivalent EDP (Inoue and Sakama Reference Inoue and Sakama1998), answer sets of completed programs are computed using existing answer set solvers.