Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T06:17:23.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrating Cardinality Constraints into Constraint Logic Programming with Sets

Published online by Cambridge University Press:  09 November 2021

MAXIMILIANO CRISTIÁ Open the ORCID record for MAXIMILIANO CRISTIÁ [Opens in a new window]  and
GIANFRANCO ROSSI
MAXIMILIANO CRISTIÁ
Affiliation:
Universidad Nacional de Rosario and CIFASIS, Argentina (e-mail: cristia@cifasis-conicet.gov.ar)
GIANFRANCO ROSSI
Affiliation:
Università di Parma, Italy (e-mail: gianfranco.rossi@unipr.it)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Formal reasoning about finite sets and cardinality is important for many applications, including software verification, where very often one needs to reason about the size of a given data structure. The Constraint Logic Programming tool 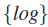$$\{ log\} $$ provides a decision procedure for deciding the satisfiability of formulas involving very general forms of finite sets, although it does not provide cardinality constraints. In this paper we adapt and integrate a decision procedure for a theory of finite sets with cardinality into 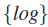$$\{ log\} $$ . The proposed solver is proved to be a decision procedure for its formulas. Besides, the new CLP instance is implemented as part of the 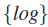$$\{ log\} $$ tool. In turn, the implementation uses Howe and King’s Prolog SAT solver and Prolog’s CLP(Q) library, as an integer linear programming solver. The empirical evaluation of this implementation based on +250 real verification conditions shows that it can be useful in practice.

Under consideration in Theory and Practice of Logic Programming (TPLP)

Keywords

{log}set theorycardinalityformal verificationconstraint logic programming
Type
Original Article
Information
Theory and Practice of Logic Programming , Volume 23 , Issue 2 , March 2023 , pp. 468 - 502
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Abrial, J.-R. 1996. The B-book: Assigning Programs to Meanings. Cambridge University Press, New York, NY, USA.Google Scholar
Alberti, F., Ghilardi, S. and Pagani, E. 2017. Cardinality constraints for arrays (decidability results and applications). Formal Methods Syst. Des. 51, 3, 545–574.Google Scholar
Azevedo, F. 2007. Cardinal: A finite sets constraint solver. Constraints 12, 1, 93–129.CrossRefGoogle Scholar
Bansal, K., Barrett, C. W., Reynolds, A. and Tinelli, C. 2018. Reasoning with finite sets and cardinality constraints in SMT. Log. Methods Comput. Sci. 14, 4.Google Scholar
Bender, M. and Sofronie-Stokkermans, V. 2017. Decision procedures for theories of sets with measures. In Automated Deduction - CADE 26 - 26th International Conference on Automated Deduction, Gothenburg, Sweden, August 6-11, 2017, Proceedings, de Moura, L., Ed. Lecture Notes in Computer Science, vol. 10395. Springer, 166–184.Google Scholar
Berkovits, I., Lazic, M., Losa, G., Padon, O. and Shoham, S. 2019. Verification of threshold-based distributed algorithms by decomposition to decidable logics. In Computer Aided Verification – 31st International Conference, CAV 2019, New York City, NY, USA, July 15-18, 2019, Proceedings, Part II, Dillig, I. and Tasiran, S., Eds. Lecture Notes in Computer Science, vol. 11562. Springer, 245–266.Google Scholar
Bradley, A. R., Manna, Z. and Sipma, H. B. 2006. What’s decidable about arrays? In Verification, Model Checking, and Abstract Interpretation, 7th International Conference, VMCAI 2006, Charleston, SC, USA, January 8–10, 2006, Proceedings, Emerson, E. A. and Namjoshi, K. S., Eds. Lecture Notes in Computer Science, vol. 3855. Springer, 427–442.Google Scholar
Cantone, D., Omodeo, E. G. and Policriti, A. 2001. Set Theory for Computing - From Decision Procedures to Declarative Programming with Sets . Monographs in Computer Science. Springer.Google Scholar
Clearsy. Atelier B home page. http://www.atelierb.eu/.Google Scholar
Cristiá, M. and Rossi, G. 2017. A decision procedure for restricted intensional sets. In Automated Deduction - CADE 26 - 26th International Conference on Automated Deduction, Gothenburg, Sweden, August 6–11, 2017, Proceedings, de Moura, L., Ed. Lecture Notes in Computer Science, vol. 10395. Springer, 185–201.Google Scholar
Cristiá, M. and Rossi, G. 2018. A set solver for finite set relation algebra. In Relational and Algebraic Methods in Computer Science - 17th International Conference, RAMiCS 2018, Groningen, The Netherlands, October 29 - November 1, 2018, Proceedings, Desharnais, J., Guttmann, W., and Joosten, S., Eds. Lecture Notes in Computer Science, vol. 11194. Springer, 333–349.Google Scholar
Cristiá, M. and Rossi, G. 2019. Rewrite rules for a solver for sets, binary relations and partial functions. Tech. rep. http://people.dmi.unipr.it/gianfranco.rossi/SETLOG/calculus.pdf.Google Scholar
Cristiá, M. and Rossi, G. 2020. Solving quantifier-free first-order constraints over finite sets and binary relations. J. Autom. Reason. 64, 2, 295–330.Google Scholar
Cristiá, M. and Rossi, G. 2021a. Automated proof of Bell-LaPadula security properties. J. Autom. Reason. 65, 4, 463–478.Google Scholar
Cristiá, M. and Rossi, G. 2021b. Automated reasoning with restricted intensional sets. J. Autom. Reason. 65, 6, 809–890.CrossRefGoogle Scholar
Cristiá, M. and Rossi, G. 2021. An automatically verified prototype of the Tokeneer ID Station specification. J. Autom. Reason. 65, 8, 1125–1151.CrossRefGoogle Scholar
Cristiá, M., Rossi, G. and Frydman, C. S. 2013. {log} as a test case generator for the Test Template Framework. In SEFM, Hierons, R. M., Merayo, M. G., and Bravetti, M., Eds. Lecture Notes in Computer Science, vol. 8137. Springer, 229–243.Google Scholar
Dal Palú, A., Dovier, A., Pontelli, E. and Rossi, G. 2003. Integrating finite domain constraints and CLP with sets. In Proceedings of the 5th ACM SIGPLAN International Conference on Principles and Practice of Declaritive Programming. PPDP ’03. ACM, New York, NY, USA, 219–229.Google Scholar
Ding, Y., Harrison-Trainor, M. and Holliday, W. H. 2020. The logic of comparative cardinality. J. Symb. Log., 1–40.Google Scholar
Dovier, A., Omodeo, E. G., Pontelli, E. and Rossi, G. 1996. A language for programming in logic with finite sets. J. Log. Program. 28, 1, 1–44.Google Scholar
Dovier, A., Piazza, C., Pontelli, E. and Rossi, G. 2000. Sets and constraint logic programming. ACM Trans. Program. Lang. Syst. 22, 5, 861–931.Google Scholar
Dovier, A., Pontelli, E. and Rossi, G. 2006. Set unification. Theory Pract. Log. Program. 6, 6, 645–701.CrossRefGoogle Scholar
Ferro, A., Omodeo, E. G. and Schwartz, J. T. 1980. Decision procedures for some fragments of set theory. In CADE, Bibel, W. and Kowalski, R. A., Eds. Lecture Notes in Computer Science, vol. 87. Springer, 88–96.Google Scholar
Gervet, C. 1994. Conjunto: Constraint propagation over set constraints with finite set domain variables. In ICLP, Hentenryck, P. V, Ed. MIT Press, 733.Google Scholar
Gervet, C. 1997. Interval propagation to reason about sets: Definition and implementation of a practical language. Constraints An Int. J. 1, 3, 191–244.CrossRefGoogle Scholar
Hawkins, P., Lagoon, V. and Stuckey, P. J. 2005. Solving set constraint satisfaction problems using ROBDDs. J. Artif. Intell. Res. (JAIR) 24, 109–156.CrossRefGoogle Scholar
Hibti, M. 1995. Décidabilité et complexité de systèmes de contraintes ensemblistes. Ph.D. thesis. Thèse de doctorat dirigée par Lombardi, Henri Sciences appliquées Besançon 1995.Google Scholar
Holzbaur, C. 1995. OFAI CLP(Q,R) manual. Tech. rep., edition 1.3.3. Technical Report TR-95-09, Austrian Research Institute for Artificial Intelligence.Google Scholar
Howe, J. M. and King, A. 2012. A pearl on SAT and SMT solving in Prolog. Theor. Comput. Sci. 435, 43–55.CrossRefGoogle Scholar
Kisby, C., Blanco, S., Kruckman, A. and Moss, L. S. 2020. Logics for sizes with union or intersection. In The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, February 7-12, 2020. AAAI Press, 2870–2876.Google Scholar
Kuncak, V., Nguyen, H. H. and Rinard, M. C. 2006. Deciding Boolean algebra with Presburger arithmetic. J. Autom. Reason. 36, 3, 213–239.Google Scholar
Leuschel, M. and Butler, M. 2003. ProB: A model checker for B. In FME, Keijiro, A., Gnesi, S., and Mandrioli, D., Eds. Lecture Notes in Computer Science, vol. 2805. Springer-Verlag, 855–874.Google Scholar
Levatich, M., Bjørner, N., Piskac, R. and Shoham, S. 2020. Solving LIA* using approximations. In Verification, Model Checking, and Abstract Interpretation – 21st International Conference, VMCAI 2020, New Orleans, LA, USA, January 16-21, 2020, Proceedings, Beyer, D. and Zufferey, D., Eds. Lecture Notes in Computer Science, vol. 11990. Springer, 360–378.Google Scholar
Piskac, R. 2020. Efficient automated reasoning about sets and multisets with cardinality constraints. In Automated Reasoning – 10th International Joint Conference, IJCAR 2020, Paris, France, July 1-4, 2020, Proceedings, Part I, Peltier, N. and Sofronie-Stokkermans, V., Eds. Lecture Notes in Computer Science, vol. 12166. Springer, 3–10.Google Scholar
Piskac, R. and Kuncak, V. 2008. Decision procedures for multisets with cardinality constraints. In Verification, Model Checking, and Abstract Interpretation, 9th International Conference, VMCAI 2008, San Francisco, USA, January 7–9, 2008, Proceedings, Logozzo, F., Peled, D. A., and Zuck, L. D., Eds. Lecture Notes in Computer Science, vol. 4905. Springer, 218–232.Google Scholar
Piskac, R. and Kuncak, V. 2010. MUNCH – Automated reasoner for sets and multisets. In Automated Reasoning, 5th International Joint Conference, IJCAR 2010, Edinburgh, UK, July 16–19, 2010. Proceedings, Giesl, J. and Hähnle, R., Eds. Lecture Notes in Computer Science, vol. 6173. Springer, 149–155.Google Scholar
Rossi, G. 2008. $$\{ log\} $$ . http://people.dmi.unipr.it/gianfranco.rossi/setlog.Home.html. Last access 2021.Google Scholar
Saaltink, M. 1997. The Z/EVES system. In ZUM, Bowen, J. P., Hinchey, M. G., and Till, D., Eds. Lecture Notes in Computer Science, vol. 1212. Springer, 72–85.Google Scholar
Spivey, J. M. 1992. The Z Notation: A Reference Manual. Prentice Hall International (UK) Ltd., Hertfordshire, UK, UK.Google Scholar
Stuckey, P. J., Marriott, K. and Tack, G. 2020. The MiniZinc Handbook. Tech. rep. https://www.minizinc.org/doc-2.5.3/en/index.html.Google Scholar
Stump, A., Barrett, C. W., Dill, D. L. and Levitt, J. R. 2001. A decision procedure for an extensional theory of arrays. In 16th Annual IEEE Symposium on Logic in Computer Science, Boston, Massachusetts, USA, June 16-19, 2001, Proceedings. IEEE Computer Society, 29–37.Google Scholar
Suter, P., Steiger, R. and Kuncak, V. 2011. Sets with cardinality constraints in satisfiability modulo theories. In Verification, Model Checking, and Abstract Interpretation - 12th International Conference, VMCAI 2011, Austin, TX, USA, January 23-25, 2011. Proceedings, Jhala, R. and Schmidt, D. A., Eds. Lecture Notes in Computer Science, vol. 6538. Springer, 403–418.Google Scholar
Williams, H. P. 2009. Logic and Integer Programming, 1st ed. Springer Publishing Company, Incorporated.CrossRefGoogle Scholar
Yessenov, K., Piskac, R. and Kuncak, V. 2010. Collections, cardinalities, and relations. In Verification, Model Checking, and Abstract Interpretation, 11th International Conference, VMCAI 2010, Madrid, Spain, January 17–19, 2010. Proceedings, Barthe, G. and Hermenegildo, M. V., Eds. Lecture Notes in Computer Science, vol. 5944. Springer, 380–395.Google Scholar
Zarba, C. G. 2002a. Combining multisets with integers. In Automated Deduction - CADE-18, 18th International Conference on Automated Deduction, Copenhagen, Denmark, July 27-30, 2002, Proceedings, Voronkov, A, Ed. Lecture Notes in Computer Science, vol. 2392. Springer, 363–376.Google Scholar
Zarba, C. G. 2002b. Combining sets with integers. In Frontiers of Combining Systems, 4th International Workshop, FroCoS 2002, Santa Margherita Ligure, Italy, April 8-10, 2002, Proceedings, Armando, A, Ed. Lecture Notes in Computer Science, vol. 2309. Springer, 103–116.Google Scholar
Zarba, C. G. 2005. Combining sets with cardinals. J. Autom. Reason. 34, 1, 1–29.CrossRefGoogle Scholar